A fizika története

| „ | Ha távolabbra láttam másoknál, azt azért tehettem, mert óriások vállán álltam. | ” |
| – Isaac Newton[1] | ||
A fizika (az ógörög φύσις physis szóból, jelentése „természet”) a tudomány egyik alapvető ága. Vizsgálatának elsődleges tárgya az anyag és az energia. A fizika bizonyos felfogásban a legrégebbi és legalapvetőbb akadémiai tevékenység, felfedezései gyakran a természettudományokon keresztül találnak alkalmazást, hiszen az anyag és az energia a természeti világ alapvető jelenségei. Más tudományokra általában jellemző, hogy témakörük a fizikáéhoz képest korlátozottabb. Egyes tudományterületek önálló tudományággá válásuk előtt az általános fizikai tudományok témakörébe estek. Ma a fizika leegyszerűsítve klasszikus fizikára és modern fizikára bontható.
Ókori története[szerkesztés]
A ma ismert fizika alapvető elemei elsődlegesen a csillagászat, a fénytan és a mechanika területéről származnak, melyeket az ókorban a geometria tanulmányozása hajtotta. Ezen területek matematikai eszköztára az ókori babilóniaiaknak és a hellenizmus egyes tudósainak köszönhetők, többek között Arkhimédész és Ptolemaiosz munkájának. Az ókori filozófia – beleértve azt, amit ezen belül fizikának hívtak – emellett a természet olyan elvont ideákon keresztüli magyarázatára összpontosított, mint Arisztotelész négyfajta okozata.
Ókori Görögország[szerkesztés]

A természet racionális megértése felé történő elmozdulás kezdete Görögországban a preszókratikus filozófusokkal a poliszok korára (i. e. 650–480) tehető. A filozófus Thalész (i. e. 7. és 6. század) elutasította a természeti jelenségek különböző természetfeletti, vallási és mitológiai magyarázatainak elfogadását, azt hirdette, hogy minden eseménynek természeti oka van. Ezen vélekedés miatt nevezik őt a „tudomány atyjának”.[2] Thalész több fontos eredménye járult hozzá a fizika fejlődéséhez. I. e. 580-ban a vizet javasolta alapelemnek (görögül: őselem, arche), kísérletezett a mágnesek és a megdörzsölt borostyán közti vonzással, és kialakította az első fennmaradt, tudományos igényű kozmológiai rendszert.
Anaximandrosz, aki az ős-evolúciós elméletéről híres, vitatta Thalész elképzeléseit az ősanyagra vonatkozóan: víz helyett az apeiron nevű összetevőt javasolta minden anyag építőkövének. I. e. 500 körül az Epheszoszi Hérakleitosz azt javasolta, hogy a világegyetemet uraló egyetlen alapvető törvény a változás elve legyen, mely szerint semmi sem maradhat meg ugyanabban az állapotában a végtelenségig. Ezen megfigyelése miatt tekintjük őt az ókori fizikusok közt az elsőnek, aki foglalkozott az idő szerepével a világegyetemben. Ez az elgondolás és az idő természete napjaink fizikájának is kulcsfontosságú témája.[forrás?] Leukipposz az i. e. 5. század első felében felszólalt az ellen, hogy a világegyetem sorsát alapvetően közvetlen isteni beavatkozás formálja. Nézete szerint a természeti jelenségeknek valójában természeti okuk van. Leukipposz és tanítványa, Démokritosz voltak az elsők, akik kidolgozták a görög atomizmus elméletét. Ennek fontos gondolata, hogy minden anyagi tárgy teljes egészében atomokból épül fel, mely atomok elpusztíthatatlan, oszthatatlan anyagi alapegységek, elemek.
Görögországban a klasszikus (i. e. 6–4. század) és a hellenisztikus korban a természetfilozófia fejlődése következtében a fizika újszerű tudományterülete élénk tudományos érdeklődés középpontjába került. Platón egyik tanítványa, Arisztotelész (i. e. 384–322) azt az elképzelést hirdette, hogy a fizikai jelenségek megfigyelése végső soron az őket irányító természeti törvények felfedezéséhez vezethet.[forrás?] Ez egyfajta empirikus felfogás, mely ma is fontos része a fizikai modellalkotás folyamatának. Arisztotelész szerteágazó tudományos írásai többek között fizikával, metafizikával, költészettel, színházzal, zenével, logikával, retorikával, nyelvészettel, politikával, kormányzással, etikával, biológiával és állattannal kapcsolatosak. A 4. században ő írta az első könyvet, ami a vizsgálat eme tárgyára fizikaként hivatkozik: ezt tekinthetjük az ún. arisztotelészi fizikai rendszer kiindulópontjának. Munkáiban a négy elem elméletével magyarázta az olyan fizikai jelenségeket, mint a mozgás és a gravitáció. Hite szerint minden anyag az éterből áll, vagy a négy elem: a föld, a víz, a levegő és a tűz valamiféle kombinációjából. Elképzelése szerint ez a négy földi elem képes az egymás közti átalakulásra, melynek mozgatóereje az, hogy ezek az elemek „természetes helyük” felé haladjanak. Így például a kő esése afelé hat, hogy az anyagát képező föld a világegyetem középpontja felé közeledhessen, míg például a tűz lobogása felfelé, a világ pereme felé törekszik. Az arisztotelészi fizika rendkívül népszerű lett a középkori Európában, áthatva évszázadok tudományos felfogását. Az elképzelések tényleges felülvizsgálata egészen Galileo Galilei és Isaac Newton koráig váratott magára.
Már a korai klasszikus Görögországban általános volt az a nézet, hogy a Föld gömb alakú. Eratoszthenész Pentatlosz (i. e. 276–194) egy i. e. 240 körül végzett úttörő kísérletében megbecsülte bolygónk kerületét. Mivel a kerületet stadionokban adta meg, mérésének pontossága ma nehezen értelmezhető, de 10-15%-ra tehető, mely korának lehetőségeit ismerve nagyszerű szellemi teljesítménynek nevezhető.[3] Arisztotelész geocentrikus nézetével szemben a Szamoszi Arisztarkhosz (i. e. 310 k. – i. e. 230 k.) határozott érvet mutatott fel a Naprendszer heliocentrikus modelljére, azaz a Napot helyezte a rendszer közepébe a Föld helyett. Arisztarkhosz heliocentrikus elméletének egyik követője, Szeleukiai Szeleukusz azt állította, hogy a Föld a saját tengelye körül forog, amely tengely viszont a Nap körül kering. Habár érvelésének részleteit nem ismerjük, Plutarkhosz állítása nyomán Szeleukuszt tartják az elsőnek, aki a heliocentrikus rendszert magyarázattal bizonyította.

Az i. e. 3. században szürakuszai Arkhimédész (görögül: Ἀρχιμήδης (i. e. 287–212) görög matematikus lefektette az hidrosztatika, illetve a statika alapjait és leírta az emelő, mint egyszerű gép matematikai megfogalmazásának elvét. Kifejlesztett egy kifinomult csigarendszert is, amivel nagy tárgyakat lehetett mozgatni minimális erőkifejtéssel. Létrehozott egy vízemelő csavart, mely a ma is használt hidrológiai szemléletet tükrözte. Az általa kifejlesztett harci gép segítette távol tartani a Rómaiak seregeit az első pun háború idején. I. e. 250 körül írott Az úszó testekről című munkájában Arkhimédész leírta a felhajtóerő törvényét, melyet ma Arkhimédész törvénye néven is ismerünk és alkalmazunk. Arkhimédész vitatta Arisztotelész metafizikai érveit. Matematikai elvre épülő találmányaival rámutatott, hogy nem lehet szétválasztani a matematikát és a természeti törvényeket. De nem állt meg a matematika alkalmazásánál, utóbbiban is maradandót alkotott: egy parabolagörbe alatti területet sokszögesítéssel és végtelen sorösszeg kiszámolásával számolta ki, igen jó közelítést adott a pí értékére, megalkotta a nevét is viselő spirálgörbét, meghatározta a forgástestek térfogatának képletét, és alkotott egy elmés rendszert a nagyon nagy számok kifejezésére. Szintén ő fogalmazta meg a mechanikában az egyensúlyi állapot és a tömegközéppont koncepcióját, melyek később Galilei és Newton munkájára is nagy hatással voltak.
Hipparkhosz (i. e. 190–210) a csillagászatra és a matematikára összpontosított. Kifinomult geometriai okfejtéssel magyarázta a csillagok és a bolygók mozgását, illetve sikeresen jósolta meg napfogyatkozások idejét. Ezen kívül megfigyeléseket és számításokat végzett a Nap és a Hold Földtől való távolságának meghatározására. Ehhez sikerrel javított az akkor használt csillagászati eszközök pontosságán.
Klaudiosz Ptolemaiosz (i. sz. 90–168) korának híres fizikusa és egyik vezető gondolkodója volt a Római Birodalomban. Számos tudományos értekezés szerzője volt, melyek közül legalább három a későbbiekben fontos viszonyítási ponttá vált az iszlám és európai tudomány számára. Az első a manapság Almagest (görögül, Ἡ Μεγάλη Σύνταξις, „A nagy értekezés”, eredetileg Μαθηματικὴ Σύνταξις, „Matematikai értekezés”) néven ismert csillagászati értekezés. A második a Geográfia, amely a görög-római világ földrajzi tudásának alapos leírása.
Az ókori világ legtöbb összegyűjtött tudása elveszett. Még az ismertebb gondolkodók műveiből is csak pár töredék maradt fenn. Bár legalább tizennégy könyvet írt, szinte semmi sem maradt fenn Hipparkhosz közvetlen munkáiból. Az arisztoteliánusok állítólagos 150 munkáiból csak 30 van meg, és ezek közül is egyesek „nem sokkal többek, mint előadásjegyzetek”.
India és Kína[szerkesztés]
Európa mellett az ókori Kína és India is gazdag fizikai és matematikai hagyományokkal büszkélkedhet.
Az indiai filozófiában Maharishi Kanada volt az első, aki i. e. 200 körül az atomizmus elméletéhez hasonló rendszert alkotott,[4] bár egyes szerzők őt egy korábbi korszakba, az i. e. 6. századba helyezték.[5] Az ő munkájára alapozták később az elképzeléseiket a buddhista atomisták, például Dharmakírti és Dignága.[6]

Pakudha Kaccsájana i. e. 6. századi indiai filozófus és kortársa, Gautama Sziddhártha szintén atomokból álló anyagi világról értekeztek. Vélekedésük szerint az éteren kívül a többi elem fizikailag érzékelhető, ezért ezek az anyag apró részecskéiből állnak. A legapróbb ilyen anyagi részecskéket, melyeket már nem lehet tovább osztani, Parmanunak nevezték, melyet elpusztíthatatlannak, örökkévalónak tekintettek. A buddhisták az atomot a puszta szemmel nem látható parányi objektumoknak gondolták, amelyek egy pillanat alatt keletkeznek és tűnnek el. A Vaisheshika-iskola filozófusai vélekedése szerint az atom egy puszta pont a térben. Szintén ez az iskola írta le először a mozgás és a ható erő közti kapcsolatot. Az atomról szóló indiai elméletek általában elvontak és filozófiával átszőttek, mivel a logikán alapulnak és nem személyes tapasztaláson vagy kísérleteken. Az indiai csillagászatban Árjabhata Árjabhatíja (i. sz. 499) című munkájában kifejtette a Föld forgásáról szóló elképzelését. Nilakantha Somayaji, a keralai csillagászati és matematikai iskola képviselője a Tycho-féle rendszerre hasonlító fél-heliocentrikus modellt javasolt.
Az ókori Kínában a mágnesség tanulmányozása az i. e. 4. századra vezethető vissza (lásd az Ördög-völgy urának könyvében).[7] Ehhez a területhez a kínai tudósok közül a polihisztor államférfi, Shen Kuo (1031-1095) járult hozzá a legtöbbet. Ő írta le először a navigációhoz használt mágnestűs iránytű működését, és kialakította a valódi észak koncepcióját. A fénytanban Shen Kuo önállóan kifejlesztette a camera obscurát.[8]
Iszlám világ[szerkesztés]

(965 k.–1040 k.)
A 7–15. században tudományos fejlődés ment végbe a muzulmán világban. Sok klasszikus Indiai, Asszíriai, szászánida (perzsa) és görög mű arab nyelvű fordítása készült el, Arisztotelész műveivel együtt.[9] Az Avicennaként ismert Ibn Szína (980–1037) buharai (napjainkban Üzbegisztán) polihisztor több fontos eredményt tudott felmutatni a fizika, az optika, a filozófia és az orvoslás területén. Az orvostudomány kánonja című írása a legjelentősebb, melyet Európában egészen az 1600-as évekig használtak az orvostanhallgatók oktatásában.
Kimagaslóak Ibn al-Haytham (latinosan Alhazen, 965–1040) arab tudós eredményei, akit a modern optika egyik alapítójának tekintenek. Ptolemaiosz és Arisztotelész úgy elmélkedtek, hogy a fény vagy a szemből sugárzik, megvilágítva a tárgyakat, vagy magukból a testekből árad és ér el e szemig. Ezzel szemben al-Haytham úgy vélte, hogy a fény a szembe a tárgy különböző pontjairól visszaverődés után sugarak formájában érkezik. Ibn al-Haytham és Abu Rajhan Biruni perzsa tudós művei Nyugat-Európába is eljutottak, ahol olyan tanítók tanulmányozták őket, mint Roger Bacon és Witelo.[10][m 1]
Omar Hajjám (1048–1131) perzsa tudós kiszámolta a szoláris év hosszát és csak a másodperc töredékével tévedett a modern kori számításokhoz képest. Ezt a nagyszerű eredményt egy olyan naptár kidolgozására használta, mely a jó 500 évvel később kialakított Gergely-naptárnál is pontosabb volt. Őt tartják világ első tudományos ismeretterjesztőjének: egy történet szerint egy alkalommal egy szúfi teológust is meggyőzött arról, hogy a világ a tengelye körül forog.[forrás?]

A Bagdadban elhunyt Naszír ad-Dín Túszí (1201–1274) perzsa csillagász és matematikus írta a Csillagászat kincsét, mely a bolygómozgások figyelemreméltóan pontos táblázatát tartalmazta. Ez a munka megreformálta Ptolemaiosz római csillagász létező bolygómodelljét. Elképzelése az volt, hogy az összes bolygó saját pályáján egyenletes körmozgást végez. Ez a mű vezetett el később ahhoz a felfedezéshez, hogy a bolygóknak tulajdonképpen elliptikus pályájuk van. Kopernikusz később sokat épített ad-Dín Túszí és tanítványai munkásságára.[11] A ptolemaioszi rendszertől való fokozatos eltávolodás megnyitotta az utat a heliocentrikus világkép kialakulása előtt, azaz hogy a Föld kering a Nap körül.
Középkori Európa[szerkesztés]
Egyes ókori művek a középkori Európa gondolkodóihoz arab közvetítéssel juthattak csak el. Ezen ismeretek újbóli felfedezése kombinálva a judeo-iszlám teológiai kommentárokkal nagy hatással volt a középkori filozófusokra, például Aquinói Szent Tamásra. A skolasztika európai tanítói, akik az ókori klasszikus filozófusok elképzeléseit próbálták összeegyeztetni a keresztény teológiával, Arisztotelészt az ókori világ legnagyobb gondolkodójának hirdették. Azokban a dolgokban, ahol közvetlenül nem mondott ellent a Bibliának, az arisztotelészi fizika lett az európai egyházak fizikai magyarázatának alapja. A középkori Európa fizika alapvető elemévé vált az elméletek számszerűsítése.[12]
Az arisztotelészi fizikára alapozva a skolasztikus fizika elgondolása az volt, hogy a világ dolgai természetüknél fogva állandó mozgásban, változásban vannak. Az égitestek pályáját körpályának képzelték: az égi szférákra vonatkozólag azzal az előfeltételezéssel éltek, hogy ott fent csakis a tökéletesség nyilvánulhat meg, melynek a kor felfogása szerint tökéletesnek vélt körpálya felelt meg. Az impetus-elmélet, azaz az arisztotelészi rendszer tehetetlenséggel kiegészített mechanikai rendszere olyan középkori filozófusok munkája nyomán bontakozott ki a 6. században, mint Ióannész Philoponosz, ezt a munkát folytatta a 14. században többek között Jean Buridan. A holdi szféra alatti mozgásokat tökéletlennek tekintették, ezzel magyarázták, hogy a földi tárgyak nem az égi tökéletességgel konzisztens mozgást végeznek. Az ún. szublunáris tartományban az idealizált mozgáspályák csak leleményes kísérletekben voltak megfigyelhetők, ennek megfelelően a 17. század előtt sokan nem is tekintették a mesterséges kísérleteket a természetes világ megfelelő megismerési módjának. A fizikai magyarázatok a szublunáris tartományokban a hajlamok körül forogtak. A kövek a föld elemet tartalmazták, és a földes tárgyak hajlamosak voltak egyenes vonalban a Föld (és az arisztotelészi geocentrikus világképben a világegyetem) középpontja felé mozogni, hacsak meg nem akadályozta őket valami ebben.[13]
A tudományos forradalom[szerkesztés]
A 16. és 17. század folyamán Európában a tudományos forradalomként is emlegetett tudományos szemléletváltás volt a meghatározó folyamat. A régebbi filozófiai megközelítésekkel szembeni elégedetlenség már korábban erősödött, és olyan társadalmi-politikai változások mentek végbe Európában, mint a protestáns reformáció. A tudomány forradalma akkor kapott erőre, amikor a skolasztika egyre tarthatatlanabb érvei és világnézete ellen egyre több természetfilozófus kelt ki. Az új elképzelések fő irányvonala az volt, hogy a mechanika és a csillagászat törvényszerűségeire általánosan érvényes matematikai modell adható.
Kopernikusz és hatása[szerkesztés]

Az áttörést a csillagászatban Kopernikusz (1473–1543) lengyel csillagász érte el, amikor 1543-ban egy bolygómozgások rendszerezését célzó munkájában erős érveket hozott fel a Naprendszer heliocentrikus modellje mellett. A Naprendszer heliocentrikus modelljeiben a Föld más testekkel együtt a Nap körül kering. Ez az elképzelés szakított Ptolemaiosz több mint 1400 éven keresztül érvényben lévő földközéppontú világnézetével, mely a Földet helyezte a világegyetem közepébe. Bár már Szamoszi Arisztarkhosz (i. e. 310 k. – 230 k.) is javasolt olyan elméletet az i. e. 3. században, mely szerint a Föld kering a Nap körül, de Kopernikusz érvelése vezetett ezen "forradalmi" gondolat általános elfogadásához. Kopernikusz könyve, mely az elméletét közölte (De revolutionibus orbium coelestium, „Az égi pályák körforgásairól”) csak 1543-ban, közvetlenül a halála előtt jelent meg, melyet ma a modern csillagászat és a tudományos forradalom kiindulópontjának tekintünk.[forrás?] Kopernikusz új látásmódja, kiegészítve a Tycho de Brahe által végzett megfigyelésekkel, lehetővé tették Johannes Kepler (1571–1630) német csillagász számára a bolygók mozgásával kapcsolatos törvényei megfogalmazását, amiket mind a mai napig használunk.
Galileo Galilei[szerkesztés]

Galileo Galilei (1564–1642) olasz matematikus, csillagász és fizikus a tudományos forradalom egyik központi alakja volt. Osztotta a kopernikuszi nézeteket: elismerte csillagászati felfedezéseit, kísérleteiről és a távcső továbbfejlesztésével kapcsolatos eredményeit. Korának akadémiai viszonyai között a tudósoknak jellemzően a három alapvető tudományterületen (jog, orvostudomány és teológia) belül volt mozgásterük. Galilei viszony úgy vélte, hogy a műszaki tudományok eredményei már filozófiai kérdéseket feszegetnek, főleg ami a csillagászatot illeti. Ez utóbbi ugyanis rámutatott, hogy néhány bevett elképzelés, melyet a hivatalos filozófia tudományosan megalapozottnak tart, valójában egy sor matematikai törvényszerűségnek ellentmond például a Nap, a Hold és más égitestek relatív mozgását illetően. Galilei mechanikai kísérleteiben rámutatott arra, hogy a mozgás leírására egyetemes matematikai törvényszerűségek írhatók fel attól függetlenül, hogy a mozgást kiváltó ok „természetes” vagy „mesterséges” volt-e. Ez szöges ellentétben állt azzal a skolasztikus felfogással, hogy az isteni eredetű, felsőbb szférákhoz kapcsolódó jelenségek tökéletesek, így elvont matematikával leírhatók, de a földi jelenségek egy ettől eltérő világképpel magyarázandók.

Galilei a Pisai Egyetemen az orvostudományok hallgatója volt, de érdeklődése hamar átvándorolt a matematika és a fizika területére. 19 évesen felfedezte, később bebizonyította az inga izokron természetét: pulzusát használva megmérte a pisai katedrálisban lengő lámpa lengésidejét, és úgy találta, hogy a periódusidő minden lengés esetén ugyanannyi lesz, tekintet nélkül a csillapodó lengés pillanatnyi amplitúdójára. Nevezetesek még a hidrosztatikai egyensúllyal kapcsolatos eredményei és a szilárd testek gravitációs középpontjáról szóló értekezése.
Pisai Egyetemi oktatói pályafutása (1589–92) során kezdte meg a mozgó testek törvényszerűségeivel kapcsolatos kísérleteit. Egyes felfedezései olyannyira nem illeszkedtek az arisztotelészi mechanika világképébe, hogy a kortársai egy részében erős ellenérzéseket keltettek. Úgy találta például, hogy a testek nem a súlyukkal arányos sebességekkel esnek: azonos méretű, de eltérő tömegű tárgyak azonos magasságból ejtve földet éréskor azonos végsebességet érnek el. A híres történet, mely szerint Galilei súlyokat dobott le a pisai ferde toronyból, nem igazolható hitelt érdemlően. Azonban azt tudjuk, hogy kísérleteivel rámutatott a felállított mechanikai törvényeinek érvényességére. Megmutatta, hogy a lövedék röppályája (a ferde hajításra vonatkozó összefüggéseknek megfelelően) parabola, továbbá munkája megalapozta a newtoni mozgástörvények kialakulását (pl. a tehetetlenség és a viszonyítási rendszer fogalmának kimondásával). Kidolgozta a relativitás elvét, mely elsőként tesz állításokat a háromdimenziós geometrián kívüli tér és idő tulajdonságairól.[forrás?]
A csillagászati megfigyelés területén is számos maradandó eredményt ért el, ezek között kiemelkedő például a Vénusz fázisainak távcsöves megfigyelése, a Jupiter négy legnagyobb holdjának 1609-es felfedezése (melyeket ma nevezzük Galilei-holdaknak is), illetve a napfoltok megfigyelése és elemzése. Galilei alkalmazott tudománnyal is foglalkozott, több felfedezése között megemlítendő az általa kidolgozott iránytű. Felfedezése a Jupiter-holdakról 1610-ben került kiadásra, mely hatására csakhamar matematikusi és filozófusi állást kapott a Medici-udvarban. Új megbízói elvárták tőle, hogy vitába bocsátkozzon az arisztotelészi hagyomány filozófusaival. Új kiadványai széles közönséget érhettek el: a Matematikai érvelések és bizonyítások két új tudományág, a mechanika és a mozgások köréből (melyet külföldön adhatott ki a Párbeszédek a két legnagyobb világrendszerről[14] című publikáció miatti letartóztatását követően), illetve a A becsüs.[15][16]
Megosztó eredményeinek fogadtatása vegyes volt. Galilei úttörő munkája miatt kortársaitól illetve a fizika későbbi képviselőitől többféle elnevezést kapott. Nevezték a „modern megfigyelési csillagászat atyjának”,[17] a „modern fizika atyjának”,[18] a „tudomány atyjának”[18] és a „modern tudomány atyjának”.[forrás?] Stephen Hawking szerint „Galilei valószínűleg minden egyénnél nagyobb mértékben tehető felelőssé a modern tudomány születéséért.”[19] Mivel azonban a kor vallásos világképe a Naprendszer geocentrikus vagy tycho-i felfogását fogadta el érvényesnek, a heliocentrikus világkép támogatása miatt Galileit az inkvizíció perbe fogta. Az „eretnekség heves gyanújában” találtatott, kényszerítették, hogy vonja vissza állítását, és élete hátralevő részét házi őrizetben töltötte.
Galilei mozgással kapcsolatos kísérletei és matematikai leírásai újfajta hozzáállás elterjedéséhez vezettek: a kísérletezés immár a természet kutatásának fontos részévé válhatott, része lett a természetfilozófia általános módszereinek. Galilei öröksége és egyes filozófiai reformerek, mint William Gilbert és Francis Bacon által erre alapozott kísérleti szemlélete jelentős számú követőt szerzett, például Evangelista Torricelli és az Accademia del Cimento résztvevői Itáliában, Marin Mersenne és Blaise Pascal Franciaországban, Christiaan Huygens Hollandiában, és Robert Hooke, valamint Robert Boyle Angliában.
René Descartes[szerkesztés]

René Descartes francia filozófus (1596–1650) jó kapcsolatokkal és befolyással rendelkezett korának kísérleti filozófiai köreiben. Decartes ambiciózus célja a hagyományos skolasztikus filozófiai hagyománnyal való teljes szakítás volt. Megkérdőjelezte az érzékek által felfogható valóságot, és egy olyan filozófiai világképen dolgozott, melyben az összes érzékelhető jelenség törvényszerűségei egy elvont világ mozgásaival, jellemzőivel magyarázható. Az emberi gondolatot és Istent nem illesztette be világképébe, ezeket a fizikai világegyetemtől különállónak tartotta. Filozófiai rendszerében feltételezte, hogy a mozgás különböző formái, mind a látszólag tökéletes bolygómozgások, mind a korábban tökéletlennek tartott földi mozgások egyazon törvényszerűségekkel írhatók le, hiszen ezek ugyanazon jelenségek különböző aspektusai. A fizika leírásában az úgynevezett korpuszkuluszokat javasolta, melyek örvénylő mozgásával magyarázta az égitestek mozgását, illetve ezek tárgyakra kifejtett hatásával a gravitációt. Felfogása a skolasztikus felfogástól nem rugaszkodott el abban a tekintetben, hogy a fizikai térben a vákuum elvi lehetőségét kizárta.[20][21][22]
Descartes, Galieihez hasonlóan, meg volt győződve a fizikai világ matematikai magyarázatának fontosságáról. Ennek megfelelően nagy hangsúlyt fektetett a fizika matematikai módszereinek kialakítására, továbbfejlesztésére. A 17. századi matematikai és geometriai fejlődés kulcsszereplője volt. A mozgás karteziánus (azaz Descartes elveit követő) matematikai leírása szerint a fizikai jelenségek matematikai megfogalmazásának fontos eleme az igazolhatóság, mely álláspontját többek között Huygens és Gottfried Wilhelm Leibniz német filozófus is osztotta. Leibniz, követve a karteziánus hagyományt, a skolasztika elveivel szembehelyezkedve fogalmazta meg saját filozófiai alternatíváját, melyet 1714-es munkájában, a Monadológiában vázolt fel. Descartes-ot a „modern filozófia atyjának” tartják, és sok későbbi nyugati filozófiai munka az ő eredményein alapul. Az Elmélkedések az első filozófiáról című műve továbbra is fontos tudománytörténeti mérföldkőnek számít. Descartes hatása a matematikára szintén kiemelkedő. A ma is alkalmazott Descartes-koordináta-rendszer tette lehetővé algebrai egyenletek geometriai ábrázolását és tárgyalását. Őt tekintik a koordinátageometria, az algebra és a geometria közti híd atyjának, mely fontos lépés a modern analízis és függvénytan kialakulása felé vezető úton.
Isaac Newton[szerkesztés]

A 17. század végén, 18. század elején lépett színre a tudományos forradalom egyik legnagyobb alakja. Sir Isaac Newtont, a Cambridge-i Egyetem fizikusát és matematikusát, az angliai Royal Society tagját sokan a valaha élt legnagyobb hatású tudósnak tartják. Saját mechanikai és csillagászati felfedezéseit a megelőző korok eredményeivel sikeresen kombinálva hozott létre egy önálló, a világegyetem működését leíró világképet. Newton fogalmazta meg a híres mozgástörvényeket és az egyetemes tömegvonzás törvényét. Ez utóbbi nem csupán a Földön szabadon eső tárgyak, hanem égitestek viselkedését is jó közelítéssel magyarázza, mely szöges ellentétben áll a skolasztikusok által évszázadokon át hitt alsó és felső világot megosztó kettősséggel. Fizikai elveihez eredeti matematikai módszereket alkotott, a mai matematikai analízis lényegében Newton munkáján alapul (tőle függetlenül még Gottfried Leibniz hozzájárulása is jelentős ezen témakörhöz). Az analízis és a modern függvénytan a fizika későbbi vívmányaihoz nélkülözhetetlen eszközzé vált. Newton felfedezéseit a Philosophiae Naturalis Principia Mathematica („A természetfilozófia matematikai alapjai”) című művében fejtette ki. Egyesek e mű 1687-es megjelenésétől datálják a modern mechanika és csillagászat korszakának kezdetét.
Newton szembehelyezkedett a karteziánus mechanikai világképpel, mely minden mozgást a korpuszkuluszok által kifejtett közvetlen hatás figyelembe vételével magyaráz meg. Mozgástörvényei és a gravitációs törvény alkalmazásával Newton sikerrel mutatott rá arra, hogy nem csak a tökéletes formák mentén mozgó testek (például az égitestek) pályája határozható meg, de valójában minden mozgó test pályájának jövőbeli alakulására lehet következtetni a test helyzete, tömege, sebessége és a rá ható erők ismeretében. Azonban a megfigyelt égi mozgások nem feleltek meg pontosan az elgondolásának. A teológia iránt is élénken érdeklődő Newton ebben az egyensúlyt fenntartani igyekvő isteni beavatkozás bizonyítékát látta.

Newton fizikai elveit vitatták a kontinentális Európa filozófusai, akik a mozgás és a gravitációs filozófia metafizikai magyarázatának a hiányát elfogadhatatlannak találták. 1700-tól kezdődően egyre szélesedett a szakadék a Newtonhoz húzó brit és az azzal szembehelyezkedő más európai filozófiai elképzelések között. Továbbá éles vita bontakozott ki azzal kapcsolatban is, hogy a matematikai analízis új témaköre, mellyel Newton és Leibniz egymástól függetlenül foglalkozott, pontosan kinek is az eredménye. Ezt mutatja, hogy az Európa szerte elterjedt, Leibniz-féle jelöléseket a Nagy-Britanniában nem alkalmazták.
Bár Newton maga is szükségét érezte a gravitáció metafizikai háttere megértésének, nyilvánosan következetesen elutasította az erre utaló bírálatokat és azt hangoztatta, hogy a gravitáció leírható úgy is, hogy annak filozófiai hátterét homály fedi. A 18. század előrehaladtával az európai természetfilozófusok fokozatosan egyre inkább belátták, hogy a testek mozgásának newtoni matematikai leírását azok ontológiai metafizikai magyarázatai nélkül is el lehet fogadni.[23][24][25]
Newton építette az első működőképes tükrös távcsövet,[26] és Optika című művében közreadva kifejtette a színek elméletét. Ezt saját, prizmával végzett kísérleteire alapozta, melyben azt tapasztalta, hogy a prizmára eső fehér fény sokféle színre, komponenseire bomlik. Newton elképzelése az volt, hogy a fény apró részecskékből áll. Ez ellentétben állt Christiaan Huygens 1690-ben bemutatott elméletével, mely szerint a fény hullámtermészetű sugárzás. Newton elismertségének, és munkájába vetett feltétlen hitnek köszönhetően a hullámtermészetű fény képét egészen a 19. századig lényegében mellőzték, úgy vélték, hogy azt Newton mechanikai képe meghaladta. Newton ezen kívül a lehűlés egy tapasztalati törvényét is kimondta, tanulmányozta a hangsebességet, vizsgálta a hatványsorokat, kidolgozta az általánosított binomiális tételt, és kifejlesztette a ma Newton-módszernek nevezett iteratív numerikus eljárást egy függvény zérushelyeinek közelítésére. A végtelen sorokról szóló eredményeit Simon Stevin tizedes törtekkel kapcsolatos munkája ihlette.[27] Legfontosabb eredménye azonban valószínűleg az, hogy gravitációs törvényével megmutatta, hogy az égi és földi testek mozgását azonos törvényszerűségek alakítják, melyek matematikailag egyaránt jósolhatók. Az égitestek mozgását leíró Kepler-törvények és a saját gravitációs elmélete közti összhang lesöpörte az asztalról a heliocentrikus világképpel kapcsolatos utolsó kételyeket is. A tudományos forradalom számtalan eredményének közös elméletbe foglalásával lefektette a modern természettudomány alapjait.
Egyéb vívmányok[szerkesztés]
A tudományos forradalom korában a fizika más ágai is fokozott figyelmet kaptak. William Gilbert, I. Erzsébet királynő udvari fizikusa 1600-ban egy mágnességről szóló munkájában, a Földet, mint hatalmas mágnest írta le. Robert Boyle (1627–1691) ír fizikus, kémikus a zárt rendszerbeli gázok viselkedését tanulmányozta, és megfogalmazta a ma Boyle–Mariotte-gáztörvénynek nevezett összefüggést. Boyle ezen kívül az élettan és a modern kémia megalapozásához is hozzájárult. 1690-ben Jakob Bernoulli megmutatta, hogy a ciklois a megoldás a tautochron problémára, és a következő évben, 1691-ben Johann Bernoulli megmutatta, hogy egy két pontról szabadon lógó lánc a láncgörbe alakját fogja felvenni, a lehető legalacsonyabb gravitációs középponttal rendelkező görbét, amit egy lánc két rögzített pont között felvehet. Később, 1696-ban megmutatta, hogy a ciklois a megoldás a brachistochron problémára.
A tudományos forradalom idején jellemző volt a különböző országokban a tudóstársaságok és akadémiák megjelenése. Ezek közül a legkorábbiak itáliai és német területeken jöttek létre, de rövid életűnek bizonyultak. Sokkal befolyásosabbak voltak a Royal Society (1660) és a Francia Tudományos Akadémia (1666). Előbbi egy magánintézmény volt Londonban, és olyan tudósokat tudott soraiban, mint John Wallis, William Brouncker, Thomas Sydenham, John Mayow és Christopher Wren (aki nem csak az építészethez járult hozzá, hanem a csillagászathoz és az anatómiához is); míg utóbbi egy párizsi kormányzati intézmény volt, ami például külföldi tagjai közt tartotta számon a holland Huygenst is. A 18. században királyi akadémiákat alapítottak Berlinben (1700) és Szentpétervárott (1724). A társaságok és akadémiák biztosították a tudományos forradalom alatt és utána az elsődleges lehetőséget a tudományos eredmények megjelentetésére és vitájára.
Termodinamika[szerkesztés]
Az erőgép előfutárát Otto von Guericke német tudós tervezte, aki 1650-ben megtervezte és megépítette a világ első vákuumszivattyúját, és a világ valaha volt első vákuumát hozta létre a magdeburgi féltekékként ismert kísérletben. A vákuum előállítására az vitte, hogy megcáfolja Arisztotelész sokáig fennálló vélekedését, miszerint a természet retteg a vákuumtól. Nem sokkal ezután Boyle tudomást szerzett Guericke terveiről, és 1656-ban Robert Hooke angol tudóssal egyeztetve egy levegőszivattyút épített. Ezen szivattyú használatával Boyle és Hooke felfigyelt a gáz nyomás-térfogat korrelációjára: PV = k, ahol P a nyomás, V a térfogat és a k egy állandó: ezt az összefüggést ma Boyle–Mariotte-törvénynek nevezzük. A korszak tudósai a levegőt egy mozdulatlan részecskékből álló rendszernek feltételezték, nem feltételezték benne mozgó molekulák jelenlétét. A hőmozgás elképzelése csak két évszázaddal később merült fel. Ezért Boyle publikációja 1660-ban a levegő mechanikai modelljét adta meg, azaz a levegőt, mint összenyomható, rugalmas közeget jellemezte.[28]
Később, a hőmérő feltalálása után az anyagok hőmérsékletét már számszerűsíteni lehetett. Ez az eszköz tette lehetővé Gay-Lussac számára, hogy felállítsa gáztörvényeit, amely nem sokkal később az ideális gáztörvény kimondásához vezetett. Denis Papin 1679-ben, már a gáztörvény kimondása előtt is, épített egy fűthető gáztartályt alkalmazó készüléket, mely nagynyomású eljárásokhoz volt használatos, és amely a mai autokláv illetve a kuktafazék elődje. A későbbi tervek már tartalmaztak egy gőznyomáscsökkentő szelepet, hogy megakadályozzák a gép felrobbanását. A szelep ütemes fel-le mozgását látva Papinben megfogant egy dugattyús-hengeres erőgép ötlete, ezen elképzelését azonban nem vitte véghez. 1697-ben Papin tervei alapján építette meg az első gőzgépet Thomas Savery mérnök. Habár ezek a korai erőgépek energiahatékonységa még igen csekély volt, mégis felkeltették a kor tudósainak a figyelmét.
A Savery-erőgép feltalálása előtt Angliában lóvontatással mozgatták az elárasztott sóbányákból a víz kiemeléséhez használt csigákat. Az elkövetkező években a gőzgépek több változata is megépült, például a Newcomen-erőgép, illetve a Watt-erőgép. A korai eszközök fejlesztésének célja a lovak helyettesítése volt, ezért minden erőgéphez egy bizonyos „lóerőt” társítottak attól függően, hogy hány lovat volt képes helyettesíteni. A legfőbb probléma ezekkel az első erőgépekkel az volt, hogy lassúak és kis hatékonyságúak voltak, a tüzelőanyaggal betáplált elméleti energiának csak kevesebb mint 2%-át alakították hasznos munkává. Más szóval, nagy mennyiségű szenet (vagy fát) kellett elégetni, hogy a kimeneti munka kis hányadát kinyerjék. Ezen működés optimalizálására külön mérnöki területek jelentek meg, ezt tekinthetjük például a korai hajtástechnika kezdetének.
A 18. századi fejlemények[szerkesztés]
A 18. század folyamán a Newton által megalapozott mechanikai képet számos tudós fejlesztette tovább, melyre fontos hatást gyakorolt a matematikai analízis fejlődése. A mechanikai problémák függvénytant és analízist alkalmazó megoldásait tárgyaló fizikai területet ekkor racionális mechanikának nevezték, melyre ma a klasszikus mechanika kifejezést használjuk.
Mechanika[szerkesztés]

1714-ben Brook Taylor egy differenciálegyenlet megoldásával meghatározta egy adott hosszúságú kifeszített rezgő húr alapfrekvenciájának függését a húrt feszítő erő és az egységnyi hosszra eső tömeg függvényében. Daniel Bernoulli svájci matematikus fontos eredményeket ért el a gázok viselkedésének matematikai leírása terén, mellyel az egy évszázaddal később kifejlesztett gázelmélet és áramlástan alapjait fektette le. Ezen eredményei kapcsán tartják őt a matematikai fizika első képviselőjének is.[29] Bernoulli 1733-ban egy differenciálegyenlet megoldásával levezette a függő lánc alapfrekvenciáját és harmonikusait, továbbá 1734-ben megoldotta az egyik végén befogott hajlékony rúd rezgéseinek a differenciálegyenletét. Bernoulli folyadékdinamikai eljárásai és a folyadék áramlásának vizsgálata 1738-as Hydrodynamica című munkájában került be bemutatásra.
E korban a racionális mechanikát művelő fizikusok a newtoni elvekre támaszkodva a megfigyelt mozgások matematikai modelljeinek kifejlesztésével foglalkoztak. A tiszta matematikai modellek ezen kívül fontos közelítő módszerekkel egészültek ki, melyek olykor megkönnyítik, máskor egyenesen lehetővé teszik egy adott probléma matematikai megfogalmazását, leírását. E témában kiemelkedőek Horváth Keresztély János magyar jezsuita egyetemi tanár összefoglaló írásai. A 18. század végére az analitikai eljárások már kellőképpen pontosak voltak a Naprendszer stabilitásának kizárólag a newtoni törvényekkel való magyarázatára. Ugyan még az olyan egyszerű fizikai rendszerek determinisztikus leírására sem volt lehetőség, mint a háromtest-probléma, ez elvben nagy lépés volt afelé, hogy isteni beavatkozástól független fizikai kép alakulhasson ki a világegyetem főbb összefüggéseiről.[30] 1705-ben Edmond Halley előrejelezte a Halley-üstökös periodicitását, 1781-ben William Herschel felfedezte az Uránuszt, és 1798-ban Henry Cavendish megmérte a gravitációs állandót és meghatározta a Föld tömegét. 1783-ban tette közzé John Michell azon feltevését, hogy egyes objektumok olyan nagy tömegűek lehetnek, hogy még a fény sem szökhet ki belőlük. Ma az ilyen testeket fekete lyukaknak nevezzük.
1739-ben Leonhard Euler megoldotta a gerjesztett harmonikus oszcillátor differenciálegyenletét, és észlelte a rezonancia jelenségét. 1742-ben Colin Maclaurin felfedezte egységesen forgó öngravitációs szferoidjait. 1742-ben Benjamin Robins megjelentette New Principles in Gunnery (Új elvek az ágyúzástanban) című művét, mellyel megalapozta az aerodinamika, azaz a gázok áramlásának tudományát. E században a kontinentális Európa kutatói, például Bernoulli, Euler, Lagrange, Laplace és Legendre is nagy eredményeket mutattak fel. 1743-ban Jean le Rond d’Alembert megjelentette Traite de Dynamique című művét, amelyben a bizonyos kényszerfeltételeknek megfelelő általános erőkre vonatkozó elveit írta le. Összetett fizikai rendszerek dinamikai problémáinak megoldására bevezette a virtuális munka elképzelését, ami a D’Alembert-elv fontos eleme, és a modern mechanika modern elveinek kiindulópontja. 1747-ben Pierre Louis Maupertuis megalkotott egy elvet, mely a ma alkalmazott legkisebb hatás elvének alapja volt. 1759-ben Euler megoldotta a négyszögletű dob rezgéseinek parciális differenciálegyenletét. 1764-ben Euler megvizsgálta a kör alakú dob rezgéseinek a parciális differenciálegyenletét, és megtalálta az egyik, Bessel-függvénnyel megadható megoldást. 1776-ban John Smeaton megjelentette művét a teljesítménnyel, a munkával, a lendülettel és a mozgási energiával kapcsolatos kísérletekről, és az energiamegmaradás alátámasztásáról. 1788-ban Joseph Louis Lagrange a Mécanique Analytique-ban először vezette be a később róla elnevezett a Lagrange-függvényt, amely egy mechanikai rendszer leírására alkalmazható: ha a virtuális munkára alapozva egy rendszer Lagrange-függvénye megadható, akkor azt beírva az Euler–Lagrange-egyenletbe, abból meghatározhatók a rendszer Newtoni mozgásegyenletei. 1789-ben Antoine Lavoisier kimondta a tömegmegmaradás törvényét.
Termodinamika[szerkesztés]
A 18. század során a termodinamika a súlytalan „imponderábilis folyadékok” elméletein keresztül fejlődött, mint a hő („kalorika”), az elektromosság és a flogiszton (amely gyorsan megbukott azt követően, hogy Lavoisier a század vége felé azonosította az oxigéngázt). Feltételezve, hogy ezek az elképzelések valódi folyadékok, áramlásuk nyomon követhető egy mechanikai eszközkészlettel vagy vegyi reakciókkal. A kísérletezés ezen hagyománya egy újfajta kísérleti eszköztár kifejlődéséhez vezetett, mint a Leideni palack, és újfajta mérőműszerekhez, mint a kaloriméter, valamint a régiek fejlettebb változataihoz, mint a hőmérő. A kísérletek új elképzeléseket is szültek, mint Joseph Black (1728–99), a Glasgow-i Egyetem kísérletezője által megfigyelt látens hő, és Benjamin Franklin philadelphiai értelmiségi jellemzése az elektromos folyadékokról, mint a többlet és a hiány helyei közti áramlásról (az elképzelést később újraértelmezte a pozitív és negatív töltések fogalmaival). Úgyszintén Franklin mutatta meg 1752-ben, hogy a villámlás elektromosság.
A 18. században a hő elfogadott elmélete azt a kalorikának nevezett egyfajta folyadéknak tekintette; bár ez az elmélet a későbbiek folyamán hibásnak bizonyult, számos hozzá ragaszkodó tudós tett a modern elmélet kifejlesztésénél felhasznált fontos felfedezéseket, köztük Joseph Black és Henry Cavendish (1731–1810). A kalorikus elmélettel ellentétben, amit főleg a vegyészek fejlesztettek ki, egy kevésbé elfogadott, Newton idejéig visszanyúló elmélet volt, hogy a hőt az alkotórészek részecskéinek a mozgása okozza. Ez a mechanikai elmélet alátámasztást nyert 1798-ban Rumford grófjának (Benjamin Thompson) ágyúcsőfúrási kísérletei során, aki közvetlen összefüggést talált a hő és a mechanikai energia között.
Habár már a kora 18. században felismerték, hogy az elektrosztatikus és mágneses erők Newton mozgáselveihez hasonlatos abszolút elméleteinek a megtalálása egy fontos vívmány lenne, egyik sem következett be. A lehetetlensége ennek csak lassan tűnt el, ahogyan a kísérleti gyakorlat sokkal elterjedtebbé és finomabbá vált a 19. század korai éveiben olyan helyeken, mint az újonnan alapított londoni Royal Institution. Eközben a racionális mechanika analitikai módszereit elkezdték alkalmazni a kísérleti jelenségekre, legnagyobb hatású Joseph Fourier francia matematikus analitikai eljárása volt a hőáramlás kapcsán, ahogy az 1822-ben kiadták.[31][32][33] Joseph Priestley 1767-ben javaslatot tett egy elektromos inverz négyzetes törvényre, és Charles Augustin de Coulomb 1798-ban bevezette az elektrosztatika inverz négyzetes törvényét.
A század vége felé a Francia Tudományos Akadémia tagjai egyértelmű fölényt alakítottak ki a tudományterületen.[25][34][35][36] Ezzel egy időben a Galileo és követői által megalapított kísérleti hagyomány kitartott. A Royal Society és a Francia Tudományos Akadémia voltak a fő központjai a kísérleti munka végzésének és beszámolóinak. A 18. század folyamán a kísérletek a mechanika, a fénytan, a mágnesesség, a statikus elektromosság, a kémia és az élettan területéről nem voltak élesen elválasztva egymástól, de jelentős magyarázatbeli, és ezáltal kísérleti tervezési különbségek bukkantak elő. A kémiai kísérletezők például ellenálltak annak, hogy az absztrakt newtoni erők sémáit próbálják meg ráerőltetni a kémiai kötésekre, és ehelyett a kémiai összetevők és reakciók izolálására és osztályozására összpontosítottak.[37]
A 19. század[szerkesztés]


1800-ban Alessandro Volta (1745–1827) felfedezte az elektromos elemet (voltai halom néven ismert) és ezzel kitágította az elektromos áramok vizsgálatának módszereit. Egy évvel később Thomas Young bemutatta a fény hullámtermészetét – amelyet kísérletileg erősen megtámogatott Augustin-Jean Fresnel munkája – és az interferencia elvét. 1813-ban Peter Ewart A mozgó erő mértékéről című értekezésében alátámasztotta az energiamegmaradás gondolatát. 1820-ban Hans Christian Ørsted úgy találta, hogy az áramjárta vezető növeli az őt körülvevő mágneses erőt, és egy héten belül Ørsted felfedezése elérte Franciaországot, André-Marie Ampère felfedezte, hogy két párhuzamos elektromos áram erővel fog hatni egymásra. 1821-ben William Hamilton elkezdte a Hamilton-féle karakterisztikus függvény elemzését. 1821-ben Michael Faraday (1791–1867) épített egy elektromosan hajtott motort, míg Georg Ohm 1826-ban kijelentette törvényét az elektromos ellenállásról, mely a feszültség, az áram és az ellenállás közti összefüggést fejezi ki egy elektromos áramkörben. Egy évvel később Robert Brown botanikus felfedezte a Brown-mozgást: a pollenszemcsék vízben a folyadékban levő gyorsan mozgó atomok és molekulák bombázásának hatására mozgásban jönnek. 1829-ben Gaspard Coriolis bevezette a munka (erő szorozva távolság) és a mozgási energia fogalmát a mai jelentésükkel.
1831-ben Faraday (és tőle függetlenül Joseph Henry) felfedezte a fordított hatást, elektromos potenciál vagy áram keletkezését mágnesesség által, ami elektromágneses indukcióként ismert; ez a két felfedezés az alapja a villanymotornak, ill. a villanygenerátornak. 1834-ben Carl Jacobi felfedezte az egyenletesen forgó öngravitációs ellipszoidjait (a Jacobi ellipszoidot). 1834-ben John Russell Edinburgh közelében a Union Csatornában megfigyelte a nem széteső, magányos vízhullámot (szoliton), és egy víztartályt használt a magányos vízhullám sebességfüggőségének a vizsgálatára a hullámamplitúdóval és a vízmélységgel összefüggésben. 1835-ben William Hamilton kijelentette a Hamilton-féle kanonikus mozgásegyenletet. Ugyanezen évben Gaspard Coriolis elméletileg is megvizsgálta a vízikerekek mechanikai hatásfokát, és levezette a Coriolis-hatást. 1841-ben Julius Robert von Mayer, egy amatőr tudós írt egy értekezést az energia megmaradásáról, de akadémiai tanulmányainak hiánya annak elutasításához vezetett. 1842-ben Christian Doppler javaslatot tett a Doppler-hatásra. 1847-ben Hermann von Helmholtz hivatalosan is kimondta az energiamegmaradás törvényét. 1851-ben Léon Foucault megmutatta a Föld forgását és hatalmas fizikai ingával (Foucault-inga).
A század első felében fontos előrelépések történtek a kontinuummechanika területén, mégpedig a rugalmasság törvényei szilárd testek esetén és a Navier–Stokes-egyenletek felfedezése folyadékok esetén.
A termodinamika törvényei[szerkesztés]

(1824–1907)
A 19. században a hő és a mechanikai energia közti kapcsolat mennyiségi kifejezése Julius Robert von Mayer és James Prescott Joule nevéhez fűződik, akik az 1840-es években megmérték a hő mechanikai megfelelőjét. 1849-ben Joule közölte kísérletsorozatának eredményeit (köztük a lapátkerék kísérletét), amik megmutatták, hogy a hő az energia egyik formája; ez a tény az 1850-es években lett elfogadott. A hő és az energia közti összefüggés fontos volt a gőzgépek fejlődése szempontjából, és 1824-ben jelentette meg Sadi Carnot kísérleti és elméleti munkáját. Carnot az idealizált gép hatékonyságáról szóló értekezésébe belefoglalta a termodinamika néhány gondolatát. Sadi Carnot munkája lett az alapja a termodinamika első törvényének – ami az energiamegmaradás törvényének az újrafogalmazása –, ezt 1850 körül, a később Lord Kelvinként ismert William Thomson (1824–1907) és Rudolf Clausius mondtak ki. Lord Kelvin, aki 1848-ban az abszolút nulla elképzelését a gázokról kiterjesztette az összes alkotóelemre, Lazare Carnot, Sadi Carnot és Émile Clapeyron mérnöki elméletére épített – valamint James Prescott Joule kísérletezésére a munka mechanikai, kémiai, hő- és elektromos formáinak felcserélhetősége tárgyában –, hogy kialakítsa az első törvényt.
Kelvin és Clausius kimondta a termodinamika második törvényét is, amely eredetileg azt a tényt vette figyelembe, hogy a hő spontán módon nem áramlik a hidegebb testből a melegebbe. Gyorsan követték más kifejezései is (például a második törvényt kifejtette Thomson és Peter Guthrie Tait nagy hatású munkájában, az Értekezés a természetfilozófiáról című műben), és főként Kelvin értette meg a második törvény általános következményeit. A második törvény alapja az az elképzelés volt, hogy a gázok mozgásban levő molekulákból állnak, ennek egyes részleteiről Bernoulli már 1738-ban értekezett, de a gondolat kegyvesztett lett, mígnem 1857-ben Clausius élesztette újjá. 1850-ben Hippolyte Fizeau és Léon Foucault megmérte a fény sebességét vízben, és úgy találták, hogy lassabb, mint a levegőben, ami a fény hullámmodelljét támasztotta alá. 1852-ben Joule és Thomson bemutatta, hogy a sebesen táguló gáz lehűl, később ezt nevezték Joule–Thomson- vagy Joule–Kelvin-hatásnak. Hermann von Helmholtz 1854-ben felvetette a világegyetem hőhalálának a gondolatát, ugyanabban az évben, amikor Clausius megállapította a dQ/T (Clausius-tétel) fontosságát (habár még nem nevezte el ezt a mennyiséget).
Statisztikus mechanika (egy alapvetően új tudományos megközelítés)[szerkesztés]

1859-ben James Clerk Maxwell (1831–1879) felfedezte a molekuláris sebességek eloszlási törvényét. Maxwell megmutatta, hogy az elektromos és mágneses mezők forrásukból kifelé a fény sebességével egyenlő sebességgel terjednek, és hogy a fény az elektromágneses sugárzás számos fajtájának az egyike, mely a többitől csak frekvenciában és hullámhosszban különbözik. 1859-ben Maxwell kidolgozta a gázmolekulák sebességeloszlásának a matematikáját. A fény hullámelmélete széles körben elfogadott volt Maxwell elektromágneses mezőről szóló munkája idején, és ezek után a fény vizsgálata, valamint az elektromosságé és a mágnesességé szoros kapcsolatban volt egymással. 1864-ben Maxwell megjelentette tanulmányát az elektromágneses mező egy dinamikus elméletéről, és 1873-as, Értekezés az elektromosságról és a mágnesességről című publikációjában azt állította, hogy a fény egy elektromágneses jelenség. Ez a mű olyan német teoretikusok elméleti munkájára épített, mint Carl Friedrich Gauss és Wilhelm Weber. A hő belefoglalása a részecskemozgásba, és az elektromágneses erők hozzáadása a newtoni dinamikához egy hatalmas elméleti alátámasztást adott a fizikai megfigyeléseknek.
Az előrejelzés, hogy a fény egy hullám alakú energiaátvitelt jelent az éterben, és ennek az előrejelzésnek a látszólagos megerősítése azáltal, hogy a Helmholtz-tanítvány Heinrich Hertz 1888-ban érzékelte az elektromágneses sugárzást, egy jelentős diadala volt a fizikai elméletnek, és felvetette annak a lehetőségét, hogy a mezőre alapozva nemsokára még alapvetőbb elméletek is kifejleszthetők.[38][39][40][41] Maxwell elméletének kísérleti megerősítését Hertz szolgáltatta, aki 1886-ban elektromos hullámokat generált és érzékelt, valamint igazolta tulajdonságaikat, ezzel egy időben előrevetítette alkalmazásukat a rádióban, a tévében és más készülékekben. 1887-ben Heinrich Hertz felfedezte a fényelektromos jelenséget. Az elektromágneses hullámok kutatása hamarosan elkezdődött, számos tudós és feltaláló végzett kísérleteket a tulajdonságaikkal kapcsolatban. Az 1890-es évek második felében Guglielmo Marconi kifejlesztett egy rádióhullámon alapuló vezeték nélküli telegráf rendszert[42] (ld. a rádió feltalálása).
Az anyag atomelméletét vetette fel újra a 19. század elején John Dalton vegyész, és a Clausius és James Clerk Maxwell által kifejlesztett kinetikus-molekuláris gázelmélet egyik hipotézise lett, hogy megmagyarázza a termodinamika törvényeit.

(1844-1906)
A kinetikus elmélet viszont Ludwig Boltzmann (1844–1906) és Josiah Willard Gibbs (1839–1903) egy forradalmian új megközelítéshez vezetett a tudományban, a statisztikus mechanikához, mely egy rendszer mikroállapotainak statisztikáját tanulmányozza és a statisztikát használja egy fizikai rendszer állapotának meghatározásához. Ezen részecskék szerveződési állapotainak statisztikai valószínűsége és ezen állapotok energiáinak kölcsönös kapcsolatba hozásával Clausius az energia disszipációját a növekvő valószínűségű, egyre szervezetlenebb állapotok felé történő molekuláris konfigurációk statisztikai tendenciájaként értelmezte újra (megalkotva az entrópia fogalmát, hogy leírja egy állapot szervezetlenségét). A termodinamika második törvényének statisztikai kontra abszolút értelmezése egy több évtizeden át tartó vitát indított el (olyan érveket teremtve, mint Maxwell-démon), amelyet addig nem tekintettek véglegesen lezártnak, amíg a korai 20. században az atomok viselkedését szilárdan meg nem állapították.[43][44] 1902-ben James Jeans megtalálta a statikus, közel egynemű közegben növekvő gravitációs perturbációkhoz szükséges hosszúsági skálát.
A 20. század: a modern fizika születése[szerkesztés]

A 19. század végére a fizika eljutott arra a pontra, ahol a klasszikus mechanika meg tudott birkózni a makroszkopikus szituációkat érintő nagyon komplex problémákkal, a termodinamika és a mozgáselmélet jól megalapozott volt, a geometriai és fizikai fénytan megérthető volt az elektromágneses hullámok fogalmaival, és az energia és lendület (és tömeg) megmaradásának törvényei széles körben elfogadottak voltak. Annyira alaposak voltak ezek és más fejlődések, hogy általánosan elfogadott volt, hogy a fizika összes fontos törvényét felfedezték, és kifolyólag a kutatás a kisebb problémák tisztázásával, és különösen a módszer és mérés továbbfejlesztésével lesz elfoglalva. Azonban 1900 körül komoly kételyek merültek fel a klasszikus elméletek teljességével – Maxwell elméleteinek győzelmét például aláásták a következetlenségek, amik már kezdtek megjelenni – és alkalmatlanságukkal kapcsolatban bizonyos fizikai jelenségek magyarázatával kapcsolatban, mint a feketetest-sugárzás energiaeloszlása és a fényelektromos jelenség, míg egyes elméleti megfogalmazások paradoxonokat eredményeztek határértékeik esetén. Neves tudósok, mint Hendrik Lorentz, Emil Cohn, Ernst Wiechert és Wilhelm Wien azt hitték, hogy a Maxwell-egyenletek valamiféle módosításai képezhetik majd az összes fizikai törvény alapját. A klasszikus fizika ezen hiányosságait azonban soha sem sikerült feloldani, és új ötletekre volt szükség. A 20. század elején nagy forradalom rázta meg a fizika világát, amely egy új korszakhoz vezetett, amit általában modern fizikaként emlegetünk.[45]
Sugárzási kísérletek[szerkesztés]

A 19. században a kísérletezők a sugárzás váratlan formáit kezdték el észlelni: Wilhelm Röntgen szenzációt keltett a röntgensugarak 1895-ös felfedezésével; 1896-ban Henri Becquerel felfedezte, hogy az anyag bizonyos fajtái önmaguktól sugárzást bocsátanak ki. 1897-ben Joseph John Thomson (1856–1940) felfedezte az elektront, és a Marie és Pierre Curie által felfedezett új radioaktív elemek kérdéseket vetettek fel az eddig megbonthatatlannak tartott atommal és az anyag természetével kapcsolatban. Marie és Pierre megalkotta a radioaktivitás kifejezést az anyag ezen tulajdonságának a leírására, és izolálták a rádium és polónium radioaktív elemeket. Ernest Rutherford és Frederick Soddy elektronok és a hélium elem segítségével azonosított Becquerel sugárzási formái közül kettőt. Rutherford a radioaktivitás két formáját azonosította és nevezte el, és 1911-ben a kísérleti bizonyítást akként értelmezte, hogy az atom egy sűrű, pozitív töltésű magból áll, körülvéve negatív töltésű elektronokkal. A klasszikus elmélet azonban azt jelezte előre, hogy ez a szerkezet instabil lenne. A klasszikus elmélet két másik kísérleti eredményt sem volt képes sikeresen megmagyarázni, amelyek a késő 19. században bukkantak fel. Egyike ezeknek az Albert A. Michelson és Edward W. Morley általi szemléltetés – amely a Michelson–Morley-kísérletként ismert –, mely megmutatta, az elektromágneses jelenségek leírásához valószínűleg nem létezik egy preferált, az éterhez képest nyugalomban levő a hipotetikus koordináta-rendszer. Az 1930-as évek folyamán a sugárzás és a radioaktív bomlás tanulmányozása maradt továbbra is a fizikai és kémiai kutatás elsődleges fókuszában, amikor is a maghasadás megnyitotta az utat a gyakorlati kihasználása felé annak, amit azóta atomenergiának hívunk.
Albert Einstein relativitáselmélete[szerkesztés]
1905-ben egy Albert Einstein (1879–1955) nevű fiatal, 26 éves német fizikus (akkoriban berni szabadalmi hivatalnok) megmutatta, hogyan hat a megfigyelő és az, amit megfigyel, közti mozgás az idő és a tér mérésére. Nem túlzás azt mondani, hogy Einstein radikális relativitáselmélete forradalmasította a tudományt. Habár Einsteinnek számos egyéb fontos hozzájárulása volt a tudományhoz, maga a relativitáselmélet a valaha volt legnagyobb intellektuális vívmányt képviseli. Bár a relativitás ötletét nem Einstein vezette be, az ő fő hozzájárulása annak a felismerése volt, hogy a fény sebessége vákuumban állandó, azaz minden megfigyelő számára egyforma, és a mozgás számára egy abszolút fizikai határ. Ez nincs hatással az emberek hétköznapi életére, mivel a legtöbb tárgy a fénysebességnél sokkal kisebb sebességgel utazik. A fény sebességéhez közel utazó tárgyak esetén azonban a relativitáselmélet megmutatja, hogy az ezekhez a tárgyakhoz társított órák sokkal lassabban fognak ketyegni, és hogy a földi megfigyelő mérései alapján a tárgyak rövidülnek. Szintén Einstein vezette le a híres egyenletet, E = mc², amely a tömeg és energia ekvivalenciáját fejezi ki.
Speciális relativitáselmélet[szerkesztés]

Einstein úgy érvelt, hogy a fény sebessége állandó az összes inerciarendszerben, és hogy az elektromágneses törvények érvényesek maradnak, függetlenül a vonatkoztatási rendszertől – ezek az állítások az étert a fizikai elmélet szempontjából „nélkülözhetőnek” minősítették, és ez az elmélet (amit később „speciális relativitáselméletnek” neveztek el) pedig úgy tartotta, az idő és hossz megfigyelései ahhoz viszonyítva változtak, hogy a megfigyelő hogyan mozgott a mért tárgyhoz képest. Abból is következett ez, hogy a tömeg és az energia az E=mc² egyenlet alapján felcserélhető mennyiségek. Egy ugyanezen évben megjelentetett másik írásban Einstein azt állította, hogy az elektromágneses sugárzás átvitele diszkrét mennyiségekben, „kvantumokban” történik, egy állandó alapján, amit Max Planck elméleti fizikus rögzített 1900-ban, hogy eljusson a feketetest-sugárzás eloszlásának pontos elméletéhez – ez a feltételezés megmagyarázta a fényelektromos jelenség furcsa tulajdonságait.
A speciális relativitáselmélet a fizikai megfigyelések, valamint a tér és idő elképzelései közti összefüggés egy megfogalmazása. Az elmélet az elektromágnesesség és a newtoni mechanika közti ellentmondásokból nőtt ki, és mindkét területre nagy hatással volt. Az eredeti, történeti probléma az volt, van-e értelme az elektromágneses hullámokat közvetítő „éterről” és a hozzá viszonyított mozgásról beszélni, és vajon érzékelhető-e egy ilyen mozgás, amint arra a Michelson–Morley-kísérlet sikertelenül kísérletet tett. Einstein speciális relativitáselméletében lerombolta ezeket a kérdéseket és az éter elképzelését. Azonban alapvető megfogalmazása nem tartalmazott részletes elektromágneses elméletet. Mindez a „Mi az idő?” kérdésből ered. Newton Princípiumaiban (1686) egyértelmű választ adott: „Az abszolút, valóságos és matematikai idő önmagában véve és lényegének megfelelően, minden külső vonatkozás nélkül egyenletesen múlik, és más szóval időtartamnak is nevezhető.” Ez a meghatározás alapvető az egész klasszikus fizikában.
Einstein megkérdőjelezte ezt, és úgy találta, hogy nem teljes. Ehelyett minden „megfigyelő” szükségszerűen a saját időskáláját használja, és két egymáshoz képest relatív mozgásban levő megfigyelő időskálája különbözni fog. Ebből következik a helyzet mérésének kapcsolódó hatása. A tér és az idő egymásba fonódott elképzelések lettek, alapjában véve a megfigyelőtől függnek. Mindegyik megfigyelő a saját tér-idő keretrendszerét vagy koordináta-rendszerét felügyeli. Minekutána nem létezik abszolút vonatkoztatási rendszer, adott események minden megfigyelője különböző, de egyformán érvényes (és összeegyeztethető) méréseket végez. Ami abszolút marad, az Einstein relativitás posztulátumában van kijelentve: „A fizika alapvető törvényei azonosak két megfigyelő számára, akik egymáshoz viszonyítva állandó relatív sebességgel rendelkeznek.”
A speciális relativitáselméletnek mélyreható hatása van a fizikában: az elektromágneses elmélet újragondolásaként indulva a természet egy új, manapság Poincaré-szimmetriának hívott szimmetriatörvényét találta meg, ami átvette a régi Galilei-szimmetria (ld. fentebb) helyét.
A speciális relativitáselmélet másik tartós hatását a dinamikára gyakorolta. Bár kezdetben a tömeg és energia egyesítését tulajdonították neki, nyilvánvalóvá vált, hogy a relativisztikus dinamika határozottan különbséget tett a nyugalmi tömeg, mely egy invariáns (megfigyelőtől független) tulajdonsága a részecskének vagy részecskék rendszerének, valamint egy rendszer energiája és lendülete között. A részecskefizikában a tömeg fogalma egy szemantikai változáson ment keresztül, és a késő 20. századtól szinte kizárólag a nyugalmi (vagy invariáns) tömeget jelöli. A további értekezéshez ld. tömeg a speciális relativitáselméletben.
Általános relativitáselmélet[szerkesztés]

1916-ra Einstein képes volt ezt tovább általánosítani, kezelni a mozgás minden állapotát, beleértve a nem egyenletes gyorsulást is, ami így a relativitás általános elméletévé vált. Ebben az elméletben Einstein egy új elképzelést is megad, a tér-idő görbületét, amely a tér minden pontjában leírja a gravitációs hatást. Tulajdonképpen a tér-idő görbülete teljesen átvette a newtoni univerzális gravitációs törvény helyét. Einstein szerint a gravitáció normál értelemben egyfajta illúzió, amit a tér geometriája okoz. Egy tömeg jelenléte a tömeg közelében a tér-idő görbületét okozza, és ez a görbület szabja meg a tér-idő utat, amelyet a szabadon eső testeknek követniük kell. Ebből az elmélet következett az az előrejelzés is, hogy a fényre hatással kell lennie a gravitációnak – mindezt sikerült kísérletileg is igazolni. A relativitáselmélet ezen aspektusa megmagyarázta a fény elhajlását a Nap körül, előrejelezte a fekete lyukakat, éppúgy, mint a kozmikus mikrohullámú háttérsugárzás tulajdonságait – amely felfedezés rendezi az alapvető anomáliákat a klasszikus állandósult-állapot hipotézisben. Munkájáért a relativitáselmélet, a fényelektromos jelenség és a feketetest-sugárzás területén Einstein 1921-ben megkapta a Nobel-díjat.
A relativitásról és a fényátvitel kvantált természetéről megfogalmazott Einstein-elméletek fokozatos elfogadása, és a Niels Bohr-féle atommodell legalább annyi problémát hozott létre, mint amennyit megoldott, ez vezetett el ahhoz a nagyméretű erőfeszítéshez, hogy a fizikát az új alapelvekre helyezzék. A relativitáselmélet 1910-es kiterjesztésével a gyorsuló vonatkozási rendszerekre (az „általános relativitáselmélet”) Einstein egyenlőségjelet tett a gyorsulás tehetetlenségi ereje és a gravitációs erő közé, elvezetve ahhoz a következtetéshez, hogy a tér görbült és méretében véges, valamint az olyan jelenségek előrejelzéséhez, mint a gravitációs lencse és az idő torzulása a gravitációs mezőkben.
Kvantummechanika[szerkesztés]

Bár a relativitáselmélet feloldotta az elektromágneses jelenség Michelson és Morley által bemutatott ellentétét, egy másik elméleti probléma volt a feketetest által kibocsátott elektromágneses sugárzás eloszlásának a magyarázata; a kísérlet azt mutatta, hogy rövidebb hullámhosszok esetén, a spektrum ultraibolya vége felé, az energia közelített a nullához, de a klasszikus elmélet előrejelzése az volt, hogy végtelenné kell válnia. Ezt az ultraibolya katasztrófaként ismert jelentős ellentmondást a kvantummechanika új elméletével sikerült feloldani. A kvantummechanika az atomok és szubatomi rendszerek elmélete. Körülbelül a 20. század első 30 éve jelenti az elmélet megfoganásának és kifejlődésének időszakát. A kvantumelmélet alapvető gondolatait 1900-ban Max Planck (1858–1947) mutatta be, aki az energia kvantifikált jellegével kapcsolatos felfedezéséért 1918-ban megkapta a fizikai Nobel-díjat. A kvantumelmélet (amely korábban az atom kvantált világa és a „klasszikus” világ folytonosságai közti „hasonlóságokra” támaszkodott) akkor lett elfogadott, amikor a Compton-hatás kimutatta, hogy a fénynek impulzusa van, valamint részecskéket tud szétszórni, és amikor Louis de Broglie megerősítette, hogy az anyag hullámként való viselkedése éppúgy megfigyelhető, mint az elektromágneses hullámok részecskeviselkedése (hullám-részecske kettősség).

1905-ben Einstein a kvantumelméletet használta a fényelektromos jelenség magyarázatánál, és 1913-ban Niels Bohr dán fizikus ugyanazt az állandót használta, hogy megmagyarázza a Rutherford-atom stabilitását és a hidrogéngáz által kibocsátott fény frekvenciáit. Az atom kvantált elmélete az 1920-as években utat nyitott a nagy léptékű kvantummechanikának. A „klasszikus”-hoz képest a „kvantum”-mechanika új elvei, melyeket 1925-ben Werner Heisenberg, Max Born és Pascual Jordan fejezett ki mátrix alakban, inkább a diszkrét „állapotok” közti valószínűségi összefüggésen alapultak, és elutasították a kauzalitás lehetőségét. A kvantummechanika alapos kidolgozása Heisenberg, Wolfgang Pauli, Paul Dirac és Erwin Schrödinger nevéhez fűződik, aki 1926-ban egy hullámokon alapuló ekvivalens elméletet alakított ki, de Heisenberg 1927-es „határozatlansági elve” (amely a hely és a lendület pontos és egyidejű mérésének a lehetetlenségét jelzi) és a kvantummechanika „koppenhágai értelmezése” (Bohr városa után elnevezve) továbbra is tagadta az alapvető kauzalitás lehetőségét, bár ellenzői, mint Einstein, metaforikusan azt állították, „Isten nem kockázik a világegyetemmel”.[46] Az új kvantummechanika az atomi szintű jelenségek vizsgálatának és magyarázatának nélkülözhetetlen eszközévé vált. Szintén az 1920-as években Satyendra Nath Bose indiai fizikus munkássága a fotonok és a kvantummechanika kapcsán szolgáltatta az alapot a Bose–Einstein-statisztikához, a Bose–Einstein-kondenzáció elméletéhez.
A spin-statisztika tétel megállapította, hogy a kvantummechanikában bármely részecske vagy egy bozon (statisztikailag Bose–Einstein), vagy egy fermion (statisztikailag Fermi–Dirac) lehet. Később derült ki, hogy az összes alapvető bozon erőt közvetít, mint például a foton, amely az elektromágnesességet közvetíti.
A fermionok „az elektronokhoz és nukleonokhoz hasonlatos” részecskék, és az anyag szokásos alkotóelemei. A Fermi–Dirac-statisztika később számos egyéb területen is felhasználásra került, az asztrofizikától (ld. degenerált anyag) a félvezetőtervezésig.
Kortárs és részecskefizika[szerkesztés]
Kvantum mezőelmélet[szerkesztés]
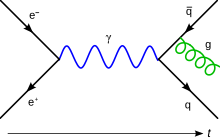

Mialatt a filozofikus hajlamúak tovább elmélkedtek a világegyetem alapvető természetéről, további kvantumelméletek keletkeztek, kezdve Paul Dirac megfogalmazásával egy relativisztikus kvantumelmélet kapcsán 1928-ban. Azonban az elektromágneses elméletek teljes mértékű kvantálásának a kísérleteit az 1930-as évek folyamán megakasztották a végtelen energiákat nyerő elméletek megfogalmazásai. Ezt a helyzetet nem tekinthették megfelelően megoldottnak a második világháború vége utánig, amikor Julian Schwinger, Richard Feynman és Sin-Itiro Tomonaga egymástól függetlenül rögzítették a renormalizáció technikáját, mely lehetővé tette egy robusztus kvantum-elektrodinamika (QED) kialakítását.[47]
Mindeközben a rövid életű „virtuális” részecskék kicserélődése által szabályzott „kicserélődési erőkön” keresztüli mezőkvantizációs gondolat felemelkedésével virágkorukat élték az alapvető részecskék új elméletei, ezen részecskék létezése megengedett a kvantumvilágban rejlő bizonytalanságokat szabályzó törvények alapján. Jelentőségteljes volt Jukava Hideki javaslata, miszerint a mag pozitív töltései egy erős, de rövid hatótávolságú erőnek köszönhetően maradnak együtt, amit egy olyan részecske közvetít, melynek tömege az elektron és a proton tömege közé esik. Ezt a részecskét, a „piont” a második világháború után felfedezett rengeteg részecske egyikeként 1947-ben azonosították. Kezdetben ilyen részecskéket a kozmikus sugárzásból visszamaradt ionizáló sugárzásként találták meg, de egyre növekvő számban sikerült őket előállítani az újabb és erősebb részecskegyorsítókban.[48]
A részecskefizikán kívül az adott időszak jelentős fejleményei voltak:
- a lézer feltalálása (1964-es fizikai Nobel-díj);
- a szupravezetés elméleti és kísérleti kutatása, különösen a szupravezetés kvantumelméletének a feltalálása (Vitalij Ginzburg és Lev Landau, 1962-es fizikai Nobel-díj), és később magyarázata a Cooper-párokon keresztül (1972-es fizikai Nobel-díj). A Cooper-pár a kvázirészecskék egy korai példája volt.
Egységes mezőelméletek[szerkesztés]
Einstein úgy vélte, hogy a természetben minden alapvető kölcsönhatás megmagyarázható egyetlen elmélettel. Az egységes mezőelméletek a különböző kölcsönhatások „összevonásának” számos próbálkozása volt. Ilyen elméletek egyik (és vele együtt a mezőelméletek általános) megfogalmazása a mértékelmélet, a szimmetria elképzelésének egyik általánosítása. Tulajdonképpen a standard modell lett sikeres az erős, gyenge és elektromágneses kölcsönhatások egyesítésében. Minden próbálkozás a gravitáció egyesítésére valami mással kudarcot vallott.
Standard modell[szerkesztés]

Ezen részecskék szórás és bomlás általi kölcsönhatása szolgáltatta a kulcsot az új alapvető kvantumelméletekhez. Murray Gell-Mann és Júval Neemán valamiféle rendet vitt ezen új részecskék közé, bizonyos minőségeiken alapuló osztályzással, kezdve a Gell-Mann által hivatkozott „nyolc helyes úttal”. Míg további fejlődése, a kvarkmodell elsőre nem tűnt megfelelőnek az erős magerők leírására, teret engedve az olyan versengő elméletek ideiglenes felemelkedésének, mint az S-mátrix, a kvantum-színdinamika kialakulása az 1970-es években véglegesítette az alapvető és kicserélődési részecskék készletét, mely lehetővé tette egy „standard modell” kialakítását a mértékinvariancia matematikájára alapozva, ez pedig sikeresen leírta az összes erőt a gravitáció kivételével, és amely továbbra is általánosan elfogadott alkalmazásának területén.[46]
A standard modell az elektrogyenge kölcsönhatást és a kvantum-színdinamikát egy SU(3)×SU(2)×U(1) mértékcsoporttal jelölt struktúrába csoportosítja. A standard modellben az elektromágneses és a gyenge kölcsönhatás egységesítésének leírása Abdus Salamnak, Steven Weinbergnek és később Sheldon Glashow-nak köszönhető. Az elektrogyenge kölcsönhatás később kísérleti úton megerősítést nyert (a semleges gyenge áramok megfigyelésével),[49][50][51][52] és ezt ismerte el az 1979-es fizikai Nobel-díj.[53]
Az 1970-es évek óta az alapvető részecskék fizikája betekintést nyújtott a korai világegyetem kozmológiájába, elsősorban a ősrobbanás elméletének felvetésével, mint Einstein általános relativitáselméletének egyik következménye. Azonban az 1990-es évektől kezdve a csillagászati megfigyelések új kihívásokat szolgáltattak, mint például a galaktikus stabilitás („sötét anyag”) és a világegyetem tágulásának nyilvánvaló gyorsulása („sötét energia”) új magyarázatainak a szükségessége.
Míg a gyorsítók a különböző ütközési energiákon a várt részecske kölcsönhatások érzékelésével a standard modell legtöbb aspektusát megerősítették, az általános relativitáselmélet összeegyeztetését a standard modellel még nem sikerült megtalálni, habár a szuperszimmetriát és a húrelméletet sok elméleti fizikus egy ígéretes előrevezető útnak hitte. A Nagy Hadronütköztető azonban, mely 2008-ban kezdett el üzemelni, kudarcot vallott bármilyen olyan bizonyíték megtalálásában, amely a szuperszimmetriát és a húrelméletet alátámasztaná.[54]
Kozmológia[szerkesztés]
Elmondható, hogy Einstein általános relativitáselméletének kiadásával 1915-ben a kozmológia egy komoly kutatási kérdéssé vált, bár az „általános relativitáselmélet aranykora” néven ismert időszakig nem volt része a fő tudományos irányvonalaknak.
Körülbelül egy évtizeddel később, a Nagy Vita közepén, az 1920-as években Hubble és Slipher, megmérve a galaktikus ködök Doppler-spektrumainak vöröseltolódását, felfedezte a világegyetem tágulását. Felhasználva Einstein általános relativitáselméletét Lemaître és Gamow megfogalmazta a később ősrobbanásként ismertté vált elméletet. Egy rivális, állandósult állapotnak nevezett elméletet vezetett le Hoyle, Gold, Narlikar és Bondi.
A kozmikus háttérsugárzást az 1960-as években Penzias és Wilson igazolta, és ez a felfedezés az ősrobbanásnak kedvezett az állandósult állapot forgatókönyvének kárára. A Cosmic Background Explorer (CoBE) és a Wilkinson Microwave Anisotropy Probe (WMAP) adatait felhasználva egy későbbi munka, más közreműködőkkel együtt, Smoothoz és társaihoz (1989) köthető, amely finomította ezeket a megfigyeléseket. Az 1980-as években (a COBE méréseivel azonos évtizedben) látott napvilágot Guth javaslata a felfúvódási elméletről.
Mostanában a sötét anyag és a sötét energia problémái emelkedtek a kozmológia napirendjének az élére.
Higgs-bozon[szerkesztés]

2012. július 4-én a CERN Nagy Hadronütköztetőjében dolgozó fizikusok bejelentették, hogy egy Higgs-bozonra nagyban hasonlító, új szubatomi részecskét fedeztek fel, egy lehetséges kulcsot annak a megértéséhez, miért van az elemi részecskéknek tömegük, és valójában a világegyetembeli sokféleség és élet létezésének lehetséges kulcsát.[55] Egyelőre egyes fizikusok ezt egy „Higgs-szerű” részecskének nevezik.[55] Joe Incandela a Santa Barbara-i Kaliforniai Egyetemről azt mondta: „Ez olyasmi, ami végül a mi területünkön felbukkant új jelenségek egyik legnagyobb megfigyelése lehet az utóbbi 30 vagy 40 évben, visszamenőleg egészen például a kvarkok felfedezéséig.”[55] Michael Turner, a Chicagói Egyetem kozmológusa és a fizikai központ tanácsának az elnöke szerint:
| „Ez egy nagy pillanat a részecskefizika számára, és egy válaszút – ez lesz vajon a legmagasabb szint, vagy első lesz a sok felfedezés közül, ami azon igazán nagy kérdés megoldása felé vezet minket, amit feltettünk?” | |
– Michael Turner, Chicagói Egyetem[55]
|
Peter Higgs egyike volt annak a három független csoportban dolgozó hat fizikusnak, akik 1964-ben kitalálták a Higgs-mező („kozmikus melasz”) fogalmát. A többi fizikus Tom Kibble a londoni Imperial College-ről; Carl Hagen a Rochesteri Egyetemről; Gerald Guralnik a Brown Egyetemről; valamint François Englert és Robert Brout az Université libre de Bruxelles-ről voltak.[55]
Bár soha nem voltak láthatók, a Higgs-szerű mezők fontos szerepet játszanak a világegyetem elméletében és a húrelméletben. Bizonyos feltételek esetén az einsteini fizika furcsa jelentése szerint olyan energiával elárasztottakká válhatnak, amely antigravitációs hatást gyakorol. Az ilyen mezőket javasolták a világegyetem korai szakaszában a felfúvódásként ismert hatalmas tágulási löketek forrásaként, és feltehetően a sötét energia titkaként, ami jelenleg úgy tűnik, gyorsítja a világegyetem tágulását.[55]
Fizikai tudományok[szerkesztés]
A 19. században a fejlettebb analitikai technikákhoz való szélesebb hozzáféréssel és kidolgozottsággal a fizikát épp annyira, ha nem jobban ezek a technikák határozták meg, mint a mozgás és energia egyetemes elveinek, és az anyag alapvető természetének a keresése. Az olyan területek, mint a hangtan, a geofizika, az asztrofizika, az aerodinamika, a plazmafizika, az alacsony hőmérsékletű fizika és a szilárdtestfizika csatlakoztak a fénytanhoz, a folyadékdinamikához, az elektromágnesességhez és a mechanikához mint a fizikai kutatás területei. A 20. században a fizika közeli szövetségbe került az olyan területekkel is, mint a villamos-, repülő- és anyagtudományi mérnökség, és a fizikusok elkezdtek éppannyira kormányzati és ipari laboratóriumokban dolgozni, mint akadémiai műhelyekben. A második világháború után a fizikusok népszerűsége drámaian megnőtt, és az Egyesült Államokba központosultak, míg az újabb évtizedekben a fizika még nemzetközibb tevékenységgé vált, mint valaha is korábbi történetében.
Alapvető fizikai kiadványok[szerkesztés]
| Szerző | Élt | Hozzájárulás | |
|---|---|---|---|
| Arisztotelész | i. e. 384 – 322 | Physicae Auscultationes | |
| Arkhimédész | i. e. 287 – 212 | Az úszó testekről | |
| Ptolemaiosz | 90 – 168 | ||
| Alhazen | 965 – 1040 | A fénytan könyve | |
| Kopernikusz | 1473 – 1543 | Az égi pályák körforgásairól | 1543 |
| Galilei | 1564 – 1642 | Párbeszédek a két legnagyobb világrendszerről | 1632 |
| Descartes | 1596 –1650 | Elmélkedések az első filozófiáról | 1641 |
| Newton | 1643 – 1727 | Philosophiae Naturalis Principia Mathematica | 1687 |
| Faraday | 1791 – 1867 | Az elektromosság kísérleti vizsgálata | 1839 / 1844 |
| Maxwell | 1831 – 1879 | Értekezés az elektromosságról és a mágnesességről | 1873 |
| Einstein | 1879 – 1955 | Annus Mirabilis dolgozatok | 1905 |
Megjegyzések[szerkesztés]
- ↑ Rāshid, Rushdī. Encyclopedia of the history of Arabic science. London New York: Routledge, 614-642. o. (1996). ISBN 0-415-12410-7:
„A matematikai módszerek egész garmadát használva (és nem csak az ókori elméletekből örökölt törteket és infinitezimális technikákat, hanem a kortárs algebra módszereit és finom számítási technikáit is), az iszlám tudósok a statikát egy új, magasabb szintre emelték. Arkhimédész klasszikus eredményei a gravitációs középpont elméletéből általánosításra kerültek és alkalmazták őket a három dimenziós testekre, lefektették a mérlegemelő elméletének alapjait, és a megszületett a 'gravitáció tudománya', ami a középkori Európában fejlődött majd tovább. A statika jelenségeit dinamikus megközelítésben tanulmányozták, így kiderült, hogy a két irányzat - a statikus és dinamikus - kölcsönös kapcsolatban van egy külön tudományon, a mechanikán belül. A dinamikus megközelítés kombinációja az arkhimédészi hidrosztatikával életet adott a tudományon belül egy irányzatnak, amit talán középkori áramlástannak is hívhatunk.
Az arkhimédészi statikáján álltak a jellemző súly tudományának alapjai. Számos finom kísérleti módszert fejlesztettek ki egy bizonyos súly meghatározására, amelyek különösen az egyensúlyok és mérés elméletére épültek. Al-Biruni és al-Khazini klasszikus művei jogosan tekinthetők a középkori tudományban a kísérleti módszerek alkalmazásának kezdetének.
Az arab statika lényeges kapocs volt a világ tudományának fejlődésében. Fontos szerepet játszott a középkori Európában a klasszikus mechanika előtörténetében. Nélküle a klasszikus mechanika valószínűleg szó szerint nem jöhetett volna létre.”
Hivatkozások[szerkesztés]
- ↑ Levél Robert Hooke-hoz (1676. február 15. gregoriánus számítás szerint január 1-i Újévvel, megfelel 1675. február 5-ének a julián naptár szerint március 25-i Újévvel)
- ↑ "Ez az eltolódás az egyházi magyarázatoktól a tudományosak felé jelezte a tudományos módszertan kezdetét." Singer, C., A Short History of Science to the 19th Century, Streeter Press, 2008, p. 35.
- ↑ Eratosthenes and the Mystery of the Stades - How Long Is a Stade? | Mathematical Association of America. www.maa.org. (Hozzáférés: 2016. november 7.)
- ↑ Leaman, Oliver. Key concepts in Eastern philosophy. London New York: Routledge, 269. o. (1999). ISBN 978-0-415-17363-6
- ↑ Radhakrishnan, Sarvepalli. Indian philosophy. New Delhi Oxford: Oxford University Press, 202. o. (2008). ISBN 978-0-19-569841-1
- ↑ Chtcherbatskoï, Fedor. 1, Buddhist logic. New York: Dover Publications, 19. o. (1962). ISBN 978-0-486-20955-5
- ↑ Li Shu-hua, "Origine de la Boussole 11. Aimant et Boussole", Isis, Vol. 45, No. 2. (Jul., 1954), p. 175
- ↑ Needham, Joseph. Part 1, Physics, Science and Civilisation in China – Volume 4, Physics and Physical Technology. Cambridge England: University Press (1954). ISBN 978-0-521-05802-5
- ↑ szerk.: Robinson, Francis: The Cambridge Illustrated History of the Islamic World. Cambridge University Press, 228–229. o. (1996)
- ↑ Glick, Thomas. Medieval science, technology, and medicine : an encyclopedia. New York: Routledge, 89-90. o. (2005). ISBN 0-415-96930-1
- ↑ Top 10 ancient Arabic scientists. COSMOS magazine, 2011. január 6. (Hozzáférés: 2016. november 11.)
- ↑ Crombie, A. C. (1961). „Quantification in Medieval Physics”. Isis 52 (2), 143–160. o, Kiadó: University of Chicago Press. DOI:10.1086/349467. (Hozzáférés: 2016. november 11.)
- ↑ Lindberg, David. The beginnings of western science : the European scientific tradition in philosophical, religious, and institutional context, prehistory to A.D. 1450. Chicago: University of Chicago Press (2007). ISBN 978-0-226-48205-7
- ↑ GALILEI: PÁRBESZÉDEK. mek.oszk.hu. (Hozzáférés: 2016. november 11.)
- ↑ Drake, Stillman. Galileo at work : his scientific biography. Chicago: University of Chicago Press (1978). ISBN 0-226-16226-5
- ↑ Biagioli, Mario. Galileo, courtier : the practice of science in the culture of absolutism. Chicago: University of Chicago Press (1993). ISBN 0-226-04559-5
- ↑ Charles Singer (1942). „A Short History of Science to the Nineteenth Century”. Science Education 26 (2), 217. o, Kiadó: Wiley-Blackwell. DOI:10.1002/sce.3730260220. (Hozzáférés: 2016. november 11.)
- ↑ a b Weidhorn, Manfred. The person of the millennium : the unique impact of Galileo on world history. New York Lincoln, NE: iUniverse (2005). ISBN 0-595-36877-8
- ↑ Stephen Hawking, "Galileo and the Birth of Modern Science", American Heritage's Invention & Technology, Vol. 24, No. 1 (Spring 2009), p. 36.
- ↑ (Shea 1991)
- ↑ (Garber 1992)
- ↑ (Gaukroger 2002)
- ↑ (Hall 1980)
- ↑ (Bertolini Meli 1993)
- ↑ a b (Guicciardini 1999)
- ↑ The Early Period (1608–1672). James R. Graham (webpage). (Hozzáférés: 2009. február 3.)[halott link]
- ↑ Błaszczyk, Piotr; Katz, Mikhail & Sherry, David (2012), "Ten misconceptions from the history of analysis and their debunking", Foundations of Science, DOI 10.1007/s10699-012-9285-8
- ↑ New Experiments physico-mechanicall, Touching the Spring of the Air and its Effects (1660). [1]
- ↑ (Darrigol 2005)
- ↑ (Bos 1980)
- ↑ (Heilbron 1979)
- ↑ (Buchwald 1989)
- ↑ (Golinski 1999)
- ↑ (Greenberg 1986)
- ↑ (Guicciardini 1989)
- ↑ (Garber 1999)
- ↑ (Ben-Chaim 2004)
- ↑ (Buchwald 1985)
- ↑ (JungnickelMcCormmanch 1986)
- ↑ (Hunt 1991)
- ↑ (Buchwald 1994)
- ↑ Michael Windelspecht, Groundbreaking Scientific Experiments, Inventions, and Discoveries of the 19th Century, Greenwood Publishing Group, 2003 page 195
- ↑ (Smith & Wise 1989)
- ↑ (Smith 1998)
- ↑ (Agar 2012)
- ↑ a b (Kragh 1999)
- ↑ (Schweber 1994)
- ↑ (Galison 1997)
- ↑ F. J. Hasert et al. Phys. Lett. 46B 121 (1973).
- ↑ F. J. Hasert et al. Phys. Lett. 46B 138 (1973).
- ↑ F. J. Hasert et al. Nucl. Phys. B73 1(1974).
- ↑ The discovery of the weak neutral currents, CERN courier, 2004-10-04, <http://cerncourier.com/cws/article/cern/29168>. Hozzáférés ideje: 2008-05-08
- ↑ The Nobel Prize in Physics 1979, Nobel Foundation, <http://www.nobel.se/physics/laureates/1979>. Hozzáférés ideje: 2008-09-10
- ↑ Woit, Peter: Last Links For a While. Not Even Wrong, 2013. október 20. (Hozzáférés: 2013. november 2.)
- ↑ a b c d e f Overbye, Dennis. „Physicists Find Particle That Could Be the Higgs Boson”, The New York Times, 2012. július 4.
Fordítás[szerkesztés]
- Ez a szócikk részben vagy egészben a History of physics című angol Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.
Források[szerkesztés]
- Agar, Jon. Science in the Twentieth Century and Beyond. Polity Press (2012). ISBN 978-0-7456-3469-2.
- Arisztotelész Fiziká-ja Hardie & Gaye fordításában
- Ben-Chaim, Michael. Experimental Philosophy and the Birth of Empirical Science: Boyle, Locke and Newton. Ashgate (2004). ISBN 0-7546-4091-4. OCLC 53887772.
- Bertolini Meli, Domenico. Equivalence and Priority: Newton versus Leibniz. Oxford University Press (1993).
- Biagioli, Mario. Galileo, Courtier: The Practice of Science in the Culture of Absolutism. University of Chicago Press (1993). ISBN 0-226-04559-5. OCLC 185632037.
- Bos, Henk. The Ferment of Knowledge: Studies in the Historiography of Eighteenth Century Science. Cambridge University Press (1980).
- Buchwald, Jed. From Maxwell to Microphysics: Aspects of Electromagnetic Theory in the Last Quarter of the Nineteenth Century. University of Chicago Press (1985). ISBN 0-226-07882-5. OCLC 11916470.
- Buchwald, Jed. The Rise of the Wave Theory of Light: Optical Theory and Experiment in the Early Nineteenth Century. University of Chicago Press (1989). ISBN 0-226-07886-8. OCLC 18069573.
- Buchwald, Jed. The Creation of Scientific Effects: Heinrich Hertz and Electric Waves. University of Chicago Press (1994). ISBN 0-226-07888-4. OCLC 29256963.
- Chattopadhyaya. {{{title}}} (1986)
- Darrigol, Olivier. Worlds of Flow: A History of Hydrodynamics from the Bernoullis to Prandtl. Oxford University Press (2005). ISBN 0-19-856843-6. OCLC 237027708.
- Drake, Stillman. Galileo at Work: His Scientific Biography. University of Chicago Press (1978). ISBN 0-226-16226-5. OCLC 185633608.
- Galison, Peter. Image and Logic: A Material Culture of Microphysics. University of Chicago Press (1997). ISBN 0-226-27917-0. OCLC 174870621.
- Garber, Daniel. Descartes' Metaphysical Physics. University of Chicago Press (1992).
- Garber, Elizabeth. The Language of Physics: The Calculus and the Development of Theoretical Physics in Europe, 1750–1914. Birkhäuser Verlag (1999).
- Gaukroger, Stephen. Descartes' System of Natural Philosophy. Cambridge University Press (2002).
- Medieval Science, Technology, and Medicine: An Encyclopedia. Routledge (2005). ISBN 0-415-96930-1. OCLC 218847614
- Greenberg, John. Mathematical Physics in Eighteenth-Century France, 59–78. o.. DOI: 10.1086/354039 (1986).
- Golinski, Jan. Science as Public Culture: Chemistry and Enlightenment in Britain, 1760–1820. Cambridge University Press (1999).
- Guicciardini, Niccolò. The Development of Newtonian Calculus in Britain, 1700–1800. Cambridge University Press (1989).
- Guicciardini, Niccolò. Reading the Principia: The Debate on Newton's Methods for Natural Philosophy from 1687 to 1736. Cambridge University Press (1999).
- Hall, A. Rupert. Philosophers at War: The Quarrel between Newton and Leibniz. Cambridge University Press (1980).
- Heilbron, J. L.. Electricity in the 17th and 18th Centuries. University of California Press (1979).
- Hunt, Bruce. The Maxwellians. Cornell University Press (1991).
- Intellectual Mastery of Nature: Theoretical Physics from Ohm to Einstein. University of Chicago Press (1986).
- Kragh, Helge. Quantum Generations: A History of Physics in the Twentieth Century. Princeton University Press (1999).
- Radhakrishnan. {{{title}}} (2006)
- Schweber, Silvan. QED and the Men Who Made It: Dyson, Feynman, Schwinger, and Tomonaga. Princeton University Press (1994).
- Shea, William. The Magic of Numbers and Motion: The Scientific Career of René Descartes. Science History Publications (1991).
- Smith, Crosbie. The Science of Energy: A Cultural History of Energy Physics in Victorian Britain. University of Chicago Press (1998).
- Energy and Empire: A Biographical Study of Lord Kelvin. Cambridge University Press (1989).
További információk[szerkesztés]
- Buchwald, Jed Z. and Robert Fox, eds. The Oxford Handbook of the History of Physics (2014) 976pp; részlet
- Out of the Shadows: Contributions of Twentieth-Century Women to Physics. Cambridge University Press (2006). ISBN 0-521-82197-5
- Cropper, William H.. Great Physicists: The Life and Times of Leading Physicists from Galileo to Hawking. Oxford University Press (2004). ISBN 0-19-517324-4
- Dear, Peter. Revolutionizing the Sciences: European Knowledge and Its Ambitions, 1500–1700. Princeton University Press (2001). ISBN 0-691-08859-4. OCLC 46622656.
- Gamow, George. The Great Physicists from Galileo to Einstein. Dover Publications (1988). ISBN 0-486-25767-3
- Heilbron, John L.. The Oxford Guide to the History of Physics and Astronomy. Oxford University Press (2005). ISBN 0-19-517198-5
- Nye, Mary Jo. Before Big Science: The Pursuit of Modern Chemistry and Physics, 1800–1940. Twayne (1996). ISBN 0-8057-9512-X. OCLC 185866968.
- Segrè, Emilio. From Falling Bodies to Radio Waves: Classical Physicists and Their Discoveries. W. H. Freeman (1984). ISBN 0-7167-1482-5. OCLC 9943504.
- Segrè, Emilio. From X-Rays to Quarks: Modern Physicists and Their Discoveries. W. H. Freeman (1980). ISBN 0-7167-1147-8. OCLC 237246197.
- Weaver, Jefferson H. (editor). The World of Physics. Simon and Schuster (1987). ISBN 0-671-49931-9 Egy 56 cikkből álló, fizikusok által írt válogatás. Megjegyzésekkel és jegyzetekkel ellátta Lloyd Motz és Dale McAdoo.
- de Haas, Paul, "Historic Papers in Physics (20th Century)"
- "Selected Works about Isaac Newton and His Thought" a The Newton Project[halott link]-ből.
Magyar nyelvű szakirodalom[szerkesztés]
- Baumgartner Alajos: A fizika története, Budapest, Stampfel-féle Könyvkiadóhivatal, 1913
- Bernal, J. D.: A fizika fejlődése Einsteinig, Gondolat Kiadó–Kossuth Kiadó, 1977
- Czógler Alajos: A fizika története életrajzokban I–II., Budapest, Királyi Magyar Természettudományi Társulat, 1882
- Fehér Imre – Horváth Árpád: A fizika és a haladás I–IV., Budapest, Tankönyvkiadó, 1960–1967
- Fülöp Zsigmond: A kísérletezés úttörői, Budapest, Gondolat Kiadó, 1958
- Gamow, George: A fizika története, Budapest, Gondolat Könyvkiadó, 1965
- Gazda István – Sain Márton: Fizikatörténeti ABC, Budapest, Tankönyvkiadó, 1980
- Heller Ágost: A physika története I–II., Budapest, Királyi Magyar Természettudományi Társulat, 1891–1902
- Herneck, Friedrich: Az atomkorszak úttörői, Budapest, Gondolat Kiadó, 1969
- Koczkás Gyula: Örök törvények. A fizika regénye, Budapest, Béta Irodalmi Rt., 1947
- Komjáthy Aladár: A tudás fája. Természetmagyarázat az ókortól napjainkig, Budapest, Egyetemi Nyomda, 1947
- Kudrjavcev, P. Sz.: A fizika története, Budapest, Akadémiai Kiadó, 1960
- Laue, Max von.: A fizika története, Budapest, Gondolat Kiadó, 1960
- Molnár Miklós: A fizika története, Szeged, JATE Kiadó, 1990
- Szabó Árpád: A fizika története, Budapest, Akadémiai Kiadó, 2007
- Simonyi Károly: A fizika kultúrtörténete, Budapest, Gondolat Könyvkiadó, 1978
- M. Zemplén Jolán: A háromezeréves fizika, Budapest, Akadémiai Kiadó, 1961
- M. Zemplén Jolán: A magyarországi fizika története 1711-ig, Budapest, Akadémiai Kiadó, 1961
- M. Zemplén Jolán: A magyarországi fizika története a XVIII. században, Budapest, Akadémiai Kiadó, 1964
