Optika

Az optika, vagy magyarosan fénytan, a fizikának a fény és általában az elektromágneses hullámok terjedésével foglalkozó tudományága. A fénytan (optika) a fény tulajdonságait, a fényjelenségeket (fénytörés, fényvisszaverődés stb.) vizsgálja.

Főbb megközelítési módjai:

• a geometriai optika, amely a fényt mint egy sugarat tekinti, mely egyenes vonalban halad az egyes közegekben, közeghatárokon pedig visszaverődik vagy megtörik
• a hullámoptika, amely a fényt hullámként modellezi. Így magyarázható a fényelhajlás, az interferencia és a polarizáció jelensége;
• a kvantumoptika, amely vékony rétegek és határjelenségek magyarázatára szolgál

Mindegyik magában foglalja az előző lépcsőfokot.

A fény színe

Olyan fiziológiai érzet, amelyet a látható optikai sugárzás kelt, méghozzá a hullámhosszától függő minőségben.

Színek	Hullámhossz vákuumban (nm)	Frekvencia (Hz)
Infravörös	$700$	$4,3 \cdot 10^{14}$
Vörös	$620$	$4,8 \cdot 10^{14}$
Narancs	$610$	$4,9 \cdot 10^{14}$
Sárga	$590$	$5,1 \cdot 10^{14}$
Zöld	$510$	$5,9 \cdot 10^{14}$
Kék	$430$	$6,9 \cdot 10^{14}$
Ibolya	$400$	$7,5 \cdot 10^{14}$
Ultraibolya	$300$	$5 \cdot 10^{15}$

Színkép vagy spektrum

Valamely fényforrás hullámhossz szerint felbontott fényében a színekhez tartozó intenzitás frekvenciára való eloszlását leíró függvény, illetve a fényspektrográfok által térben hullámhossz szerint szétbontott képe.

Emissziós színkép

A gerjesztett atomi vagy molekuláris rendszer által kibocsátott elektromágneses hullámok hullámhossz szerinti rendszere.

Folytonos színkép

Olyan emissziós színkép, amelynek az intenzitása a frekvencia folytonos függvénye, és széles tartományban különbözik nullától.

Fényforrások

Meg kell említenünk a fényforrásokat is, mert fényforrás nélkül nincs fény. Két fajta fényforrást különböztetünk meg, az elsődleges és a másodlagos fényforrásokat.

Elsődleges fényforrás

Elsődleges vagy valódi fényforrásnak tekintjük azokat a tárgyakat, amelyek fényt sugároznak, bocsátanak ki. Elsődleges fényforrások: a Nap, a csillagok, a gyertya lángja stb.

Másodlagos fényforrások

Minden test, ami csak a rá sugárzott és róla visszaverődő fény miatt látható, másodlagos fényforrás, mert ha nem verné vissza a fényt, nem látnánk. Tehát akkor látunk valamit, ha a tárgyról a szemünkbe jut a fény.

Fényjelenségek

Ha a fény két eltérő optikai sűrűségű közeg határára érkezik, akkor egy része visszaverődik, másik része pedig belép az új közegbe. Az új közegben haladó fénysugár általában megtörik. A közegek és a határfelület tulajdonságaitól, valamint a beesés szögétől függ, hogy a fényvisszaverődés vagy a fénytörés az erőteljesebb.

A Huygens-elv

Hullámtörés a Huygens-elv alapján

Christian Huygens holland fizikus és csillagász (1629–1695) dolgozta ki az optikai rendszerek elemzésének hasznos módszerét.

A hullámfront minden pontja elemi gömbhullámok kiindulópontja. Az elemi hullámok a fény sebességével terjednek. Egy későbbi „t” időpontban a hullámfront új helyzetét az elemi hullámok burkolója adja meg.

A Huygens-Fresnel-elv

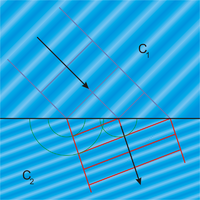
A hullámfront minden pontja elemi gömbhullámok kiindulópontja. Az elemi hullámok a fény sebességével terjednek. Egy későbbi „t” időpontban a hullámfront új helyzetét az elemi hullámok interferenciájának burkolója adja meg.

(Megjegyzés: A hátrafele terjedő elemi hullámok az interferencia miatt kioltódnak.)

Fényvisszaverődés

Hogyha a közegek és a határfelület tulajdonságai úgy hozzák, hogy a visszaverődés erőteljesebb, a jelenséget fényvisszaverődésnek nevezzük.

Teljes visszaverődés (totálreflexió)

Teljes visszaverődés

Ha egy fénysugár az optikailag sűrűbb közeg felől a ritkább közeg felé halad, akkor a határfelületen nem törik meg, hanem azon – mint tökéletes tükrön – visszaverődik. Ilyenkor teljes fényvisszaverődésről vagy más néven totális reflexióról beszélünk, mivel a határfelület a ráeső fény 100%-át visszaveri. A határszöget a törési törvényből könnyedén meghatározhatjuk:

$\frac{{\sin \alpha }}{{\sin 90^\circ }} = \frac{1}{n}$

ebből:

$\sin \alpha _h = \frac{1}{n}$

Brewster törvénye

A visszavert sugár teljesen poláros lesz, ha a visszavert, valamint a közegbe behatoló megtört sugár egymásra merőleges. A teljes polarizációhoz tartozó $\alpha_b$ beesési szög és a törésmutató kapcsolata:

$n = \frac{{\sin \alpha _b }}{{\sin \beta }} = \frac{{\sin \alpha _b }}{{\sin (90^\circ - \alpha _b )}} = \frac{{\sin \alpha _b }}{{\cos \alpha _b }} = tg\alpha _b$

Kísérlet

Fényvisszaverődés sík felületről

Hogy a törvényt ki tudjuk mondani, egy kísérletet kell elvégeznünk, amihez optikai korongot használunk. Az optikai vagy Hartl-korong három részből áll:

• beosztásos korong
• szűrő, ami kiszűri a nem megfelelő irányba haladó fénysugarakat
• tartószerkezet, amire tükröket, illetve lencséket rakhatunk

Jelen esetben a tartószerkezetre egy síktükröt raktunk. A képen látszik, hogy merre halad a fénysugár, és elvileg azt látjuk, ami a mellékelt képen látható.

Törvény

A törvény meghatározásához értelmeznünk kell a képet. Az alábbi elnevezéseket használjuk:

• beeső fénysugár (s): a felülethez tartó fénysugár
• visszavert fénysugár (s’): a felülettől távolodó fénysugár
• beesési pont (O): ahol a beeső fénysugár a felületet éri
• beesési merőleges (n): a beesési pontban a felületre állított merőleges
• beesési szög (α): a beeső fénysugárnak a beesési merőlegessel bezárt szöge
• visszaverődési szög (β=α’): a visszavert fénysugárnak a beesési merőlegessel bezárt szöge

A kísérletből megállapíthatjuk a törvényt:

1. A beeső fénysugár, a beesési merőleges és a visszavert fénysugár egy síkban van.
2. A visszaverődési szög egyenlő a beesési szöggel.

Ezt Euklidesz Kr. e. 300 körül már bebizonyította.

Fénytörés

Fénytörés

Fénytörés

Ha egy üvegpohárba vizet öntünk, s rajta átnézve vizsgáljuk a hozzá közel lévő tárgyakat, eltorzult képet látunk. A vízbe helyezett szívószál például megtörtnek látszik, pedig ha kivesszük a vízből, látható, hogy változatlan az alakja. Nem a szívószál törik meg, hanem a fény, amely a vízből érkezik a szemünkbe.

Ha a fénysugár eltérő fénytani sűrűségű anyagok határán átlép, iránya megváltozik. A víz és a levegő határán mindig megtörik a fény, kivéve, ha éppen merőlegesen esik a vízfelületre.

A fény fázissebességének nagysága

Vákuumban:

$c_0 = \frac{1}{{\sqrt {\varepsilon _0 \mu _0 } }} = 299792458\frac{m}{s}$

Szigetelőben:

$c = \frac{1}{{\sqrt {\varepsilon _0 \mu _0 \varepsilon _r \mu _r }}} = \frac{1}{{\sqrt {\varepsilon \mu } }} \approx \frac{1}{{\sqrt {\varepsilon _0 \mu _0 \varepsilon _r } }} = \frac{{c_0 }}{{\sqrt {\varepsilon _r } }} < c_0$

(ugyanis $\mu _r \approx 1$)

A közeg abszolút törésmutatója

$n = \frac{{c_0 }}{c} = \sqrt {\varepsilon _r \mu _r } \approx \sqrt {\varepsilon _r }$

Diszperzió (színszórás)

A prizma fénytörése az eltérő hullámhosszok miatt alakul ki

$\varepsilon _r$ frekvenciafüggése miatt különböző hullámhosszú fénysugarak ugyanabban a közegben különböző sebességgel terjednek. Az új közegben a fényhullámok különböző frekvenciájú komponensei különböző mértékben térnek el a becslési irányhoz képest, azaz szóródnak. Emiatt bontja színeire a különböző frekvenciájú (színű) fények keverékét a prizma.

Relatív törésmutató

A második közeg első közegre viszonyított relatív törésmutatója:

$n_{21} = \frac{{c_1 }}{{c_2 }} = \frac{{n_2 }}{{n_1 }}$

Az első közeg optikailag akkor sűrűbb a második közegnél, ha $n_{21}\!<\!1$, ellenkező esetben a közeg optikailag ritkább. (Az optikai sűrűség nem azonos a mechanikai sűrűséggel).

Snellius-Descartes fénytörési törvénye

Ugyanazon közegben a beesési és törési szög szinuszának aránya állandó és egyenlő az első, ill. második közegben mért terjedési sebességek hányadosával.

$\frac{{\sin \alpha }}{{\sin \beta }} = \frac{{c_1 }}{{c_2 }} = n_{21} = \frac{{n_2 }}{{n_1 }}$

Az $\alpha$ beesési szög növelésével a fény energiájának egyre kisebb hányada jut be az új közegbe.

Optikai eszközök

• Optikai lencse (domború, homorú)
• Tükör (sík, homorú, domború)
• Prizma
• Szem
• Szemüveg és Kontaktlencse
• Optikai távcsövek
  • Galilei-távcső
  • Kepler-távcső
  • Newton-távcső
  • Cassegrain-távcső
  • Ritchey–Chrétien-távcső
• Mikroszkóp
• Fényképezőgép és őse, a camera obscura
• Kamera
• Diavetítő
• Optikai szál

Lásd még

• Fermat-elv
• Fény
• Fényforrás
• Fénysebesség
• Fénytörés
• Fényvisszaverődés
• Geometriai optika
• Prizma
• Spektrum
• Teljes fényvisszaverődés
• Törésmutató
• Visszatükrözés

Külső hivatkozások

• Optika.lap.hu - linkgyűjtemény
• Fizkapu portál FizFotó rovatának optika tárgyú fotói