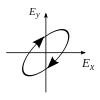Polarizáció
A polarizáció a transzverzális hullámok egy lehetséges tulajdonsága, ami azt jelenti, hogy a rezgés a haladás irányára merőleges, egyetlen síkban zajlik. Egyéb, nem polarizált hullám esetén a rezgések a haladás irányára merőlegesen, minden irányban végbemehetnek.
Mivel a longitudinális hullámoknál a rezgés iránya megegyezik a terjedés irányával, azért a longitudinális hullámok, például a gázokban terjedő hang nem polarizálhatók. Ezzel szemben az elektromágneses hullámok, például a fény transzverzálisak, azaz lehetnek polarizáltak. A longitudinális hullámokhoz hasonlóan a vízfelszíni hullámok rezgésirányának sincs szabadsági foka, nem változtatható meg, ezért nem polarizálhatónak tekintik őket.
Az elektromágneses hullámokban az elektromos és a mágneses mezők is rezegnek, de egymásra és a terjedési irányra is merőlegesek. Megállapodás szerint az elektromos mező rezgésirányát tekintik a polarizáció irányának. A polarizáció lehet lineáris, ami azt jelenti, hogy egy kitüntetett irányban rezeg, de lehet cirkuláris, amikor a rezgés síkja folyamatosan együtt forog a hullám haladásával. Ez az irány lehet az óramutató járása szerinti, vagy azzal ellentétes; ez a polarizáció kezessége vagy kiralitása.
A leggyakoribb optikai anyagok, például az üveg izotropikus, és a rajta áthaladó fény megőrzi polarizációját. Azonban vannak kettős törésű és optikailag aktív anyagok, amelyek a polarizációtól függően másként törik vagy megváltoztatják a fény polarizációját. A lineáris vagy cirkuláris dichroismus esetén az elnyelődés függ a polarizációtól. Erre példa a polarizátor, amelyik csak az egyik irányban polarizált fényt engedi át.
A polarizáció fontos tulajdonság azokon a tudományterületeken, amelyek transzverzális hullámok terjedését vizsgálják. Az optika mellett ilyen a szeizmológia, a rádió- és a mikrohullámok vizsgálata. Különböző technológiáknak is számolniuk kell vele, például a telekommunikációnak, a radarok és a lézerek gyártásának.
A kvantummechanika szerint az elektromágneses hullámok energiája, lineáris és szögmomentuma fotonokként kvantálható. Így megfeleltethető a hullám elektromágneses polarizációja a polarizációs operátoroknak, amelyek meghatározzák annak a valószínűségét, hogy a foton megtalálható-e az adott polarizációs állapotban. Részletesebben, a spin operátor megfeleltethető a cirkuláris polarizáció alapállapotainak, ahogy azt az elektromágneses mezőkkel leírjuk.
A polarizátor olyan eszköz, amely polarizálja a nem polarizált fényt, vagy a fényt a szűrő által meghatározott síkban szűri.
Bevezetés[szerkesztés]

Típusai[szerkesztés]
A polarizációnak alapvetően három típusa van: a lineáris, a cirkuláris és az elliptikus polarizáció.
- Lineáris polarizáció: a kitérés iránya mindig ugyanaz marad, csak a kitérés nagysága és előjele változik. Az irány megadható egy rögzített síkhoz képest, így a függőleges vagy a vízszintes síkhoz viszonyítva vagy párhuzamos (p) és merőleges (s) komponensekként.
- Cirkuláris polarizáció: a kitérés nagysága változatlan, de iránya egyenletes sebességgel körbefordul a terjedés iránya mint tengely körül. Kétféle kezesség avagy kiralitás lehetséges: a jobb (RHCP) és a bal (LHCP), másként az óramutató járása szerinti vagy azzal ellentétes irány.
- Elliptikus polarizáció: a lineáris és a cirkuláris polarizáció keveréke. A kitérés ellipszist ír le.
Elektromágneses hullámok[szerkesztés]
A legtöbb sugárzás a természetben alapvetően polarizálatlan, mivel termikus sugárzásból ered, azonban a szóródás és a visszaverődés miatt részben polarizálódik. A polarizálatlan hullám csak statisztikailag jellemezhető.
A határfelületekről való visszaverődés polarizáció szerint szelektál. Egyes rovarok azért nézik víznek a nagy üvegfelületet és az aszfaltot, mert ugyanolyan arányban ver vissza minden polarizációt, mint a vízfelület. Jellemzően a felülettel párhuzamosan polarizált fény nagyobb arányban lép be, és a rá merőleges nagyobb arányban verődik vissza.
Az ég kékje részben polarizált, mivel szórt fény. A szóródás csak statisztikailag írható le, mert függ a légkör sűrűségingadozásaitól és a molekulák pillanatnyi helyzetétől. A szórási szögtől való függést a Rayleigh-egyenletek írják le.
Látás[szerkesztés]

Számos állatfaj látja a fény polarizációját, vagy legalábbis annak néhány komponensét, például a vízszintes polarizációt. Ezt felhasználják tájékozódásukhoz, mivel az égbolt polarizációja merőleges a Napéra. Ez elterjedt a rovarok között, például a méheknél iránytű a táncok számára,[1] amivel már Karl von Frisch is foglalkozott. Megfigyelték polipoknál, kalmároknál, tintahalaknál,[1] de a legtökéletesebben a sáskarák látja a polarizációt, mivel mind a hat ortogonális orientációt észleli.[2] Például a tintahalak élénk színű, gyorsan változó mintázatok felvételével kommunikálnak, amelyek a polarizációt is kihasználják. A sáskarákoknak polarizációra érzékeny tükröző szövetük van. Népszerű elképzelések szerint a galambok is képesek a polarizáció érzékelésére, de ezt egyes kutatások cáfolták.[3] További fajok a hátonúszó poloska, és a Cataglyphis hangyák.[4][5]
Az ember szabad szemmel gyengén észleli a polarizációt. A polarizált fény hatására egy nagyon halvány mintázat jelenik meg a látótér közepén, amit Haidinger-kefének neveznek. Ezt figyelve gyakorlással rá lehet tanulni a polarizáció látására.[1]
Fizikai háttér[szerkesztés]
Hullámterjedés és polarizáció[szerkesztés]

A legtöbb fényforrás inkoherens és polarizálatlan, mivel sokféle különböző térbeli tulajdonságú, frekvenciájú (színű), fázisú és polarizációjú fényt sugároz ki. Ezzel szemben a polarizáció jobban szemléltethető egy lézersugárral, ami koherens, és adott frekvenciájú. Még jobb, ha síkhullámokat veszünk, amelyek szinuszosak és irányuk, frekvenciájuk, fázisuk és polarizációjuk is egyezik. Ez alapján megmutatható, hogy bármely térbeli szerkezetű hullám felbontható síkhullámok kompozíciójára (szögspektrum). Az inkoherens állapot felfogható úgy is, mint különböző fázisú, polarizációjú és frekvenciájú hullámok keveréke.
Elektromágneses hullámok[szerkesztés]
Az elektromágneses hullámokat általában transzverzálisnak tekintik, ha nem elnyelő, homogén és izotropikus közegben terjednek. Ez azt jelenti, hogy egy síkhullám elektromos mező vektora, E és mágneses vektora, H iránya merőleges a terjedési irányra, és egymásra is. Tekintsünk egy f frekvenciájú, λ vákuumbeli hullámhosszú (f = c/λ) hullámot, és vegyük fel a z tengelyt a terjedés irányába. Így E és H csak x és y irányú komponenseket tartalmaz. Komplex jelöléssel az elektromos és mágneses mezők a következő egyenletekben leírt mennyiségek valós részei. A t idő és z függvényében ezek a komplex mezők ezekkel az egyenletekkel írhatók le:
és
ahol n a közeg törésmutatója, λ/n a közegbeli hullámhossz, és T = 1/f a hullám periódusa. Itt ex, ey, hx, és hy komplex mennyiségek. A második, tömörebb írásmóddal ezeket a tényezőket a hullámszám és az szögfrekvencia fejezi ki. Általánosabban, a terjedés iránya nincs korlátozva, kz-t helyettesíti. Ekkor a hullámvektor, aminek nagysága a hullámszám.
Ezzel az e és a h vezérvektorok két nem nulla komplex komponensből állnak, amelyek a hullám amplitúdóját és frekvenciáját jellemzik. Egy adott η karakterisztikus impedanciájú közegben a h és az e között a következő kapcsolat áll fenn:
és
- .
Dielektrikumokban az η valós, és teljesül rá az η0/n egyenlet, ahol η0 a szabad tér impedanciája. Vezető közegben nem valós komplex értéket vesz fel. A fenti összefüggések alapján E és H skaláris szorzata nulla:
ami azt jelenti, hogy E és H merőlegesek egymásra.
A terjedési irány és η ismeretében meghatározhatjuk az elektromos mezőt jellemző ex és ey komponenseket. A z = 0 komponenst elhagyva ez a Jones-vektor. Az általános Jones-vektor amellett, hogy megadja a hullám polarizáltságát, amplitúdóját és fázisát is meghatározza. Speciálisan, a fény intenzitása arányos az elektromos mező komponensei nagyságának négyzetösszegével:
A polarizáció állapota ezzel szemben csak az ey : ex komplex aránytól függ. Mostantól feltesszük, hogy |ex|2 + |ey|2 = 1. Ez megfelel szabad téren 0,00133 watt/négyzetméter intenzitásnak, ahol . Mivel a hullám abszolút értéke érdektelen a polarizáltság szempontjából, azért feltehetjük azt is, hogy ex fázisa nulla, vagy más szavakkal, exvalós. Ezekkel a feltevésekkel ex és ey reprezentálható, mint:
ahol csak Q jellemzi a polarizációs állapotot, ahol -1 < Q < 1, és a relatív fázis. Megegyezés szerint az elektromágneses hullám polarizáltságát az elektromos mező polarizáltságával jellemezzük. Ehhez képest a mágneses mező polarizáltsága 90 fokkal el van forgatva, ahogy azt a fenti összefüggések is mutatják.
Nem tisztán transzverzális hullámok[szerkesztés]
A fent leírtak mellett még vannak más hullámmozgások is, ahol a rezgések nincsenek korlátozva a terjedésre merőleges irányra. A transzverzális hullámok mellett még azokat az eseteket is figyelembe kell venni, amikor a koherens hullám polarizációja nem írható le egyértelműen a Jones-vektorral. Ez még az elektromágneses hullámokkal is megtörténhet, ha a közeg anizotróp, mint a kettős törésű kristályoknál.
Ezekben az esetekben a D elektromos eltolás és a B mágneses fluxus továbbra is a fenti geometriájú, de az elektromos szuszceptibilitás anizotrópiája miatt E iránya különbözhet D-től, és H iránya különbözhet B-től. Még izotróp közegben is, ha az inhomogén hullámok egy olyan közegbe érkeznek, amelynek komplex törésmutatójának nagy a képzetes része, azaz az elnyelési együtthatója, ezek a mezők nem lesznek szigorúan transzverzálisak.[6]:179–184[7]:51–52
Szabad térben a longitudinális komponensek fókusz régiókban generálhatók, ahol a síkhullám approximáció összeomlik. Extrém példa a radiálisan vagy érintő irányban, polarizált fény, aminek fókuszában az elektromos és a mágneses tér teljesen longitudinális.[8]
Folyadékokban vagy gázokban a hanghullámok longitudinálisak, a polarizáció fel sem merül. Másrészt azonban szilárd testekben transzverzálisak is lehetnek. Ekkor a polarizáció irányát a nyírási feszültség határozza meg, de a terjedés irányára is merőleges. Egy másik komponens, amit longitudinális polarizációnak neveznek, a szilárd test összenyomódását és rezgését írja le a terjedés irányában. A különböző összetevők polarizációja a szeizmológiában fontos.
Polarizációs állapot[szerkesztés]

A polarizáció jobban megérthető, ha először csak tiszta polarizációs állapotokat tekintünk egy bizonyos frekvenciával. A diagramon a vektor egy egy módú lézer által kibocsátott elektromos mező rezgését mutatja, ami azonban 15 nagyságrenddel gyorsabban rezeg. A mező az x-y síkban rezeg, ami megegyezik a lap irányával, és a rezgés a lapra merőleges irányba terjed.
A következő diagramok közül az első kettő lineáris polarizációt jelenít meg. Ezek különböző állapotok, mivel irányuk nem egyezik. A 45 fokos polarizáció felbontható függőleges és vízszintes irányú polarizációra, amelyeknek amplitúdója és fázisa is egyezik. A többi diagram elliptikus polarizációt jelez, ami szintén kifejezhető vízszintes és függőleges irányú összetevőkkel, de most az összetevők között fáziseltolódás van. Ha ez éppen ±90°, akkor a polarizáció cirkuláris. Az eredmény egy forgó elektromos mező. A forgás iránya hozzátartozik a polarizációs állapothoz, így a diagramon ábrázolt két cirkuláris polarizáció különböző.

Az x és az y elemekből álló bázis választása önkényes. Választhatók elliptikus polarizációk is, például a két különböző irányítású kör is. A bázist mindig az adott feladathoz választják a könnyebb kezelhetőség érdekében, például az x vektort a belépés síkjában veszik fel. Mivel a belépés síkjában és rá merőlegesen különbözők a fénytani tulajdonságok, azért ez jelentős könnyebbséget jelent. A körök választása pedig a cirkulárisan polarizált fény kettős törésének, és az optikai aktivitás kezelését könnyíti meg.
Polarizációs ellipszis[szerkesztés]

Tekintsünk egy teljesen polarizált monokromatikus (egységes frekvenciájú) hullámot! Ha felrajzoljuk az elektromos teret, akkor a rezgés egy periódusa alatt egy ellipszist söprünk végig. Jegyezzük meg, hogy a cirkuláris és a lineáris polarizáció az elliptikus polarizáció speciális esete.
A polarizációs állapot leírható az ellipszis geometriai tulajdonságaival, és a körüljárás irányával. Az ellipszis egy lehetséges leírása megadja a ψ irányszöget, ami az x tengely és a nagytengely által bezárt szög,[9] valamint az ε=a/b elliptikusságot, azaz a kis- és a nagytengely arányát.[10][11][12][13] Az ellipszis alakjának jellemzésére az excentricitás is használható, vagy a χ = arctan b/a= arctan 1/ε elliptikussági szög.[9] A χ szög a polarizációs állapotot jellemző Poincaré-gömbön is megjelenik, ahol a polarizációs állapot szélessége ±2χ. A lineáris állapotok elliptikussága végtelen, a cirkulárisé ±1; χ értéke lineáris esetben nulla, cirkuláris esetben 45°.
Jones-vektor[szerkesztés]
A polarizációs állapot leírható az összetevő rezgések amplitúdójával és fázisszögük közötti kapcsolattal. Ezt használtuk az előbb, amikor bemutattuk a különböző polarizációs állapotokat. Ezek az információk reprezentálhatók egy két dimenziós komplex vektorral, a Jones-vektorral:
ahol és az amplitúdók, míg és a fázisszögek. A Jones-vektor egységnyi abszolútértékű komplex számmal szorozva egy másik Jones-vektort ad, ami ugyanazt a polarizációs állapotot reprezentálja. A fizikai vektormező ekkor különbözik az eredetitől, mivel a polarizációs állapot független az abszolút fázisszögtől. A Jones-vektor bázisának nem kell valósnak lennie, ami lineáris polarizációt jelentene; használhatók más, ortogonális polarizációs állapotok is. Gyakori választás a jobb és a bal körpolarizáció, ami a cirkulárisan poláros fényre kettős törésű közegekben terjedő hullámok és a cirkuláris polarizáció irányára érzékeny koherens detektorok jelútjainak leírását egyszerűsíti.
Koordináta-rendszer[szerkesztés]
A paraméterezés implicit tartalmazza a koordináta-rendszer irányítását. Ez meghagyja a z tengely körüli forgás szabadságát. A földfelszínnel párhuzamos fénysugarakkal való foglalkozáskor gyakran a vízszintes és a függőleges szavakkal jellemzik a polarizációt, ahol az elsőt a Jones-vektor első komponenséhez, valamint a nulla azimuthoz kapcsolják. Másrészt a csillagászatban az egyenlítői koordináta-rendszert használják, ahol a nulla azimut (más néven pozíciószög a félreértések elkerülésére) az északi iránnyal egyezik.
s és p jelölés[szerkesztés]
Egy másik gyakran használt koordináta-rendszer a beesési síkkal áll kapcsolatban. Ezt a síkot a beeső sugárzás terjedési iránya és valamelyik, a felszínnel párhuzamos lapra merőleges irány határozza meg. Az ezzel a síkkal párhuzamos polarizáció p-szerű, az erre merőleges irányú polarizáció s-szerű. A p és az s rövidítések német eredetűek, a p a parallel, az s a senkrecht szavakra utal. Az ezekben az irányokban polarizált fény p-polarizált, illetve s-polarizált. A p-polarizációra utalnak úgy is, mint transverzális-magnetikus (TM) polarizáció, pi-polarizáció vagy érintősík polarizáció. Az s-polarizáció más elnevezései transverzális-elektromos (TE), szigma-polarizáció vagy nyílirányú polarizáció.
További problémák[szerkesztés]
Mivel a fényforrások polarizálatlan fényt bocsátanak ki, azért szükség van arra, hogy az általánosabb esetet is leírják. További okok az inkoherencia vagy a térbeli inhomogenitások, amik már nem írhatók le Jones-mátrixokkal. Ekkor Stokes-4 vektorokat és 4×4-es mátrixokat (Mueller-mátrixok) használnak. Először Paul Soleillet használta őket 1929-ben. Míg a Jones-mátrixoknak van Mueller-mátrixuk, ez fordítva nem igaz. Ezekkel leírható a szóródás komplex felületeken vagy részecskéken, ahogy azt majd megmutatjuk.[14]
Koherenciamátrix[szerkesztés]
A Jones-vektor a monokromatikus hullámok esetén a polarizáció mellett a fázist is jelzi. Tiszta polarizációs állapotot reprezentál. Ezzel szemben nem tud jellemezni akár különböző polarizációs állapotokat, akár különböző frekvenciákat. Az úgynevezett részlegesen polarizált sugárzás esetén a mezők sztochasztikusak, és az egyes komponensek közötti korreláció és variáció csak statisztikusan írható le. Egy ilyen reprezentáció a koherenciamátrix:[15]
ahol a szögletes zárójelek több teljes cikluson át tartó átlagolást jelölnek. Többféle koherenciamátrixot is használnak: a Wiener-féle és a Richard Barakat-féle koherenciamátrix a jel spektrumának koherenciáját méri. A Wolf-féle koherenciamátrix a teljes időt és spektrumot számításba veszi.
A koherenciamátrix tartalmazza az összes másodrendű információt a polarizációról. A mátrix két idempotens mátrix összegére bontható. Ezek megfelelnek a mátrix sajátértékeinek, amelyek ortogonális polarizációs állapotokat reprezentálnak. Egy másik felbontás egy szinguláris és skálázott identitásmátrix összetevőkre bontja, amelyek rendre a teljesen polarizált és a polarizálatlan összetevőket jelenti. Az utóbbi adja meg a polarizáció fokát. Ez a polarizált összetevő hozzájárulása a teljes intenzitáshoz.
Stokes-paraméterek[szerkesztés]
Nem könnyű szemléltetni a koherenciamátrixot, ezért megszokott, hogy inkább különféle paraméterekkel jellemzik az inkoherens vagy részben polarizált sugárzást. Ezek: a teljes intenzitás I; a polarizáció szöge, p; és a polarizációs ellipszis alakját jellemző paraméterek. Egy matematikailag is kedvező leírás a Stokes-paramétereké, amiket Stokes 1852-ben vezetett be. A kapcsolatot a következő egyenletek adják meg.
Itt Ip, 2ψ és 2χ a polarizáció három dimenziós polarizációs állapotai. A kétszeres szorzótényezőket Stokes azért vezette be, mert a polarizációs ellipszis középpontosan szimmetrikus. A paramétereket néha I, Q, U és V betűkkel jelölik.
Poincaré-gömb[szerkesztés]

A négy paraméter közül az elsőt elhagyva a többi három kirajzolható a Descartes-koordináta-rendszerben. Adott intenzitás mellett az összes polarizációs állapot a
gömböt adja. Ez a Poincaré-gömb. Gyakran nem érdekes a teljes intenzitás, ekkor a Stokes-vektort normalizálják:
ezzel az normalizált Stokes-vektor egységnyi hosszú, és a három normalizált Stokes-paraméter az egységgömbön van. A részlegesen polarizált állapotok a gömb belsejét alkotják. Ha a nem polarizált állapot nem érdekes, akkor egy további normalizáció is végezhető:
A pont az egységgömbön van, és a polarizált komponens állapotát jellemzi.
A Poincaré-gömbön az átellenes pontok az ortogonális állapotoknak felelnek meg. Bármely két polarizációs állapot átfedése csak a gömbön mért távolságuktól függ. Ezek a tulajdonságok egyértelműen jellemzik a Poincaré-gömböt.
Hullámterjedés[szerkesztés]
Vákuumban az elektromágneses mezők állapotváltozása fénysebességgel terjed. Így a síkhullám e vektora a +z irányban:
ahol k a hullámszám. Ahogy korábban megjegyeztük, az elektromos mező megkapható a Jones-vektor és az fázistényező szorzatának valós részeként. Ha a hullám kapcsolatba lép az anyaggal, akkor terjedését az anyag (komplex) törésmutatója befolyásolja. Ha ennek valós vagy komplex része függ a polarizációs állapottól, akkor az anyag kettős törésű, vagy dikroát. A hullám polarizációs állapota megváltozik.
Az ilyen közegekben terjedő elektromágneses hullámok bármely polarizációs állapota felbontható két ortogonális irányú összetevőre, amelyek terjedése különböző. Ekkor a hullám komponenseinek változása könnyen kezelhető egy kétszer kettes Jones-mátrixszal:
A Jones-mátrix függ a terjedési távolságtól és a kettős töréstől. A kettős törésű anyag általában diszperzív, azaz a mátrix függ a frekvenciától is. Ha a közeg nem kettős törésű, akkor a Jones-mátrix identitásmátrix lesz, ami azt jelzi, hogy az anyag nem hat a polarizációs állapotra.
A terjedésre való hatás az
alakú mátrixszal jellemezhető, ahol g1 és g2 komplex számok, amelyek a fáziskésést és az elnyelődést írják le. T egy unitér mátrix, ami leírja a bázisváltást a Jones-vektor bázisába. Lineáris kettős törés és kettős elnyelés esetén az elemek maguk is polarizációs állapotok, úgyhogy megfelelően választott bázis esetén nincs szükség a transzformációra.
Kettős törés[szerkesztés]

Kettős törésű anyagokban a hullámok amplitudója nem változik, a Jones-mátrix unitér: |g1| = |g2| = 1. Az anyag a hullámok fáziskésésére hat. A polarizációtól függő elnyelésű dikroát anyagok Hermitikus mátrixszal írhatók le. Valójában minden mátrix felbontható unitér és pozitív Hermitikus-mátrixok szorzatára, így minden anyag leírható, ami kombinálja a két hatást.
Kettős törésű anyagok ismert példái bizonyos kristályok. A belépő polarizációs fény iránya megváltozik, kivéve ha polarizációja megegyezik valamelyik bázispolarizációval. A polarizációs állapot fáziseltolódás miatti megváltozása rendszerint függ a hullámhossztól, fehér fényben és két keresztezett irányú polarizátor között a szivárvány színeiben tündökölnek.
A cirkuláris kettős törést optikai aktivitásnak is nevezik, különösen a királis folyadékokban, vagy Faraday-rotációnak, ha a terjedés irányába ható mágneses mező hozza létre. Ha lineárisan polarizált fény halad át egy ilyen testen, akkor lineárisan polarizált marad, hanem a polarizáció iránya elfordul. A lineáris és a cirkuláris kettős törés kombinációja két, egymásra ortogonális elliptikus polarizáció; azonban az elliptikus polarizáció elnevezést nem szokták használni.
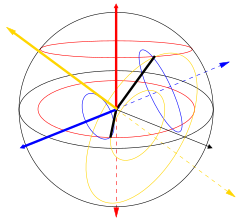
A lineáris kettős törés (merőleges tengelyeket feltételezve) ábrázolható úgy, hogy beérkezik egy ezekhez képest 45° -ban polarizált hullám. Amikor egy differenciális fázis bekövetkezik, akkor a polarizáció 90°-os fáziskülönbségű elliptikus polarizáció lesz, majd a fáziskülönbség eléri a 180°-ot, és ismét lineárissá válik. Ezután a fáziskülönbség tovább nő, 270°-nál újra körpolarizáció lesz, de most a másik irányú, majd a fáziskülönbség teljes körré válik, és a 360° megtétele után az eredeti állapot áll vissza, majd a ciklus kezdődik elölről. Az általánosabb eset bonyolultabb, ahogy az ábra mutatja. A példák mutatják a lineáris (kék), cirkuláris (piros) és elliptikus (sárga) kettős törést. A teljes intenzitás és a polarizáció szöge megmarad. Ha az út hossza megfelelő, akkor a kilépő sugár komponensei helybéli eltolódással lépnek ki, akkor is, ha végső terjedési irányuk ugyanaz lesz. Ezt például kalcitkristályokon lehet látni, amelyeken át nézve az alatta levő tárgyak két példányban látszódnak némi eltolódással. A képek polarizációja egymás ellentéte. Erasmus Bartholinus először ez alapján fedezte fel a polarizációt 1669-ben.
Dikroát tulajdonság[szerkesztés]
Dikroát az a közeg, amiben az elnyelődés függ a polarizáció irányától. Ez érinthet lineárisan (főként kristályok) vagy cirkulárisan (folyadékok) polarizált hullámokat is.
A polarizációs szűrők olyan eszközök, amelyek valamelyik polarizációt teljesen kiszűrik. Ez a Jones-mátrixban megfelel a g2=0 esetnek. A szűrő kimenete egységes polarizációs állapotú, és egy sugár annyit őriz meg intenzitásából, amennyi az áteresztett polarizációs irányba tartozó komponenseinek intenzitása volt. A többi polarizációs irányhoz tartozó intenzitás elnyelődik. Egy ideális polarizációs szűrőn (g1=1 és g2=0) áthaladó polarizálatlan fény az eredeti intenzitásának felét őrzi meg. A gyakorlatban használt polarizációs szűrők azonban az áteresztett irányban polarizált fény egy részét is elnyelik, g1 < 1. Minőségüket az g1 : g2 arány jelzi. Mivel a Jones-vektorok az amplitúdót jellemzik, azért a nem kívánt irányban maradt polarizált fény intenzitása (g2/g1)2.
Törés és tükröződés[szerkesztés]
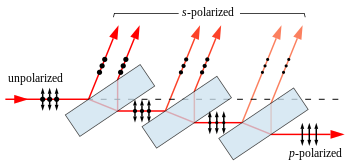
A kettős törés és a dikroát tulajdonságokon kívül a törésmutató polarizációtól való függése is leírható Jones-mátrixszal. A két különböző törésmutató határfelületén történteket a Fresnel-egyenletek írják le. A hullám egy része átjut, másik része visszaverődik; ez függ az anyagtól és a beesési szögtől, és különbözőek az s és a p polarizációkra. Így a visszavert hullám polarizációja megváltozik, még ha eredetileg polarizálatlan volt is.
Van egy szög, amiben ha beesik egy hullám, akkor a p polarizáció visszaverési együtthatója zérus, és a visszavert hullámok s polarizációjúak lesznek. Ez a Brewster-szög. Ezt az elvet használják a polarizátorsorozatokban, ahol az s-polarizáció hullám visszaverődik, így az átmenő hullámok főként p-polarizációjúak lesznek. A p-polarizáció kisebb visszaverődési együtthatója miatt a polarizációs napszemüvegek a káprázást is kivédik.
Fontos az a speciális eset is, amikor az s- és a p-polarizáció együtthatói megegyeznek. Ekkor a kétféle polarizáció ugyanúgy viselkedik, nem szűrődik ki egyik sem. Azonban a cirkulárisan poláros hullámok iránya megfordul, jobbkezesről balkezesre vált, és viszont, mivel a kezességet mindig a terjedés irányához képest állapítják meg. Az x-y tengelyek körül polarizált +z irányba terjedő hullám jobbkezes, míg a -z irányú balkezes. Még általánosabb esetben nem lehet ilyen kijelentéseket tenni, a cirkuláris, elliptikus és lineáris polarizációk átmehetnek egymásba, és megőrizhetik, vagy felcserélhetik kezességüket. Ezek azonban jól leírhatók a Jones-vektorral és a Fresnel-együtthatókkal.
Alkalmazások[szerkesztés]
Mérési módszerek[szerkesztés]
A polarizációt felhasználják különféle mérésekhez. Sok más technika számára is fontos a polarizáció, vagy legalábbis számolni kell vele.
Stressz mérése[szerkesztés]

A mérnöki technikákban a stressz által indukált kettős törés lehetővé teszi az átlátszó anyagokban keletkezett belső feszültségek megjelenítését. A kettős törés függ a színtől is, emiatt a vizsgált tárgyon színes mintázat jelenik meg, ha két polarizátor között nézik. A külső erők hatására keletkező feszültség hatása is látszik a mintázat változásán. A módszert gyakran celofánnal mutatják be, aminek kettős törését a gyártás során elvégzett nyújtás okozza.
Ellipszometria[szerkesztés]
Az ellipszometria egy módszer, ami a földfelszín optikai tulajdonságait elemzi. Ide tartozik a visszaverődő hullámok mérése a szín és a beesési szög függvényében. Mivel a visszaverődésen alapul, a vizsgált mintának nem kell átlátszónak lennie, és nincs szükség a hátoldalhoz való hozzáféréshez sem.
Ellipszometria segítségével mérhető a felszín (komplex, elnyelést is magában foglaló) törésmutatója is mérhető és modellezhető. Hasznos az egy szubsztrátumon fekvő több vékony réteg tulajdonságainak elemzésére is. A visszaverődés tulajdonságait műszerrel mérik, így nemcsak a p és az s polarizációk határozhatók meg, hanem relatív fáziseltolódásuk is. Az ellipszométer általában nem méri közvetlenül a teljes visszaverődést, hanem csak az s és p polarizáció arányát, és az elliptikusság változását. Gyártási folyamatok ellenőrzésére is alkalmas.[16][17]
Földtan[szerkesztés]

Sok kristály (lineárisan) kettős törésű, ami a polarizáció felfedezéséhez is elvezetett. Az ásványtanban mérik is ezt polarizációs mikroszkóppal, ami segít az ásvány azonosításában.
Mivel a szilárd anyagokban terjedő hang nem teljesen longitudinális, hanem vannak transzverzális komponensei is, a hang is polarizálódhat. A polarizált hullámok terjedésének figyelése nélkülözhetetlen a szeizmológia számára. A nyírási hullámok polarizáltak, a vízszintes és a függőleges irányú polarizációk jele SH és SV, míg a longitudinális összenyomási hullámokra P-hullámokként utalnak.[18][19]
Kémia[szerkesztés]
A kémia az ásványtanhoz hasonlóan használja a polarizációt, de az ásványok helyett oldatokat vizsgál. Folyadékokban lineáris kettős törés nem jöhet létre, viszont ha az oldat királis molekulát tartalmaz, akkor cirkuláris kettős törés jön létre. Ha a jobbos (D) és a balos (L vagy S) enantiomerek egyenlő arányban vannak jelen, akkor nincs kettős törés, a folyadék racém. Ha valamelyik túlsúlyban van, akkor az oldat elforgatja a polarizált fény síkját a megfelelő irányba. Ezt polariméterrel mérik.[14][20]
Csillagászat[szerkesztés]
A csillagászatban a polarizáció a világűr tulajdonságait jellemzi. A csillagok által kibocsátott sugárzás polarizálatlan, de polarizált a mézerek és az erős rádióhullámokat kibocsátó objektumok sugárzása az aktív galaxismagokban vagy a pulzárok sugárzása. Emellett a csillagfény is polarizálódik, szóródás vagy a Faraday-forgás által létrejött csillagközi mágneses tér miatt[21][22] kozmikus háttérsugárzás polarizációjából következtetnek a korai Univerzum fizikájára.[23][24] A szinkrotronsugárzás eleve polarizált. Egyes vélemények szerint az űrbéli források okozták a szerves molekulák kiralitás szerinti kiválasztódását.[25]
Általánosabb alkalmazások[szerkesztés]
Polarizációs szemüvegek[szerkesztés]

A polarizálatlan fény visszaverődéssel részben polarizálttá válik. Ezt először Étienne-Louis Malus figyelte meg 1808-ban. A polarizációs szemüvegek éppen ezt használják ki azzal, hogy kiszűrik a vízszintes felületekről visszaverődő polarizált fényt, így kiküszöbölik a káprázást.
A viselők néha zavaró polarizációs jelenségeket figyelnek meg, mint a színtől függő kettős törés, például az autó ablaküvegén vagy átlátszó műanyagból készült tárgyakon. Ennek oka a visszaverődés vagy szóródás miatti polarizáció. Az LCD képernyők polarizált fénye is nagyon feltűnő.
Az ég polarizációja és a fényképezés[szerkesztés]

Az égből érkező fény is polarizált a Föld légkörén történő átkelés közbeni szóródás miatt. Ez a fény adja az égbolt színét és annak élénkségét; emiatt felhasználható arra, hogy az eget kékebbnek mutassa a fényképeken. Ez a legerősebben a Naphoz képest 90 fokban figyelhető meg. A polarizációs szűrők ezt is tekintetbe veszik.[14][26]
Az égbolt polarizációja a tájékozódáshoz is használható. Az 1950-es években az égi iránytűt használták a mágneses sarkok közelében, ahol sem a Nap, sem a csillagok nem voltak láthatók, köd vagy a hosszú szürkület miatt. Egy elmélet szerint a vikingek napkő segítségével figyelték meg a polarizációt, és így tájékozódtak a tengeren a 9-11. században.[1] Ezt azonban egy vizsgálattal cáfolták.[27]
Képalkotás[szerkesztés]
A folyadékkristályos képalkotás (LCD) technológiája azon alapul, hogy a folyadékkristályok tömbje elforgatja a lineárisan polarizált fény polarizációs síkját. A hátsó oldalról érkező fény először egy vékony polarizáló rétegen halad át, majd az aktuális kristályrétegen, ami lehet pixelekbe rendezve, mint a TV vagy a számítógép képernyője, vagy lehet rendezve máshogy, például szimbólumokba. A folyadékkristályos réteget jobb vagy bal kiralitású anyag alkotja, rendszerint apró spirálokból áll. Ez cirkuláris kettős törést hoz létre, amit úgy terveztek, hogy 90 fokkal fordítsa el a lineárisan polarizált fény polarizációját.
Ha egy cellán feszültség halad át, akkor a spirálok kiegyenesednek, amivel megszűnik a cirkuláris kettős törés. A képernyő túloldalán egy másik lineárisan polarizáló réteg található, aminek iránya merőleges az első polarizáló rétegére. Így amikor nincs cirkuláris kettős törés, akkor a cella sötét lesz, mert a fény polarizációja megmarad. Amikor van, akkor a polarizáció síkja elfordul, a fény akadálytalanul halad át mindhárom rétegen, és a cella kigyullad. A két feszültség közötti értékek különböző mértékben forgatják el a polarizáció síkját, így különböző fényességi fokozatok is létrehozhatók. Így működik ma majdnem minden képernyő és kijelző. Ennek az a hátránya, hogy polarizációs szemüveggel ezek a képernyők csak egy bizonyos irányból olvashatók.
A 3D tévé és mozi passzív szemüveges technikája úgy működik, hogy a néző két szemének szánt képanyagot egymásra merőleges polarizációval vetítik, amit a néző olyan szemüveggel néz, aminek lencséi polarizációs szűrősek, de az egyik az egyik, a másik a másik irányban polarizált fényt ereszti át. Így színes filmek is vetíthetők.[28] A képek leadásához használhatnak két vetítőt, de elterjedtebb, hogy egy vetítő van, és a képek között váltogatják a polarizációt. Régebben lineáris polarizációt használtak, de áttértek a cirkuláris polarizációra , hogy a fejmozgások ne zavarják a látványt. A képernyőnek meg kell őriznie a fény polarizációját; erre nem alkalmasak a széles körben elterjedt vászon felületek.
A CRT képernyők szűrőjében kihasználták, hogy a tükröződés általában megfordítja a cirkuláris polarizáció irányát. Ezek a képernyők üvegfelszínük miatt visszatükrözték a külső fényeket, ami zavarta a felhasználókat. A szűrő tükrözte a beeső fényt, és éppen a tükörképükkel blokkolta a zavaró fényeket. Ez a jelenség megfigyelhető, ha 3D mozis szemüvegben nézünk tükörbe, és behunyjuk egyik szemünket. A nyitott szem nem látja a tükörképét, de a csukott szemét igen.
Rádióhullámok[szerkesztés]
A rádióantennák eleve polarizált hullámokat adnak és vesznek, a merőleges polarizációra érzéketlenek. Egyes esetekben a polarizáció az iránytól függ. A legtöbb antenna névlegesen lineárisan polarizált, de előfordulhat elliptikus vagy cirkuláris polarizáció is. Mivel általában az elektromágneses hullámok polarizációjának irányának az elektromos mező polarizációs irányát tekintik, a rádióhullámoknál is ugyanaz a konvenció, mint a fénynél.
A legtöbb antenna lineárisan polarizált. Valójában, ha az adó és a vevő egy síkban van, akkor a polarizációnak ebbe a síkba kell esnie. Ez többnyire teljesül is. Egy tipikus Yagi vagy log-periodikus antenna vízszintes vezetőkkel egy vízszintes irányban levő vevő számára vízszintesen polarizált hullámokat ad. De egy whip antenna vagy egy AM adótorony függőleges polarizációval ad, még ha a vevő vízszintesen is helyezkedik el a toronyhoz képest. Egy négy karú keresztdipól antenna vízszintesen elhelyezve vízszintes polarizációval ad, felfelé irányítva cirkulárisan polarizált lesz az adása. Köztes állapotokban elliptikusan polarizált lesz az adása.
A polarizáció azért fontos a rádiózásban, mert ha nem a megfelelő polarizációval próbáljuk fogni az adást, akkor a jel gyenge lesz, esetleg nem sikerül fogni. A műholdas tévében ezen az elven megduplázzák a sávszélességet. Egy frekvencián két adó sugározhat egymás zavarása nélkül, és a vevő választhatja ki az antenna beállításával, hogy melyiket fogja.
Mivel van földfelszín, azért a rádióhullámok terjedése függ a polarizáltságuktól.
- A hosszú- és középhullámú rádióadók függőleges polarizációt használnak, mivel a felületi rádióhullámok lényegesen jobb hatásfokkal terjednek függőlegesen polarizált formában.
- Rövidhullámoknál az ionoszféráról visszavert rádióhullámok depolarizálódnak, így térhullámok általi összeköttetések során a polarizáció hatása jelentéktelen.
- Ultrarövid-, deciméteres-, és mikrohullámok esetén a felhasználás módja, valamint szabvány határozza meg a polarizációt. Hegyvidéki országokban általában függőleges polarizációt használnak műsorszórásra.
Az alacsony frekvenciákon kerülik a vízszintes polarizációt, mert a talajról visszaverődve a hullám fázisa tükröződik. Ezek interferálnak az eredeti hullámmal, és különösen távol nagyon gyenge lesz a jel. Függőleges polarizáció esetén nincs ilyen probléma.
A radar szempontjából is számításba kell venni a polarizációt és a tükröződést a kibocsátásnál és a vételnél is. Az esőcseppeken való szóródás hatása cirkuláris polarizációval kiküszöbölhető. A hullámhossznál lényegesen kisebb tárgyakon történő visszaverődés interferál az eredeti hullámmal, így egy nagyon gyenge jel keletkezik. Másrészt viszont egy nagy fémtárgy a polarizációt nemcsak tükrözi, hanem meg is változtatja, és ez jel.
Az ionoszférában levő szabad elektronok a Föld mágneses terével kölcsönhatásba lépve Faraday-rotációt idéznek elő, ami a cirkuláris kettős törés egyik fajtája. Ez ugyanaz a mechanizmus, ahogy a csillagközi térben az elektronok elforgatják a lineáris polarizációt. Mértéke alacsony frekvenciákon nagyobb, nem zavarja azokat a magasabb mikrohullámú frekvenciákat, amiket a műholdak használnak. Ellenben a közepes és a rövidhullámú közvetítéseket már igen. Mivel egy hullám útja megjósolhatatlan, így végeredményben a polarizáció bármilyen irányú lehet.
Szögmomentum cirkuláris polarizáció esetén[szerkesztés]
Jól ismert, hogy az elektromágneses sugárzás bizonyos lineáris centrális momentumot hordoznak terjedésük irányában. A cirkulárisan (vagy elliptikusan) polarizált hullámoknak emellett szögmomentumuk is van. Az alacsonyabb frekvenciákkal, például a mikrohullámokkal szemben a fény szögmomentuma elhanyagolható lineáris momentumával szemben, még mérése is nehézségekbe ütközik. Kísérleti körülmények között azonban sikerült felhasználni akár 600 milliós percenkénti fordulatszám elérésére.[29][30]
Jegyzetek[szerkesztés]
- ↑ a b c d J. David Pye. Polarised Light in Science and Nature. CRC Press (2001. február 13.). ISBN 978-0-7503-0673-7
- ↑ Sonja Kleinlogel (2008. április 12.). „The secret world of shrimps: polarisation vision at its best”. PLoS ONE 3 (5), e2190. o. DOI:10.1371/journal.pone.0002190. PMID 18478095.
- ↑ "No evidence for polarization sensitivity in the pigeon electroretinogram", J. J. Vos Hzn, M. A. J. M. Coemans & J. F. W. Nuboer, The Journal of Experimental Biology, 1995.
- ↑ Karl Fent: Polarized skylight orientation in the desert ant Cataglyphis. Journal of Comparative Physiology A, 158 (2), 1986, S. 145–150, doi:10.1007/BF01338557.
- ↑ Rüdiger Wehner: Polarization vision – a uniform sensory capacity? The Journal of Experimental Biology 204, 2001, S. 2589–2596, PMID 11511675.
- ↑ Griffiths, David J.. Introduction to Electrodynamics, 3rd, Prentice Hall (1998. április 12.). ISBN 0-13-805326-X
- ↑ Geoffrey New. Introduction to Nonlinear Optics. Cambridge University Press (2011. április 7.). ISBN 978-1-139-50076-0
- ↑ Dorn, R. (2003. december 1.). „Sharper Focus for a Radially Polarized Light Beam”. Physical Review Letters 91 (23), 233901. o. DOI:10.1103/PhysRevLett.91.233901.
- ↑ a b M. A. Sletten and D. J. McLaughlin, "Radar polarimetry", in K. Chang (ed.), Encyclopedia of RF and Microwave Engineering, John Wiley & Sons, 2005, ISBN 978-0-471-27053-9, 5832 pp.
- ↑ Merrill Ivan Skolnik (1990) Radar Handbook, Fig. 6.52, sec. 6.60.
- ↑ Hamish Meikle (2001) Modern Radar Systems, eq. 5.83.
- ↑ T. Koryu Ishii (Editor), 1995, Handbook of Microwave Technology. Volume 2, Applications, p. 177.
- ↑ John Volakis (ed) 2007 Antenna Engineering Handbook, Fourth Edition, sec. 26.1. Megjegyzés: Más szerzőkkel szemben reciprokként definiálja az elliptikusságot, mint a kis- és a nagytengely arányát, de amikor decibelekben kezdi el kifejezni, a kényelem kedvéért elhagyja a negatív előjelet, így azt kapja, mint a többi szerző.
- ↑ a b c Hecht, Eugene. Optics, 4th, United States of America: Addison Wesley (2002. április 12.). ISBN 0-8053-8566-5
- ↑ Edward L. O'Neill. Introduction to Statistical Optics. Courier Dover Publications (2004. január 1.). ISBN 978-0-486-43578-7
- ↑ Polarized Light, Revised and Expanded. CRC Press (2011. január 3.). ISBN 978-0-203-91158-7
- ↑ Masud Mansuripur. Classical Optics and Its Applications. Cambridge University Press (2009. április 12.). ISBN 978-0521881692
- ↑ Peter M. Shearer. Introduction to Seismology. Cambridge University Press (2009. április 12.). ISBN 978-0-521-88210-1
- ↑ An Introduction to Seismology, Earthquakes, and Earth Structure. John Wiley & Sons (2009. április 1.). ISBN 978-1-4443-1131-0
- ↑ Organic Chemistry, Fourth Edition: Structure and Function. W. H. Freeman (2003. április 12.). ISBN 978-0-7167-4374-3
- ↑ Vlemmings, W. H. T. (2007. március 1.). „A review of maser polarization and magnetic fields”. Proceedings of the International Astronomical Union 3 (S242), 37–46. o. DOI:10.1017/s1743921307012549.
- ↑ Fundamental Astronomy. Springer (2007. június 27.). ISBN 978-3-540-34143-7
- ↑ Boyle, Latham A. (2006. április 12.). „Inflationary predictions for scalar and tensor fluctuations reconsidered”. Physical Review Letters 96 (11), 111301. o. DOI:10.1103/PhysRevLett.96.111301. PMID 16605810.
- ↑ Tegmark, Max (2005. április 12.). „What does inflation really predict?”. JCAP 0504 (4), 001. o. DOI:10.1088/1475-7516/2005/04/001.
- ↑ Clark, S. (1999. április 12.). „Polarised starlight and the handedness of Life”. American Scientist 97 (4), 336–43. o. DOI:10.1511/1999.4.336.
- ↑ Electromagnetic Vibrations, Waves, and Radiation. USA: MIT Press (1977. április 12.). ISBN 0-262-52047-8
- ↑ Élet és Tudomány, 2016
- ↑ http://www.geeks.hu/technologiak/100127_minden_amit_a_3d_rol_tudni_erdemes
- ↑ "University of St Andrews scientists create 'fastest man-made spinning object'"
- ↑ "Laser-induced rotation and cooling of a trapped microgyroscope in vacuum", Research @ St. Andrews
Fordítás[szerkesztés]
- Ez a szócikk részben vagy egészben a Polarization című angol Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.
- Ez a szócikk részben vagy egészben a Polarization című német Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.