Erős kölcsönhatás
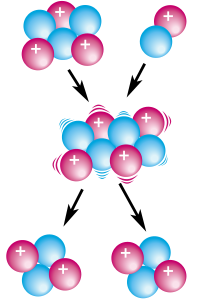
Az erős kölcsönhatás egyike a természet négy alapvető kölcsönhatásának, a legerősebb közülük. Közvetítőrészecskéi a gluonok. A kvarkok, antikvarkok és maguk a gluonok között is hat.
Megfigyelni viszont csak a hadronok közötti kölcsönhatást lehet, és mint magerőket, mivel szabad kvarkokat és gluonokat eddig nem sikerült megfigyelni. A magerők olyan maradék kölcsönhatások a protonok és neutronok között az erős kölcsönhatás esetén, mint a van der Waals-erők az atomok és molekulák között az elektromágneses kölcsönhatás esetén.
Története[szerkesztés]
Ernest Rutherford 1911-es kísérletében kimutatta egy kis méretű, nagy tömegű atommag létezését az atomok belsejében. Eleinte úgy gondolták, hogy a mag protonokból és elektronokból áll – ezzel azonban nem lehetett megmagyarázni az atommagok nagy stabilitását –, mígnem James Chadwick 1932-ben a neutron felfedezésével be nem bizonyította, hogy töltött protonokból és semleges neutronokból. A magban tehát csak pozitív töltések voltak, fel kellett hát tételezni egy új erős kölcsönhatást a nukleonok – protonok és neutronok – között, ami képes legyőzni a protonok elektromos taszítását.
Ekkoriban a protonokat, neutronokat, majd a később felfedezett egyre több hadront még valódi elemi részecskének, azaz alapvető részecskéknek gondolták, ezért a köztük ható erőket gondolták az elsődleges erős kölcsönhatásnak, s nem csak maradék kölcsönhatásnak. Jukava Hideki megpróbált egy potenciált találni az erőtér leírására, ahogy az 1/r-es potenciál kitűnően leírja az elektrosztatikus erőket. Eredménye egy bizonyos fokig közelítésként működik, de máig sem sikerült megtalálni az erős kölcsönhatást jól leíró potenciált.
A mag leírására különféle empirikus magmodellek születtek, mint George Gamow cseppmodellje, amik többé-kevésbé jól közelítették a magok tulajdonságait és a nukleáris technikában használható jóslatokat adtak.
Az 1950-es években a hadronok osztályozása során Gell-Mann és Nishijima összefüggést ismert fel a hadronok töltése, izospinje és ritkasága között, végül 1961-ben Gell-Mann és Neemán oktettekbe ("Nyolcas út") és dekuplettekbe csoportosította a már ismert hadronokat, néhánynak a létezését a hiányzó helyeken meg is jósolva. 1964-ben azután Gell-Mann és George Zweig felállították a kvarkmodellt, ami a sok ismert hadront három hipotetikus részecskéből kvarkból rakta össze.
Az erős kölcsönhatást nagy energiájú szórások esetén az 1965-ben a Moo-Young Han, Nambu Joicsiro és Oscar W. Greenberg által javasolt új belső kvantumszám a szín SU(3)-terén alapuló kvantumtérelméletnek a kvantum-színdinamikának sikerült leírnia. Az elmélet 1973-ra vált általánosan elfogadottá.
Kvantum-színdinamika[szerkesztés]

A kvantum-színdinamika (QCD) egy kvantumtérelmélet, a lokális belső (szín)-SU(3) szimmetrián alapuló mértékelmélet. Az elektromágneses kölcsönhatás kvantumtérelméletének, a kvantumelektrodinamikának a sikere inspirálta, hogy a többi kölcsönhatást is megpróbáljuk mértéktérelméletként leírni. A QCD csatolási állandója alacsony energián nagy, ezért ott nem alkalmazható a perturbációszámítás, és alacsony energián, azaz a kötött állapotok (hadronok, atommagok) energiáján nem sikerült az egyenletek megoldása. Itt továbbra is empirikus modellekre, valamint rács-QCD-számolásokra kell hagyatkoznunk. Nagyobb energián (ütközések, szórások) esetén viszont a csatolási állandó csökken és ott működik a perturbációszámítás, a kísérleti eredményekkel megegyező jóslatokat szolgáltatva.
Gluonok[szerkesztés]
A gluonok az erős kölcsönhatás közvetítő bozonjaiként az elektromágneses kölcsönhatás fotonjának megfelelői. Mivel azonban az SU(3)-csoport az elektromágneses U(1)-gyel ellentétben nem kommutatív (nemabeli), ezért a gluonoknak van önkölcsönhatások, azaz a gluonoknak is van színük, nem csak a kvarkoknak. A gluonoknál ezt a színt mintegy "kettős színként" képzelhetjük a hétköznapi analógia nyelvén beszélve, azaz például "piros-antikék", ami a kimenő "piros" és bejövő "kék" kvarkok közötti átmenetet biztosítja. Maga a kölcsönhatási pont – mint a Lagrange-függvény egy eleme – azonban összességében színtelen.
A csatolási állandó[szerkesztés]
A csatolási állandó a Lagrange-függvény kölcsönhatási tagjának együtthatója, ami kísérletileg meghatározandó külső paraméterként van az elméletbe betéve. Az elméletben meghatározható az energiafüggése (impulzusátadás-függése), így már csak egy pontban kell kísérletileg meghatározni.
Az impulzusátadás növekedésével, azaz a kölcsönhatási távolság csökkenésével a csatolási állandó csökken, amit aszimptotikus szabadságnak hívunk. Ez általában jellemző a nemabeli (nem kommutatív) mértékelméletekre, ezért:
- Nagy impulzusátadás esetén lehetséges a perturbációszámítás, amikor a csatolási állandó már elég kicsi, vagyis kisebb egynél, s ezért a korrekciók egyre kisebbek, az eredmények konvergálnak.
- Kötött állapotok belsejében, ahol az alkotórészek nagyon közel vannak egymáshoz, lényegében szabadon, szinte kölcsönhatásmentesen léteznek egymás mellett, ám amikor el akarnak távolodni egymástól egy bizonyos távolságon túl, akkor a felerősödő kölcsönhatás megakadályozza őket ebben. Ez nyilván fontos szerepet játszik a kvarkbezárásban, azaz, hogy nem tudunk az elsődleges erős kölcsönhatásban részt vevő részecskéket (kvarkokat és gluonokat) egyedül megfigyelni. Ezen a kvalitatív képen alapulnak általában a kötött állapotok modelljei, mint például a zsákmodell.
Kötött állapotok[szerkesztés]
A QCD egyenleteit sajnos nem tudjuk analitikusan megoldani, és a túl nagy méretek esetén – az atommag és a hadronok mérete már ilyen – a túl kicsi impulzusátadás miatt a futó csatolási állandó túl nagy (nagyobb egynél) ahhoz, hogy perturbációszámítással lehessen számolni.
Az egyik kiutat az egzakt egyenletekből kiinduló rács-QCD számolások jelentik, ami bonyolult algoritmusok és szuperszámítógépek használatát igényli a rendkívüli forrásigényű számításokhoz. Egyébként közelítő modelleket kell használni.
Jukava-modell[szerkesztés]
Közvetlenül az erős kölcsönhatás felfedezése után, amikor a nukleonokat még elemi részecskéknek hitték, Jukava Hideki alkotta meg az erős kölcsönhatás első modelljét, ami az ún. Jukava-potenciállal – vagy más néven árnyékolt Coulomb-potenciállal – próbálta leírni a nukleonok között ható erőket:
Ez a potenciál megfelel egy m tömeggel rendelkező mezon cseréjével létrejövő kölcsönhatásnak, ami m=0 esetén átmegy a Coulomb-potenciálba. Eleinte úgy gondolták, a π-mezonok ezek a tömeges közvetítő részecskék. A modell végül nem bizonyult helyesnek, de viszonylag alacsony energiákon jó közelítő számolásokat tesz lehetővé.
Hadronmodellek[szerkesztés]
A legtöbb hadronmodell valamilyen erős határfeltétellel igyekszik bezárni a kvarkokat a hadronok belsejébe, például hogy a határon eltűnik, vagy érintőleges az áramuk iránya. Vagy valamilyen speciális topológiai választással érik el ugyanezt a kényszert. Ilyen modellek például
- MIT zsákmodell
- skyrmion modell vagy sündisznó-modell – Tony Skyrme elméleti fizikus nevéből
- királis zsákmodell – az MIT zsákmodell és a skyrmion modell kombinációja
Magmodellek[szerkesztés]
A magmodellek külön csoportot alkotnak, mivel a nukleonok között ható erők az erős kölcsönhatás másodlagos erői (nukleáris van der Waals-erők), azaz más a viselkedésük, mint a hadronokon belül a kvarkok között ható elsődleges erőknek.
- George Gamow cseppmodellje, ami egy folyadékcsepp belső szabadságával és felületi feszültségével modellezi a magot
Az erős kölcsönhatás tulajdonságai[szerkesztés]
Kvarkbezárás[szerkesztés]

Az erős kölcsönhatás egyik fontos jellemzője, hogy nem figyelhetünk meg szabad kvarkokat, amit kvarkbezárásnak nevezünk. A jelenségre egzakt magyarázat nincs, de szinte bizonyítottnak tekinthető.
Az egyik népszerű szemléltetés a következő. Két kvark közötti erőtér alakja nem hasonlít a Coulomb-térre (vagy a hozzá hasonló mágneses térre), ahol a tér önkölcsönhatása híján az erővonalak betöltik az egész teret, s ezért az erőközponttól nagyobb távolságra a kisebb erővonalsűrűség miatt kisebb a hatóerő, ill. magában az erőközpontban a sokfelé húzó erők miatt az eredő viszonylag kicsi. Az erős kölcsönhatás erővonalai a tér önkölcsönhatása miatt egymáshoz közel húzódnak, a tér csőszerűen összehúzódik, mint egy kábelköteg. Ezért az erővonalköteg mentén állandó az erő és az energiasűrűség (ami viszonylag nagy). Szabad kvark a végtelenre való eltávolításnak felelne meg, ehhez viszont végtelen energiát kellene közölni vele a mindig állandó erő miatt. Ugyanakkor viszonylag nagy a valószínűsége a nagy energiasűrűség miatt, hogy az erővonalköteg mentén egy kvark-antikvark pár keletkezzen, az erővonalköteg egy szakaszának energiája árán. Az erővonalköteg így felszakad és egyik új vége az egyik, másik új vége a másik keletkezett új (anti)kvarkban ér véget, azaz az eredeti egy mezon helyett két új mezonunk van már, de továbbra sem figyelhetünk meg kvarkot szabadon.
Ha a kvarkok energiáját növeljük, akkor egy darabig távolodnak, ha túllépjük azt az energiát, amely egy kvark-antikvark pár keletkezéséhez elegendő, akkor egy kvark-antikvark pár keletkezik, de ismét kötött állapotban maradnak az alábbi két ábrának megfelelően (az eredeti kvarkokat (*) távolítjuk, újak (+) keletkeznek, de kötött (-) állapotban):
- *-*
- *-+ +-*
További információk[szerkesztés]
- Trócsányi Zoltán: Kvarkok csodálatos világa, 2010. július 25. (Hozzáférés: 2011. december 22.)

