Csillagászati színképelemzés
A színképelemzés vagy spektrumanalízis az összetevőire bontott elektromágneses sugárzás, a színkép vizsgálatát jelenti. A színképelemzéssel foglalkozó tudományágat spektroszkópiának nevezzük.
A csillagok atmoszférájának az összetételére és a fizikai állapotára vonatkozó ismereteinket a csillagászati színképelemzés eredményei tették lehetővé. (Az általános értelemben vett színképelemzéshez lásd: Spektroszkópia.) A csillagászati színképelemzés során megvizsgálják az egyes hullámhossztartományok intenzitását, erősségét ill. fényességét, továbbá az ún. Fraunhofer-féle vonalak helyzetét és szélességét. Ez utóbbiakat a földi anyagok színképelemzési eredményeivel összehasonlítva bizonyos elemeknek és vegyületeknek a csillag légkörében való előfordulására következtethetünk. A fényintenzitás folytonos színképi eloszlása a hőmérséklettől és az anyagi összetételtől függ, így ebből meghatározható a csillagok egyik legfontosabb tulajdonsága, a felszíni hőmérséklet. A színképvonalak Doppler-eltolódásának vizsgálatával információt nyerhetünk a csillag látóirányú (radiális) sebességéről, majd ebből közvetve – kettős vagy többesrendszer esetén – a rendszer tagjainak tömegére és egyéb fizikai tulajdonságaira következtethetünk.
A csillagászati színképelemzés története[szerkesztés]
| Fraunhofer- jelölés |
Hullámhossz (nm) |
A vonal kémiai eredete |
Ekvivalens szélesség (pm) |
|---|---|---|---|
A spectrum kifejezést Newton használta először annak a jelenségnek a megfigyelése kapcsán, hogy a napfény egy prizmán áthaladva színekre bomlik. Bár erről a felfedezésről egy kézírásos dokumentum szerint a Royal Societynek 1672-ben számolt be először, egy korábban megírt leveléből a fehér fény színekre bontásának felfedezését 1666-ra tehetjük. A Nap fényében láthatatlanul jelenlévő színekre használta a latin eredetű spectrum szót.[1] Felfedezéséről és észrevételeiről később az 1704-ben megjelent Optika című művében is írt, ahol tisztázta a színek természetét.
A 18. század elején többen (Descartes, Hooke, Herschel) is kísérleteztek a Nap fényének felbontásával. A jelenség behatóbb tanulmányozása Wollaston (1766–1828) nevéhez fűződik, aki rést is alkalmazott a kísérleteinél, és elsőként fedezte fel a napszínkép abszorpciós (elnyelési) vonalait. Szám szerint 7 spektrumvonalat figyelt meg – köztük a Na-kettős vonalát (dublett) –, jelentőségüket azonban nem ismerte fel. Ez egy német fizikus, Joseph von Fraunhofer (1787–1826) nevéhez köthető. Fraunhofer építette meg az első spektroszkópnak nevezett eszközt, ebben a diszperzív optikai elemként használt prizmán és a résen kívül kollimátorlencse is volt a fény útjában, ez gyűjtötte össze a fénysugarakat. Ezzel a berendezéssel Fraunhofer a Nap spektrumában mintegy 600 vonalat (mai néven Fraunhofer-féle vonalak) talált; melyek közül 350-nek a pontos pozícióját is meghatározta, kiszámítva az általuk kitakart színek hullámhosszát. Ezzel 1814-ben megszületett a csillagászati spektroszkópia.
Fraunhofer felfedezésével egy időben, 1823-ban, W. H. Fox Talbot és John Herschel (William Herschel fia) különféle elemekkel festett lángok színképét vizsgálták, és utaltak rá, hogy ez alapján kémiai analízis végezhető. Brewster 1832-ben felfedezte, hogy a Fraunhofer-féle vonalak földi fényforrással is előállíthatók. A salétromsav gőzén átbocsátott napfény színképében mintegy 2000 vonalat számlált meg. Azt is megfigyelte, hogy a vonalak száma nő, ha növeljük a gázréteg vastagságát, sűrűségét vagy hőmérsékletét. E kísérletei nyomán Brewster úgy gondolta, hogy a Nap fehér fényéből a Föld légköre szűr ki bizonyos színeket, és ezek helyén észleljük a Fraunhofer-féle vonalakat. 1849-ben Foucault különféle eredetű színképek vizsgálatával szintén egy alapvető felismerésre jutott: a spektrum abszorpciós vagy emissziós volta attól függ, hogy a fény közvetlenül a fényforrásból érkezik-e hozzánk, vagy a fényforrást elhagyva egy adott anyagon haladt át. 1859-ben Foucault, és Bunsen (1811–1899) eredményeit felhasználva Kirchhoff (1824–1887) felállította a klasszikus spektrumanalízis három alaptörvényét:


- Az izzásig hevített szilárd testek, folyadékok, valamint a magas hőmérsékletű és nagynyomású gázok folytonos spektrumú elektromágneses sugárzást bocsátanak ki, mindenféle színképvonalak nélkül. Ez a kontinuum.
- Világító gázok kisebb nyomás és alacsonyabb hőmérséklet mellett különálló, fényes emissziós vonalakat mutatnak. Minden egyes kémiai elemhez egyedi vonalsorozat tartozik; valamely világító gáz emissziós színképe tehát elárulja a gáz kémiai összetételét.
- Ha egy önmagában folytonos színképet adó anyag fénye egy hűvösebb gázon halad keresztül, akkor a kontinuumon azoknál a hullámhosszaknál jelentkeznek sötét abszorpciós vonalak, amelyeknél az átvilágított gáz emissziós vonalakat adna, ha önmaga világítana. Tehát minden kémiai elem a rá jellemző hullámhosszokon nyel el és bocsát ki sugárzást.

A színképelemzések eredményei alapján Kirchhoff és Bunsen 1860–61-ben két új kémiai elemet fedezett fel: a céziumot és a rubídiumot.
Azt, hogy az egyes csillagok színképei különböznek egymástól, már Fraunhofer megállapította. A csillagokat színképeik alapján először Angelo Secchi (1818–1878) sorolta osztályokba — először csak három osztályt különített el; majd az átmenetek miatt a rendszert két továbbival bővítette.
A következő lépés az Edward Charles Pickering vezette Harvard-obszervatóriumban főleg Antonia Maury és Annie Jump Cannon mérései alapján kidolgozott rendszer, amelynek csoportjait az ábécé nagybetűivel jelölték. 1900 táján az addigi munkát kritikusan átvizsgálták, egyes csoportokat megszüntettek, a korábbi sorrendet megváltoztatták, így alakult ki a ma használatos csillagászati színképosztályozás alapja, a Harvard-osztályozás, amelyben az osztályok O–B–A–F–G–K–M sorban a fehértől a vörös felé haladva, tehát a hőmérséklet csökkenésének rendjében követik egymást (ezt a sort később egészítették ki az R, N és S különleges osztályokkal). Ezt a rendszert használva adták ki 1903-ban első fotografikus atlaszukat az északi félgömb 12 magnitudónál fényesebb csillagairól.[2]
A csillagászati színképelemzés elméleti alapjai[szerkesztés]
A színképvonalak és színképsávok kvantumos elmélete[szerkesztés]
A színképelemzés kvantumos elméletét csak sokkal később, a Bohr-féle atommodell (1913) megszületésekor dolgozták ki. Eszerint folytonos sugárzás keletkezik olyan szabad elektronoknak a lehetséges energiaszintek (pályák) valamelyikére történő ugrásnál, amelyek előtte az atommagok között szabadon mozogtak. Az egyedi esetekben keletkező sugárzás hullámhossza az elektron befogása előtti állapot energiájának és az elért pálya energiaszintjének különbségével arányos (Bohr III. törvénye alapján). Mivel az eredetileg szabad elektronok energiája jelentősen eltér egymástól, ezért a befogási folyamatnál jelentősen eltérő hullámhosszak keletkeznek, amelyek egyetlen kontinuummá „kenődnek szét”.
Tehát a színképeknél alapvetően két típust különböztetünk meg: folytonos és nem folytonos színképek. A nem folytonos színképek lehetnek vonalasak vagy sávosak, ami attól függ, hogy a színképet létrehozó részecske atom-e vagy molekula. A vonalas színképeket szériesz- és multiplett-spektrumokra osztjuk. Szériesz-spektrumoknál az alapnívóhoz magasabb nívók végtelen sorozata csatlakozik. Ilyen színképe van az egy vegyértékelektronnal rendelkező atomoknak, például a hidrogénnek. Az elektron lehetséges energiaállapotainak feltüntetésére a termeket használjuk. Multiplett spektrumok a több vegyértékelektronnal rendelkező atomok esetében jönnek létre, ekkor a termséma bonyolultabbá válik, aminek megfelelően bonyolultabbak és sokrétűbbek lesznek a spektrumok is; vonal helyett vonalcsoportok, azaz multiplettek jönnek létre. A molekulák energiaátmeneteiből kapott színképek sávosak, mivel egy-egy energiaszint sok, egymástól nem sokban különböző alszintre bomlik, emiatt a vonalak egymáshoz szorosan közel helyezkednek el. Így a molekulák vonalas színképének tanulmányozásához nagy felbontású spektroszkópiai eszközökre és különleges technikára van szükség. A molekulák színképvonalai jóval bonyolultabb módon alakulnak ki, mint atomok színképvonalai. Itt ugyanis az elektronok mozgásán kívül az atommagok rezgéseket végeznek a magokat összekötő molekulatengely mentén, bizonyos egyensúlyi magtávolság környezetében, továbbá az egész molekula forog a súlypontján átmenő, a molekulatengelyre merőleges tengely körül. Ezért közelítőleg – a háromfajta mozgás közti kölcsönhatás elhanyagolásával – a molekula teljes energiája az elektron-, a rezgési és a forgási energia összege. A molekula rezgése és forgása különböző meghatározott energiaszinteken lehetséges. Amikor egy magasabb energiaszinten lévő gerjesztett molekula alacsonyabb szintre megy át, az energiakülönbséget egy foton formájában sugározza ki. Mindezek alapján a sávos molekulaszínképeknél három típust különböztetünk meg:
- tiszta rotációs (forgási) színkép keletkezése során csak a forgási energia változik meg, az elektronállapot és a rezgésállapot nem. Ezek a molekulasávok a távoli infravörösbe és a mikrohullámú tartományba esnek.
- vibrációs-rotációs spektrumok kvantumátmenetei esetében megváltozik a rezgési állapot és a rotációs állapot, változatlan az elektronállapot. Ezek a sávok a közeli infravörös (NIR) tartományba esnek.
- elektronsáv-színképek esetében mindhárom állapot megváltozik. Az így keletkezett sávok az ultraibolya (UV), a látható (VIS), vagy az infravörös (IR) tartományba esnek.
Az elektronsáv-színképek vizsgálata azért lényeges, mert segítségével meghatározható a magtávolság, a magrezgések frekvenciája illetve az elektronok elrendeződése. Az egyes elektronállapotokat bizonyos kvantumszámokkal és szimmetria tulajdonságokkal lehet jellemezni. Így például az atomok s, p, d, f,.. állapotaihoz hasonlóan megkülönböztetünk Σ, Π, Δ, Φ,… molekulaállapotokat aszerint, hogy az elektronok teljes impulzusmomentumának vetülete a molekulatengely irányára h/2π-nek 0, 1, 2,…-szerese.
A csillagászati színképelemzéseknél megfigyelt molekulák mind egyszerű felépítésűek, legtöbbjük kétatomos, ami a csillagok légkörének magas hőmérsékletével magyarázható. Magas hőmérsékleten ugyanis a molekulák disszociálnak (szabad atomokra bomlanak fel). A molekulasávok ezért a viszonylag hidegebb csillagok (például barna törpék) spektrumában figyelhetők meg.
Csillagászati színképelemzésnél bizonyos esetekben előfordulhatnak a spektrumban ún. tiltott vonalak. Ezek olyan színképvonalak, amelyek laboratóriumi körülmények között nem jöhetnek létre, mivel keletkezésükhöz extrém fizikai körülmények (például rendkívül kis sűrűség) szükségesek. Tiltott színképvonalak például az egyszeresen és kétszeresen ionizált oxigén (O+, O2+), a háromszorosan és négyszeresen ionizált neon (Ne3+, Ne4+), az egyszeresen és kétszeresen ionizált kén (S+, S2+), a háromszorosan és négyszeresen ionizált argon (Ar3+, Ar4+) vonalai. Legfontosabb az atomos hidrogén 21 cm-es rádióvonala, amely az alapállapotú elektron két ellentett spinű beállása közti kicsiny energiakülönbségnek felel meg. Az ilyen vonalak létrejöttéhez szükséges feltételek teljesülnek az emissziós ködökben. Ezek az objektumok általában 10–100 parszek átmérőjűek, sűrűségük pedig rendkívül alacsony, legfeljebb 10 ezer atom/cm³.
A hidrogénatom és a hidrogénszerű ionok spektruma[szerkesztés]
A Fraunhofer-féle vonalak keletkezésének folyamatát akkor lehet megérteni, ha a fény abszorpcióját és emisszióját a legegyszerűbb atom, a hidrogénatom modelljén magyarázzuk meg. Ha a hidrogénatom elektronja megváltoztatja állapotát, és egy másik, kisebb főkvantumszámú állapotot vesz fel, akkor az energiakülönbséget fénykvantumként kisugározza. A fény frekvenciája , a hullámszáma (az egy cm-re jutó hullámhossz) . . A hidrogénatom színképében a következő sorozatok találhatók:

| Lyman-sorozat | |||
| Balmer-sorozat | |||
| Pascen-sorozat | |||
| Brackett-sorozat | |||
| Pfund-sorozat |
A Lyman-sorozat az ultraibolya, a Balmer-sorozat a látható, míg a többi sorozat az elektromágneses sugárzás infravörös tartományában helyezkedik el. A hidrogén egyszerű színképével szemben a nehezebb atomok (növekvő tömegszám szerint) spektrumai egyre bonyolultabbá válnak. A hidrogénszerű ionok, vagyis az egyszeresen ionizált hélium (He+), a kétszeresen ionizált lítium (Li2+), a háromszorosan ionizált berillium (Be3+) stb. spektrumai erős hasonlóságot mutatnak a hidrogénatom spektrumával, mert ezeket a rendszereket szintén egy elektron alkotja, ahol csak a magtöltés és tömegszám emelkedik. A Bohr-féle atommodell szerint az ilyen ionok lehetséges energiaértékei a H-atom energiaértékeinek Z²-szeresei:
Az ionizált hélium (He+-ion, Z=2) által kibocsátott sorozatok egyike a Dzéta Puppis csillag színképében még 1897-ben felfedezett Pickering-sorozat:
amelyet kezdetben a hidrogénatom színképvonalainak tekintettek. A Bohr-elmélet nyomán azonban a fenti sorozatot megtalálták a He+ színképében, héliumban létesített kisülések alapján.
Az alkáliatomok színképe[szerkesztés]

Az alkáliatomok a periódusos rendszer I. főcsoportjában helyezkednek el, azaz legkülső elektronhéjukat egy elektron alkotja, ezért az elemek közül a hidrogénhez hasonlítanak a legjobban, amelyben összesen csak egy elektron van. A legkülső elektron világító elektronnak vagy vegyértékelektronnak nevezzük. Az előbbi elnevezés arra utal, hogy az alkálifémek optikai színképe ennek az elektron a gerjesztése során jön létre, utóbbi elnevezés pedig az atom kémiai viselkedésében betöltött szerepét fejezi ki. A vegyértékelektron atomtörzsön belüli tartózkodási valószínűsége a mellékkvantumszámtól függ, ezért energiája – ellentétben a hidrogénatommal – a főkvantumszám mellett a mellékkvantumszámtól is függ.
| Az s állapot energiája | ahol | |
| A p állapot energiája | ahol |
c a fénysebesség, h =6,626·10−34 Js (Planck-állandó), R =1,097·107 m−1 (Rydberg-állandó), s ill. p korrekciós tagok (hidrogénatom esetén értékük 0) annál nagyobbak, minél nehezebb az atom, és minél kisebb az l mellékkvantumszám értéke. (A hidrogénatomhoz hasonlóan az l mellékkvantumszámnak kisebbnek kell lennie a főkvantumszámnál.) Az optikai színkép úgy jön létre, hogy két energiaszint közötti különbség fénykvantum formájában kisugárzódik. Az emissziós színkép vizsgálatakor négy intenzívebb, részben egymásba nyúló vonalsorozat figyelhető meg: a fősorozat, az első és második melléksorozat, valamint a Bergmann-sorozat:
| Fősorozat | ahol | |||
| II. melléksorozat | ahol | |||
| I. melléksorozat | ahol | |||
| Bergmann-sorozat | ahol |
Abszorpcióban rendszerint – ha az alkáligőz nem nagyon magas hőmérsékletű – csak a fősorozat jön létre. Mindegyik sorozat határához folytonos színkép – határkontinuum – csatlakozik, hasonlóan a hidrogén színképeinek esetéhez.
Az alkáliföldfémek színképe[szerkesztés]

Az alkáliföldfémek a periódusos rendszer II. főcsoportjában helyezkednek el, vegyértékhéjukat emiatt két elektron alkotja. A magnézium színképében szinglettek (különálló vonalak) és triplettek (vonalhármasok) sorozatai fordulnak elő, amelyek fel vannak tüntetve a Grotrian-diagramon. Kombinációkat nem figyeltek meg a szinglettek és triplettek között, de ez a kiválasztási szabály gyakran sérül ahogy az összetett atomok irányába haladunk a periódusos rendszer II. főcsoportjában. A magnéziumnál az 1's állapotból az alacsonyabb energiájú 3³p állapot közepébe történő átmenetnek van jelentősége a csillagászatban.
Általánosságban az atomok energiaszintjeinek multiplicitását a vegyértékelektronok száma határozza meg. Az egy vegyértékelektronnal rendelkező magnéziumnál dublettek (vonalkettősök), a kettő vegyértékű magnéziumnál szinglettek és triplettek, a három vegyértékű alumínium színképében dublettek és kvartettek (vonalnégyesek) fordulnak elő. Az ionizált atomok energiaszintjeinek multiplicitása megfelel a vele azonos vegyértékhéjjal rendelkező atoméval.
A színképvonalak multiplicitása[szerkesztés]
A sugárzás elnyelése és kibocsátása[szerkesztés]
A Bohr-féle atommodell energiaszintjei stacionárius állapotok; az egyik állapotból a másikba történő átmenet csak valamilyen másik részecskével történő kölcsönhatás útján lehetséges (a fénykvantumot itt részecskéknek tekintjük). A kölcsönható részecske által kiváltott folyamat alapvetően kétféle lehet: gerjesztés vagy ionizáció. Gerjesztés során az atom egy olyan gyors elektronnal lép kölcsönhatásba, amely elegendő energiával rendelkezik ahhoz, hogy az atomot alapállapotból gerjesztett állapotba juttassa. Ezt általánosan így jelöljük:
- A + egyors → A* + elassú (1) A* → A + hν (2) A + hν → A* (3)
ahol A* a gerjesztett atomot, e pedig az elektront jelöli. A gerjesztett atom arra törekszik, hogy minél hamarabb alacsonyabb energiájú állapotba jusson, amit (2) folyamattal érhet el. Itt a hν szorzat egy fénykvantumot jelöl. Minden folyamat, amely egy atom gerjesztéséhez vezet, megfordítható (reverzibilis). Ekkor fénnyel történő gerjesztésről (3) beszélünk.
Ionizáció során az atom nagyenergiájú elektronokkal (4) vagy fotonokkal (5) ütközik, melynek hatására az atom elektronja olyan mértékben gerjesztődik, hogy elhagyja az atomot. A reakciót a következőképpen jelölhetjük:
- A + egyors → A+ + e + elassú (4) A + hv → A+ e + Ekin (5)
ahol A+ egy olyan atomot jelöl, amelyből hiányzik egy elektron, és ezért +e töltésű. A megfordított folyamatot, amelynek során egy elektron befogása történik, miközben egy másik elektron a szabaddá vált energiát felveszi, hármas ütközés általi rekombinációnak nevezzük. A befogott elektron ilyenkor közvetlenül az alapállapotba juthat, vagy először egy gerjesztett állapotba, ahonnan kisugározva a rá jellemző vonalas színképnek megfelelő frekvenciájú fotont, eléri az alapállapotot. Annak az elektronnak a szerepét, amelyet nem fognak be, és a befogott elektron energiáját felvette, más atomok és molekulák is átvehetik. Az ionizáció végbemehet fotonok befogásával is, ekkor fotoionizációról beszélünk. A fotoionizáció feltétele, hogy a foton energiájának nagyobbnak kell lennie, mint az elektron alapállapotának és a sorozathatárnak a különbsége. Ez a reakció azt jelenti, hogy egy atom nem csak a rá jellemző színképnek megfelelő fotonokat képes elnyelni a (3) egyenletnek megfelelően, hanem a sorozathatárnál nagyobb energiájúakat is, és közben pozitív ionok keletkeznek, ami egyezik a tapasztalattal. A fotoionizáció fordított folyamatát sugárzással járó rekombinációnak nevezzük. Ennek során az ion egy elektront fog be, és ezáltal semleges atommá alakul. Ez többféleképpen is végbemehet:
- A+ + e + Ekin → A + hv (6) A+ + e + Ekin → A* + hv1 → A + hv1 + hv2 (7)
Színképvonalak keletkeznek az ún. perturbáció jelenség során is. Ilyenkor egy szabad elektron egy atom közelében repül el, gyorsulást szenved, és – mint gyorsuló töltött részecske – elektromágneses sugárzást bocsát ki. Mivel az elektron szabad állapotai nem kvantáltak, ilyenkor folytonos emisszió lép fel.
Vonalprofilok, vonalkiszélesedés, ekvivalens szélesség[szerkesztés]

A színképvonalak nem végtelenül keskenyek, a sugárzás intenzitása a kontínuumtól a vonal közepe felé mindkét irányból folyamatosan csökken vagy nő, aszerint, hogy a vonal abszorpciós vagy emissziós. Ha az intenzitást a hullámhossz függvényében ábrázoljuk, akkor a vonalprofilt (vonalkontúrt) kapjuk. A középső szakaszt vonalmagnak, a két külső részt vonalszárnynak nevezzük, a három rész együtt a vonal szélességét adja. A gyakorlatban a szomszédos vonalak gyakran összeolvadnak („blend”), és ilyenkor nehéz mérni a vonal szélességét. A vonal erősségét az ekvivalens szélességgel jellemezzük. Ha a színképvonal intenzitását ahhoz az intenzitásegységhez viszonyítva ábrázoljuk, amely a kontínuumban a vonal helyén beérkezne, akkor a vonalprofil által körülfogott terület a vonal teljes abszorpciója. Az ezzel egyenlő területű, egységnyi magasságú téglalap szélessége a vonal szélessége. Ångströmben mérjük, definíciója:
Ahol Fc a kontinuum fluxusa, Fλ pedig a színképvonalon belüli fluxus, vonalprofil. (Az egyes színképvonalak ekvivalens szélességének fizikai paraméterektől való függésére a Schuster–Schwarzhild-féle modellből következtethetünk.) A színképvonalprofil azért jön létre, mert a színképvonal frekvenciatartományában a abszorpciós koefficiens megnövekszik, mivel ebben a frekvenciaintervallumban képes valamelyik atom abszorbeálni az elektromágneses spektrumot. Ahhoz, hogy a vonalprofil alakját elméleti úton meg tudjuk határozni, ismernünk kell a függését a frekvenciától. Az abszorpciós koefficiens két részből tevődik össze: folytonos abszorpciós koefficiensből és szelektív abszorpciós koefficiensből. A színképvonalon kívül csak -vel számolunk, a színképvonal frekvenciatartományában a összeggel.
Az rν = Iν / Iνo mennyiséget maradékintenzitásnak nevezzük. Ahol ν a folytonos színkép frekvenciája, Iνo az ehhez tartozó intenzitás, Iν a valódi intenzitás a színképvonal frekvenciatartományán belül. A színképvonal frekvenciatartományán kívül rν = 1; a színképvonalon belül rν < 1

A csillagok fotoszférájában keletkező színképvonalak profilját a folytonos és a szelektív abszorpció együttesen alakítja. A szelektív abszorpciónak két fajtája van. Bizonyos esetekben csak az egyik vagy csak a másik fajta abszorpció játszik szerepet (például a napkorong szélén csak a tiszta szórás). Valódi szelektív abszorpció során a foton abszorbeálódik valamilyen atomban és gerjeszti azt. A gerjesztett elektron 10·10−12 s alatt alacsonyabb állapotba kerül, de valódi ~ esetén nem a kiindulási állapotba, vagyis az elnyelt foton energiája nem egyezik meg az emittált foton energiájával. Tiszta szórás esetén a ν1 frekvenciájú foton abszorpciója után az emittált foton ismét ν1 frekvenciájú lesz. Mivel az emisszió izotropnak tekinthető, ezért tiszta szórás esetében egy párhuzamos sugárnyalábból izotrop sugárzás jön létre.
Egy adott csillag (fényforrás) vonalprofiljainak vizsgálata azért lényeges, mert belőlük az égitest több fizikai tulajdonságára következtethetünk:
- A csillagok légkörét alkotó gáz fizikai körülményei
- Forgási sebesség
- Esetleges pulzáció
- Csillagszél
- Tömegvesztés
- Felszíni foltok (csillagfoltok)
- A csillagot körülvevő anyag
- kettőscsillag lehetősége
A spektrumvonalak kiszélesedése
A vizsgálatok alapján kiderült, hogy a spektrumvonalak nem végtelen keskeny vonalból állnak, hanem van bizonyos kiterjedésük, amely a hullámhossztól függ. A jelenség a természetes vonalkiszélesedés, amit a Heisenberg-féle határozatlansági relációval magyarázhatunk. A reláció szerint az egymással fel nem cserélhető fizikai mennyiségek értékét nem tudjuk meghatározni egyidejűleg és egyforma pontossággal. Például egy kvantumállapot energiájára és élettartamára a következő összefüggés áll fenn: ahol τ a gerjesztett állapot élettartama, h a Planck-állandó, δE pedig a kvantumállapot energiabizonytalanságát jelöli. A vonalkiszélesedés másik oka az ún. ütközési csillapodás, vagy nyomási vonalkiszélesedés. Ennek az az oka, hogy az atomok ütközéseinek hatására lerövidül egy-egy gerjesztett állapot időtartama, így hamarabb visszatérnek az alapállapotba. A vonalkiszélesedés harmadik oka a termikus kiszélesedés (Doppler-kiszélesedés), amely általában 1-2 nagyságrenddel nagyobb mértékű, mint a természetes vonalkiszélesedés. Ezeken a mikrofizikai folyamatokon kívül további vonalkiszélesedést okozhat még a csillagok rotációja és/vagy pulzációja is.
A Doppler-eltolódás okozta vonalkiszélesedés mérését közvetlenül befolyásolja a spektrográf felbontása (nm/pixel; ångström/pixel). Ha ugyanis sebességegységekben mérünk, akkor a Doppler-formula a következőképpen írható fel: ahol Δλ az észlelt hullámhossztartomány centrálisa, λ a spektrográf felbontásának mértéke, c a fénysebesség és v a radiális sebesség.
Hőmérsékleti sugárzás[szerkesztés]

A csillagok többségénél a spektrumvonalak bizonyos (néha elég széles) tartományaiban az energia viszonylagos eloszlása közel áll az abszolút fekete test színképében tapasztalható energia eloszláshoz, amelyet a Planck-féle képlet ad meg, ez hullámhosszal kifejezve:
ahol h a Planck-állandó (h=6,62·10−34 J s) k a Boltzmann-állandó (k=1,38·10−23 J/K) c a fénysebesség, T pedig a test abszolút hőmérséklete. A Planck-törvény – csillagászatban is gyakran alkalmazott – két folyománya a Stefan–Boltzmann-törvény és a Wien-féle eltolódási törvény. A Wien-féle eltolódási törvény értelmében a Planck-görbe maximumának megfelelő hullámhossz és a T hőmérséklet szorzata állandó.
A Stefan–Boltzmann-törvény a Planck-törvényből minden frekvenciára és irányra való integrálás útján adódik, és kimondja, hogy a T abszolút hőmérsékletű fekete test egységnyi felületéről egységnyi idő alatt kisugárzott teljes energia a hőmérséklet negyedik hatványával arányos:
- ahol σ = 5,67·10−8 W/m²K4 a Stefan–Boltzmann konstans.
Rövid hullámhosszakon a Planck-függvény helyett a Wien-közelítés alkalmazható:
Hosszú hullámhosszakon viszont a Rayleigh–Jeans közelítés alkalmazható:
A színképvonalak Fowler–Milne-féle elmélete[szerkesztés]
Az atomok elektronhéjában az elektronok csak jól meghatározott (stacionárius) energiaszinteket foglalhatnak el. Az r-szeresen ionizált atom k-dik energiaszintje: (r, k), az ehhez a szinthez tartozó energia Er,k. Az atom csak olyan frekvenciájú sugárzást képes (ionizáció nélkül) abszorbeálni, amelyre vonatkozóan érvényes a következő egyenlőség: h · v = Er,k– Er,l ahol teljesül, hogy k > L.
Az (r, l) → (r, k) átmenethez tartozó színképvonal „erőssége” és profilja attól függ, hogy az adott típusú atomból mennyi található a csillag fotoszférájának egységnyi térfogatában, és hogy a fotoszférában előfordul-e jelentős mennyiségben az r-szeresen ionizált állapot. Azonos körülmények között a színképvonal erőssége függ a csillag atmoszférájában lévő ionizációs viszonyoktól, vagyis a hőmérséklettől.
A Fowler–Milne-féle elmélet a Saha-egyenlet segítségével azt vizsgálja, hogy miként függ egy meghatározott (r, k) szinten tartózkodó elektronok száma, és ezzel hozzávetőlegesen a színképvonal erőssége a hőmérséklettől. A termodinamikai egyensúly esetén érvényes Saha-egyenlet megadja a különböző ionizációs állapotú atomok relatív számát:
ahol nk,r az r -szeresen ionizált k-adik gerjesztett állapotban lévő atomok számsűrűsége, gk,r az egyes állapotok sztatikus súlya (táblázatból nyerhető), ne az elektronsűrűség Xr az ionizációs energia, me az elektron tömege. A csillagok színképében a különböző ionizációs állapotú atomok színképvonalának tanulmányozásából, például a növekedési görbe segítségével meghatározható az arány, amivel az egyenletből kifejezhető a csillag TI ionizációs hőmérséklete. Szintén termodinamikai egyensúly fennállásakor teljesül a Boltzmann-formula, amiből megállapítható a csillag ún. TG gerjesztési hőmérséklete:
ahol nr,k az adott kémiai elem r-szeresen ionizált atomjai közül azoknak a térfogategységre eső száma, amelyek a k-adik kvantumállapotban vannak, Er,k ugyanilyen fajtájú r-szeresen ionizált k-állapotú atom gerjesztési energiája. A csillag színképében azoknak a színképvonalaknak az ekvivalens szélessége amelyeknél az elektronátmenet az r, k állapotból kiindulva történik, arányos nr,k-val. Ugyanazon atom két különböző színképvonal-sorozatának vizsgálatából megállapítható az arány.
Zeeman-effektus[szerkesztés]

Pieter Zeeman (1865–1943) holland fizikus 1896-ban felfedezte, hogy a színképvonalak mágneses mezőben 3 komponensre hasadnak fel. A színképvonalak ún. pí-komponense a helyén marad, a két ró-komponens pedig szimmetrikusan eltolódik a rövidebb illetve a hosszabb hullámhosszak felé. A jelenség magyarázata, hogy mágneses mezőben az atomok mágneses momentuma a megegyező irányban rendeződik. Összesen 2J+1 beállási lehetőségük van, vagyis az atomok energiaállapotai 2J+1 szintre hasadnak fel. Bohr III. törvénye alapján a spektrumvonalak megfelelnek két energiaátmenet közötti energiakülönbségnek. Az energiaállapotok felhasadása a spektrumvonalak felhasadásában figyelhető meg.
Megkülönböztetünk normális és anomális Zeeman-effektust. Normális Zeeman-effektus esetén a fotont emittáló atomoknak csak pálya-impulzusmomentuma van (S=0, L≠0). A felhasadt spektrumvonalak egymás közti energiakülönbsége: ΔW = μB B ahol B a mágneses momentum abszolút értéke. A spektrumvonalak közötti frekvenciakülönbség ekkor:
Δν = ΔW / h ≈ 14 GHz/T . Például a hidrogénatom színképvonalai 1 tesla mágneses indukciójú mezőben ∆v = 1,4·1010 Hz frekvenciakülönbséggel hasadnak fel. Ez a színképben nagyon kis eltéréseket jelent (a nátrium-dublett komponensei közti távolság 3%-át). Kimutatásához a spektrométernek ≥ 106 felbontóképességgel kell rendelkeznie.
Anomális Zeeman-effektus esetén a spektrumvonalat mutató atomban teljesül, hogy L≠0 és S≠0. Emiatt több spektrumvonal jelenik meg, mint normális Zeeman-effektus esetében. A Zeeman-effektus a spektrumvonal komponensek fényének polarizáltságával is jár. Ennek módja és mértéke a mágneses mező és a látósugár által bezárt szögtől függ. A felhasadást egyszerűbb vizsgálni emissziós színképvonalaknál. Ha egy fénykibocsátó gázt mágneses mezőbe helyezünk, és a mágneses mező iránya egybeesik a megfigyelés irányával, akkor normális Zeeman-effektus esetén csak a kettő, eltolódott ró-komponenst figyelhetjük meg, amelyek fénye arra merőlegesen lineárisan polarizált. Általános esetben, ha a mágneses mező iránya a látósugárral γ szöget zár be, a komponensek fényességének arányát az Frederick H. Seares által megfogalmazott formulával adhatjuk meg.
A napfoltok spektrumvonalainak több komponensre való felhasadására G. E. Hale adott magyarázatot, polarizációs mérésekkel igazolta, hogy a felhasadás a napfolt mágneses mezőjében bekövetkező Zeeman-effektus következménye.
A Zeeman-féle jelenség felhasználásán alapul a magnetográf működése. Ez egy olyan berendezés, amelynek segítségével mérhető a Napon kialakuló mágneses mezők erőssége, és meghatározható e mezők területi kiterjedése.
Johannes Stark (1874–1957) német fizikus megfigyelte, hogy erős elektromos mezőbe helyezett gázok színképvonalai is felhasadnak, hasonlóan a Zeeman-effektushoz. A felhasadás a térerősség négyzetével arányos. Ezt a jelenséget Stark-effektusnak nevezzük.
Az égitestek színképe[szerkesztés]
Nap[szerkesztés]
| Kémiai elem | Vegyjel | Tömeg % | Atomszám % |
|---|---|---|---|
| hidrogén | 56% | 84,3% | |
| hélium | 41% | 15,3% | |
| szén | 0,1% | 0,02% | |
| nitrogén | 0,4% | 0,8% | |
| oxigén | 0,8% | 0,08% | |
| neon | 1,2% | 0,1% | |
| vas | 0,2% | 0,01% |
A Nap effektív felületi hőmérséklete a Stephan–Boltzmann-féle sugárzási törvény alapján 5785 °K = 5512 °C. Ezt a hőmérsékletet a Planck-féle sugárzási törvény (1900) és a Wien-féle eltolódási törvényből is le lehet vezetni. A Nap sugárzási maximuma ezek alapján 468 nm-nél van, ami az elektromágneses sugárzás látható tartományába esik.
A Nap színképe folytonos spektrum, amelyre abszorpciós, ritkábban emissziós vonalak rakódnak. A folytonos színkép a fotoszférában keletkezik, az abszorpciós vonalak pedig a fotoszféra fölött elhelyezkedő kromoszférában. (Ma mintegy 25 ezer ilyen abszorpciós vonalat ismerünk, melynek mintegy 75%-át sikerült már azonosítani.) Az emissziós vonalak főként a naplégkör legkülső tartományában, a napkoronában jönnek létre. Ezen vonalak döntő többsége az optikai tartománynál kisebb hullámhosszú tartományba esik. Időszakos emissziós vonalak keletkeznek a napkitörések alkalmával, ekkor jelentős hőmérséklet-növekedés tapasztalható. Ez kb. 1-2 órás jelenség, utána a színképvonalak abszorpcióssá alakulnak.
A színképi vonalak intenzitásából megállapítható a Nap légkörének kémiai összetétele. Az adatok alapján világos, hogy tömegszázalék szerint 97%-ban, atomszám szerint 99,6%-ban a Nap hidrogénből és héliumból, vagyis a két legkönnyebb elemből áll. Az atomokra visszavezethető vonalakon kívül a Nap színképében található néhány színképi sáv is, ezek molekulák jelenlétére utalnak. A magas hőmérsékletnek megfelelően azonban főként olyan vegyületek jöhetnek szóba, amelyek két atomból állnak: OH, NH, CH, SiH, MgH, CaH, C2, CN, O2, TiO, MgO, AlO. A Nap spektrumában a földi légkör is otthagyja a nyomát. Bolygónk légköre hideg gázként viselkedik, elnyeli a Nap fényéből a rá jellemző hullámhossztartományokat.
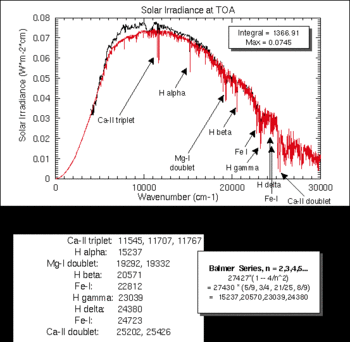
Ezt igazolják a H2O, O2, O3, CO2, N2O, CH4, N2 atomok ill. molekulák napszínképre rakódó elnyelési vonalai, ami zavarja a valódi színkép vizsgálatát. A valódi ill. a Föld légköre okozta spektrumvonalak szétválasztása a naplégkörben keletkező spektrumvonalaktól a Doppler-effektus alapján történik. A földi légkör elemeinek vonalai ugyanis nem szenvednek eltolódást, így könnyen megkülönböztethetőek.
A Napról szerzett ismereteink jelentős részét a színképelemzés elvén működő műszereknek (spektroszkóp, spektrográf, spektrohelioszkóp, spektroheliográf) köszönhetjük. A spektroszkóp a színkép leképzésére szolgál, a spektrográffal pedig a színképet akár le is fényképezhetjük. A Napról azonban egyik sem ad képet. Ha az a célunk, hogy a Napkorongot lássuk, vagy egy felszíni jelenséget vizsgáljunk, de nem a teljes színképtartományban, hanem egy kiválasztott sávban, akkor alkalmazunk spektrohelioszkópot vagy spektroheliográfot. (Utóbbival fényképezni is lehet.) Ezek a műszerek a beépített, ráccsal ellátott ernyő révén csak a kívánt színképsávot engedik át a teljes spektrumból. Ez a spektrális tartomány általában a látható vörös fényt jelenti, mivel ez a tartomány árul el a legtöbbet a Napon végbemenő folyamatokról. A Nap ugyanis nagyrészt hidrogénből áll, a hidrogén által okozott legfényesebb színképvonal a hidrogén-alfa. Ez a vonal a λ = 6,562 81·10−6 m hullámhossznál található. Hidrogén-alfa fényben figyelhetőek meg a napfoltok mágneses tulajdonságai. Két szomszédos napfolt esetén sötétebb „szálak” figyelhetőek meg H-alfa fényben, amelyek nagy ívekben futnak az egyik foltról a másik folt közepe felé, kirajzolva a mágneses erőtér vonalait.
Exobolygók[szerkesztés]
A Naprendszeren kívüli bolygók (ún. exobolygók) kimutatására napjainkban csak közvetett módszerek állnak rendelkezésünkre. A kimutatás történhet a bolygó csillagra gyakorolt gravitációs hatása alapján, mégpedig a csillag mozgásának közvetett (spektroszkópiai) megfigyelésével. A bolygó túl halvány a csillag fényéhez képest és túl közel kering hozzá, hogy távcsövekkel megfigyelhető legyen, de gravitációja közvetve nyomot hagy a csillag színképében. A bolygó és a csillag közös tömegközéppontjuk körüli keringése során a csillag radiális sebessége változik: a Doppler-effektusnak megfelelően a színképvonalak hullámhossza eltolódik, közeledéskor a kék, távolodás esetén a vörös hullámhosszak felé. Spektrográfiai eszközökkel ezt a hullámhosszváltozást mérni lehet, akár 1 m/s-os pontossággal. A Nap tömegközéppontjának mozgásában a Jupiter mintegy 12 m/s, a Föld 0,1 m/s sebességingadozást okoz.
Üstökösök, meteorok, kisbolygók[szerkesztés]
A fényes üstökösök színképe molekulák jelenlétéről árulkodik. A Nap UV-sugarai fluorszcenciát idéznek elő. A kóma és a csóva színképe részben folytonos, ami a Nap visszavert fényére utal, részben fényes vonalakból álló emissziós színkép. Elsősorban a C, H, N és O vonalai ismerhetők fel benne. A kóma semleges és ionizált, a csóva túlnyomórészt ionizált molekulákból áll. A kóma színképében található molekulák a CN, CH, OH, NH, C2, CH2, NH3, ionizált molekulák a CO+, CO2+, OH+, CH+. A csóvában pedig a CN, CO+, CO2+, CH+ és az N2+ sávok fordulnak elő. Az üstökösök színképének első elemzése Swings csillagász nevéhez fűződik.
A meteorok színképben elsősorban a Na, Fe, Ca, Mn, Cr, Si, Ni, Al semleges vonalai és a Ca, Fe, Mg és Si ionizált vonalai figyelhetőek meg. Gyors meteorok ( v > 30 km / s ) esetében a Ca II, H és K vonalak dominálnak. Az ionizációs energiából meghatározható a meteor sebessége az atmoszférába való érkezéskor.
A kisbolygók (aszteroidák) színképe a felszínt alkotó anyagoktól és a felszín állapotától függ. Ez alapján csoportosíthatóak:
- A típus: extrém vörös színű aszteroidák erős abszorpciós vonalakkal, amelyek olivin jelenlétére utalnak. Előfordulásuk ritka.
- B típus: tulajdonságaikban a C típusra hasonlítanak, albedójuk viszont nagyobb. Ritka.
- C típus: igen sötétek, geometriai albedójuk 0,065 alatti. Felszínükön kondrit és hidrált szilikátok vannak jelen. Előfordulásuk gyakorisága 75%. Főleg a Naptól távol gyakori.
- E típus: nagy albedójúak, ensztatit akondritok olvadásos-üvegesedéses folyamatokkal. A Naphoz közelebb gyakoribb.
- F típus: gyenge abszorpciós (elnyelési) vonalakat mutatnak UV-tartományban
- G típus: hasonlít a C-típusra, UV-tartományban erős abszorpciós vonalakat tartalmaz a spektruma
- M típus: spektrumuk alapján fémekből (vas, nikkel stb.) vannak. Valószínűleg nagy, ősi aszteroidák ütközéssel feltárt magjai.
- S típus: a legheterogénebb osztály, a Naphoz relatíve közel (kb. a Föld távolságában) jellemzők. Albedójuk 0,07–0,23 közé esik. Gyakoriságuk 15%. Különböző szilikátok alkotják, felszínükön gyakran figyelhetünk meg sok port, vagy olvadásos-üvegesedéses folyamatok nyomát, amit a fiatal Nap erős sugárzása okozott. Hét alosztályukba ezek alapján lehet tovább osztályozni őket.
- T típus:
- V típus: bazalt anyagú égitestek, jól meghatározott (a 4 Vesta kisbolygóhoz hasonló) pályán keringenek, és valószínűleg a Vesta töredékei.
Csillagok[szerkesztés]
A csillagok légkörét – fizikai tulajdonságai alapján – három részre oszthatjuk. A fotoszféra az atmoszféra legalsó rétege. A nagy nyomás és magas hőmérséklet mellett itt nagyon sok szabad elektron van. Ilyen körülmények között sor kerülhet a legkülönbözőbb pályákra való befogásukra, ami által folytonos színkép jön létre. Természetesen itt nemcsak a hidrogénről van szó, hanem nehezebb, bonyolultabb felépítésű atomokról is. A fotoszféra fölött helyezkedik el az alacsonyabb hőmérsékletű kromoszféra. Ez a réteg hideg gázként viselkedik, éppen azokat az energiamennyiségeket nyeli el, amelyek az elektronok gerjesztett állapotának eléréséhez szükségesek. Ekkor abszorpciós (elnyelési) vonalak keletkeznek. A kromoszféra fölött található a korona, melynek vastagsága nagyobb, mint 106 km. A hőmérséklet itt hirtelen óriásira nő, akár a 106 kelvines nagyságrendet is elérheti. Ilyen fizikai körülmények mellett emissziós vonalak keletkeznek.
Hasonló kémiai összetételük miatt a normális elemgyakoriságú csillagok színképét – a légkörükben jelenlévő gerjeszthető atomokat és ionokat – elsősorban nem a kémiai összetétel, hanem a hőmérséklet és a légkörük nyomása határozza meg. (Ezért egyes elemek vonalainak hiányából nem szabad arra következtetni, hogy ezek az adott csillag légköréből hiányoznak. Ezek az elemek is előfordulhatnak, csak spektroszkópiai úton nem észlelhetőek, mert spektrumvonalaik a Föld felszínén vizsgálható színképtartományokban számottevő mértékben nem fordulnak elő.) A nyomástényező hatása főként a vonalak szélességét befolyásolja: kis nyomás mellett a keletkező vonal keskeny, éles, nagy nyomás esetén szélesebb. Az eltérő vonalintenzitást mutató csillagokat növekvő felszíni hőmérsékletük szerint rendezzük, ezen alapul a Harvard-féle színképosztályozási rendszer. Ez elméletben a csillagokra jellemző legfontosabb színképvonalak erősségének és ekvivalens szélességének megállapításával történik. Ezek a vonalak/vonalsorozatok/sávok az alábbiak:
- a hidrogén Balmer-sorozata
- az ionizált hélium és az ionizált vas vonalai
- a kálium abszorpciós vonala (393.3 nm)
- az ún. G-sáv (CH molekula)
- a semleges kalcium 422,7 nm-es vonala
- 431 nm körüli fémvonalak
- A TiO molekula sávjai
E szisztéma fő hiányossága, hogy nem árul el semmit a csillag luminozitásáról. Többek között a csillagok e fontos paraméterének megállapítására vezették be a Yerkes-féle spektrálklasszifikációs rendszert.

A csillagok színképosztályának megállapítása a gyakorlatban a következőképpen történik. Egy nagy látószögű Schmidt-távcső fényútjába néhány fokos prizmát helyeznek, így a fotolemezen megjelenik minden csillagnak a színképe. Az így kapott spektrumok felbontása azonban nagyon gyenge, részletes tanulmányozásra nem alkalmas, viszont megfelel a spektrálklasszifikáció törvényeinek. Minden színképosztályhoz és alosztályhoz tartoznak standardcsillagok, melyeknek spektráltípusa adott. ( A standardcsillagok listája a csillagászati színképosztályozás szócikkben található. ) Ismeretlen spektráltípusú csillagok esetében a színképosztályokba történő besorolásnál az adott műszerrel először a standardcsillagról kell objektívprizmás felvételt készíteni, majd a kapott spektrumot a csillagéval összehasonlítani.
A spektroszkópiai kettőscsillagok kutatásában különösen fontos szerepe van a csillagászati színképelemzésnek. Ezek olyan kettőscsillagok, amelyekről csak spektroszkópiai úton állapítható meg a kettősség. Mivel a kettős rendszer két csillagkomponense a közös tömegközéppont (baricentrum) körül kering, ezért eközben radiális sebességváltozásokat mutatnak, kivéve ha a keringés pályasíkja merőleges a látóirányra. Ha egy ilyen kettős komponenseinek nagyjából megegyezik a fényessége, akkor két egymásra rakódott színképet látunk, amelyben a színképvonalak egymással ellentétes irányba elmozdulnak. A közeledő komponens vonalai a rövidebb, a távolodó komponens vonalai pedig a hosszabb hullámhossz irányába tolódnak el a Doppler-effektus alapján. Fél periódusidő elteltével fordított a helyzet, amikor pedig a csillagok látóirányra merőleges mozgást végeznek, akkor természetesen nincs Doppler-eltolódás. Összefoglalva a spektroszkópiai kettősök vonalai egy teljes keringési periódus alatt kétszer szétválnak, és kétszer összeolvadnak. Egy ilyen periódust megfigyelve megállapítható a keringési időn kívül a két csillag ellipszispályájának excentricitása (értéke többnyire 0,1 alatti) és a komponensek tömegének aránya.
Csillagközi anyag[szerkesztés]
| Szín | Hullámhossz (nm) | Atom vagy ion | Megjegyzések |
|---|---|---|---|
| ibolya | |||
| ibolya | |||
| ibolya | |||
| kékeszöld | |||
| zöld | |||
| zöld | |||
| vörös | |||
| vörös | |||
| vörös |
A csillagközi anyag kutatása és a csillagok keletkezése mind a mai napig a modern asztrofizika egyik leghomályosabb területe. Az ezzel kapcsolatos legelső számítások Pierre-Simon de Laplace nevéhez fűződnek, akinek elgondolásai mindmáig tükröződnek a modern elméletekben. Ő vetette fel először, hogy a csillagok – bolygóikkal együtt – a csillagközi anyagból, gravitációs összehúzódással keletkeznek. A csillagközi anyag felfedezésére ezután még több mint egy évszázadot kellett várni, hiszen ez a ritka anyag az optikai tartományban nehezen figyelhető meg. Ezért nem meglepő, hogy az első közvetlen megfigyelést csak viszonylag későn, 1904-ben végezték. J. F. Hartmann ekkor a Delta Orionis spektroszkópiai kettős színképét vizsgálva olyan abszorpciós vonalakat (pl.: Ca) talált a spektrumban, amelyek nem vettek részt a spektroszkópiai kettős keringése során bekövetkező egyéb vonalainak periodikus eltolódásaiban, hanem egy állandóan meghatározott hullámhosszon maradtak. Ez úgy magyarázható, hogy a vonalak nem a csillagokból származnak (ekkor ugyanis a Doppler-effektusnak megfelelően vonaleltolódásokat kellene megfigyelni), hanem a csillag és a megfigyelő közötti anyagból.
A csillagközi anyag spektruma folytonos színkép, amire emissziós vonalak rakódnak. E két összetevő intenzitásának aránya a köd típusától függ; a reflexiós ködöknél a folytonos (kékes) színkép, a H II felhőknél, planetáris ködöknél, szupernóva-maradványoknál, intersztelláris buborékoknál pedig az emissziós színkép dominál.
A csillagközi anyagban azonosított atomok és molekulák: Kétatomosak: OH, NH, CH, CO, CS, SiO, SiH, MgH, CaH, C2, CN, O2, TiO, MgO, AlO. Többatomosak: H2O, HCN, HCHO. Találtak már cianoacetilént (HC3N) is, ami 5 atomból álló molekula. Az ilyen molekulák előfordulása az élet kialakulásáról folyó viták (asztrobiológia) szempontjából nem lényegtelen. A vegyületekben leggazdagabb terület a Sagittarius (Nyilas) és az Orion (Kaszás) csillagképben található. Az összetettebb, 6–7 atomot is tartalmazó molekulák több változatát ebben a két csillagképben találták meg. Néhány érdekesebb szerves vegyület ezek közül: formaldehid HCHO, metil-cianid CH3CN, formaldimin CH2NH, metil-acetilén CH3C2H, acetaldehid CH3HCO, formamid NH2HCO és dimetil-éter (CH3)2O.
A galaxisok színképe[szerkesztés]
A galaxisok spektruma az őket alkotó fényesebb csillagok színképének a keveréke. A kontínuumon egyaránt megfigyelhetőek abszorpciós és emissziós vonalak. A spirális galaxisokban a HII tartományok és ionizált hidrogénfelhők vonalai mutatkoznak. Magjuk többnyire M és K típusú csillagokból épül fel, színképükben ezért a kétszeresen ionizált oxigénion vonalai találhatóak meg. A központi tartomány emellett igen széles emissziós vonalakat mutat, ami a csillagközi gáz nagy sebességére (~1000 km/s) utal. A spirálkarokban az I-es populáció fiatal kék forró csillagai figyelhetőek meg. A fénylő csillagközi gázfelhőkkel együtt ezek teszik megfigyelhetővé a spirális szerkezetet. A csillagközi gáz és por néhány száz parszek vastagságú korong formájában a fősíkba tömörül. A színkép összességében az A – F-ig terjedő színképosztályoknak felel meg.
Az elliptikus galaxisok magja – hasonlóan a spirális galaxisokéhoz – is II-es populációba tartozó csillagokból áll. Főként fényes vörös óriások figyelhetők meg, amelyek együttesen a K, L, M színképosztályt képviselik. A csillagösszetételnek megfelelően az elliptikus galaxisok inkább vörösek, a spirálisok pedig kékesek.
A világegyetem tágulása a galaxisok egymástól való távolodásában mutatkozik meg, ezért a galaxisok színképvonalai vöröseltolódást mutatnak. A vöröseltolódás legkönnyebben a kalcium H- és K-vonalánál figyelhető meg, ami a látható ibolya tartományból a kék-zöld tartomány felé történik. Az eltolódás mértéke annál nagyobb, minél kisebb a galaxisok látszólagos átmérője, illetve a látszólagos fényessége, vagyis minél nagyobb a távolságuk. Ezt az összefüggést írja le a Hubble-törvény. A legnagyobb vöröseltolódású extragalaxisok a kvazárok. Az eddig felfedezett legtávolabbi kvazár vöröseltolódása z = 6,28 az SDSS mérései alapján.
Csillagászati színképelemzés a gyakorlatban. Spektrográfok[szerkesztés]
Spektrográfok felépítése, tulajdonságai

Egy csillagászati spektrográf és egy laboratóriumban használt színképelemző berendezés között, bizonyos szempontból semmi, ugyanakkor mégis hatalmas különbségek vannak. A vizsgálni kívánt fény mindkét esetben hasonló utat fut be: legelőször áthalad egy résen, amely minden más zavaró fényforrást kizár, majd a divergens fénynyalábot a kollimátor párhuzamosítja, ezek után pedig a bontóelemre fókuszálja. A bontóelem (legtöbb esetben rács) a különböző hullámhosszú fénysugarakat különböző irányokba téríti el, előállítva ezzel a színképet. A spektrálisan bontott nyalábokat egy újabb optikai elem (kamera) vetíti a detektorra, aminek a síkjában így egymás mellé képződnek le a spektrum egyes tartományai. A detektor lehet fotolemez, vagy a legújabb technikának megfelelő CCD-mátrix.
A csillagászatban a vizsgálat tárgyát képező objektumok igen halványak, így egyetlen beérkező fotont sem szabad elveszítenünk a távcső által összegyűjtött fénynyalábból. Ez több feltételt is jelent a spektrográf felépítésére nézve. Például a rést kivilágító fénynyaláb a távcső optikájának megfelelően összetartó, majd a résen áthaladva széttartó fénykúpként jelentkezik. Ezt a kollimátornak maradéktalanul be kell fogadni, vagyis a kollimátor fényerejének nagyobbnak vagy egyenlőnek kell lennie a távcső fényerejével. A spektrográf egyik legfontosabb értékmérője a reciprok lineáris diszperzió: ennyire „húzza szét” a színképet; ezt ångström/mm-ben mérjük (1 nm = 10 A). A másik fontos tulajdonsága felbontóképesség, amely megadja, hogy egy adott hullámhosszon mekkora az a Δλ érték, amelyre két egymáshoz közel eső színképvonal még éppen szétválasztható. (R = λ/Δλ) A diszperzió és a felbontóképesség hasonló okoknál fogva nem azonos, mint a nagyítás és a felbontóképesség a vizuális távcsöves megfigyeléseknél. Ha két színképvonal egy λ hullámhossznál akkor választható szét, ha hullámhosszkülönbségük legalább Δλ, akkor a λ/Δλ arányt nevezzük felbontóképességnek. A legtöbb csillag halvány, ezért a felbontóképességnek és a diszperziónak is határa van. A legnagyobb diszperzió – viszonylag fényes csillagok esetében – kb. 1 A/mm. A felbontóképesség 500 nm-nél kb. 0,001 nm-t, esetleg valamivel kisebb értéket érhet el.
A felbontóképességet másképpen is kifejezhetjük: ahol R a rés mérete, m a spektrális rend száma, ρ a rácsállandó, λ a vizsgálandó fény hullámhossza, W a spektrográf optikájának átmérője, φ a rés mérete, DT a távcső átmérője (pontosan látszó szögátmérő).
A rés mérete meghatározza felbontóképességet, minél kisebb a mérete, annál nagyobb a felbontóképesség. Ugyanakkor viszont a rés méretének csökkenésével a spektrográfba jutó fény mennyisége is csökken, ami hátrányt jelent a halvány objektumok vizsgálatánál. Egy halvány csillag esetében ez nem engedhető meg, vagyis a rés méretének nagyobbnak vagy egyenlőnek kell lennie a csillag fókuszsíkbeli képénél. A rés méretét továbbá behatárolja a fényelhajlás (a távcső átmérője nem végtelenül nagy, a fény az objektív peremén elhajlást szenved) és a földi légkör. A fényelhajlás miatt a távcső a pontszerű csillag fényét nem egy végtelenül kicsi pontba, hanem egy kisméretű korongba és az azt körülvevő nagyon halvány gyűrűkbe vetíti (Airy-féle diffrakciós kép).
Optikai rács esetében a rácssorozat sűrűsége egyenesen arányos az elérhető felbontóképességgel: sűrűbb rács finomabb részleteket jelent. A rácsokat karcoló osztógépek azonban felső határt szabnak, a milliméterenkénti néhány ezer vonalnál nem lehetséges sűrűbb rácsot készíteni. Gyakorlatilag ρ = 1200 osztás/mm-nél sűrűbb rács nem fordul elő a csillagászati műszerekben. Efelett a határ felett ugyanis már jelentősen romlik a rácsok minősége, ami szórt fény megjelenéséhez vezet.
A spektrográfok fő típusai:
- Echelle-spektrográf
- Coudé-spektrográf
- Cassegrain-spektrográf
Az expozíciós időt befolyásoló tényezők:
- távcsőátmérő
- spektrográf hatékonysági foka
- CCD spektrális érzékenysége, kvantumhatásfoka
- égbolt háttérfényessége
A nagy felbontású spektrumok hosszabb expozíciós időt igényelnek, mivel a nagy felbontás fénysűrűség-csökkenéssel jár, ami hosszabb expozíciós időhöz vezet. Az expozíciós idő meghatározása a következőképpen történik:
Hullámhossz-kalibráció
A Doppler-effektusnak köszönhetően a színképben megfigyelhető vonalak a vörös vagy a kék hullámhossz felé tolódnak el, annak megfelelően, hogy a fényforrás távolodik, vagy közeledik felénk. Az eltolódás mértéke pedig a fényforrás sebességével arányos: Δλ / λ = v / c, ahol a Δλ a nyugvó rendszerbeli λ hullámhosszon megfigyelhető vonal eltolódása, v a fényforrás sebessége hozzánk viszonyítva, c pedig a fénysebesség. Az eltolódás Δλ értékének meghatározásához szükség van egy referenciára, ami a spektrumvonalak álló rendszerben megfigyelhető (laboratóriumbeli) pozícióit szolgáltatja. Fontos, hogy ez a referenciaforrás éles, jól elkülönülő vonalakkal rendelkezzen, lehetőleg a teljes vizsgálni kívánt spektrális tartományban. Erre az ún. spektrállámpát használják. Kisebb felbontóképességű spektrográfok esetén hélium-neon-argon gázzal töltött kisülési lámpákat alkalmaznak. Ezekben az anód és a valamilyen speciális fémmel bevont katód közötti magas feszültség ionizálja a lámpa töltésére használt gázt, ami így kisüléshez vezet az anód és a katód között. A nagy sebességgel katódba csapódó ionok a katód bevonatát adó fématomokat is kilökik, amik szintén ionizálódnak és fényt bocsátanak ki. Így a lámpa fényében egyszerre jelennek meg a gázra, és a katód bevonatára jellemző színképvonalak. Nagyobb felbontású műszerek esetén az argonnal töltött, tórium tartalmú katóddal rendelkező (ThAr) lámpákat használják referenciaként, mivel ezek szűk spektrális tartományon belül is számos vonallal rendelkeznek.
| Műszer | Teljes név | Teljes név magyarul | |
|---|---|---|---|
| AIRES | Airbone Infrared Echelle Spectrometer (SOFIA) | Airbone infravörös Echelle-spektrométer | |
| EUVE | Extreme Ultraviolet Explorer | Extrém ultraibolya kutató | |
| FLAMES | Fibre Large Array Multi Element Spectrograph (VLT) | ||
| FUSE | Far Ultraviolet Spectroscopic Explorer | Távoli ultraibolya spektroszkópiai megfigyelő | |
| GHRS | Goddard High-Resolution Spectrograph (Hubble űrtávcső) | Goddard nagy felbontású spektrográf | |
| GIRAFFE | Grating Instrument for Radiation Analysis with a Fibre Fed Échelle (VLT) | ||
| GMOS | Gemini Multi-Object Spectrograph (Gemini távcső) | Gemini multiobjektum-spektrográf | |
| NICMOS | Near Infrared Camera and Multi-Object Spectrograph (Hubble űrtávcső) | Közeli infravörös kamera és multiobjektum-spektrográf | |
Spektroszkópiai módszerek[szerkesztés]
I. Radiális sebesség mérések a Doppler-effektus felhasználásával. A színképelemzés felvilágosítást adhat egy égitest radiális (látóirányú) sebességéről. Ehhez a Doppler által felfedezett, és róla elnevezett Doppler-effektust használják fel. Ha egy fényforrás távolodik vagy közeledik tőlünk, akkor hullámhossz-eltolódást mutat a vörös ill. a kék felé. A Doppler-eltolódás legvilágosabban a színképvonalakon mutatkozik meg. Az eltolódás mértékéből meghatározható a vr radiális sebesség, a összefüggés alapján, ahol Δλ a λ hullámhossz megváltozása, c pedig a fénysebesség. Ennek alapján például megállapíthatjuk a Nap radiális sebességét, mégpedig a napkorong szélein mutatkozó Doppler-effektus segítségével. A radiális sebességre vonatkozó képletbe írjuk a Hα vonal hullámhosszát (λ = 641,0256 nm), és a színképelemzéskor megállapított (Δλ = ± 0,0043 nm) hullámhossz-eltolódását. Így a napkorong széleinek mozgási sebességére v = ± 2 km/s értéket kapunk. Az itt alkalmazott formula azonban csak a fénysebességnél jóval kisebb sebességek esetén érvényes! Ellenkező esetben relativisztikus effektusok lépnek fel: . Itt analógiát találhatunk a világegyetem tágulásával, mivel az égitestek egymástól való távolodás az okozója a kozmikus vöröseltolódás jelenségnek. A vöröseltolódás mértékét a z = Δλ / λ kifejezés adja meg.
II. Csillagok állapotjelzőinek meghatározása a gravitációs vöröseltolódás hatásaiból. Az általános relativitáselmélet egyik következménye, hogy egy nagy tömegű égitest felszínét elhagyó fény energiát veszít, vagyis a színképvonalak a vörös felé tolódnak el. A Δλ / λ ralatív eltolódás az égitest M tömegével egyenesen, R sugarával fordítottan arányos:
A gravitációs vöröseltolódás hatását nehéz más effektusoktól elválasztani, ennek ellenére a jelenség eredményesen alkalmazható a fehér törpék és a különösen nagy tömegű csillagok (Trümpler-csillagok) tömegének mérésére.
III. Baade-Wesselink-analízis. A radiális pulzációt (rezgéseket) mutató csillagok egyensúlyi sugarának meghatározására szolgáló módszer. A legegyszerűbb megvalósítása szerint a csillag színhőmérsékletének és fényességének változását mérve (fotometriával) következtethetünk a sugárváltozások arányaira, a pulzáló légkör sebességgörbéjét mérve pedig (spektroszkópiával megfigyelve) kiszámíthatjuk a sugár változásait hosszmértékben (km-ben). Végül a sugár két időpontban vett értékének hányadosa és különbsége adódik, amiből a csillag sugarát ebben a két időpontban meg lehet határozni.
IV. Doppler-imaging. A módszer alkalmas gyorsan forgó csillagok periódusidejének meghatározására és a heterogén fényességeloszlású csillagok felszínének feltérképezésére (csillagfoltok kimutatása). A forgó csillag különböző felületi pontjai különböző radiális sebességűek, különböző Doppler-eltolódásúak. A csillagfoltok – mivel kevés fény érkezik róluk – nem mutatnak abszorpciós színképvonalakat. A foltok pozíciójának megfelelő Doppler-eltolódású hullámhosszokon egy jellegzetes „púp” jelenik meg a színképvonal profiljában, ami a csillag forgása miatt végigvonul azon. Ennek elemzésével megállapítható a foltok elhelyezkedése. A módszer hátránya, hogy csak precíz vonalprofilok esetén alkalmazható.
V. Spektroszkópiai parallaxis. Meghatározott színképtípushoz (MKK-féle osztályozási rendszer) többé-kevésbé (általában kettes faktornál kisebb bizonytalansággal) meghatározott abszolút fényesség tartozik. Az egyéb spektrális paraméterek alapján az abszolút fényesség meghatározása tovább finomítható. Ezt összevetve a csillag látszó fényességével, meghatározhatjuk annak távolságát. Az ilyen módon kapott távolságot (vagy parallaxist) nevezzük spektroszkópiai parallaxisnak. Ennek meghatározásában további nehézséget jelent, hogy a G, K és M színképosztályú csillagok között vannak óriások és törpék is. A színképtípus tehát nem határozza meg egyértelműen az abszolút fényességet. Ehhez szükség van a luminozitási osztály megállapítására is, ami többek között meghatározható az adott csillag légkörében uralkodó nyomásból.
Kapcsolódó szócikkek[szerkesztés]
- Nap
- csillag
- spektroszkópia
- galaxis A galaxisok színképe
- Csillagászati színképosztályozás A színképosztályok definiálása, színképosztályozási rendszerek. A standardcsillagok listája ugyancsak itt található meg
- Hertzsprung–Russell-diagram Alapvető összefüggés a csillagok állapothatározói között
- Bohr-féle atommodell A Bohr-modellel magyarázható az égitestek vonalas színképe
- fény A látható elektromágneses sugárzás, a fény sebessége
- elektromágneses sugárzás A teljes elektromágneses színkép tartományairól részletesen
- Doppler-effektus
- fotometria (csillagászati fényességmérés) A színképelemzés mellett az asztrofizika másik legeredményesebb vizsgálati módszere
Jegyzetek[szerkesztés]
- ↑ http://uni-leipzig.de/~energy/pdf/freuse1.pdf
- ↑ Dieter B. Herrmann: Az égbolt felfedezői. Gondolat Kiadó, Budapest, 1981., p. 136. ISBN 963 280 982 3
Források[szerkesztés]
- Jacqueline Mitton: Cambridge Dictionary of astronomy
- A. David Thackeray: Astronomical spectroscopy
- J. Sz. Sklovszkij: Csillagok – születésük, életük, pusztulásuk
- Hebling János, Almási Tibor: Képalkotás és spektroszkópia THz-es sugárzással: a csillagászattól az orvosi alkalmazásokig. Magyar Tudomány 2005. 12. sz. ISSN 0025-0325 (teljes szöveg elérhető itt [1])
- Fűrész Gábor: Multiobjektum spektrográfia a modern csillagászatban. Természet Világa 2004. 4. sz. ISSN 0040-3717 (A folyóirat archívuma elérhető itt [2])
- Veszprémi Tamás–Nyulászi László: A fotoelektron-spektroszkópia alkalmazási lehetőségei és legújabb módszerei. Magyar Kémikusok Lapja 1997. 3. sz. ISSN 0025-0163 (52–53. évf. számai elérhetők itt [3])
- Vinkó József–Szatmáry Károly–Kaszás Gábor–Kiss László: A csillagok színképe. Meteor Csillagászati évkönyv 1998 (kiadja a Magyar Csillagászati Egyesület [4])
- The Messenger/El Mensajero 2002. december (Az ESO havonta megjelenő, interneten is elérhető kiadványa [5])
- Gázok és gőzök színképe, Bohr-posztulátumok, Franck-Hertz-kísérlet. A H-atom Bohr-modellje, Miskolci Egyetem
- Fűrész Gábor: CCD-kamerák a csillagászatban Archiválva 2022. január 19-i dátummal a Wayback Machine-ben
- https://web.archive.org/web/20060128003630/http://astro.u-szeged.hu/spectra/spektro5.html Vinkó József-Szatmáry Károly-Kaszás Gábor-Kiss László: A csillagok színképe, Meteor Csillagászati Évkönyvben, 1998
- Az SDSS honlapja
- AAOmega spektrográf, 2dF-rendszer Archiválva 2014. április 20-i dátummal a Wayback Machine-ben (angol)
- http://www.ast.cam.ac.uk./AAO/local/www/aaomega/Hectospec/Hectoechelle[halott link]
- Astronomical spectroscopy
- https://web.archive.org/web/20060408021458/http://www.astro.uiuc.edu/~kaler/sow/spectra.html Egy színes oldal a spektrumokról (angol)
- Spectroscopy, Durnhami Egyetem, Csillagászati Eszközök Csoportja
- Smithsonian Astrophysical Observatory, converted Multiple Mirror Telescope (angol)
- History of Astronomical Spectroscopy
- Astronomical spectroscopy and photometry
További információk[szerkesztés]
- Interaktív Flash animáció az emissziós és abszorpciós spektrumok érzékeltetésére a kozmokémiában. Szerző: Jason H. Dicker
















































