Vöröseltolódás

Vöröseltolódásnak hívjuk az elektromágneses hullámok hullámhosszának a kibocsátott hullámhosszhoz viszonyított megnövekedését. A jelenségnek a csillagászat és az asztrofizika területén fontos szerepe van, mivel a távoli galaxisok színképe a vörös felé tolódik. Az ellentétes jelenséget, amikor a hullámhossz rövidül, kékeltolódásnak hívjuk.
A vöröseltolódás három lehetséges okát meg kell különböztetni:
- a forrás és a megfigyelő relatív mozgása (Doppler-effektus, relativisztikus Doppler-effektus)
- a forrás és a megfigyelő gravitációs potenciálja eltérő (gravitációs vöröseltolódás)
- a Világegyetem tágulása (a forrás és a megfigyelő között)
Általában a vöröseltolódás (és a kékeltolódás, a kibocsátottnál rövidebb hullámhossz észlelése) a következő módon számszerűsíthető:
ahol a frekvencia és a hullámhossz.
Története[szerkesztés]
A tárgy története a hullámmechanika 19. századi kifejlesztésével és a Doppler-effektussal kapcsolatos jelenségek felfedezésével kezdődött. A jelenséget Christian Andreas Dopplerről nevezték el, aki 1842-ben az első ismert fizikai leírását adta a jelenségnek[1] A feltevést a holland Christoph Hendrik Diederik Buys Ballot tesztelte 1845-ben hanghullámok segítségével, és megállapította annak helyességét.[2] Doppler helyesen állapította meg, hogy a jelenségnek mindenféle hullám esetén létre kell jönnie, és azt is felvetette, hogy a csillagok különböző színe is a Földhöz viszonyított mozgásukból ered.[3] Bár ez utóbbi megállapítás helytelennek bizonyult (a csillagok színe a csillag hőmérsékletével kapcsolatos, nem a mozgásával), a Doppler-effektust igazolták a vöröseltolódás megfigyelésével.
Az első Doppler-féle vöröseltolódást 1848-ban egy francia fizikus, Armand-Hippolyte-Louis Fizeau írta le, aki kimutatta a csillagok színképének eltolódását a Doppler-effektusnak megfelelően. A hatást emiatt Doppler–Fizeau-hatásnak is nevezik. 1868-ban William Huggins brit csillagász volt az első, aki ezzel a módszerrel először határozta meg egy a Földtől távolodó csillag sebességét.[4]
1871-ben a Nap forgásával kapcsolatosan állapították meg a jelenség létezését a Fraunhofer-vonalak megfigyelésével, az eltolódás nagyjából 0,1 Å volt.[5] 1901-ben Aristarh Apollonovics Belopolszkij mért optikai vöröseltolódást laboratóriumban, forgó tükrökből álló rendszer segítségével.[6]]
A vöröseltolódás kifejezés először Walter S. Adams amerikai csillagász cikkében jelent meg nyomtatásban 1908-ban ("Two methods of investigating that nature of the nebular red-shift".)[7] Maga a szó idézőjelek nélkül csak 1934-ben jelenik meg Willem de Sitter által használva.[8]
1912-ben kezdett észleléssorozatában Vesto Slipher felfedezte, hogy a legtöbb spirálködnek jelentős vöröseltolódása van.[9] Ezután Edwin Hubble felfedezett egy közelítő kapcsolatot az ilyen „ködök” (akkor még nem tekintették csillagvárosoknak, galaxisoknak) vöröseltolódása és a távolságuk között, amely a Hubble-törvényhez vezetett[10] Ezek a megfigyelések megerősítették Alexander Friedmann 1922-es munkáját, melyben levezette a Friedmann-egyenleteket.[11] Ezek ma a táguló világegyetem és az Ősrobbanás-elmélet komoly bizonyítékát jelentik.[12]

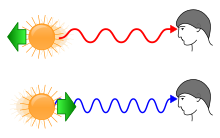
1: a fényforrás elmozdulásának hatására az elmozdulással ellentétes irányban a fényhullámok megnyúlnak
2: a fényforrás elmozdulási iránya
3: fényforrás
4: a fényforrás mozgása miatt a szemben lévő megfigyelőhöz érkező fény hullámhossza lerövidül
A jelenség okai[szerkesztés]
A vöröseltolódásnak a következő okai lehetnek:
A forrás mozgása[szerkesztés]
Ha a fényforrás távolodik a megfigyelőtől, akkor vöröseltolódás () lép fel; ha a forrás a megfigyelő felé mozog, akkor pedig kékeltolódás (). Ez minden hullám esetén igaz, és a Doppler-effektussal magyarázható. Ha a forrás a megfigyelőtől a fény sebességénél jóval kisebb sebességgel távolodik, akkor a vöröseltolódás megadható a
összefüggéssel, ahol a fénysebesség.
Fontos hangsúlyozni, hogy a kifejezés csak közelítő, és a fénysebesség közelében módosításra szorul (relativisztikus Doppler-effektus):
A tér tágulása[szerkesztés]

A kozmológia jelenleg elfogadott modellje szerint a tér tágul, és a fény hullámhossza megnövekszik (megnyúlik) a tér tágulásával, ami a fény vörösebbé válásaként látszik látható fény esetében. Ha a Világegyetem az összehúzódás állapotában lenne, akkor a távoli galaxisok fénye a kék felé tolódna. A távoli galaxisok vöröseltolódása teljesen úgy látszik, mintha a távoli galaxisok távolodnának, az általános relativitáselmélet szerint viszont a távolodás, és a tér tágulása két különböző dolog. A távoli galaxisokra ne úgy tekintsünk, mint amelyek távolodnak, hanem úgy, hogy a közöttünk levő tér tágul. Ennek ellenére néha hivatásos csillagászok is kissé pongyolán „távolodási sebességről” beszélnek a vöröseltolódás esetében, ami a laikusokat megzavarhatja.
Gravitációs hatások[szerkesztés]
Az általános relativitáselmélet szerint az erős gravitációs téren keresztülhaladó fény vörös vagy kékeltolódást szenvedhet. Ezt Einstein-eltolódásként ismeri a szakirodalom. Ez a hatás a Földön nagyon kicsi, de a Mössbauer-effektus révén mérhető. Ennek ellenére a fekete lyuk esetén nagyon jelentős: azoknak a testeknek, melyek elérik az eseményhorizontot, a vöröseltolódása végtelenné válik. Ez a fő oka a kozmikus mikrohullámú háttérsugárzás nagy szögskálájú hőmérséklet-ingadozásainak is.
Megfigyelése[szerkesztés]
A Doppler-effektus csillagászati alkalmazásait a Doppler-effektus szócikkben találhatjuk. A továbbiakban a másfajta eredetű vöröseltolódásokról írunk.
A csillagászat területén a vöröseltolódás mérhető, hiszen az atom emissziós és abszorpciós (elnyelési) színképe jól ismert. Amikor távoli galaxisok színképét vizsgáljuk, akkor a megfelelő színképvonalak a kisebb frekvenciák (nagyobb hullámhosszak) felé tolódnak el. Minél távolabbi egy objektum, annál nagyobb a vöröseltolódása. Ezekre a távolabbi objektumokra úgy is tekinthetünk, mint amelyek korábbi állapotúak, ugyanis a fénynek időre van szüksége, hogy hozzánk eljusson. A legnagyobb megfigyelhető vöröseltolódása a kozmikus mikrohullámú háttérsugárzásnak van: z = 1089. Ez időben a jelenleginél 13,7 milliárd évvel korábbnak felel meg, és az Ősrobbanás utáni 379 000. évnek.
A Lokális Csoporton kívüli, de ezer megaparszeknél közelebbi galaxisok esetén a vöröseltolódás a galaxis távolságával arányos, amelyet Edwin Hubble fedezett fel, és róla Hubble-törvénynek nevezték el. Ezt az eltolódást a tér tágulásának a számlájára írják, azaz minél távolabb van egy galaxis, annál nagyobb mértékben tágult a tér, mióta a fénye elért minket, azaz annál jobban megnyúlt a fény hullámhossza, annál jobban eltolódott a hullámhossza a vörös felé, annál nagyobb sebességgel látszik távolodni. A vöröseltolódás gyakran könnyebben és pontosabban mérhető, mint a távolodási sebesség, ezért a távolságot általában a vöröseltolódásból számolják a Hubble-törvény szerint.
A még távolabbi galaxisok esetén a jelenlegi távolság és a megfigyelt vöröseltolódás közötti összefüggés bonyolultabbá válik. Ha valaki egy távoli galaxist néz, akkor annak egy régmúltbeli állapotát figyeli meg, amikor a Világegyetem másmilyen volt, mint most. Úgy feltételezzük, hogy régebben más sebességgel tágult a Világegyetem, mint most. A feltételezésnek két oka van: (1) a gravitációs vonzás hatására a tágulásnak lassulnia kell és (2) a kozmológiai állandó jelenléte változtathatja a világegyetem tágulási ütemét. Jelenlegi megfigyeléseink viszont arra utalnak, hogy a világegyetem tágulása nem lassul, ahogy (1) szerint várjuk, hanem gyorsul.
A táguló Világegyetem az Ősrobbanás-elmélet alapvető következménye.
Működése[szerkesztés]
Egy egyszerű foton a vákuumbeli terjedése során többféle módon is képes vöröseltolódásra. Ezek mindegyike a Doppler-jelenséghez hasonló, ami azt jelenti, hogy független a hullámhossztól. Ezeket a Galilei-transzformációval, Lorentz-transzformációval, vagy az általános relativitáselmélet segítségével írhatjuk le.
| Eltolódás típusa | Eltolódási törvény | Példa téridők[13] | Definíció[14] |
|---|---|---|---|
| Doppler-eltolódás | Galilei-transzformáció | Newtoni téridő | |
| Relativisztikus Doppler | Lorentz-transzformáció | Minkowski téridő | |
| Kozmológiai vöröseltolódás | általános relativitáselmélet | FRW téridők | |
| Gravitációs vöröseltolódás | általános relativitáselmélet | Schwarzschild téridő |
Jegyzetek[szerkesztés]
- ↑ Doppler, Christian, "Beitrage zur fixsternenkunde" (1846), Prag, Druck von G. Haase sohne
- ↑ Dev Maulik, "Doppler Sonography: A Brief History" in Doppler Ultrasound in Obstetrics And Gynecology (2005) by Dev (EDT) Maulik, Ivica Zalud
- ↑ John J. O'Connor és Edmund F. Robertson. Vöröseltolódás a MacTutor archívumban. (angolul)
- ↑ William Huggins, "Further Observations on the Spectra of Some of the Stars and Nebulae, with an Attempt to Determine Therefrom Whether These Bodies are Moving towards or from the Earth, Also Observations on the Spectra of the Sun and of Comet II." (1868) Philosophical Transactions of the Royal Society of London, Volume 158, pp. 529–564
- ↑ Reber, G., "Intergalactic Plasma"(1995) Astrophysics and Space Science, v. 227, p. 93–96.
- ↑ Bélopolsky, A., "On an Apparatus for the Laboratory Demonstration of the Doppler-Fizeau Principle" (1901) Astrophysical Journal, vol. 13, p.15
- ↑ Adams, Walter S., "No. 22. Preliminary catalogue of lines affected in sun-spots" (1908) Contributions from the Mount Wilson Observatory / Carnegie Institution of Washington, vol. 22, pp.1–21
- ↑ W. de Sitter, "On distance, magnitude, and related quantities in an expanding universe, (1934) Bulletin of the Astronomical Institutes of the Netherlands, Vol. 7, p.205. He writes: "It thus becomes urgent to investigate the effect of the redshift and of the metric of the universe on the apparent magnitude and observed numbers of nebulae of given magnitude"
- ↑ Slipher first reports on his measurement in the inaugural volume of the Lowell Observatory Bulletin, pp.2.56-2.57 [1]. His article entitled The radial velocity of the Andromeda Nebula reports making the first Doppler measurement on September 17, 1912. In his report, Slipher writes: "The magnitude of this velocity, which is the greatest hitherto observed, raises the question whether the velocity-like displacement might not be due to some other cause, but I believe we have at present no other interpretation for it." Three years later, in the journal Popular Astronomy, Vol. 23, p. 21–24 [2], Slipher wrote a review entitled Spectrographic Observations of Nebulae. In it he states, "The early discovery that the great Andromeda spiral had the quite exceptional velocity of - 300 km(/s) showed the means then available, capable of investigating not only the spectra of the spirals but their velocities as well." Slipher reported the velocities for 15 spiral nebulae spread across the entire celestial sphere, all but three having observable "positive" (that is recessional) velocities.
- ↑ Hubble, Edwin, "A Relation between Distance and Radial Velocity among Extra-Galactic Nebulae" (1929) Proceedings of the National Academy of Sciences of the United States of America, Volume 15, Issue 3, pp. 168–173 (Full article Archiválva 2008. június 30-i dátummal a Wayback Machine-ben, PDF)
- ↑ Friedman, A: Über die Krümmung des Raumes, Z. Phys. 10 (1922), 377–386. (English translation in: Gen. Rel. Grav. 31 (1999), 1991–2000.)
- ↑ This was recognized early on by physicists and astronomers working in cosmology in the 1930s. The earliest layman publication describing the details of this correspondence was Sir Arthur Eddington's book The Expanding Universe: Astronomy's 'Great Debate', 1900–1931, published by Press Syndicate of the University of Cambridge in 1933.
- ↑ Létezhetnek más téridők is a megfelelő vöröseltolódásokra. Főképp a gravitációs vöröseltolódásra
- ↑ Ahol = vöröseltolódás; = sebesség; = fénysebesség; = Lorentz-factor; = skálafaktor; = gravitációs állandó; = test tömege; = Schwarzschild-sugár
További információk[szerkesztés]
- Magyarított Java szimuláció a kozmológiai vöröseltolódásról. Szerző: Fu-Kwun Hwang




















