Gravitációs állandó
A gravitációs állandó egy természeti állandó, mint például a fény terjedési sebessége vákuumban vagy az elemi töltés, azaz az elektron töltése. Nagyságának minél pontosabb meghatározása alapvető jelentőségű a tudomány számára. Értéke SI egységben a CODATA 2018-as ajánlása alapján:[1]
Az általános tömegvonzás törvénye és a gravitációs állandó[szerkesztés]

A klasszikus mechanikában az általános tömegvonzás törvénye szerint két test között ható vonzóerő egyenesen arányos a két test tömegével és fordítottan arányos a köztük lévő távolság négyzetével:
Az összefüggésben szereplő arányossági tényező, melyet -val, vagy f -fel (vagy G -vel) jelölnek, a gravitációs állandó. De nevezik az általános tömegvonzás állandójának és Newton-állandónak is.
A gravitációs kölcsönhatás két hétköznapi méretű tárgy között nagyon kicsi. Például két 1 kg-os, egymástól 1m távolságban lévő test között 6,7·10−11 N. Ráadásul nagyon nehéz az egyéb zavaró hatások kiküszöbölése, ezért kimutatása és az együttható mérése nem egyszerű feladat. Ma is az egyik legbizonytalanabbul meghatározható fizikai állandó.
A gravitációs állandó, Newton és Cavendish[szerkesztés]
Maga Newton nem írta fel a fenti összefüggést így. A Principiában 1687-ben a gravitációs törvény megfogalmazásakor arányosság formájában adta meg, hogyan függ az erő a két test tömegétől és távolságától. Nem vezetett be, és így nem is mért meg semmilyen együtthatót.
Még Cavendish idején sem volt ismert a számunkra már teljesen megszokott fenti képlet. Híres kísérletében és publikációjában 1798-ban Cavendish a mérési adatokból a Föld sűrűségét számolta ki és adta meg.[2]
Cavendish kísérlete[szerkesztés]

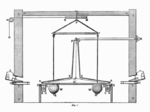
Vagy száz évvel a törvény felfedezése után vált lehetővé először Cavendish torziós ingával kivitelezett kísérlete révén egyáltalán a gravitációs vonzóhatás kimutatása.
Torziós ingát először Coulomb készített. A Francia Tudományos Akadémiához beadott– egy iránytű megalkotását célzó – pályamunkában írta le a torziós mérleget 1784-ben. Felismerte, hogy egy vékony szál - adott nagyságú forgatónyomaték hatására bekövetkező - elfordulása fordítottan arányos a szál átmérőjének negyedik hatványával. Tehát a kicsi erő hatására létrejövő forgatónyomaték is képes könnyebben észlelhető nagy elfordulást létrehozni, ha elég vékony a szál. Így nagyon kicsiny hatás kimutatására is alkalmas eszközt talált fel.[3]
Ezen ötlet alapján John Michell természetfilozófus és geológus épített egy a Föld átlagos sűrűségének meghatározására tervezett elrendezést. A kísérletet azonban már Cavendish végezte el.[4][5] A műszer egy torziós huzalra felfüggesztett, 1,8 m hosszú farúdból állt, aminek két végén egy-egy 5 cm átmérőjű ólomgolyó (m) volt. A két golyó mellé, kis távolságra egy-egy 160 kilogrammos ólomgömböt (M) függesztett úgy, hogy azok maguk felé vonzották a kisebb golyókat, ezzel az ingát elfordítva, a torziós szálat elcsavarva. Hogy elkerülje a légáramlatok zavaró hatását, Cavendish a roppant érzékeny berendezést huzatmentes helyiségben állította fel, azon belül is egy vastag falú, 3 méteres zárt fadobozban, és az inga elfordulását csak egy kis, beépített távcsővel figyelte meg.
A mérleg csupán 4,1 mm-elfordulásából és a kalibrált torziós huzalban az elfordulás hatására ébredő csavarónyomatékból ki lehetett számolni a kis és nagy gömb között létrejövő erőt, amely mindössze 1,47•10−7 N-nak, vagyis egy tízmilliomod newton nagyságrendűnek bizonyult, ez körülbelül egy nagyon finom porszemcse súlya. Cavendish nagyon részletesen és alaposan dokumentálta a kísérletet. A Föld átlagsűrűségére – a vízéhez viszonyítva – az 5,448-szoros értéket adta meg. Utólag megállapítható, hogy a mérési adataiból a gravitációs állandóra a
értéket kapta volna.[6]
Cavendish és a gravitációs állandó mérése kétszáz éven keresztül[szerkesztés]
A tömegvonzás jelenségének demonstrálására ma is a Cavendish-féle torziós ingát használjuk. A kísérletet amerikai tudósok a 10 legszebb közé sorolták, az interneten több szemléltető animáció is elérhető róla.[7]
Nagyjából kétszáz éven keresztül Cavendish mérési módszere alapján mérték a tudósok a Newton-állandó értékét. A sztatikus módszer pontosságának kulcsa, hogy a vonzóhatásból származó forgatónyomaték és az elfordulás szöge között lineáris legyen a kapcsolat. Ez csak a szál tökéletesen rugalmas volta esetén valósul meg elvileg. Pontatlanság forrása még, hogy az ingára helyezett tömegek kiterjedése nem hanyagolható le, hogy sűrűségeloszlásuk nem eléggé homogén. Az újabb és újabb kísérletek során egyre jobb minőségű torziós szálakat, és egyre jobb szögelfordulás leolvasási technikákat alkalmaztak.
Eötvös Loránd a gravitációval foglalkozó tanulmányai során nem csak a földi nehézségi gyorsulás nagyon pontos mérési módszerét adta meg, de egy a korábbiaktól eltérő megoldást javasolt a gravitációs állandó mérésére is.[8] Módszerének lényege az volt, hogy nem magát a gravitációs kölcsönhatást, hanem annak változását figyelte meg. A nagyon alapos elméleti elgondolások és ennek megfelelően tervezett gondos kísérleti elrendezés ellenére nem sikerült lényegesen nagyobb pontosságot elérnie, mint elődeinek. De az utána következő mérésekben követték az ötletet, a felfüggesztett súlyok a vonzó tömegek hatására oszcillálnak. A vonzó tömegek helyzetének megváltoztatása után a felfüggesztett súlyok egy újabb egyensúlyi helyzet körül, más frekvenciával oszcillálnak. A frekvencia megváltozásából lehet következtetni a gravitációs állandóra.
Mindezen statikus gravitációsállandó-mérési módszerek akármilyen javítgatásával sem lehet azonban megközelíteni a fénysebesség vagy más fontos természeti állandók mérésének pontosságát.
Az újabb dinamikus mérési módszer[szerkesztés]
Az 1990-es években jelentek meg a dinamikus mérési módszerek, amelyek kiküszöbölhetik a korábbi hibaforrásokat, és új lehetőséget jelenthetnek a gravitációs állandó mérési hibájának lényeges csökkentésére.
Az amerikai University of Washington egyetemen működik egy kutatócsoport, akik Eötvös Loránd iránti tiszteletből Eöt-Wash csoportnak nevezik magukat.[9] Fő kutatási területük a gyenge gravitációs mezővel kapcsolatos mérések és új, a gravitációsnál gyengébb kölcsönhatások felkutatása.
Elrendezésükben a torziós szálra felfüggesztett, a torzióban részt vevő elemet egy vékony síklapra cserélték, aminek mind a méretéből, mind a sűrűségeloszlásából származó eltérés jól figyelembe vehető. Ezzel a síklappal több, szimmetrikusan elhelyezett vonzógömb hat kölcsön, amik egy forgótányéron vannak rögzítve. A kísérlet során az inga és a forgótányér visszacsatolással összehangolt forgásának szögsebességét mérik az időben. A módszer kiküszöböli a torziós szál nem tökéletes rugalmasságból származó hibát is. A 2000-ben megjelent publikációjuk óta is folyamatosan fejlesztik a kísérletet. Mostanára a CODATA által vizsgált sok-sok mérési adat között meghatározó az általuk a gravitációs állandóra megadott érték, mind a nagyságát, mind a relatív standard hibáját tekintve.[10]
Jegyzetek[szerkesztés]
- ↑ http://physics.nist.gov/cgi-bin/cuu/Value?c%7Csearch_for=universal_in!
- ↑ Experiments to Determine the Density of Earth (Philosophical Transactions of the Royal Society of London, volume 88)
- ↑ Simonyi Károly: A fizika kultúrtörténete, Gondolat Kiadó, Budapest, 1981)
- ↑ http://www.public.iastate.edu/~lhodges/Michell.htm Archiválva 2017. szeptember 6-i dátummal a Wayback Machine-ben)
- ↑ Isobel Falconer: Henry Cavendish: the man and the measurement, Meas. Sci. Technol. 10 (1999) 470–477
- ↑ Mann, Adam (2016. szeptember 6.). „The curious case of the gravitational constant” (angol nyelven). Proceedings of the National Academy of Sciences 113 (36), 9949–9952. o. DOI:10.1073/pnas.1612597113. ISSN 0027-8424.
- ↑ Archivált másolat. [2012. június 18-i dátummal az eredetiből archiválva]. (Hozzáférés: 2014. november 8.)
- ↑ Eötvös Loránd: Vizsgálatok a gravitatio és a mágnesség köréből, Mathematikai és Természettudományi Értesítő XIV. köt. 4. füzet, 1-46, 1896
- ↑ http://www.npl.washington.edu/eotwash/
- ↑ J. H. Gundlach, S. M. Merkowitz: Measurement of Newton’s Constant Using a Torsion Balance with Angular Acceleration Feedback, Phys. Rev. Lett., Volume 85, Number 14 (2000)




