Logaritmus
A logaritmus két szám között értelmezett matematikai művelet, amely közeli kapcsolatban van a hatványozással. A pozitív b szám a alapú logaritmusán (ahol a egytől különböző pozitív szám) azt a kitevőt értjük, melyre a-t emelve b-t kapjuk.[1] Például 1000-nek 10-es alapú logaritmusa 3, mert 10 harmadik hatványa 1000.
A b szám a alapú logaritmusát
jelöli, amely tehát az egyetlen valós szám, amelyre
Például , ugyanis, ha a 81-et a logaritmus alapjának, azaz a 3-nak hatványaként írjuk fel, akkor a kitevő 4 lesz:
A logaritmus képzése a gyökvonáshoz hasonlóan egy bizonyos értelemben a hatványozás megfordítása,[2] de amíg a gyökvonás az összefüggés alapján az eredmény és a kitevő ismeretében keresi az alapot, addig a logaritmus az eredmény és az alap ismeretében a kitevőt határozza meg.[3]
A logaritmust John Napier vezette be a 16. század végen, hogy megkönnyítse a szorzást, hatványozást tartalmazó számolásokat. Az elnevezés a görög „λόγος” (logosz, arány) és „ἀριθμός” (arithmosz, szám) szavak összetételéből származik. A számítások megkönnyítésére logarléceket és logaritmustáblázatokat készítettek, amelyek hamarosan elterjedtek a tengerészetben, a tudományokban és a mérnökök között. Ezek az eszközök a logaritmus azonosságait használják fel. A logaritmus mai jelölése Leonhard Eulertől származik, aki elsőként kapcsolta össze az exponenciális függvénnyel.
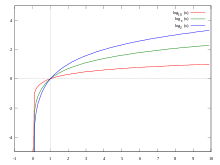
A 10-es alapú logaritmust a természettudományokban és a mérnöki tudományokban használják. Jelölése: . A természetes logaritmus alapja az e Euler-konstans (Euler-féle szám), és a matematikában széleskörűen alkalmazzák. Jelölése (matematikai szakszövegekben sokszor ). A 2-es alapú logaritmust a számítástudományban és az informatikában alkalmazzák. Jelölése egyszerűen , az alap kiírása nélkül. Német nyelvterületen erre az jelet használják.
A logaritmikus skálák kis tartományon széles tartományú mennyiségeket képesek ábrázolni. Így működik például a látás és a hallás. A decibel egy olyan viszonylagos egység, ami teljesítmények, vagy amplitúdók arányainak logaritmusát méri.[4] A kémiában a pH a vizes oldatok kémhatását méri. A földrengések nagyságát is logaritmikus skálában mérik. A bonyolultságelméletben is megjelennek, például az összehasonlításos rendezések bonyolultsága legalább .
Az általánosan használt logaritmusfogalom tehát a pozitív valós számok körében érvényes, de kiterjeszthető a negatív és a komplex számokra is. A valós számokon a logaritmus – rögzített alap esetén – a hatványozás inverz művelete. Ez megmarad a komplex számok fölött is. Egy másik változat a diszkrét logaritmus, amit a kriptográfiában is használnak.
Jellemzés[szerkesztés]
Ahogy a logaritmus definíciója is mutatja, a pozitív számokon értelmezett (egytől különböző, pozitív alapú)
függvény az a alapú exponenciális függvény inverze (egészen pontosan a képlet szerint a jobbinverze), vagyis az jelölést alkalmazva minden pozitív x számra
- .
Emellett a logaritmusfüggvény balinverze is az a alapú exponenciális függvénynek:
- .[5]
Eszerint a logaritmus művelete a következő eljárással állítja elő a kimenetét. A az az utasítás, mely az x pozitív számot felírja az a alap valahányadik hatványaként, majd ennek a hatványnak a kitevőjét leolvassa és ezt adja értékül a kifejezésnek:
Például log101000 = 3, log10100000 = 5, log101 000 000 000 = 9, illetve log1010n = n. A tízes alapú logaritmus tehát „a 0-kat számolja meg”. Így az A szám számjegyeinek száma 10-es számrendszerben az szám egészrésze. Általában c-es számrendszerben felírt A szám számjegyeinek száma: egészrésze.
Alternatív definíciók[szerkesztés]
Egy alternatív definíció a logaritmus azonosságaira támaszkodik, de hatványsorával és a természetes logaritmus az integráljaként is definiálható, amiből a többi logaritmus az alap megváltoztatására szolgáló képlettel kapható. Ez az utóbbi két definíció nem vonatkoztatható a diszkrét logaritmusra.
- A logaritmus egy izomorfiasereg, és más ilyen izomorfia nincs.
- A természetes logaritmus az integrállal kapható, ha t > 0.
- A logaritmus hatványsora: .
Mindezekről az összefüggésekről alább bővebben is szót ejtünk.
Jelölésrendszer[szerkesztés]
A számításokban leggyakrabban a tízes és a kettes alapú logaritmust, valamint az e alapú ún. természetes logaritmust használják. Ezek jelölésére országonként és tudományáganként különböző rövidítések használatosak.
Magyarországon a 10-es alapú logaritmust leggyakrabban
jelöli (például középiskolai tankönyvekben is).[7] Az angolszász mintára készült számológépeken a tízes alapú logaritmus jele log(x). A tízes alapú logaritmust még közönséges logaritmusnak is nevezik. Kézi számolásokhoz egyszerű használni a tízes számrendszerhez való alkalmazkodás miatt:[8]
Így a 10-es alapú logaritmus kapcsolódik a decimális jegyek számához: a számjegyek száma az a legkisebb egész, ami szigorúan nagyobb a szám 10-es alapú logaritmusánál.[9] Például . A következő egész a 4, ami valóban megegyezik a számjegyek számával. A függvénytáblázatból a logaritmus törtrésze, a mantissza olvasható ki; a karakterisztikát a felhasználónak kell megadnia a szám nagyságrendje alapján. Általában egy számrendszerben a szükséges számjegyek száma aszimptotikusan egyenlő a szám megfelelő alapú logaritmusával.
A másik gyakran használt logaritmus a természetes logaritmus, aminek az alapja az Euler-féle szám, az e. Ennek jele általában
- ,
ami a latin „logarithmus naturalis” (természetes logaritmus) kifejezés rövidítése. Gyakran azonban, főleg a számítástudományban log(x) jelöli a természetes logaritmust, míg a tízes alapút log10(x). A matematikai analízisben széleskörűen használják kellemes analitikai tulajdonságai miatt. Elterjedt a statisztikában, a gazdaságtani elméletekben, a fizikában, kémiában és egyes mérnöki alkalmazásokban is.
A kettes alapú logaritmust az információelméletben[10] és a számítógép-tudományban használják, alkalmazkodva a kettes számrendszerhez. Az információelméletben a természetes logaritmus is előfordul.[10] A zeneelméletben szintén eleve adva van a kettes alap, mivel egy hang és oktávjának frekvenciájának aránya 2. A cent két szomszédos, egyenletesen temperált hang frekvenciájának arányának logaritmusa 1200-zal szorozva. A fényképészetben az expozíciós időt mérik kettes alapú logaritmikus skálán.[11]
Tulajdonságok[szerkesztés]
Alakja:[5]
Összefüggések[szerkesztés]
A logaritmusfüggvény művelettartó leképezés a pozitív számok szorzással ellátott halmaza és a valós számok összeadással ellátott halmaza között. Az algebra szaknyelvén ez azt jelenti, hogy a függvény izomorfizmus a és az csoport között. A szorzásból összeadást csinál, az osztásból kivonást, az 1-ből 0-t. Mondhatjuk, hogy a logaritmus függvény a hatványozást szorzásra, a szorzást összeadásra vezeti vissza. Tetszőleges a pozitív, nem 1 számra és x, y pozitív számra:[5]
Az azonosságok a logaritmus vagy definíciójából helyettesítéssel származtathatók.[5]
Az összeg és a különbség logaritmusára ismert azonosság nem könnyíti meg a számolást:
tehát
Bármely logaritmus visszavezethető egy tetszőleges másik alapra:
A különböző alapú logaritmusfüggvények tehát egymás konstansszorosai.
A tudományos számológépek általában csak 10-es vagy természetes logaritmust tudnak számolni.
Egy adott x pozitív számnak még a logaritmusa is ismert egy ismeretlen b-re, akkor a b szám így számítható:
Analitikai tulajdonságok[szerkesztés]
A logaritmus mélyebb tanulmányozása a függvény fogalmára támaszkodik. Ez egy olyan reláció, ami értelmezési tartományának minden eleméhez hozzárendel egy, és csakis egy értéket.[13] Ezekből az értékekből áll a függvény értékkészlete.[14] A valós logaritmus, mint függvény a pozitív számokon értelmezett, és értéke befutja a teljes valós számkört.
Ahhoz, hogy a logaritmusfüggvény jóldefiniált legyen, meg kell mutatni, hogy a
egyenlet megoldható, és megoldása egyértelmű, ha b és y is pozitív, és b nem egyenlő eggyel. Ez a Bolzano-tétellel bizonyítható.[15] Eszerint egy folytonos függvény nem ugorhat át egy értéket; ha azon az intervallumon, ahol folytonos, felveszi az a és a b értékeket, akkor minden olyan értéket felvesz, ami a és b között van.
Ez megmutatható az függvényre a fenti kikötésekkel. Mivel f akármilyen kicsi és akármilyen nagy pozitív értékeket is felvesz, így minden y > 0 számhoz található és alkalmas x0-ra és x1-re. Emiatt a Bolzano-tétel szerint megoldható. Továbbá, mivel f szigorúan monoton nő, ha b 1-nél nagyobb, és szigorúan monoton csökken, ha b 1-nél kisebb, a megoldás egyértelmű.[16]
Ez az egyértelmű megoldás y b alapú logaritmusa, . A fenti kikötéseknek megfelelő b-vel, mint alappal az y-hoz annak logaritmusát hozzárendelő függvény a logaritmusfüggvény, vagy logaritmus.[17]
A függvény alapvető jellemzője a fenti szorzatképlet:
Pontosabban, ha b > 1, akkor a logaritmus az egyetlen monoton növő függvény, ami eleget tesz az f(b) = 1 és függvényegyenlet-rendszernek.[18]
Inverz függvény[szerkesztés]

A hatvány logaritmusára vonatkozó képlet alapján minden x számra
Szavakkal: a b alapot x-edik hatványra emelve és ennek b alapú logaritmusát véve visszakapjuk a b számot.
Megfordítva, ha y pozitív szám, és
akkor először a logaritmust véve és erre emelve az alapot visszakapjuk az y számot. Tehát bármelyik műveletet végezzük előbb és a másikat később, mindannyiszor visszakapjuk az eredeti számot. Emiatt a b alapú logaritmus a b alapú hatványfüggvény inverz függvénye.[19]
Az inverz függvények közeli kapcsolatban állnak az eredeti függvénnyel. Grafikonjuk megkapható az x és az y koordináták felcserélésével, azaz az x = y egyenesre való tükrözéssel. A hatványfüggvény grafikonjának (t, u = bt) pontja az (u, t = logbu) pontot adja a logaritmus grafikonján, és megfordítva. Emiatt logb(x) tart a végtelenbe, ha x tart a végtelenbe, hogyha b nagyobb 1-nél. Ekkor logb(x) monoton nő. Ha b < 1, akkor a logb(x) függvény a mínusz végtelenhez tart. Ha x a nullához tart, és b > 1, akkor a logaritmus a mínusz végtelenhez tart; ha pedig b < 1, akkor végtelenhez tart.[17]
Derivált és primitív függvény[szerkesztés]

A függvények egyes analitikai tulajdonságai átvihetők az inverz függvényre.[15] Ilyen tulajdonság a folytonosság és a differenciálhatóság. Így, mivel deriválható, ezért is differenciálható. Szavakkal: egy folytonos függvény ott deriválható, ahol nincs töréspontja. Továbbá, mivel deriváltja az exponenciális függvény tulajdonsága alapján, ezért a láncszabály szerint deriváltja:[16][20]
Így a b alapú logaritmusfüggvény pontbeli érintőjének meredeksége . Továbbá deriváltja , eszerint határozatlan integrálja . Az általánosított függvény argumentummal:[21]
A jobb oldalon álló hányados logaritmikus deriváltja. Az derivált kiszámítása felhasználásával logaritmikus differenciálás néven ismert.[22] Az primitív függvénye:[23]
Más alapú logaritmusokra a logaritmus alapváltásával egy szorzótényező jelenik meg.[24]
A természetes logaritmus mint integrál[szerkesztés]

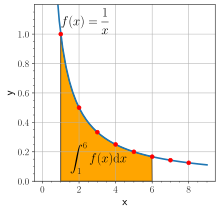
Ha t pozitív, akkor a természetes logaritmusa megegyezik 1/x dx integráljával 1-től t-ig:
Más szavakkal, megegyezik az x tengely és az 1/x grafikonja között 1-től t-ig terjedő területtel. Ez az analízis alaptételének és annak a következménye, hogy deriváltja 1/x. Az egyenlet jobb oldala a természetes logaritmus definíciója lehet. A logaritmus szorzásra és hatványozásra vonatkozó összefüggései is származtathatók ebből.[25] Például az szorzatképlet:
Az első egyenlet két részre osztja az integrált, míg a második elvégzi az helyettesítést. A bal oldali területet felfelé megnyújtjuk t-szeresére, és vízszintesen összenyomjuk t-edrészére, akkor a terület területe változatlan. Megfelelően eltolva újra illeszkedni fog az függvény grafikonjához. Emiatt a bal terület, ami integrálja t-től tu-ig, ugyanaz, mint 1 integrálja u-ig. Ez a második egyenlőséget geometriailag demonstrálja.

A hatványra vonatkozó összefüggés hasonlóan bizonyítható:
ahol a második egyenletben a változók helyettesítése: .
A természetes számok reciprokainak összege a harmonikus sor:
szorosan kapcsolódik a
különbséghez. Ha n tart a végtelenbe, akkor a különbség az Euler–Mascheroni-konstanshoz konvergál. Ez segít elemezni az algoritmusok bonyolultságát.[26]
A logaritmus egy másik integrál reprezentációja:
Ez azzal igazolható, hogy értéke megegyezik x = 1-ben, és ugyanaz a deriváltja.
Transzcendencia[szerkesztés]
Az egyváltozós valós függvényt algebrai függvénynek nevezzük, ha kielégíti a függvényegyenletet, ahol az egyes -ek az x változó polinomjai.[27] Azokat a valós függvényeket, amelyek nem algebraiak, transzcendens függvénynek nevezzük. Nevezetes tény, hogy a logaritmusfüggvény transzcendens.[28]
Kiszámítása[szerkesztés]
Bizonyos esetekben a logaritmus könnyen számítható, például lg 1000 = 3. Általában hatványsorok vagy a számtani-mértani közép felhasználásával számítják. Használhatók adott pontosságú táblázatok is a logaritmushoz.[29][30] A Newton-módszer szintén alkalmazható, mivel inverz függvénye, az exponenciális függvény gyorsan számítható.[31] Ha csak a bitenkénti eltolás és az összeadás érhető el alapműveletként, akkor keresőtáblák és CORDIC-szerű módszerek használhatók a logaritmus számítására. A bináris logaritmus algoritmus a kettes alapú logaritmust számolja sorozatos négyzetre emeléssel, ami ezt a kapcsolatot használja ki:
Hatványsorok[szerkesztés]

Minden 0 < z < 2 valós számra:[32]
Mivel ez a logaritmus Taylor-sora, ezért ez értelmezhető úgy is, hogy a
függvények egyre jobban megközelítik a természetes logaritmust. Például, ha z = 1,5, akkor a harmadik approximáció értéke 0,4167, ami 0,011-del nagyobb, mint ln(1,5) ~ 0,405465. A sorral a természetes logaritmus akármennyire megközelíthető, ha elég sok tagot összegezünk. Az elemi analízisben ln(z)-t tekintik a sor határértékének. Azonban a konvergencia nem érvényes mindenütt az értelmezési tartományban, ugyanis ez a sorozat a természetes logaritmus z = 1 körüli Taylor-sora, ami nem konvergálhat nagyobb sugarú körben, mert z = 0-ban a logaritmus nincs értelmezve. A Taylor-sor z = 1, |z| < 1-re nyújt közelítést:
Például a z = 0,1-re az első közelítés ln(1,1) ≈ 0,1, aminek hibája kevesebb, mint 5%, hiszen ln(1,1) ~ 0,0953.
Gyorsabban konvergáló sorok[szerkesztés]
Egy másik ismert sor az area hiperbolikus tangens függvényen alapul:
minden valós z > 0 számra.[32] A szigma jelöléssel
Ez a sor a Taylor-sorból származtatható, de gyorsabban konvergál annál, különösen, ha z közel van 1-hez. Ha z = 1,5, akkor az első három tag által a logaritmusra adott közelítés hibája megközelítően . A gyors konvergencia tovább gyorsítható: Legyen y ≈ ln(z) egy pontatlan közelítés. Legyen . Ekkor z logaritmusa: . Minél jobb a kezdeti y közelítés, annál közelebb lesz A 1-hez. Ez az A az exponenciális hatványsorral számítható, ami gyorsan konvergál, ha az adott y nem túl nagy. A nagyobb számok logaritmusa kisebb számok logaritmusának összegére bontható, például ha , akkor .
Az egészek logaritmusa egy rokon módszerrel számolható. A fenti sor alapján:
Ha az n szám logaritmusa ismert, akkor ez alapján számolható .
A számtani-mértani közepek módszere[szerkesztés]
A számtani-mértani közepek módszere egy viszonylag pontos közelítést ad a természetes logaritmusra. A következő képlet -et pontossággal (vagy p jegy pontossággal) közelíti (Carl Friedrich Gauss nyomán):[34][35]
ahol x és y számtani-mértani közepét jelöli. Ez úgy kapható, hogy először kiszámoljuk a pozitív x és y számok számtani és mértani közepét. Ezután ezt ismételgetjük a megkapott két számmal. Ezek gyorsan konvergálnak egy közös határértékhez, az számtani-mértani középhez. Az m szám a pontosságot biztosítja. Nagyobb m-ekhez az pontosabb értéke kell, de az eredmény is pontosabb. A π és az ln(2) konstansok más módszerekkel számolhatók.
Határértékek Hurwitz nyomán[szerkesztés]
A természetes logaritmusra teljesül:
ekvivalensen
amit a L’Hospital-szabály is megerősít.
Ezen alapulnak az Adolf Hurwitz által a illetve sorozatok a természetes logaritmussal definiált határértékei
ahol
Mivel és mert monoton csökken és monoton nő, azért mindkét sorozat konvergens. Mivel és , adódik az egyenlőség mindkét határértékre:
Azonban az kiszámítására a vészes kiegyszerűsödés (kivonáskor elvesző pontosság) miatt gyakorlatilag alkalmatlan.
Egyes bináris jegyek kiszámítása[szerkesztés]
Egy másik lehetőség a logaritmus kiszámítására, ha a számításokat kettes számrendszerben végezzük, és a jegyeket egymás után rendre számítjuk.[36] Ez az eljárás egyszerűen implementálható, mivel elkerüli az időigényes osztásokat, és könnyen alkalmazható a fixpontos aritmetikához is.
A kettes alapú logaritmus kiszámításához először leszámolják a kettes számrendszerbeli jegyeket, a számot 1 és 2 közé normálva. A művelet csak kettővel való osztásokat vagy szorzásokat igényel, ami binárisan nagyon gyors művelet. (Ezek számát meg kell jegyezni.)
Ha az adott szám x, akkor logaritmusa ábrázolható, mint:
amiből
Az x szám négyzetre emelése tehát egy jeggyel balra tolja a kettes logaritmust. A keletkező szám egészrésze a keresett logaritmusérték következő bináris jegye. Ez a jegy akkor 1, amikor x2 ≥ 2. Ha ez a feltétel teljesül, akkor x-et felezéssel újra normálják, ami nincs hatással a további jegyekre.[37]
Az algoritmus pszeudokódja:
INPUT 1 ≤ x < 2 OUTPUT A log2(x) törtrészének bi bitjei
i ← 0
LOOP
i ← i + 1
x ← x2 // A négyzetre emelés a logaritmusértéket megkettőzi.
IF x ≥ 2 THEN
x ← x / 2 // A felezést egy bites eltolással lehet megvalósítani.
bi ← 1 // bit 1
ELSE
bi ← 0 // bit 0
END IF
END LOOP
A kezdeti normálás során alkalmazott kettővel való szorzások számát utólag ki kell vonni a logaritmusértékből, vagy ha osztásokra volt szükség, hozzá kell ahhoz adni. (Mert egy szám kettővel való szorzása a logaritmusnál 1 hozzáadásával egyenértékű.)
(Az áttekinthetőség kedvéért a pszeudokód nem tartalmazza, de természetesen a ciklusból ki kell lépni; vagy adott pontosság elérésekor, vagy ami kézenfekvőbb, előre meghatározott számú logaritmusjegy létrehozásakor.)
Analóg számológép[szerkesztés]

A logaritmus analóg számológéppel is kiszámítható. Az eredmény az Ua feszültség, ami a bemeneti Ue feszültség logaritmusa. Ez a dióda áram-feszültség exponenciális karakterisztikáját használja ki. A mellékelt ábra a logaritmáló elvi felépítését mutatja be, egy D diódával és egy R ellenállással.[38]
Negatív és komplex számok logaritmusa[szerkesztés]



A logaritmus általánosítható minden, nullától különböző komplex számra, így a negatív számokra is. Adott z komplex szám természetes logaritmusa az a komplex szám, ha A más alapú logaritmusok ebből számíthatók. Ez azonban nem egyértelmű.[33]
Nézzük meg egy komplex szám logaritmusát: ahol a valós szám, a komplex szám abszolútértéke, mely a képlettel számítható ki, és pedig a és a valós tengely pozitív része által bezárt szög (radiánban). Az argumentum nem egyértelmű; ha argumentuma a komplex számnak, akkor és is argumentuma z-nek, ugyanis a 2π hozzáadása vagy kivonása a komplex számsík egy 360 fokos forgatásnak felel meg, ami minden komplex számot önmagára képez. Az argumentum főértéke az a φ, amire . Jelölése .[39] (Egyes szerzők ehelyett a megkötést használják.[40])
A komplex szinusz és koszinusz, vagy a komplex exponenciális függvény felhasználásával r-re és φ-re rendre a következők teljesülnek:[41]
ahol a valós természetes logaritmus, a komplex logaritmusa, és tetszőleges egész.
Innen következik, hogy e a-adik hatványa z, ha
ahol φ a z argumentumának főértéke, és k tetszőleges egész. Minden ilyen a érték logaritmusa z-nek. Ezekből végtelen sok van, szemben az egyértelmű valós logaritmussal. A logaritmus egyenletei erre a végtelen értékű logaritmusra megmaradnak. Az -val definiált érték a logaritmus főértéke, . A pozitív számok argumentumának főértéke 0, így a komplex logaritmus főértéke valós szám, és megegyezik a valós logaritmussal. A főértékre szorítkozva azonban elvesznek az azonosságok, mert az egyenlőség lehet, hogy a logaritmus egy másik értékét választva teljesülne.[42]
A jobbra lent látható kép a természetes logaritmus főágát mutatja be. A negatív oldalon a szín az argumentum ugrása miatt változik meg hirtelen. Ez csak azzal kerülhető el, hogy az argumentum nagyságára nem teszünk kikötést, de ekkor visszakapjuk a végtelen értékű logaritmust. Habár a negatív számok logaritmusa is értelmezett a komplex számsíkon, a negatív számok logaritmusának nincs főértéke.[43]
- Egy komplex szám alapú logaritmust pedig kiszámíthatunk az előbbi összefüggések alapján: , ahol és komplex szám.[44]
- Negatív számok logaritmusa kiszámítható az előző összefüggésekkel, ugyanis minden valós szám egyben komplex szám is.
Más exponenciális függvények inverzei[szerkesztés]
A matematikában több részterületen is használják a hatványozást, így az inverz függvények is szóba kerülnek. Például a mátrixok hatványozásának egyik inverz függvénye a többértékű mátrixlogaritmus.[45] Egy másik példa a p-adikus számokon értelmezett p-adikus logaritmus, ami a p-adikus exponenciális inverze. Mindezeket a valós Taylor-sor alapján definiálják.[46] A differenciálgeometriában egy exponenciális leképezés egy sokaság egy pontjabeli érintőteret a pont környezetére képezi. Ennek inverzét szintén logaritmikus leképezésnek nevezik.[47]
A véges csoportok körében egy elem hatványa az elem önmagával való szorzásával kapható meg. Mivel véges csoportban az elemek rendje véges, negatív kitevőkre nincs szükség, mivel az elemek inverze is előáll pozitív kitevős hatványként.[48] Az x csoportelem b csoportelem alapú diszkrét logaritmusa az az egész n szám, ami megoldja az
egyenletet. Jelen ismereteink szerint míg a hatványozás véges csoportokban gyorsan elvégezhető, addig a diszkrét logaritmus bizonyos csoportokban nehezen számítható.[48] Ezt az aszimmetriát kihasználják a nyilvános kulcsú titkosírásban, például a Diffie–Hellman-kulcscsere eljárásban, ami lehetővé teszi a titkosírás kulcsának cseréjét nyilvános csatornán.[49] A Zech-féle logaritmus véges testek multiplikatív csoportján értelmezett diszkrét logaritmus.[50]
A további logaritmusszerű inverz függvények közé tartoznak az iterált logaritmus, a ln(ln(x)) kettős logaritmus, ami a kettős exponenciális inverze; a hiper- vagy szuperlogaritmus, ami a tetráció inverze; a Lambert-féle W-függvény, ami a f(w) = wew inverze;[51] és a logit, ami a logisztikus függvény inverze.[52]
Kapcsolódó fogalmak[szerkesztés]
Absztrakt algebrai szempontból a egyenlőség csoportizomorfia a pozitív valós számok szorzásra vett csoportja és a valós számok additív csoportja között. E között a két csoport között csak a logaritmusfüggvények teremtenek csoportizomorfiát.[53] Ezzel az izomorfiával a Haar-mérték, Lebesgue-mérték a valós számokon megfelel a dx/x mértéknek a pozitív valós számokon.[54]
A komplex analízisben és az algebrai geometriában a df/f alakú differenciálformák logaritmikus pólusokként ismertek.[55]
A polilogaritmus definíciója:
A természetes logaritmussal kifejezve: Li1(z) = −ln(1 − z), továbbá Lis(1) éppen a ζ(s) Riemann-féle zéta-függvény.[56]
Alkalmazások[szerkesztés]


A logaritmusnak számos alkalmazása van a matematikában és azon kívül. Ezek jelentős része a skálainvarianciát használja fel. Például a nautilus héjának minden egyes kamrája olyan, mint az előző, de egy konstans tényezővel nagyobb. Emiatt a héj keresztmetszete logaritmikus spirál.[57] Benford törvénye is a skálainvarianciára hivatkozik.[58] A logaritmus az önhasonlósághoz is kapcsolódik, emiatt jelenik meg az oszd meg és uralkodj típusú algoritmusok műveletigényében[59] önhasonló geometriai alakzatok fraktáldimenziójának is logaritmus használatával számítható ki. A logaritmikus skálák akkor hasznosak, ha vagy különböző nagyságrendű mennyiségeket kell egy skálán ábrázolni, vagy az abszolút különbség helyett a relatív megváltozást kell megjeleníteni. A logaritmus több tudományos képletnek is része, mint a Ciolkovszkij-egyenlet, a Fenske-egyenlet és a Nernst-egyenlet.
Számítások[szerkesztés]
A fenti tulajdonságok segítségével, ha minden szám logaritmusát tudjuk, akkor a szorzások csupán összeadás műveletével elvégezhetőek, sőt, a hatványozást először szorzásra visszavezetve szintén két összeadással elvégezhetjük. A kitevők összeadását a logaritmus értékeket skálájában tartalmazó logarléc használatakor egyszerű tologatással megoldhatjuk.[60] A logarlécet napjainkban már nemigen használják, de az elv továbbra is használható például számológépekben.
Mivel a logaritmus additívvá teszi az egymással szorzódó mennyiségeket, mint például állapotok valószínűségét, alapvető szerepet játszik a statisztikus fizikában használatos entrópia, illetve azzal gazdag analógiákat mutató információmennyiség, hírérték megadásában.
Bonyolultság[szerkesztés]
A bonyolultságelmélet a számítástudománynak az az ága, amely az algoritmusok végrehajtásának idejét vizsgálja.[61] A logaritmusok azoknak a feladatoknak a vizsgálatában jelennek meg, amelyeket úgy oldanak meg, hogy részproblémákra osztják, azokat megoldják, majd ezekből állítják elő a feladat megoldására. Erre a módszerre oszd meg és uralkodj módszerként is utalnak.[62]
Például a logaritmikus keresés egy rendezett listában keres egy elemet. Ehhez a középső elemet vizsgálja meg. Ha ez kisebb, akkor a nagyobb, ha nagyobb, mint a keresett elem, akkor a kisebb elemek között keres tovább ugyanígy. Ha az adott elem megegyezik a vizsgált elemmel, akkor megvan a keresett elem. Ha a lista már nem osztható tovább, és nem találta meg a keresett elemet, akkor a keresett elem nincs a listában. Az esetek legalább felében ez összesen összehasonlítást jelent.[63] Hasonlóan az összefuttatásos rendezés megfelezi a kapott listát, rendezi a két részt, majd összefuttatva kapja meg a teljes lista rendezését. Az egy elemű listák rendezettje önmaguk. Ez összesen .[64] A bonyolultságelméletben rendszerint nem határozzák meg a logaritmus alapját, mert az egy konstans szorzót jelent, és ettől a bonyolultságelmélet eltekint.[65]
Ha f(x) függvény, akkor logaritmikusan nő, ha egy logaritmusfüggvény konstansszorosa. Ez azt is jelenti, hogy logaritmusfüggvény. Például egy természetes szám leírásához egy rögzített számrendszerben szükséges jegyek száma logaritmikusan nő a számhoz képest. Más szavakkal, az eltárolásához szükséges memória logaritmikusan nő a számmal. A biológiában azonban az exponenciális növekedést nevezik logaritmikusnak.[66]
Entrópia és káosz[szerkesztés]

Az entrópia egy adott rendszer rendezettségét méri. A statisztikai termodinamikában
az információk elméletében
Az összeg az összes i állapotot, illetve elemet magába foglalja. Itt pi az adott állapot vagy elem valószínűsége, k a Boltzmann-állandó. Az információelméletben az információ mennyiségét méri. Ha N üzenet mindegyike egyforma valószínűségű, akkor a kiválasztott üzenet információtartalma log2(N) bit.[67]
A Ljapunov-kitevők dinamikus rendszerek kaotikusságát méri a logaritmussal. Például, ha egy részecske egy ovális biliárdasztalon mozog, akkor a kiindulópont kis mértékű megváltoztatása is a részecske útjának nagy mértékű változását eredményezi. Az ilyen rendszerek determinisztikusan kaotikusak, mivel megjósolható, hogy kis mérési hibák is nagy különbséget eredményeznek a végső állapotban.[68] A determinisztikusan kaotikus rendszerekben legalább egy Ljapunov-kitevő pozitív.
Fraktálok[szerkesztés]

A logaritmus megjelenik a fraktáldimenziók definíciójában.[69] A fraktálok önhasonló geometriai alakzatok, ami azt jelenti, hogy (legalább köznapi vagy statisztikai értelemben) hasonlók önmaguk egy részével. Például a Sierpiński-háromszög lefedhető három önmaga felére kicsinyített másolatával, így Hausdorff-dimenziója log(3)/log(2) ≈ 1,58. Egy másik logaritmuson alapuló definíció a dobozszámlálási dimenzió, ami különböző méretű dobozokkal való fedésből indul ki.
Valószínűségszámítás és statisztika[szerkesztés]


A valószínűségszámításban is megjelenik a logaritmus. A nagy számok törvénye szerint egy szabályos érmével nagyon sokszor dobva a fejek aránya megközelíti az 1/2-et. A tétel nem állít semmit sem a fej és az írás különbségéről, az a végtelenbe tartva végtelenre nőhet. Az 1/2-es arány körüli ingadozásokat az iterált logaritmus törvénye írja le.[70]
A logaritmus a lognormál eloszlásra is jellemző. Ha egy mennyiség eloszlása normális, akkor logaritmusának eloszlása lognormális.[71] A lognormális eloszlás gyakori, és hátterében sok pozitív értékű, összeszorzódó valószínűségi változó áll. Erre egy példa a turbulencia tanulmányozása.[72]
A paraméteres statisztikai modellek egyike a maximum-likelihood becslés. Ebben a modellben a likelihood függvény legalább egy olyan paramétertől függ, amit becsülni kell. Ez a függvény ott maximális, ahol logaritmusa maximális, mivel a logaritmus monoton nő. Ennek egyszerűbb megtalálni a maximumát, különösen akkor, ha a likelihood függvény független valószínűségi változók több tényezős szorzata.[73]
Benford törvénye a számjegyek eloszlását írja le különféle adathalmazokban, például épületek magassága. Eszerint annak a valószínűsége, hogy egy számadat első jegye d, megegyezik a mennyiséggel, függetlenül a mértékegységtől.[74] Így az adatok 30%-a 1-gyel, 18%-a 2-vel kezdődik, és így tovább. Ezt a szabályszerűséget használják például könyvelési csalások leleplezésére.[75]
Számelmélet[szerkesztés]
A természetes logaritmus kapcsolódik a prímszámok (2, 3, 5, 7, 11 stb.) eloszlásához, ami a számelmélet egy régi nevezetes problémája. Minden x egész számhoz rendeljük hozzá a nála nem nagyobb pozitív prímek számát; ezt a függvényt π(x) jelöli. Ennek aszimptotikus közelítése a prímszámtétel szerint:
ami azt jelenti, hogy a két függvény hányadosa tart az egyhez, ha x tart a végtelenbe.[76] Eszerint annak a valószínűsége, hogy egy x-nél nem nagyobb véletlen szám prím, közelítőleg fordítottan arányos x számjegyeinek számával.
Egy jobb közelítés:
A Riemann-hipotézis megfogalmazható π(x) and Li(x) összehasonlításával.[77] A számok prímtényezőiről szóló Erdős–Kac-tételben szintén megjelenik a logaritmus.
Az n faktoriálisának logaritmusa () kifejezhető, mint
Ebből levezethető a Stirling-formula, ami n! approximációja.[78]
Logaritmikus skálák[szerkesztés]
A logaritmus használatával mennyiségek sok nagyságrendjét egy skálára sűríthetjük. Ennek hasznosságát gyakran a gyakorlat és természet törvényszerűségei is alátámasztják. A különböző fizikai mennyiségék (hangerősség, hangmagasság, fényintenzitás stb.) által keltett, általunk érzékelt fiziológiai érzet a fizikai jel (teljesítményének) logaritmusával arányos. Ez indokolja a logaritmussal arányos decibel-skálák bevezetését. A decibel a teljesítmény 10-es alapú logaritmusának 10-szerese, vagy az elektromos feszültség 10-es alapú logaritmusának 20-szorosa. Használják az elektromos jelek szállítása közbeni feszültségesés mérésére,[79] a hangok teljesítményének mérésére az akusztikában,[80] vagy a fény elnyelődésének mérésére az optikában és a spektrometriában. A jel-zaj arányt is decibelben mérik.[81] A csúcs jel-zaj arányt használják a képtömörítés és a hangminőség mérésére.[82]
Az érzékelés leírásában gyakran jelenik meg a logaritmus.[83][84] A hangmagasság érzete a hang frekvenciájának logaritmusával arányos, azaz például egyenletes léptéknek észlelt oktávok rendre a frekvencia 2-, 4-, 8-szorosát jelentik. A csillagok fényességét mérő magnitudó is logaritmikus.[85] A pszichofizikában a Weber–Fechner-törvény szerint az inger és az érzet erőssége között logaritmikus kapcsolat van.[86] Ez azonban kevésbé pontos, mint egyes ma használt összefüggések, mint például Steven törvénye.[87]
Hick törvénye szerint a választási idő arányos az alternatívák számának logaritmusával.[88] Fitt törvénye szerint egy tárgy méretének és távolságának logaritmusa arányos az odasietés idejével.[89] A matematikában képzetlen embereknél tendencia, hogy a mennyiségeket logaritmusuk szerint becsülik meg, például a 10 az 1 és a 100 között félúton van. Az alaposabb matematikai képzés ezt bizonyos körülmények esetén lineáris irányba tolja el.[90][91]
Logaritmikus továbbá a földrengés erősségét jelző Richter-skála is; a földrengés által kibocsátott energia 10 alapú logaritmusa. Például, ha egy földrengés erőssége 5,0, akkor 32-szer (101,5) akkora; a 6,0 erősségű 1000-szer (103) akkora, mint egy 4,0 erejű földrengés.[92]
Egy további példa a vizes oldatok pH-ja, ami a oxóniumionok koncentrációjának 10-es alapú logaritmusának ellentettje.[93] Például a semleges pH-jú vízben ez a koncentráció 10−7 mol·L−1, ami szerint a pH 7. Az ecet pH-ja 3. A különbség az oldatban levő oxóniumionok koncentrációjának 10000-szeresét jelzi; eszerint az ecetben 10−3 mol·L−1 oxóniumion található.
Zene[szerkesztés]


A hangmagasság logaritmikus észleléséhez a zenének is alkalmazkodnia kell. Az egyenletes hangolásban az egyes hangközök mérete csak a két hang távolságától függ, és nem maguktól a hangoktól. Például az a' (440 Hz) és a b' hangok (466 Hz) közötti hangköz ugyanakkora, mint a b (466 Hz) és a h (493 Hz) hangok közötti. Eszerint a frekvenciák közötti arányok megegyeznek, vagy csak annyiban térnek el, amennyiben a fül nem érzékeli a különbséget:
A hangközöket az elnevezések mellett (például nagy szekund, kis terc, tiszta kvint) logaritmikusan célszerű mérni. A logaritmus alapja 21/12, ami az oktáv frekvenciaarányához és az oktáv által tartalmazott 12 hanghoz alkalmazkodva ez a legkisebb nem prím hangköz, a kis szekund frekvenciaaránya. Ez a száz cent. A centet a nem egyenletesen temperált hangolások beállításához használják.[94]
| Hangköz (két egyszerre játszott hang között) |
1/12 egész hang |
Kis szekund |
Akusztikus nagy terc[95] |
Nagy terc |
Tritónusz |
Oktáv |
| Frekvenciaarány r | ||||||
| Kis szekundokban (félhangokban) |
||||||
| Centekben |
Grafikonok[szerkesztés]

A szemilog grafikonok a logaritmikus skálát is szemléltetik. Az egyik tengelyen, tipikusan a függőlegesen a skála logaritmikus, Például az itt látható grafikon több nagyságrendet összenyomva mutatja be a német hiperinflációt az 1920-as években. Ezeken a grafikonokon az alakú exponenciális függvények képe egyenes.
A természetben talált legtöbb összefüggés (például fizikai képlet) hatványfüggvény alakú. Ha mindkét tengelyen szereplő értékeknek logaritmusát ábrázoljuk, az ún. log-log ábrán bármely hatványfüggvény lineáris alakot vesz fel, a meredekség pedig a kitevőt adja meg:
A fenti elvet használják ki a gyakran alkalmazott különböző logaritmikus grafikonokon, például a Bode-diagram, amely egy rendszer átviteli függvényének log-log ábrázolása.[96]

Története[szerkesztés]
Előzmények[szerkesztés]
A babilóniak Kr. e. 2000–1600 körül kezdték el alkalmazni a negyednégyzet algoritmust szorzásra, ami csak összeadást, kivonást és egy, négyzetek negyedét tartalmazó táblázatot használt.[97][98] A módszer alkalmazásához ki kell számítani a tényezők összegét és különbségét, és az összeg négyzetének negyedéből kivonni a különbség négyzetének negyedét. Mivel adott két egész szám összege és különbsége egyszerre páros és páratlan, a táblázatban az egyszerűség kedvéért elhagyták a páratlan négyzetekből adódó negyedeket, azaz minden négyzet negyedének vették az egészrészét. Azonban ez még nem volt alkalmas osztásra, mert ahhoz még a reciprokok táblázatára is szükség lett volna, vagy egy olyan eljárásra, amivel gyorsan lehetett volna reciprokot számolni. A módszert az újkorban újra felfedezték, és 1817-től kezdve egészen a számológépek elterjedéséig kiadtak negyednégyzeteket tartalmazó táblázatokat nagy számok pontos szorzásához.
Az indiai Virasena azzal foglalkozott, hogy hányszor lehet elfelezni egy páros számot. 2 egész kitevős hatványaira ez a logaritmus. Ezt ardhacchedának nevezte. Továbbá foglalkozott hasonló függvényekkel 3 és 4 alapra (trakacheda és caturthacheda).[99] Ma ezt a p-adikus számok kapcsán a számok rendjének nevezzük.
Michael Stifel 1544-ben Nürnbergben kiadott Arithmetica integrája tartalmazott egy táblázatot[100] az egészekről és 2 hatványairól, ami egy korai logaritmustáblának tekinthető.[101][102]
A 16. és a 17. században közelítő pontosságú szorzásra és osztásra a prosthaphaeresis algoritmust használták, ami a
képleten alapulva összeadásra, kivonásra és táblázatok használatára egyszerűsítette a műveleteket. A logaritmus azonban még ezt is tovább egyszerűsítette. Az Euler-formulával kimutatható az összefüggés a két képlet között.
Napiertől Eulerig[szerkesztés]

A logaritmusok módszerét John Napier 1614-ben jelentette meg Mirifici Logarithmorum Canonis Descriptio címen.[103][104] Jobst Bürgi (avagy Joost Bürgi, Justus Byrgius) logaritmustáblája 1620-ban jelent meg, de nem terjedt el széles körben. Ez egy egyhez közeli számot használt alapnak, és az 1-től 10-ig terjedő számok logaritmusát tartalmazta. Napiertől eltérően nem definiálta a folytonos logaritmusfüggvényt, és nem elemezte az interpolációk pontosságát sem. Még a használat szabályait sem írta le, bár ezt a hiányosságát később pótolta. Ezt külön adták ki.[105][106]
Johannes Kepler az Ephemeris fordításához logaritmustáblákat használt, ezért művét Napiernek ajánlotta.[107] Napier rendszerének megjelenését ugyan megelőzte Jobst Bürgi, ám ő ahelyett, hogy a köz szeme előtt nevelte volna fel gyermekét, már születése után magára hagyta.[108]
Napier ismételt kivonásokkal kiszámolta (1 − 10−7)L értékét minden egész L-re 1-től 100-ig, ahol is megközelítően 0,99999 = 1 − 10−5-t ért el. Ezután kiszámolta ezeknek a szorzatait 107(1 − 10−5)L-nel 1-től 50-ig, és hasonlókat számolt 0,9998 ≈ (1 − 10−5)20-nal és |0,9 ≈ 0,99520-nal is. Mindezek a számítások 20 évig tartottak, és lehetővé tették, hogy 5 és 10 millió között minden N-hez megadja azt az L számot, ami megoldja az
egyenletet. Az L számot először mesterséges számnak nevezte, de később a logaritmus nevet adta neki, mivel a szám arányt jelöl. Napier kapcsolata a természetes logaritmussal:[109]
ami egy nagyon pontos approximáció, és megfelel az
megfigyelésnek. A logaritmus hamarosan találkozott az igényekkel, és gyorsan népszerűvé vált. Bonaventura Cavalieri (Itália), Edmund Wingate (Franciaország), Xue Fengzuo (Kína) művei, és a német Johannes Kepler Chilias logarithmorum című műve segítette az elterjedésben.[110]
1649-ben Alphonse Antonio de Sarasa, aki korábban Grégoire de Saint-Vincent tanítványa volt, kapcsolatba hozta a logaritmust a hiperbola kvadratúrájával.[111] Rámutatott arra, hogy a hiperbola alatti f(t) terület x = 1-től x = t-ig eleget tesz a következőnek:
Ennek előzményeként Grégoire de Saint-Vincent 1647-ben megjelent könyvében, az Opus geometricum quadraturae circuli et sectionum coni vizsgálta a kúpszeleteket.[112] Ebben bizonyította, ha a pontok abszcisszái mértani arányban állnak, akkor a hiperbola íve és az abszcisszák által meghatározott görbe alatti terület számtani arányban van. Ezt felhasználva látta be Alphonse Antonio de Sarasa a fenti összefüggést, és a kapcsolatot a logaritmussal.[111]
A természetes logaritmust Nicholas Mercator 1668-ban kiadott könyvében, a Logarithmotechniában vezette be,[113] habár John Speidell matematikatanár Napier nyomán már készített természetes logaritmus táblázatot.[114] 1730-ban Euler definiálta a természetes alapú exponenciális függvényt és logaritmust,
és megmutatta, hogy e kettő inverze egymásnak.[115][116][117]
Történelmi alkalmazások[szerkesztés]

A számítások leegyszerűsítésével a logaritmus hozzájárult a természettudományok, különösen a csillagászat fejlődéséhez. Kritikus fontosságú volt a geodéziában, az égi navigációhoz, és sok más területhez. Pierre-Simon Laplace szerint a több hónapos számításokat néhány naposra rövidíti, és a hibákat is csökkenti.[118]
A számológépek megjelenése előtt a logaritmust táblázatok alapján használták.[119] Az első ilyen táblázatot Napier után nem sokkal Henry Briggs készítette 1617-ben. Ezután egyre pontosabb és egyre nagyobb számtartományokra készültek logaritmustáblázatok. Ezek a táblázatok tartalmazták és értékét, ahol az x szám egy bizonyos lépésközzel befutott egy tartományt, és b legtöbbször 10 volt a 10-es számrendszerhez való alkalmazkodás miatt. Briggs táblázata az 1–1000 egészek logaritmusát tartalmazta 8 jegyes pontossággal. A inverz függvényét, -et antilogaritmusnak nevezték.[120] A logaritmus alapvető tulajdonságai alapján a szorzást összeadásra, az osztást kivonásra, a hatványozást szorzásra, és a gyökvonást osztásra vezették vissza. Ezután az így kapott érték antilogaritmusát keresték vissza ugyanabban a táblában.
Így a c és a d számok szorzata
és hányadosa
A 10-es alapú logaritmus nullákat számláló tulajdonságára támaszkodva egyes táblák külön adták meg a karakterisztikát (a logaritmus egészrészét) és a mantisszát (a logaritmus törtrészét).[121] A tízes alapú logaritmusának karakterisztikája 1-gyel nagyobb, mint x karakterisztikája, így a 10-es alapú logaritmustábla értelmezési tartománya kibővíthető. Így például, ha adva vannak az 1-től 1000-ig terjedő egész számok 10-es alapú logaritmusai, 3542 logaritmusa közelíthető így:
Egy másik alkalmazás a logarléc volt, amiben két logaritmikus skálát használtak a számításokhoz.

Az első logarlécet 1620–1630 körül az oxfordi Edmund Gunter készítette, és csak egy logaritmikus skálája volt. További mérőeszközökkel kombinálva szorozni és osztani lehetett vele. 1632-ben a cambridge-i William Oughtred két Gunter-vonalzó összetételével megalkotta a modern logarlécet. Ezeken a skálákon a számok logaritmusuk különbségével arányos távolságra kerültek. A felső skála elcsúsztatásával lehetett összeadni a logaritmusokat. Például a felső skálán az 1 és a 2 közötti távolságot az alsó skálán 1-től 3-ig terjedő távolsághoz adva a szorzat az alsó skáláról olvasható le. Az elektronikus számológépek elterjedéséig (1970-es évek) használták még mérnökök és kutatók is, mert a pontosság árán fel lehetett gyorsítani a számításokat.[115]
Jegyzetek[szerkesztés]
- ↑ Neukirch, Jürgen. Algebraic Number Theory, Grundlehren der mathematischen Wissenschaften. Berlin: Springer-Verlag (1999). ISBN 978-3-540-65399-8
- ↑ University, IFS, Massey: Inverse Operations, Maths First, Institute of Fundamental Sciences, Massey University. mathsfirst.massey.ac.nz. (Hozzáférés: 2017. augusztus 5.)
- ↑ Logarithmus. www.mathematik-wissen.de. (Hozzáférés: 2017. augusztus 5.)
- ↑ Hasonló, de nem tízes, hanem természetes logaritmus felhasználásával definiált mértékegység a neper.
- ↑ a b c d e Hajnal Imre: Matematika III.
- ↑ Kate, S.K. & Bhapkar, H.R. (2009), Basics Of Mathematics, Pune: Technical Publications, ISBN 978-81-8431-755-8, <https://books.google.com/books?id=v4R0GSJtEQ4C&pg=PR1#v=onepage&q&f=false>, chapter 1
- ↑ Lásd például Hajnal Imre: Matematika III.
- ↑ Downing, Douglas (2003), Algebra the Easy Way, Barron's Educational Series, Hauppauge, N.Y.: Barron's, ISBN 978-0-7641-1972-9, chapter 17, p. 275
- ↑ Wegener, Ingo (2005), Complexity theory: exploring the limits of efficient algorithms, Berlin, New York: Springer-Verlag, ISBN 978-3-540-21045-0, p. 20
- ↑ a b Van der Lubbe, Jan C. A. (1997), Information Theory, Cambridge University Press, p. 3, ISBN 9780521467605, <https://books.google.com/books?id=tBuI_6MQTcwC&pg=PA3>.
- ↑ Allen, Elizabeth & Triantaphillidou, Sophie (2011), The Manual of Photography, Taylor & Francis, p. 228, ISBN 9780240520377, <https://books.google.com/books?id=IfWivY3mIgAC&pg=PA228>.
- ↑ Obádovics J. Gyula: Matematika
- ↑ Archivált másolat. [2015. június 20-i dátummal az eredetiből archiválva]. (Hozzáférés: 2015. június 20.)
- ↑ Archivált másolat. [2015. május 20-i dátummal az eredetiből archiválva]. (Hozzáférés: 2015. június 20.)
- ↑ a b Lang, Serge (1997), Undergraduate analysis (2nd ed.), Undergraduate Texts in Mathematics, Berlin, New York: Springer-Verlag, ISBN 978-0-387-94841-6, section III.3
- ↑ a b Lang 1997, section IV.2
- ↑ a b c Archivált másolat. [2015. június 20-i dátummal az eredetiből archiválva]. (Hozzáférés: 2015. június 20.)
- ↑ Dieudonné, Jean. Foundations of Modern Analysis. Academic Press, 84. o. (1969) item (4.3.1)
- ↑ Stewart, James (2007), Single Variable Calculus: Early Transcendentals, Belmont: Thomson Brooks/Cole, ISBN 978-0-495-01169-9, section 1.6
- ↑ Calculation of 'd/dx(Log(b,x))'. Wolfram Alpha. Wolfram Research. [2011. július 18-i dátummal az eredetiből archiválva]. (Hozzáférés: 2011. március 15.)
- ↑ Bárczi Barnabás: Differenciálszámítás
- ↑ Kline, Morris (1998), Calculus: an intuitive and physical approach, Dover books on mathematics, New York: Dover Publications, ISBN 978-0-486-40453-0, p. 386
- ↑ Calculation of 'Integrate(ln(x))'. Wolfram Alpha. Wolfram Research. [2011. július 18-i dátummal az eredetiből archiválva]. (Hozzáférés: 2011. március 15.)
- ↑ Abramowitz & Stegun, eds. 1972, p. 69
- ↑ Courant, Richard (1988), Differential and integral calculus. Vol. I, Wiley Classics Library, New York: John Wiley & Sons, ISBN 978-0-471-60842-4, section III.6
- ↑ Havil, Julian (2003), Gamma: Exploring Euler's Constant, Princeton University Press, ISBN 978-0-691-09983-5, sections 11.5 and 13.8
- ↑ Transcendental Functions. www.phengkimving.com. (Hozzáférés: 2017. augusztus 10.)
- ↑ Transcendency. www.phengkimving.com. (Hozzáférés: 2017. augusztus 10.)
- ↑ Muller, Jean-Michel (2006), Elementary functions (2nd ed.), Boston, MA: Birkhäuser Boston, ISBN 978-0-8176-4372-0, sections 4.2.2 (p. 72) and 5.5.2 (p. 95)
- ↑ Hart, Cheney, Lawson et al. (1968), Computer Approximations, SIAM Series in Applied Mathematics, New York: John Wiley, section 6.3, p. 105–111
- ↑ Zhang, M.; Delgado-Frias, J.G. & Vassiliadis, S. (1994), "Table driven Newton scheme for high precision logarithm generation", IEE Proceedings Computers & Digital Techniques 141 (5): 281–292, ISSN 1350-2387, doi:10.1049/ip-cdt:19941268, <http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=326783>, section 1 for an overview
- ↑ a b Abramowitz & Stegun, eds. 1972, p. 68
- ↑ a b Halász Gábor: Komplex függvénytan
- ↑ Sasaki, T. & Kanada, Y. (1982), "Practically fast multiple-precision evaluation of log(x)", Journal of Information Processing 5 (4): 247–250, <http://ci.nii.ac.jp/naid/110002673332>. Hozzáférés ideje: 30 March 2011
- ↑ Ahrendt, Timm (1999), Fast computations of the exponential function, vol. 1564, Lecture notes in computer science, Berlin, New York: Springer, pp. 302–312, DOI 10.1007/3-540-49116-3_28
- ↑ Thomas Preußer: Pearls of Computer Arithmetic: The Binary Logarithm. www.linkedin.com (2017. január 31.) (Hozzáférés: 2018. június 6.)
- ↑ http://www.claysturner.com/dsp/BinaryLogarithm.pdf
- ↑ Archivált másolat. [2015. június 23-i dátummal az eredetiből archiválva]. (Hozzáférés: 2015. június 23.)
- ↑ Ganguly, S. (2005), Elements of Complex Analysis, Kolkata: Academic Publishers, ISBN 978-81-87504-86-3, Definition 1.6.3
- ↑ Nevanlinna, Rolf Herman & Paatero, Veikko (2007), "Introduction to complex analysis", London: Hilger (Providence, RI: AMS Bookstore), ISBN 978-0-8218-4399-4, section 5.9
- ↑ Moore, Theral Orvis & Hadlock, Edwin H. (1991), Complex analysis, Singapore: World Scientific, ISBN 978-981-02-0246-0, section 1.2
- ↑ Ivan Francis Wilde: Lecture Notes on Complex Analysis. London: Imperial Collage Press. 2006. 99. o. ISBN 978-1-86094-642-4 Hozzáférés: 2018. június 1. 6.1. tétel
- ↑ Halász Gábor: komplex függvénytan
- ↑ http://www.maa.org/sites/default/files/269138324871.pdf
- ↑ Higham, Nicholas (2008), Functions of Matrices. Theory and Computation, Philadelphia, PA: SIAM, ISBN 978-0-89871-646-7, chapter 11.
- ↑ Neukirch, Jürgen. Algebraic Number Theory, Grundlehren der mathematischen Wissenschaften. Berlin: Springer-Verlag (1999). ISBN 978-3-540-65399-8
- ↑ Hancock, Edwin R.; Martin, Ralph R. & Sabin, Malcolm A. (2009), Mathematics of Surfaces XIII: 13th IMA International Conference York, UK, September 7–9, 2009 Proceedings, Springer, p. 379, ISBN 978-3-642-03595-1, <https://books.google.com/books?id=0cqCy9x7V_QC&pg=PA379>
- ↑ a b Diszkréció diszkrét logaritmussal. [2015. június 21-i dátummal az eredetiből archiválva]. (Hozzáférés: 2015. június 21.)
- ↑ Stinson, Douglas Robert (2006), Cryptography: Theory and Practice (3rd ed.), London: CRC Press, ISBN 978-1-58488-508-5
- ↑ Lidl, Rudolf & Niederreiter, Harald (1997), Finite fields, Cambridge University Press, ISBN 978-0-521-39231-0
- ↑ Corless, R.; Gonnet, G. & Hare, D. et al. (1996), "On the Lambert W function", Advances in Computational Mathematics (Berlin, New York: Springer-Verlag) 5: 329–359, ISSN 1019-7168, doi:10.1007/BF02124750, <http://www.apmaths.uwo.ca/~djeffrey/Offprints/W-adv-cm.pdf>. Hozzáférés ideje: 2015-05-29
- ↑ Cherkassky, Vladimir; Cherkassky, Vladimir S. & Mulier, Filip (2007), Learning from data: concepts, theory, and methods, Wiley series on adaptive and learning systems for signal processing, communications, and control, New York: John Wiley & Sons, ISBN 978-0-471-68182-3, p. 357
- ↑ Bourbaki, Nicolas (1998), General topology. Chapters 5—10, Elements of Mathematics, Berlin, New York: Springer-Verlag, ISBN 978-3-540-64563-4, section V.4.1
- ↑ Ambartzumian, R. V. (1990), Factorization calculus and geometric probability, Cambridge University Press, ISBN 978-0-521-34535-4, section 1.4
- ↑ Esnault, Hélène & Viehweg, Eckart (1992), Lectures on vanishing theorems, vol. 20, DMV Seminar, Basel, Boston: Birkhäuser Verlag, ISBN 978-3-7643-2822-1, section 2
- ↑ Apostol, T.M..szerk.: Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W.: Logarithm, NIST Handbook of Mathematical Functions. Cambridge University Press. 25.12 (2001). ISBN 978-0521192255
- ↑ Maor 2009, p. 135
- ↑ Frey, Bruce (2006), Statistics hacks, Hacks Series, Sebastopol, CA: O'Reilly, ISBN 978-0-596-10164-0, <https://books.google.com/?id=HOPyiNb9UqwC&pg=PA275&dq=statistics+hacks+benfords+law#v=onepage&q&f=false>, chapter 6, section 64
- ↑ Ricciardi, Luigi M. (1990), Lectures in applied mathematics and informatics, Manchester: Manchester University Press, ISBN 978-0-7190-2671-3, <https://books.google.de/books?id=Cw4NAQAAIAAJ>, p. 21, section 1.3.2
- ↑ Roger R. Flynn. Computer sciences. Macmillan, 175. o. (2002. június 1.). ISBN 978-0-02-865567-3. Hozzáférés ideje: 2013. március 30. „The slide rule is an example of a mechanical analog computer...”
- ↑ Wegener, Ingo (2005), Complexity theory: exploring the limits of efficient algorithms, Berlin, New York: Springer-Verlag, ISBN 978-3-540-21045-0, pages 1-2
- ↑ Harel, David & Feldman, Yishai A. (2004), Algorithmics: the spirit of computing, New York: Addison-Wesley, ISBN 978-0-321-11784-7, p. 143
- ↑ Knuth, Donald (1998), The Art of Computer Programming, Reading, Mass.: Addison-Wesley, ISBN 978-0-201-89685-5, section 6.2.1, pp. 409–426
- ↑ Donald Knuth 1998, section 5.2.4, pp. 158–168
- ↑ Wegener, Ingo (2005), Complexity theory: exploring the limits of efficient algorithms, Berlin, New York: Springer-Verlag, p. 20, ISBN 978-3-540-21045-0
- ↑ Mohr, Hans & Schopfer, Peter (1995), Plant physiology, Berlin, New York: Springer-Verlag, ISBN 978-3-540-58016-4, chapter 19, p. 298
- ↑ Eco, Umberto (1989), The open work, Harvard University Press, ISBN 978-0-674-63976-8, section III.I
- ↑ Sprott, Julien Clinton (2010), Elegant Chaos: Algebraically Simple Chaotic Flows, New Jersey: World Scientific, ISBN 978-981-283-881-0, <https://books.google.com/books?id=buILBDre9S4C>, section 1.9
- ↑ Helmberg, Gilbert (2007), Getting acquainted with fractals, De Gruyter Textbook, Berlin, New York: Walter de Gruyter, ISBN 978-3-11-019092-2
- ↑ Breiman, Leo (1992), Probability, Classics in applied mathematics, Philadelphia: Society for Industrial and Applied Mathematics, ISBN 978-0-89871-296-4, section 12.9
- ↑ Aitchison, J. & Brown, J. A. C. (1969), The lognormal distribution, Cambridge University Press, ISBN 978-0-521-04011-2, OCLC 301100935
- ↑ Jean Mathieu and Julian Scott (2000), An introduction to turbulent flow, Cambridge University Press, p. 50, ISBN 978-0-521-77538-0, <https://books.google.com/books?id=nVA53NEAx64C&pg=PA50>
- ↑ Rose, Colin & Smith, Murray D. (2002), Mathematical statistics with Mathematica, Springer texts in statistics, Berlin, New York: Springer-Verlag, ISBN 978-0-387-95234-5, section 11.3
- ↑ Tabachnikov, Serge (2005), Geometry and Billiards, Providence, R.I.: American Mathematical Society, pp. 36–40, ISBN 978-0-8218-3919-5, section 2.1
- ↑ Durtschi, Cindy; Hillison, William & Pacini, Carl (2004), "The Effective Use of Benford's Law in Detecting Fraud in Accounting Data", Journal of Forensic Accounting V: 17–34, <http://faculty.usfsp.edu/gkearns/Articles_Fraud/Benford%20Analysis%20Article.pdf>. Hozzáférés ideje: 2018-05-28 Archiválva 2017. augusztus 29-i dátummal a Wayback Machine-ben
- ↑ Bateman, P. T. & Diamond, Harold G. (2004), Analytic number theory: an introductory course, New Jersey: World Scientific, ISBN 978-981-256-080-3, OCLC 492669517, theorem 4.1
- ↑ P. T. Bateman & Diamond 2004, Theorem 8.15
- ↑ Slomson, Alan B. (1991), An introduction to combinatorics, London: CRC Press, ISBN 978-0-412-35370-3, chapter 4
- ↑ Bakshi, U. A. (2009), Telecommunication Engineering, Pune: Technical Publications, ISBN 978-81-8431-725-1, <https://books.google.com/books?id=EV4AF0XJO9wC&pg=SA5-PA1#v=onepage&f=false>, section 5.2
- ↑ Maling, George C. (2007), "Noise", in Rossing, Thomas D., Springer handbook of acoustics, Berlin, New York: Springer-Verlag, ISBN 978-0-387-30446-5, section 23.0.2
- ↑ Tashev, Ivan Jelev (2009), Sound Capture and Processing: Practical Approaches, New York: John Wiley & Sons, ISBN 978-0-470-31983-3, <https://books.google.com/books?id=plll9smnbOIC&pg=PA48#v=onepage&f=false>, p. 48
- ↑ Chui, C.K. (1997), Wavelets: a mathematical tool for signal processing, SIAM monographs on mathematical modeling and computation, Philadelphia: Society for Industrial and Applied Mathematics, ISBN 978-0-89871-384-8, <https://books.google.com/books?id=N06Gu433PawC&pg=PA180#v=onepage&f=false>, p. 180
- ↑ Goldstein, E. Bruce (2009), Encyclopedia of Perception, Encyclopedia of Perception, Thousand Oaks, CA: Sage, ISBN 978-1-4129-4081-8, <https://books.google.de/books?id=Y4TOEN4f5ZMC>, p. 355–356
- ↑ Matthews, Gerald (2000), Human performance: cognition, stress, and individual differences, Human Performance: Cognition, Stress, and Individual Differences, Hove: Psychology Press, ISBN 978-0-415-04406-6, <https://books.google.de/books?id=0XrpulSM1HUC>, p. 48
- ↑ Bradt, Hale (2004), Astronomy methods: a physical approach to astronomical observations, Cambridge Planetary Science, Cambridge University Press, ISBN 978-0-521-53551-9, section 8.3, p. 231
- ↑ Banerjee, J. C. (1994), Encyclopaedic dictionary of psychological terms, New Delhi: M.D. Publications, ISBN 978-81-85880-28-0, OCLC 33860167, <https://books.google.com/?id=Pwl5U2q5hfcC&pg=PA306&dq=weber+fechner+law#v=onepage&q=weber%20fechner%20law&f=false>, p. 304
- ↑ Nadel, Lynn (2005), Encyclopedia of cognitive science, New York: John Wiley & Sons, ISBN 978-0-470-01619-0, lemmas Psychophysics and Perception: Overview
- ↑ Welford, A. T. (1968), Fundamentals of skill, London: Methuen, ISBN 978-0-416-03000-6, OCLC 219156, p. 61
- ↑ Paul M. Fitts (June 1954), "The information capacity of the human motor system in controlling the amplitude of movement", Journal of Experimental Psychology 47 (6): 381–391, DOI 10.1037/h0055392, reprinted in Paul M. Fitts (1992), "The information capacity of the human motor system in controlling the amplitude of movement", Journal of Experimental Psychology: General 121 (3): 262–269, doi:10.1037/0096-3445.121.3.262, <http://sing.stanford.edu/cs303-sp10/papers/1954-Fitts.pdf>. Hozzáférés ideje: 30 March 2011
- ↑ Siegler, Robert S. & Opfer, John E. (2003), "The Development of Numerical Estimation. Evidence for Multiple Representations of Numerical Quantity", Psychological Science 14 (3): 237–43, doi:10.1111/1467-9280.02438, <http://www.psy.cmu.edu/~siegler/sieglerbooth-cd04.pdf>. Hozzáférés ideje: 2015-06-02
- ↑ Dehaene, Stanislas; Izard, Véronique & Spelke, Elizabeth et al. (2008), "Log or Linear? Distinct Intuitions of the Number Scale in Western and Amazonian Indigene Cultures", Science 320 (5880): 1217–1220, DOI 10.1126/science.1156540
- ↑ Crauder, Bruce; Evans, Benny & Noell, Alan (2008), Functions and Change: A Modeling Approach to College Algebra (4th ed.), Boston: Cengage Learning, ISBN 978-0-547-15669-9, section 4.4.
- ↑ IUPAC (1997), A. D. McNaught, A. Wilkinson, ed., Compendium of Chemical Terminology ("Gold Book") (2nd ed.), Oxford: Blackwell Scientific Publications, ISBN 978-0-9678550-9-7, doi:10.1351/goldbook, <http://goldbook.iupac.org/P04524.html>
- ↑ Wright, David (2009), Mathematics and music, Providence, RI: AMS Bookstore, ISBN 978-0-8218-4873-9, chapter 5
- ↑ Ezt (és az oktávot) kivéve – ezek tiszta hangolást feltételeznek – minden a táblázatban említett hangköz adatai a kiegyenlített hangolásnak felelnek meg.
- ↑ Bird, J. O. (2001), Newnes engineering mathematics pocket book (3rd ed.), Oxford: Newnes, ISBN 978-0-7506-4992-6, section 34
- ↑ McFarland, David (2007), Quarter Tables Revisited: Earlier Tables, Division of Labor in Table Construction, and Later Implementations in Analog Computers, p. 1, <http://escholarship.org/uc/item/5n31064n>
- ↑ Robson, Eleanor. Mathematics in Ancient Iraq: A Social History, 227. o. (2008). ISBN 978-0691091822
- ↑ Gupta, R. C. (2000), "History of Mathematics in India", in Hoiberg, Dale & Ramchandani, Indu, Students' Britannica India: Select essays, Popular Prakashan, p. 329
- ↑ Stifelio, Michaele (1544), Arithmetica Integra, Nürnberg: Iohan Petreium, <https://books.google.com/books?id=fndPsRv08R0C&pg=RA1-PT419>
- ↑ Bukhshtab, A.A..szerk.: Michiel Hazewinkel: Arithmetic, Encyclopedia of Mathematics. Springer Science+Business Media B.V. / Kluwer Academic Publishers. A/a013260 (2001). ISBN 978-1-55608-010-4
- ↑ Vivian Shaw Groza and Susanne M. Shelley (1972), Precalculus mathematics, New York: Holt, Rinehart and Winston, p. 182, ISBN 978-0-03-077670-0, <https://books.google.com/?id=yM_lSq1eJv8C&pg=PA182&dq=%22arithmetica+integra%22+logarithm&q=stifel>
- ↑ Napier, John (1614), Mirifici Logarithmorum Canonis Descriptio, Edinburgh, Scotland: Andrew Hart, <http://gdz.sub.uni-goettingen.de/dms/load/img/?PPN=PPN527914568&DMDID=DMDLOG_0001&LOGID=LOG_0001&PHYSID=PHYS_0001>
- ↑ Hobson, Ernest William (1914), John Napier and the invention of logarithms, 1614, Cambridge: The University Press, <http://www.archive.org/details/johnnapierinvent00hobsiala>
- ↑ Bürgi, Jost (1620), Arithmetische und Geometrische Progress Tabulen …, Prága: Prágai Egyetemi Nyomda, <http://daten.digitale-sammlungen.de/~db/0008/bsb00082065/images/index.html?id=00082065&fip=eayaxsewqxsfsdreayasdassdassdasen&no=5&seite=7> Gieswald, Hermann Robert (1856), Justus Byrg als Mathematiker, und dessen Einleitung zu seinen Logarithmen, Danzig, Poroszország: St. Johannisschule, pp. 26 ff., <https://books.google.com/books?id=xPhSAAAAcAAJ&pg=PA26#v=onepage&q&f=false>
- ↑ Boyer 1991, Chapter 14, section "Jobst Bürgi"
- ↑ Gladstone-Millar, Lynne (2003), John Napier: Logarithm John, National Museums Of Scotland, ISBN 978-1-901663-70-9, p. 44
- ↑ Napier, Mark (1834), Memoirs of John Napier of Merchiston, Edinburgh: William Blackwood, <https://books.google.com/books?id=husGAAAAYAAJ&pg=PA1&source=gbs_toc_r&cad=4#v=onepage&q&f=false>, p. 392.
- ↑ William Harrison De Puy: The Encyclopædia Britannica: a dictionary of arts, sciences, and general literature ; the R.S. Peale reprint. 17. kötet. 9. kiad. Chicago: Werner. 1893. 179. o.
- ↑ Maor, Eli (2009), e: The Story of a Number, Princeton University Press, ISBN 978-0-691-14134-3, section 2
- ↑ a b Solutio problematis a R.P. Marino Mersenne Minimo propositi … [Solution to a problem proposed by the reverend father Marin Mersenne, member of the Minim order … ], (Antwerp, (Belgium): Johannes and Jakob Meursius, 1649). Sarasa's critical finding occurs on page 16
- ↑ R. P. Gregorio: Quadraturae circuli. 2. kiad. Antwerpen: apud Ioannem et Iacobum Meursios. 1647. 586. o. Hozzáférés: 2018. június 1.
- ↑ J. J. O'Connor & E. F. Robertson (September 2001), The number e, The MacTutor History of Mathematics archive, <http://www-history.mcs.st-and.ac.uk/HistTopics/e.html>. Hozzáférés ideje: 2009-02-02
- ↑ Cajori, Florian (1991), A History of Mathematics (5th ed.), Providence, RI: AMS Bookstore, ISBN 978-0-8218-2102-2, <https://books.google.com/?id=mGJRjIC9fZgC&printsec=frontcover#v=onepage&q=speidell&f=false>, p. 152
- ↑ a b Maor 2009, sections 1, 13
- ↑ Eves, Howard Whitley (1992), An introduction to the history of mathematics (6th ed.), The Saunders series, Philadelphia: Saunders, ISBN 978-0-03-029558-4, section 9-3
- ↑ Boyer, Carl B. (1991), A History of Mathematics, New York: John Wiley & Sons, ISBN 978-0-471-54397-8, p. 484, 489
- ↑ Bryant, Walter W., A History of Astronomy, London: Methuen & Co, <http://archive.org/stream/ahistoryastrono01bryagoog#page/n72/mode/2up>, p. 44
- ↑ Campbell-Kelly, Martin (2003), The history of mathematical tables: from Sumer to spreadsheets, Oxford scholarship online, Oxford University Press, ISBN 978-0-19-850841-0, section 2
- ↑ Abramowitz, Milton & Stegun, Irene A., eds. (1972), Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables (10th ed.), New York: Dover Publications, ISBN 978-0-486-61272-0, section 4.7., p. 89
- ↑ Spiegel, Murray R. & Moyer, R.E. (2006), Schaum's outline of college algebra, Schaum's outline series, New York: McGraw-Hill, ISBN 978-0-07-145227-4, p. 264
Fordítás[szerkesztés]
- Ez a szócikk részben vagy egészben a Logarithm című angol Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.































![{\displaystyle {\begin{aligned}\log _{a}xy&=\log _{a}x+\log _{a}y\\\log _{a}{\frac {x}{y}}&=\log _{a}x-\log _{a}y\\\log _{a}x^{k}&=k\cdot \log _{a}x\\\log _{a}{\sqrt[{p}]{x}}&={\frac {\log _{a}x}{p}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c94723c52bf5efc63cc9e2679762f284f82c1c01)





























































![{\displaystyle \ln x=\lim _{n\to \infty }n\left({\sqrt[{n}]{x}}-1\right)=\lim _{n\to \infty }n\left(1-{\frac {1}{\sqrt[{n}]{x}}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7901ca277e9fe1a5be535f262d7d4a84fc51a3f)














































![{\displaystyle {\frac {466}{440}}\approx {\frac {493}{466}}\approx 1{,}0595\approx {\sqrt[{12}]{2}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/679d073d5f5ec1a7b9596b46d7d439f9a5258f8e)



![{\displaystyle {\begin{aligned}2^{\frac {4}{12}}&={\sqrt[{3}]{2}}\\&\approx 1{,}2599\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b65ac2ebb5d2791933998b00e1e8f8854e7b302f)


![{\displaystyle \log _{\sqrt[{12}]{2}}(r)=12\log _{2}(r)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/173477b6bc89e2396abacc83ca5015ac01b0747b)






![{\displaystyle \log _{\sqrt[{1200}]{2}}(r)=1200\log _{2}(r)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a1ccc3b05bf5ae0d41f85c50ab1a7ceec4e95713)











![{\displaystyle \cos \,\alpha \,\cos \,\beta ={\frac {1}{2}}[\cos(\alpha +\beta )+\cos(\alpha -\beta )]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55be02a407ad9d4127584bd6d02f3fde6ac05fb9)










