Számtani közép
| Ezt a szócikket át kellene olvasni, ellenőrizni a szöveg helyesírását és nyelvhelyességét, a tulajdonnevek átírását. Esetleges további megjegyzések a vitalapon. |
Számtani vagy aritmetikai középértéken darab szám átlagát, azaz a számok összegének -ed részét értjük. A számtani közepet általában betűvel jelöljük:
A kiindulási értékeket összeadjuk, majd az összeget elosztjuk az összeadott számok darabszámával. A hétköznapi életben ezt egyszerűen „átlagnak” hívjuk. A matematikában a számtani közép elnevezés a mértani és a harmonikus középtől való megkülönböztetést szolgálja. Ezt a hármat pithagoraszi középnek is nevezik.
Ideálisan normális eloszlású, vagy akár csak szimmetrikus eloszlású adatok esetén a számtani közép értéke egybeesik a medián és a módusz értékével. Ha az eloszlás ferde, akkor a számtani közép nem esik egybe a mediánnal és a módusszal, tehát nem ez a leggyakoribb érték, és nem is a középső érték.
A könnyű számíthatósága és értelmezhetősége okán számos területen használják, például statisztikában, történelemben, szociológiában és pénzügyekben. Annak ellenére, hogy statisztikailag nem megfelelően jellemzi a sokaságot, az egy főre jutó jövedelmet számtani középpel számítják. Ennek oka, hogy habár közép felé húz, a számtani közép nem robusztus statisztika, mivel erősen hatnak rá a kilógó adatok, például a kevés magas jövedelem felhúzza a számtani közepet. Ezek hatása csökkenthető a kiugró értékek kiszűrésével, mint például a Dixon teszt vagy a Grubbs teszt, vagy más az eloszlásnak megfelelő statisztikát és középérték-számítást kell választani.
Egy téves használat szerint, ha x és y számok, akkor bármely számtani sorozat, aminek tagjai a kettő közé esnek, nevezhető x és y számtani közepének.[1]
Értelmezés[szerkesztés]
Az a és a b számok számtani közepe akkor és csak akkor m, ha .
Legyenek független azonos eloszlású valószínűségi változók várható értékkel és szórással, ekkor az középérték szintén körül ingadozik, és szórása kisebb, mint . Ha tehát egy valószínűségi változó várható értéke és szórása is véges, akkor a Csebisev-egyenlőtlenség miatt a mintaközép a minta elemszámának növelésével sztochasztikusan konvergál a valószínűségi változó várható értékéhez. Tehát a számtani közép alkalmas a várható érték becslésére, viszont érzékeny a nem tipikus adatokra (lásd: medián).
A számtani középre vonatkozó alaptétel[szerkesztés]
Tétel: Ha valós számok, és , vagyis az és számok számtani közepe, akkor . Szemléletesen ez azt jelenti, hogy az és a számoktól egyenlő távolságra (vagyis „középen”) helyezkedik el a számegyenesen. Valóban, hiszen ha , akkor és .
Adott valós számok számtani középértéke nem lehet kisebb, mint a számok legkisebbike, és nem lehet nagyobb, mint a számok legnagyobbika:
Algebrai tulajdonságok[szerkesztés]
Ha a tetszőleges számsorozatot tetszőlegesen hosszan bővítjük e számok számtani közepével, akkor az így kibővített sorozat tagjainak számtani középértéke megegyezik az eredeti számtani középpel:
A számtani és mértani közép közötti egyenlőtlenség:
Mivel középre húz, alkalmas a centrális tendencia mérésére. Ezek közé tartozik, hogy:
- Ha az számok számtani közepe , akkor . Ezt azzal szemléltetik, hogy a számtani középtől balra és jobbra levő számok ellensúlyozzák egymást. A számtani közepet egyértelműen meghatározza ez a tulajdonsága, tehát nincs más ilyen tulajdonságú szám.
- Ha az számokat egyetlen paraméterrel kell jellemezni, akkor erre a számtani közép a legalkalmasabb, mivel minimalizálja a négyzetes eltéréseket a paramétertől. Ezt a minta négyzetes hibájának, vagy torzított tapasztalati szórásnégyzetnek nevezik.[2] A számtani közép (ilyen kontextusban tapasztalati várható érték) torzítatlanul közelíti a minta várható értékét.
Szembeállítás a mediánnal[szerkesztés]
A számtani közép szembeállítható a mediánnal. A medián definíció szerint a minta középső eleme, tehát az elemek fele kisebb, fele nagyobb nála. Páros elemszám esetén a medián a két középső elem számtani közepe. A számtani közép és a medián akkor esik egybe, ha a rendezett sorozat számtani. Például, ha a rendezett sorozat akkor a számtani közép és a medián is 2,5. Ha például , akkor a számtani közép 6,2, de a medián 4. A számtani közép lehet sokkal nagyobb, vagy kisebb is, mint a sorozat legtöbb eleme.
A medián és a számtani közép együttes használata elterjedt. Statisztikai elemzések szerint az 1980-as évektől az Amerikai Egyesült Államokban a jövedelem számtani közepe gyorsabban nőtt, mint a mediánja.[3]
Számtani sorozatok[szerkesztés]
Számtani sorozatban – az elsőt kivéve – bármelyik tag a két szomszédjának számtani közepe. Általában tag az és tagok számtani közepe, ha pozitív egészek. Ennek megfordítása is igaz (ha egy sorozatban bármely két tag a szomszédos tagok számtani közepe, akkor az egy számtani sorozat), mégpedig egyszerű következménye a számtani középre vonatkozó alaptételnek.
Súlyozott számtani közép[szerkesztés]
A számtani középnek súlyozott változata is értelmezhető. Alkalmazzák például a keverési feladatokban, a valószínűségszámításban és a statisztikában.
A súlyozott számtani közép számítása:
- .
ahol az számok rendre a súlyokkal szerepelnek.
A keverési feladatokban jelöli a koncentrációt vagy a hőmérsékletet, és a térfogatot, vagy a tömeget.
A statisztikai alkalmazásokban az adatpontokhoz tartozó súlyok azt mutatják, hogy az adott adatpont hányszor jelenik meg a mintában.
Több minta összetevésekor az egyes minták középértékeit a megfelelő minták elemszámával súlyozzák.
A valószínűségszámításban, ha az valószínűségi vektorváltozók közös várható értéke , de szórásuk rendre , akkor a súlyozott középérték körül ingadozik, és szórásnégyzete
- .
Ha most , akkor
- .
A Cauchy–Bunyakovszkij–Schwarz-egyenlőtlenség alapján
- .
A választás minimalizálja a középérték szórását. A súlyok választása mutatja, hogy melyik adatnak mekkora fontosságot tulajdonítunk.
Alkalmazás[szerkesztés]
A számtani közepet additív – magyarul összeadható – mennyiségek átlagolására használjuk (például magasságok átlaga, testsúlyok átlaga stb.).
Függvény középértéke[szerkesztés]
A Riemann-integrálható függvények középértéke a számtani közép általánosításaként fogható fel.
Az Riemann-integrálható függvény középértéke
Ha most egyenlő osztásközöket veszünk, ahol osztópontok, és a két szomszédos osztópont közötti távolság , akkor az
számtani közép tart az középértékhez.
Ha f folytonos, akkor az integrálszámítás középértéktétele szerint létezik , amire , a függvény legalább egy helyen felveszi középértékét.
A középértéknek is van súlyozott változata, ahol is a súlyfüggvény pozitív minden -re. Ekkor a súlyozott középérték
- .
Az mértéktérben, ahol , a Lebesgue-integrálható függvények középértéke
- .
Valószínűségi tér esetén, ahol , a középérték az
alakra hozható, ami éppen az f(x) várható értéke.
Folytonos valószínűségi eloszlások[szerkesztés]
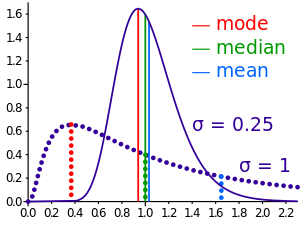
Valószínűségi eloszlások esetén annak a valószínűsége, hogy az érték a számegyenes melyik szakaszára esik, különbözhet attól, hogy az érték egy másik, de ugyanolyan hosszú szakaszra esik. Egyenlőség minden szakaszpárra csak geometriai eloszlás esetén áll fenn. A többi esetet eloszlásfüggvénnyel vagy sűrűségfüggvénnyel írják le. A súlyozott átlag megfelelője itt a valószínűségeloszlás várható értéke. A valószínűségeloszlás folytonos, ha eloszlásfüggvénye folytonos. A sűrűségfüggvény létezéséhez az eloszlásfüggvénynek differenciálhatónak kell lennie. Az egyik leggyakrabban használt eloszlásfüggvény a normális eloszlás, ami szimmetrikus a várható értékére, így mediánja és módusza is a várható értéke. Nem szimmetrikus eloszlások esetén ezek különböznek. Egy gyakran használt nem szimmetrikus (ferde) a lognormális eloszlás, amit az ábra is mutat.
Szögek[szerkesztés]
Szögek és más hasonló mennyiségek, egy modulus szerinti mennyiségek átlagolására alkalmatlan a számtani közép. Az egyik nehézség az, hogy a két mennyiségnek két távolsága van, amelyek közül a kisebbet szokták távolságon érteni, de a számtani közép lehet, hogy a nagyobb távolságot felezi. Például, ha a két mennyiség 1 és 359 fok, akkor a hagyományos számtani közép 180 fokot ad, pedig a 0 vagy 360 foknak geometriai jelentése is lenne. Egy másik probléma az, hogy a modulo mennyiségek értelmezhetők többféleképpen is. Például 1 és 359 fok helyett lehetne 1 és -1 fok, de lehetne 361 és 719 fok is, ami több különböző eredményt ad. Éppen ezért ezekre a mennyiségekre át kell definiálni a számtani közepet, hogy a moduláris távolságot felezze. Az így definiált mennyiség a moduláris számtani közép, vagy moduláris átlag.
Kapcsolat más közepekkel[szerkesztés]
Legyen egy intervallumon értelmezett szigorúan növő folytonos függvény. Legyenek továbbá adva a súlyok. Ekkor az számok -vel súlyozott kváziaritmetikai közepe
- .
Nyilván
- .
Így a különböző f függvényekkel különböző közepek definiálhatók. visszaadja a számtani közepet, a mértani közepet, és a k-adik hatványközepet.
Mindezek a közepek függvényekre is általánosíthatók. Ehhez azt kell még kikötni, hogy az f függvény értelmezési tartománya tartalmazza az u függvény képhalmazát. Ekkor az u függvény középértéke:
Kapcsolódó szócikkek[szerkesztés]
- Kváziaritmetikai közép (általánosítás)
- A számtani és mértani közép közötti egyenlőtlenség
- A számtani és négyzetes közép közötti egyenlőtlenség
Jegyzetek[szerkesztés]
- ↑ Foerster, Paul A.. Algebra and Trigonometry: Functions and Applications, Teacher's Edition, Classics, Upper Saddle River, NJ: Prentice Hall, 573. o. (2006). ISBN 0-13-165711-9
- ↑ Medhi, Jyotiprasad. Statistical Methods: An Introductory Text. New Age International, 53–58. o. (1992). ISBN 9788122404197
- ↑ Paul Krugman, "The Rich, the Right, and the Facts: Deconstructing the Income Distribution Debate", 'The American Prospect'
Források[szerkesztés]
Fordítás[szerkesztés]
Ez a szócikk részben vagy egészben az Arithmetic mean című angol Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.










































![{\displaystyle f:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b592d102ccd1ba134d401c5b3ea177baaba3ffac)





![{\displaystyle \xi \in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6cc05d1fb45b90e25c99bc6a57473d508d3e9c23)


![{\displaystyle x\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/026357b404ee584c475579fb2302a4e9881b8cce)















