Szögfüggvények
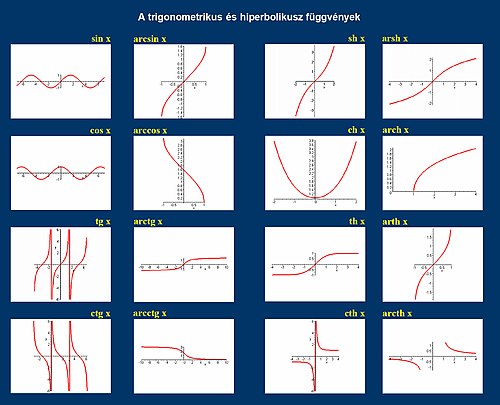
A trigonometrikus függvények vagy szögfüggvények eredetileg egy derékszögű háromszög egy szöge és két oldalának hányadosa közötti összefüggést írják le (innen nyerték magyar és latin nevüket is). A szögfüggvények fontosak többek között a geometriai számításoknál, különféle mozgások (harmonikus rezgőmozgás, körmozgás) és a periodikus jelenségek leírásánál, és a műszaki élet számtalan területén.
A szögfüggvények a derékszögű háromszög két oldalának hányadosa és a szög összefüggésén kívül az egységsugarú körben tekintett forgásszög-végpontok metszeteivel (vetületeivel, koordinátáival) is definiálhatók. Ez utóbbi definíció már 90°, azaz π/2-nél nagyobb, sőt, negatív (mindent összevéve, tetszőleges valós) argumentumokra is működik.
A matematikai analízis eredményei szerint a szögfüggvények végtelen sorként vagy bizonyos differenciálegyenletek megoldásaként is meghatározhatóak. Ily módon már komplex számokra is értelmezhetőek. Mindezeket alább bemutatjuk.
Hagyományosan hat fontos szögfüggvény alakult ki (ezek közül négyet használnak gyakrabban, de csak kettő tekinthető igazán alapvetőnek, a többi ezekből racionális műveletekkel kapható), melyeket az alábbi táblázat tartalmaz. A korai függvénytáblák más szögfüggvényeket is használtak, ilyen például a verszinusz (1 ‒ cos θ) és az exszekáns (sec θ ‒ 1), de ezeket manapság aligha használják.
A szögfüggvények általánosíthatók más γ alapszögekre is. Ezek definiálhatók γ szögű háromszög, és ferdeszögű koordináta-rendszer segítségével is, ahol az egységvektorok hajlásszöge π-γ. Eszerint a γ alapszög még további általánosítás esetén sem lehet π egész számú többszöröse.
| Függvény | Rövidítés | Összefüggés |
|---|---|---|
| Szinusz | sin | |
| Koszinusz | cos | |
| Tangens | tg (vagy tan) |
|
| Kotangens | ctg (vagy cot) |
|
| Szekáns | sec | |
| Koszekáns | csc (vagy cosec) |
A szögfüggvények jellemzése[szerkesztés]
Értelmezési tartomány[szerkesztés]
A szinusz és a koszinusz az egész számegyenesen értelmezett folytonos függvények. A tangens szakadási helyei π/2+kπ, a kotangensé kπ alakúak. A szekáns minden π/2+kπ, a koszekáns minden kπ pontban szakad.
Értékkészlet[szerkesztés]
A szinusz és a koszinusz korlátos függvények, értékkészletük a [-1,1] intervallum. A tangens és a kotangens az összes valós számot felveszi. A szekáns és a koszekáns értékkészletéből hiányzik a (-1,1) intervallum.
Szimmetria[szerkesztés]
A szögfüggvények periodikusak. A szinusz, a koszinusz, a szekáns és a koszekáns periódusa 2π, a tangensé és a kotangensé π.
A szögfüggvények páros vagy páratlan függvények. A szinusz, a tangens, a kotangens és a koszekáns páratlan, a koszinusz és a szekáns páros függvény.
A szögfüggvények menete[szerkesztés]
A szinusz menete: az első negyedben nő, a másodikban és harmadik csökken, a negyedikben ismét nő. A koszinusz az első és a második negyedben csökken, a harmadikban és a negyedikben nő. A tangens minden (π/2-kπ, π/2+kπ) intervallumon nő, a kotangens minden (kπ, (k+1)π) intervallumon csökken. A szekáns az első és a második negyedben nő, a harmadikban és a negyedikben csökken. A koszekáns az első negyedben csökken, a másodikban és a harmadikban nő, a negyedikben csökken.
Konvexitás[szerkesztés]
A szinusz az első két negyedben konkáv, a második kettőben konvex. A koszinusz az első negyedben konkáv, a másodikban és a harmadikban konvex, a negyedikben konkáv. A tangens és a kotangens az első negyedben konvex, a másodikban konkáv, a harmadikban konvex, a negyedikben konkáv. A szekáns az első negyedben konvex, a másodikban és a harmadikban konkáv, a negyedikben konvex. A koszekáns az első két negyedben konvex, a második kettőben konkáv.
Nevezetes pontok[szerkesztés]
A szinusznak nullhelyei vannak a kπ alakú helyeken. Ezek egyben inflexiós pontok is. Maximumhelyei a π/2+2kπ, minimumhelyei a -π/2+2kπ alakú pontok.
A koszinusz a nullát a π/2+kπ helyeken veszi fel. A 2kπ pontokban maximuma, a π+2kπ pontokban minimuma van.
A tangens nullhelyei a kπ, pólushelyei a π/2+kπ pontok. A kotangens a nullát a π/2+kπ veszi fel; a kπ helyeken pólusa van. Nullhelyeik egyben inflexiós pontok is.
A szekáns helyi minimumai a 2kπ, helyi maximumai a kπ+2kπ alakú pontok, a π/2+2kπ helyeken pólusa van.
A koszekáns helyi minimumát az 1/2π+2kπ, helyi maximumát a -1/2π+2kπ helyeken veszi fel; a kπ helyeken pólusa van.
Definíció a derékszögű háromszögben[szerkesztés]
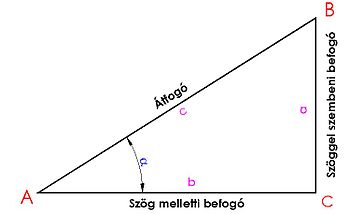
Az α szög szögfüggvényeinek definiálásához vegyünk fel egy tetszőleges ABC derékszögű háromszöget, melynek A csúcspontjában mérhető az α szög. A háromszög oldalai a következők:
- az átfogó a derékszöggel szemben lévő (leghosszabb) oldal, c-vel jelöljük,
- a szöggel szembeni oldal a szóban forgó szöggel átellenes oldal, jelölése a,
- a szög melletti oldal a szóban forgó szög mellett lévő oldal (a szög egyik szára), jelölése b.
A vizsgált háromszög az euklideszi síkban fekszik, tehát a háromszög szögeinek összege π radián (vagy 180°) és két nem derékszögű szöge nulla és π/2 radián között van. A derékszögű háromszögben a szögfüggvények csak ebben a tartományban értelmezhetők. Később a definíciót az egységsugarú kör segítségével kiterjesztjük az összes valós számra.
1) Egy szög szinusza a szöggel szembeni befogó és az átfogó hányadosa
Megjegyzendő, hogy a fenti összefüggés minden olyan derékszögű háromszögre igaz, melynek egyik szöge α, mivel minden ilyen háromszög hasonló egymáshoz.
2) Egy szög koszinusza a szög melletti oldal és az átfogó hányadosa. Esetünkben:
3) Egy szög tangense a szöggel szembeni oldal és a szög melletti oldal hányadosa:
A többi három szögfüggvényt a fenti függvényekkel definiálhatjuk.
4) A koszekáns csc(α) a sin(α) reciproka, vagyis az átfogó és a szöggel szembeni befogó hányadosa:
5) A szekáns sec(α) a cos(α) reciproka, azaz az átfogó és a szög melletti befogó hányadosa:
6) A kotangens ctg(α) a tg(α) reciproka, azaz a szög melletti és a szöggel szemben lévő befogó hányadosa:
Definíció az egységsugarú kör ill. az egységvektor segítségével[szerkesztés]

A hat szögfüggvény az egységsugarú kör segítségével is meghatározható. Ez a definíció lehetővé teszi, hogy a szögfüggvényeket ne csak a 0 és π/2 radián (0°-90°) szögtartományra értelmezzük, hanem kiterjesszük az összes pozitív és negatív szögre (valós értékre). Az egységsugarú kör ugyanakkor könnyen használható vizuális segédeszköz is a szögfüggvényeket értelmező összes derékszögű háromszög megmutatására.
A képen néhány nevezetes szög van feltüntetve radiánban mérve. A kör középpontjától jobbra húzott egyenes jelenti a 0 radián szöget. A pozitív szögek másik szára ettől az óramutató járásával ellenkező irányban, míg a negatív szögek másik szára az óramutató járásával megegyező irányban helyezkednek el. A kör középpontjában vegyünk fel egy derékszögű koordináta-rendszert. Ha felrajzolunk egy derékszögű háromszöget, melynek egyik befogója az x tengelyre esik, egyik csúcspontja a középpontban van, átfogója egységnyi, vagyis az egységsugarú kör sugara és a középpontban lévő szög α, akkor az átfogó kör kerületére eső pontjának x koordinátája cos α, y koordinátája pedig sin α lesz. Mivel az átfogó egyenlő a sugárral és így hossza egységnyi, írható: sin α = y/1 és cos α = x/1.




2π-nél nagyobb vagy -2π-nél kisebb szögek esetén a szög szára tovább folytathatja elfordulását a középpont körül. Így látható, hogy a szinusz- és koszinuszfüggvény 2π szerint periodikus függvény:
minden α szögre és minden k egész számra.
A szinusz, koszinusz, szekáns és koszekáns függvények legkisebb periódusa a teljes kör, vagyis 2π radián vagy 360°, a tangens- és kotangensfüggvények legkisebb periódusa egy félkör, vagyis π radián vagy 180°.
A fentiekben csak a szinusz- és koszinuszfüggvények definíciója szerepelt az egységsugarú körben, a többi négy szögfüggvény így definiálható:
- ;
A tangensfüggvény grafikonja jelentősen eltér a szinusz- és koszinuszfüggvényétől. A tangens x tengellyel való metszéspontjai megfelelnek azoknak az x értékeknek, melyeknél a szinusz metszi az x tengelyt, szakadása pedig pontosan azon x helyeken van, ahol cos(x) értéke 0. A függvényértékek lassan változnak kπ szögek környékén, de nagyon gyors a változás (k + 1/2)π környékén. A tangensfüggvénynek minden (k + 1/2)π értéknél függőleges aszimptotája van. Ennek az az oka, hogy a függvényérték végtelenhez tart, ha a független változó (x) balról tart (k + 1/2)π-hez és mínusz végtelenhez, ha x jobbról tart (k + 1/2)π-hez.
Az összes többi szögfüggvény is ábrázolható az O középpontú egységsugarú kör segítségével, és régebben így is definiálták. Például a kör AB húrjához tartozó középponti szög fele θ, Indiában a sin(θ)-t az AC távolsággal definiálták először. Az OC vízszintes szakasz cos(θ), versin(θ) = 1 ‒ cos(θ) pedig a CD távolság. Az érintőn kijelölt AE szakasz hossza pedig tg(θ), innen a szögfüggvény neve (tangens = érintő). Az OE távolság a sec(θ) és csc(θ) = OF. DE sz exszekáns: exsec(θ) = sec(θ) ‒ 1. Az ábrából látható, hogy a szekáns- és tangensfüggvénynek szakadása van θ = π/2-nél (90°-nál), a koszekánsnak és a kotengensnek pedig θ = 0-nál. (Sok hasonló ábra szerkesztése lehetséges és a szögfüggvények közötti alapvető összefüggések geometriailag is igazolhatók.)
Definíció végtelen sorral[szerkesztés]

Csak geometriát és a határérték tulajdonságait használva igazolni lehet, hogy a szinuszfüggvény deriváltja a koszinuszfüggvény és a koszinuszfüggvény deriváltja a mínusz szinusz. (Itt és a továbbiakban a szög értéke mindig radiánban értendő). Ezek után felírható a szögfüggvények Taylor-sora:
Ezeket az összefüggéseket néha a szinusz- és koszinuszfüggvény definíciójának tekintik. Gyakran használják ezeket a szögfüggvények szigorúbb vizsgálata alapjának, (például a Fourier-sorok esetében) mivel a végtelen sorok elméletét a valós számok rendszere alapján lehet levezetni minden geometriai vonatkozástól függetlenül. Ezeknek a függvényeknek a differenciálhatósága és folytonossága levezethető egyedül a sorok tulajdonságaiból. Sokszor csak a szinuszt és a koszinuszt adják meg így, a többi szögfüggvényt hányadosokként, vagy reciprokként definiálják.
A szinusz és a koszinusz deriváltjai alapján hányadosszabállyal a többi szögfüggvény deriváltja is meghatározható:
- a tangens deriváltja
- a kotangens deriváltja
- a szekáns deriváltja
- a koszekáns deriváltja
A tangens hatványsora a nulla π/2 sugarú környezetében konvergens:[1]
ahol az n-edik Bernoulli-szám.
A kotangens hatványsora a nulla π sugarú környezetében konvergál:[2]
A szekáns hatványsora:
A koszekánsé:
Összefüggés az exponenciális függvénnyel és a komplex számokkal[szerkesztés]
Igazolni lehet a végtelen sor definíció segítségével, hogy a szinusz-, illetve koszinuszfüggvény a komplex exponenciális függvény képzetes és valós részei, ha az argumentum tisztán képzetes:
Ezt az összefüggést először Euler mutatta ki, és a képletet Euler-formulának hívják. Ilyen módon a szögfüggvények alapvetően fontosak lettek a komplex analízis geometriai interpretációjában. Ha az egységsugarú kört a komplex síkon az eix egyenlettel adjuk meg, másrészt a kör paraméteres alakját nézzük, az összefüggés a komplex exponenciális függvény és a szögfüggvények között nyilvánvaló lesz.
A trigonometrikus függvényeknek ezt a definícióját alkalmazva z komplex argumentumokra:
ahol i2 = ‒1. Hasonlóan valós x-re:
Kapcsolat a hiperbolikus függvényekkel[szerkesztés]
A szögfüggvények és a hiperbolikus függvények közötti kapcsolat:
ahol a Gudermann-függvény.
Definíció differenciálegyenletekkel[szerkesztés]
Mind a szinusz-, mind a koszinuszfüggvény kielégíti az alábbi differenciálegyenletet:
A kétdimenziós V vektortéren belül, mely az egyenlet összes megoldását tartalmazza, a szinuszfüggvény az egyetlen megoldás, amely kielégíti az y(0) = 0 és y′(0) = 1 kezdeti feltételeket, a koszinuszfüggvény pedig az egyetlen megoldás, amely kielégíti az és kezdeti feltételeket. Ez a definíció teljesen egyenértékű az Euler-formulával. Ez a differenciálegyenlet nemcsak a szinusz és koszinusz definíciójára használható, hanem alkalmas arra is, hogy segítségével igazolhatók legyenek a szinusz- és koszinuszfüggvényre felírható azonosságok is.
A tangensfüggvény az egyetlen, mely kielégíti az alábbi nemlineáris differenciálegyenletet:
az y(0) = 0 kezdeti feltétellel.
Komplex szögfüggvények[szerkesztés]
A szinusz és a koszinusz hatványsoruk, az Euler-formula, vagy differenciálegyenlet segítségével regulárisan kiterjeszthető a komplex számsíkra. Ezzel a kiterjesztéssel nem lesznek újabb zérushelyek, és továbbra is teljesülnek a függvényegyenletek, de a korlátosság elvész.
A többi szögfüggvény kiterjesztését a szinusz és a koszinusz segítségével végzik; ezzel a függvényegyenletek továbbra is megmaradnak, és nem keletkeznek újabb pólusok, vagy nullhelyek sem.
Inverz függvények[szerkesztés]
A trigonometriai függvények periodikusak, ezért nem injektívek, tehát szigorú értelemben véve nincs inverz függvényük. Az inverz függvény definiálásához ezért le kell szűkíteni az értelmezési tartományukat olyan módon, hogy a trigonometriai függvény bijektív legyen. Az alábbiakban a bal oldalon szereplő függvények definíciója a jobb oldalon szereplő egyenlet. A legfontosabb inverz függvények:
| Név | Jelölés | Definíció | Értelmezési tartomány | Értékkészlet (radián) |
Értékkészlet (fok) |
|---|---|---|---|---|---|
| arkuszszinusz | y = arcsin(x) | x = sin(y) | −1 ≤ x ≤ 1 | ≤ y ≤ | −90° ≤ y ≤ 90° |
| arkuszkoszinusz | y = arccos(x) | x = cos(y) | −1 ≤ x ≤ 1 | 0 ≤ y ≤ | 0° ≤ y ≤ 180° |
| arkusztangens | y = arctan(x) | x = tan(y) | < y < | −90° < y < 90° | |
| arkuszkotangens | y = arccot(x) | x = cot(y) | 0 < y < | 0° < y < 180° | |
| arkuszszekáns | y = arcsec(x) | x = sec(y) | x ≤ −1 vagy 1 ≤ x | 0 ≤ y < vagy < y ≤ | 0° ≤ y < 90° vagy 90° < y ≤ 180° |
| arkuszkoszekáns | y = arccsc(x) | x = csc(y) | x ≤ −1 vagy 1 ≤ x | ≤ y < 0 vagy 0 < y ≤ | −90° ≤ y < 0° vagy 0° < y ≤ 90° |
Az inverz trigonometriai függvényeket is ki lehet fejezni végtelen sorok segítségével. Például:
Ezek a függvények integrálok formájában is felírhatóak:
Általánosított szögfüggvények[szerkesztés]
Az általánosított szögfüggvényeket a nem általánosított szögfüggvényekhez hasonlóan értelmezzük egy γ alapszögre vonatkozóan. Ezek a függvények értelmezhetők γ szögű háromszög, vagy ferdeszögű koordináta-rendszer segítségével, ahol az i, j koordinátavektorok szöge π-γ. Ha a γ alapszöget derékszögnek vesszük, akkor visszajutunk a nem általánosított szögfüggvényekhez.
Definíció a γ szögű háromszögben[szerkesztés]
A definícióban a derékszög helyét átveszi a γ szög, az átfogóét a γ szöggel szemközti c oldal, a szöggel szemközti befogóét a szöggel szemben fekvő oldal, és a szög mellett levő befogóét a szög melletti oldal.
Így
1) Egy szög γ alapszögű szinusza a szöggel szembeni oldal és a γ szöggel szemközti oldal hányadosa
Megjegyzendő, hogy a fenti összefüggés minden olyan háromszögre igaz, melynek egyik szöge γ, másik szöge α, mivel minden ilyen háromszög hasonló egymáshoz.
2) Egy szög γ alapszögű koszinusza a szög melletti oldal és a γ szöggel szemközti oldal hányadosa. Esetünkben:
3) Egy szög γ alapszögű tangense a szöggel szembeni oldal és a szög melletti oldal hányadosa:
A többi három szögfüggvényt a fenti függvényekkel definiálhatjuk.
4) A γ alapszögű koszekáns cscγ(α) a sinγ(α) reciproka, vagyis a γ szöggel szemközti oldal és a szöggel szembeni oldal hányadosa:
5) A γ alapszögű szekáns secγ(α) a cosγ(α) reciproka, azaz a γ szöggel szemközti oldal és a szög melletti oldal hányadosa:
6) A γ alapszögű kotangens ctgγ(α) a tgγ(α) reciproka, azaz a szög melletti és a szöggel szemben lévő oldal hányadosa:
Az egységsugarú kör és ferdeszögű koordináta-rendszer segítségével[szerkesztés]
A nem általánosított szögfüggvényekhez hasonlóan az általánosított szögfüggvények is kiterjeszthetők a valós számokra. Az eltérés csak annyi, hogy a γ alapszögű szinusz és a koszinusz az elforgatott egységnyi hosszúságú vektor ferdeszögű koordinátáival egyezik meg a π-γ szögű koordináta-rendszerben. A többi szögfüggvény a nem általánosított esethez hasonlóan hányadosként vagy reciprokként definiálható.
2π-nél nagyobb vagy -2π-nél kisebb szögek esetén a szög szára tovább folytathatja elfordulását a középpont körül. Így látható, hogy a γ alapszögű szinusz- és koszinuszfüggvény is 2π szerint periodikus függvény.
Összefüggések[szerkesztés]
Szinusztétellel belátható, hogy:
A többi szögfüggvényre teljesül:
Az összefüggések segítségével kiszámíthatók az általánosított szögfüggvények értékei.
Példa:
Alkalmazás[szerkesztés]
Az általános szögfüggvényekkel egyszerűsödik a háromszögek megoldása, és a ferdeszögű vektorkoordináták kiszámítása.
Lásd még[szerkesztés]
Források[szerkesztés]
- Bárczy Barnabás: Trigonometria
- Hajnal Imre: Matematika II.
- Hajnal Imre: Matematika III.
- Halász Gábor: Komplex függvénytan
- Négyjegyű függvénytáblázat
- Obádovics J. Gyula: Matematika
- Szekáns és koszekáns a MathWorldnél
- Általános szögfüggvények a Sulineten
Jegyzetek[szerkesztés]
- ↑ Milton Abramowitz-Irene Stegun: Handbook of Mathematical Functions, (1964) Dover Publications, New York. ISBN 0-486-61272-4 4.3.67 Archiválva 2009. március 31-i dátummal a Wayback Machine-ben
- ↑ Milton Abramowitz-Irene Stegun: Handbook of Mathematical Functions, (1964) Dover Publications, New York. ISBN 0-486-61272-4 4.3.70 Archiválva 2009. március 31-i dátummal a Wayback Machine-ben
- ↑ Inczeffy Szabolcs: A trigonometrikus függvények általános alakjai, in: A matematika tanítása, 1995., III. évf./3. szám.
























































