Vektortér

Vektorok összeadása és skalárral szorzása: Egy v vektort (kékkel) hozzáadunk a w vektorhoz (pirossal, alul). Fent a w vektort 2-szeresére nyújtjuk, az eredmény a v + 2·w összeg

A vektortér, más néven lineáris tér a lineáris algebra egyik legalapvetőbb fogalma, amelyhez a geometriában (is) használt vektor fogalmának általánosítása vezet. A vektorokkal végezhető műveletek legelemibb tulajdonságait axiomatikusan definiálja, ezáltal egy algebrai struktúra-típus keletkezik. A lineáris tér a mi szokásos síkunk és terünk általánosítása többdimenziós terekre. Jelentősége nem csupán elméleti, a fizikában, informatikában, a komputergrafikában, számos más elméleti és alkalmazott tudományágban; nemkülönben a matematika számos területén fontos szerepet játszik.

Formális definíció

Vektorok összeadása: a v (kékkel) és a w (pirossal) v + w összege feketével

Skalárral szorzás: a v vektor és ellentettje, −v kékkel; a w vektor pirossal, és 2w rózsaszínnel

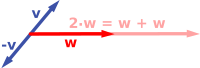
Legyen F egy test. Egy V nemüres halmazt vektortérnek nevezünk az F test felett, ha

• V halmazon értelmezve van egy összeadás nevű művelet, V × V → V függvény, ∀ u, v ∈ V elempárhoz hozzárendel egy és csak egy V-beli elemet (u+v), valamint
• F és V között értelmezve van egy skalárral való szorzás nevű művelet, F × V → V függvény, ∀ λ ∈ F és v ∈ V elempárhoz egyértelműen hozzárendel egy V-beli elemet (λv),

úgy, hogy az alábbi azonosságok, úgynevezett vektortér-axiómák teljesülnek:

1. V az összeadásra nézve kommutatív csoportot, Abel-csoportot alkot, azaz az összeadás:
   • asszociatív: ∀ u, v, w ∈ V: u + (v + w) = (u + v) + w.
   • kommutatív: ∀ u, v ∈ V: u + v = v + u.
   • létezik neutrális elem: 0 ∈ V, V nullvektora: v + 0 = v, ∀ v ∈ V.
   • invertálható: ∀ v ∈ V: ∃ olyan -v ∈ V additív inverz: v + (-v) = 0.
2. Skalárral való szorzás disztributivitási szabályai:
   • ∀ λ ∈ F és u, v ∈ V: λ(u + v) = λu + λv. (disztributivitási szabály)
   • ∀ λ, μ ∈ F és v ∈ V: (λ + μ)v = λv + μv.(disztributivitási szabály)
   • ∀ λ, μ ∈ F és v ∈ V: λ(μv) = (λμ)v. (asszociativitási szabály)
   • ∀ v ∈ V: 1v = v, ahol 1 az F test egységeleme.

Formálisan tehát úgy definiálhatjuk a vektortereket, figyelembe véve, hogy $\mathbf {F} =\langle F,+,-,0,\cdot ,1\rangle$ egy test,
az F feletti vektortér egy algebrai struktúra, a következő formában

$\mathbf {V} =\langle V,\oplus ,-\!\!-,\mathbf {0} ,F,+,-,0,\cdot ,1,\star \rangle$

úgy, hogy

$\langle V,\oplus ,-\!\!-,\mathbf {0} \rangle$ Abel-csoport,

$\star :F\times V\mapsto V$ skalárral való szorzás, melyre teljesülnek a fent említett disztributivitási szabályok.

Ekkor a V vektortér struktúráját a következőképpen is jelölhetjük

$\langle V,\oplus ,-\!\!-,\mathbf {0} ,\mathbf {F} ,\star \rangle$

V elemeit vektoroknak, F elemeit skalároknak nevezzük.
Megkülönböztetünk úgynevezett speciális vektortereket is, amelyeken még egyfajta szorzás is értelmezett.
Ilyenek például a skaláris szorzattal ellátott euklideszi terek.

Elemi tulajdonságok

V Abel-csoport

• nullvektor és az additív inverz unicitása,
• bármely u,v,w,t ∈ V: az u+x = v, és y+w = t egyenletek egyértelműen megoldhatók V-ben x és y-ra,
• összeadás asszociativitása és kommutativitása miatt többtagú összegek esetén a zárójelezés és a tagok sorrendje is tetszőlegesen megváltoztatható.

További következmények

• bármely λ ∈ F: λ0 = 0,
• bármely v ∈ V: 0v = 0, ahol 0 az F test nulleleme,
• bármely v ∈ V: (-1)v = -v, ahol -1 az F test egységelemének additív inverze,
• ha λv = 0, akkor λ = 0 vagy v = 0.
• (-λ)v = -(λv) = λ(-v)

Példák

Példa függvények összeadására: a szinuszfüggvény és az exponenciális függvény $\sin +\exp \colon \mathbb {R} \to \mathbb {R}$ összege, $(\sin +\exp )(x)=\sin(x)+\exp(x)$

A lineáris tér egy nagyon általános fogalom, rengeteg példa van rá a matematikában. Nagyon sok olyan matematikai fejezetben is megjelenik, amit szerteágazóan alkalmaznak a fizika számos területén, például a funkcionálanalízis vagy éppen a differenciálgeometria, hogy csak néhányat említsünk.

• a közönséges síkbeli és térbeli, origóból kiinduló vektorok a valós test felett a szokásos vektorösszeadásra és skalárral való szorzásra nézve,
• a valós szám n-esek $\mathbb {R}$ felett, a komplex szám n-esek $\mathbb {C}$ felett, és
• általában F ⁿ, F felett (F tetszőleges test), a szokásos módon értelmezett, komponensenként végzett műveletekre; ezeket a vektorokat általában oszlopvektorként ábrázolják,
• F ^{n × k}, F felett, azaz az n×k-as mátrixok F test felett, a mátrixok szokásos, komponensenkénti összeadására és skalárral való szorzására nézve.
• F [x], azaz az F feletti polinomok, F felett, a polinomok összeadására és skalárral való szorzására nézve,
• a legfeljebb n-edfokú polinomok F felett,
• valós számsorozatok a valós test felett a szokásos műveletekre,
• az $\left[a,b\right]$ intervallumon folytonos $\mathbb {R}$-be képező függvények a valós test felett, a szokásos pontonkénti összeadásra, és skalárral való szorzásra nézve,
• az $\left[a,b\right]$ intervallumon Riemann-integrálható $\mathbb {R}$-be képező függvények a valós számok teste felett, a szokásos pontonkénti összeadásra, valamint a skalárral való szorzásra nézve,
• a komplex számok a valós test felett, a komplex számok körében értelmezett műveletekre,
• a komplex számok a komplex számok teste felett,
• a valós számok a valós számok teste felett,
• a komplex számok a valós számok felett,
• a valós számok a racionális számok felett,
• általában, testbővítés esetén a bővebb test a szűkebb felett,
• a valószínűségi változók a szokásos összeadásra és skalárral való szorzásra nézve,
• az euklideszi sík, illetve tér eltolásai, hiszen az eltolások egymás utáni végzése megfelel a vektorok összeadásának, és a skalárszoros eltolás megfelel az eltolásvektor skalárszorosának. A nullelem az identitás, aminek megfelelője a nullvektor.

Lineáris altér

Az R³ vektortér néhány altere: két, az origón átmenő sík (sárga és zöld) és metszésvonaluk, egy origón átmenő egyenes (kékkel)

Egy F test feletti V vektortér egy nemüres W ⊆ V részhalmazát altérnek nevezzük V-ben, ha W maga is vektortér ugyanazon F test felett ugyanazokra a V-beli vektorműveletekre, precízebben ezeknek a műveleteknek W-re történő megszorításaira nézve. Jelölése W ≤ V. Mivel W vektortér, azért tartalmazza a nullvektort.

Minden vektortér tartalmazza önmagát és a csak nullvektorból álló vektorteret. Minden altér előáll a másik vektortér képeként úgy, hogy egy lineáris leképezés leképez egy másik vektorteret a tartalmazó vektortérbe; és magtérként is úgy, hogy egy lineáris leképezés leképezi a tartalmazó vektorteret egy másik vektortérbe. Ekvivalenciaosztályok képzésével egy vektortérből és alteréből hányadostér, más néven vektortér állítható elő; ami összefügg az altérnek azzal a tulajdonságával, hogy előáll képként, lásd homomorfizmustétel.

Lineáris leképezések

A lineáris leképezések egy vektorteret egy másikba képeznek a struktúra megtartásával. Az univerzális algebra szerint homomorfizmusok a vektorterek között. Egy ugyanazon $K$ test fölött definiált $U$ vektorteret $V$ vektortérbe vivő $f\colon U\to V$ függvény lineáris leképezés, ha minden $a,b\in U$ és minden $\lambda \in K$ esetén:

• $f(a+b)=f(a)+f(b)$
• $f(\lambda a)=\lambda f(a)$

Ekkor $f$ kompatibilis a struktúrákkal, amelyek a vektorteret felépítik: az összeadással és a skalárral szorzással. Két vektortér izomorf, ha van köztük bijektív lineáris leképezés, vagyis van inverz függvény. Ez az inverz függvény automatikusan lineáris. Az izomorf vektorterek nem különböznek egymástól struktúrájukban.

Lineáris kombináció

V vektortér v₁, v₂, …, v_k tetszőleges vektorai és λ₁, λ₂, …, λ_k ∈ F skalárok.
Ekkor a $\lambda _{1}\mathbf {v} _{1}+\ldots +\lambda _{k}\mathbf {v} _{k}$ ∈ V vektort a v_i vektorok, λ_i skalárokkal képzett lineáris kombinációjának nevezzük.

Lineáris függetlenség

Egy V vektortér véges sok vektoráról akkor mondjuk, hogy lineárisan függetlenek, ha lineáris kombinációjuk csak úgy lehet a nullvektor, ha mindegyik skalár szükségképpen 0. Végtelen sok vektor lineáris függetlenségén azt értjük, hogy közülük bármely véges sok lineárisan független. A v₁,…,v_n ∈ V vektorok lineárisan összefüggőek, ha lineárisan nem függetlenek, tehát

$\exists \ \lambda _{1},\ldots ,\lambda _{n}\in \mathbf {F}$

nem mind nulla skalár, azaz közülük legalább egy nem nulla, hogy

$\lambda _{1}\mathbf {v} _{1}+\ldots +\lambda _{n}\mathbf {v} _{n}=\mathbf {0} .$

Lineáris burok

Néhány vektor lineáris burka az a vektorhalmaz, ami előáll a vektorok lineáris kombinációjaként. Ez egy altér, és a legkisebb vektortér, ami a vektorokat tartalmazza.

Bázis

Egy v vektor az R² térben (kékkel) különböző bázisokban kifejezve: az R² standard bázisában: v = xe₁ + ye₂ (feketével), és egy másik, nem ortogonális bázisban: v = f₁ + f₂ (pirossal)

A bázis a lineáris algebrában egy olyan vektorhalmazt jelent, mely vektorainak lineáris kombinációi reprezentálják egy megadott vektortér valamennyi vektorát, valamint e vektorhalmaz semelyik eleme sem fejezhető ki a többi elem lineáris kombinációjával.
Tehát bázison lineárisan független generátorrendszert értünk.

Feltéve a kiválasztási axiómát, a Zorn-lemma biztosítja, hogy minden vektortérnek van bázisa. A Zermelo-Frankel axiómarendszerben ez az állítás ekvivalens a kiválasztási axiómával.

Ha egy vektort kifejezzük egy generátorrendszer elemeinek lineáris kombinációjaként, akkor a lineáris kombinációban szereplő skalárok a vektor koordinátái az adott bázisban. Egy generátorrendszerben a vektortér minden vektora kifejezhető koordinátákkal; azonban, ha a generátorrendszer nem lineárisan független, akkor ez nem egyértelmű; viszont egy bázisban a koordináták már egyértelműek. Ez megkönnyíti a számításokat, mivel a vektorok helyett koordinátavektorok használhatók.

Dimenzió

Ha adott egy V vektortér, akkor minden bázisának elemszáma, számossága ugyanaz. Ez a számosság a V vektortér dimenziója. Ha a vektortérnek nincs véges generátorrendszere, akkor dimenziója végtelen. A 0 tér dimenziója: 0.

Két, azonos test fölötti vektortér akkor és csak akkor izomorf, ha dimenziójuk megegyezik. Ez lehetővé teszi, hogy a vektorterek bázisainak elemei megfeleljenek egymásnak, ami kiterjeszthető lineáris leképezéssé; így a véges vektorterek közötti lineáris leképezések mátrixszal ábrázolhatók.

Vektorterek izomorfizmusa

Definíció

Két vektortér, V₁ és V₂ izomorf egymással, ha létezik egy kölcsönösen egyértelmű, injektív lineáris (homogén) leképezés V₁-ből V₂-re.

Azaz

$V_{1}\cong V_{2}\ \Leftrightarrow \ \varphi :V_{1}\rightarrow V_{2}\$ lineáris leképezés bijektív.

A vektorterek halmazán az izomorfia meghatároz egy osztályozást. Ez az osztályozás a halmazt diszjunkt részhalmazok uniójára bontja fel. Két vektortér akkor és csak akkor kerül ugyanabba az osztályba, ha izomorf.
E reláció reflexív, szimmetrikus és tranzitív, vagyis az izomorfia ekvivalenciareláció.

Magtér, képtér

Ha $\varphi :V\rightarrow W$ tetszőleges lineáris leképezés, akkor a magtér és a képtér

$\mathrm {Ker} \,\varphi =\{\,\mathbf {v} \in V\,|\,\varphi (\mathbf {v} )=0\,\}$

$\mathrm {Im} \,\varphi =\{\mathbf {w} \in W\,|\,\exists \ \mathbf {v} \in V:\ \varphi (\mathbf {v} )=\mathbf {w} \}$

Megjegyzés: a magtér a V, a képtér a W vektortér altere.

Tulajdonságok

Véges dimenziós vektorterek tulajdonságai

• Egy $\varphi :V\rightarrow W$ lineáris leképezés akkor és csak akkor izomorfizmus, ha

$\mathrm {Ker} \,\varphi =\mathbf {0} \ \wedge \ \mathrm {Im} \,\varphi =W$

• Ha V vektortér F felett, valamint

$\mathrm {dim} \,V=n,\ n\in \mathbb {N} ^{+}\Rightarrow V\cong \mathbf {F} ^{n}$

• Ugyanazon F test feletti véges dimenziós vektorterekre fennáll:

$V\cong W\Leftrightarrow \mathrm {dim} \,V=\mathrm {dim} \,W$

Dimenziótétel

A dimenziótétel azt állítja, hogy tetszőleges lineáris leképezés képterében illetve magterében lévő bármely lineáris független generátorrendszer összelemszáma a kiindulási vektortér dimenziójával egyenlő. Formálisan

V₁ és V₂, két tetszőleges, véges dimenziós vektortér ugyanazon F test felett, továbbá $\varphi \$ tetszőleges lineáris leképezés V₁-ből V₂-be. Ekkor

$\mathrm {dim\,Ker} \,\varphi +\mathrm {dim\,Im} \,\varphi =\mathrm {dim} \,V_{1}$

Műveletek vektorterekkel

Homomorfizmus

Az algebrában egy struktúra egy másikra vett leképezése homomorfizmus, ha megtartja az adott struktúrán végezhető műveleteket. Például vektortér esetén ez azt jelenti, hogy a leképezés megőrzi az összeadást és a skalárral szorzást. Legyenek $U$, $V$ vektorterek az $F$ test fölött; ekkor $f\colon U\to V$ homomorfizmus, ha minden $a,b\in U$ és minden $\lambda \in F$ esetén:

• $f(a+b)=f(a)+f(b)$
• $f(\lambda a)=\lambda f(a)$

ami éppen a lineáris leképezés definíciója.

Faktortér

V egy tetszőleges vektortér F felett, és U egy tetszőleges altere V-nek. A

$[\mathbf {v} ]=\mathbf {v} +U=\{\mathbf {v} +\mathbf {u} \,|\,\mathbf {u} \in \,U\}$

halmazok, ahol v befutja az egész vektorteret, diszjunkt részhalmazok uniójára bontják V-t, ugyanis ha
$\mathbf {v} _{1}-\mathbf {v} _{2}\notin U$ akkor $[\mathbf {v} _{1}]$ és $[\mathbf {v} _{2}]$ diszjunkt, ha $\mathbf {v} _{1}-\mathbf {v} _{2}\in U$ akkor $[\mathbf {v} _{1}]=[\mathbf {v} _{2}].$
Definiálunk két műveletet e halmazok körében

$[\mathbf {v} _{1}]+[\mathbf {v} _{2}]=[\mathbf {v} _{1}+\mathbf {v} _{2}]$

$\alpha [\mathbf {v} _{1}]=[\alpha \mathbf {v} _{1}],\ \alpha \in \mathbf {F}$

Az ily módon definiált műveletek egyértelműek, mivel

$[\mathbf {v} ]=[\mathbf {v} ']\ \Leftrightarrow \ \mathbf {v} -\mathbf {v} '=(\mathbf {v} +\mathbf {w} )-(\mathbf {v} '+\mathbf {w} )\in U\ \Leftrightarrow \ [\mathbf {v} +\mathbf {w} ]=[\mathbf {v} '+\mathbf {w} ],$

$\alpha [\mathbf {v} ]=\alpha [\mathbf {v} ']\ \Leftrightarrow \ \alpha (\mathbf {v} -\mathbf {v} ')=\alpha \mathbf {v} -\alpha \mathbf {v} '\in U\ \Leftrightarrow \ [\alpha \mathbf {v} ]=[\alpha \mathbf {v} ']$

Így egy vektorteret kaptunk, melyet a V vektortér U altere szerinti faktorterének nevezünk, vagy röviden a $V/U\$ faktortér, szokás $V\$ hányadosterének is nevezni.
A faktortér elemei a $\ [\mathbf {v} ],\,\mathbf {v} \in V$ vektorhalmazok, az additív egységelem a $\ [\mathbf {0} ]=U.$

Direkt összeg

Ha $V,W$ vektorterek ugyanazon test fölött, akkor direkt összegük az a vektortér, melynek elemei úgy képződnek, hogy az első komponens az első, a második komponens a második vektortér eleme:

$V\oplus W:=\left\{\left(v,w\right)\mid v\in V,w\in W\right\}$

A vektorokat komponensenként adjuk össze és a skalárral szorzást is komponensenként végezzük. A $V\oplus W$ vektortér dimenziója a tagok dimenziójának összege. Az összeg elemeit $(v,w)$ helyett írják úgy is, mint $v+w$. A direkt összeg általánosítható véges és végtelen tagra is; utóbbi esetén csak véges sok tag különbözhet a nullvektortértől.

Direkt szorzat

Ha $V,W$ vektorterek ugyanazon test fölött, akkor direkt szorzatuk az a vektortér, melynek elemei úgy képződnek, hogy az első komponens az első, a második komponens a második vektortér eleme:

$V\times W=\left\{\left(v,w\right)\mid v\in V,w\in W\right\}$.

A vektorokat komponensenként adjuk össze és a skalárral szorzást is komponensenként végezzük. A $V\times W$ vektortér dimenziója a tagok dimenziójának összege. A direkt összeg általánosítható véges és végtelen tényezőre is; utóbbi esetben akár végtelen sok tényező is különbözhet a nullvektortértől.

Tenzorszorzás

A tenzorszorzás univerzális tulajdonságát szemléltető kommutatív diagram

Ha $V,W$ vektorterek ugyanazon test fölött, akkor tenzorszorzatukat

$V\otimes W$

jelöli. A tenzorszorzat elemeinek bilineáris ábrázolása:

$\sum _{i\in I}\sum _{j\in J}a_{ij}(v_{i}\otimes w_{j})$,

ahol az $a_{ij}$ elemek skalárok, $(v_{i})_{i\in I}$ bázis $V$-ben és $(w_{j})_{j\in J}$ bázis $W$-ben. Ha $V$ vagy $W$ végtelen dimenziós, akkor csak véges sok tag különbözhet nullától. Ekkor $V\otimes W$ dimenziója $V$ és $W$ dimenziójának szorzata. A tenzorszorzás is általánosítható több vektortérre.

Vektorterek további struktúrával

$\mathbf {R} ^{2}$ néhány $p$-normához tartozó egységgömb: az 1-es normához tartozó sárgával, a 2-es normához tartozó zölddel és a végtelen normához tartozó pirossal. A halványsága csúcsra állított négyzet azokat a pontokat jelöli, melyek 1-normája 2

A matematika több alkalmazásában, például a geometriában és az analízisben van, hogy nem elegendő a vektortér struktúra, hanem még további struktúrát is feltételezni kell; így biztosítva például normát vagy határérték létezését. Például:

• euklidészi vektorterek: skalárszorzattal ellátott valós vektortér. A prehilbertterek speciális esete.
• normált tér: egy olyan vektortér, amiben a vektoroknak hossza (normája) van. Ez egy nemnegatív szám, amire teljesül a háromszög-egyenlőtlenség.
• prehilberttér: skalárszorzattal ellátott valós vagy komplex vektortér. Egy ilyen térben a vektorok hossza mellett még a vektorok szöge is definiálható. A topologikus vektortér speciális esete.
• topologikus vektortér: topologikus tér fölötti vektortér, ahol a vektorok összeadása és a skalárral szorzás folytonos műveletek.
• unitér vektortér: többnyire komplex vektortér skalárszorzattal ellátva. A prehilberttér speciális esete.

Topologikus vektorterekben kezelhető a konvergencia, a teljesség és az egyenletes konvergencia. A teljes normált terek Banach-terek, a teljes prehilbertterek Hilbert-terek.

Általánosítások

• Ha a teret test helyett gyűrű felett definiáljuk, akkor modulust kapunk. Egyes szerzők csak kommutatív gyűrűk fölött definiálnak modulusokat. A kommutatív gyűrűk fölötti modulusok az Abel-csoport és a vektortér közös általánosításai.
• Egyes szerzők a ferdetestek fölötti modulusokat is vektortérnek nevezik. Kommutativitás hiányában beszélhetünk bal- és jobbvektorterekről. Ez a helyzet összehasonlítható nem kommutatív gyűrűk fölötti modulusokkal. A cikkben megadott definíció ekkor a balvektorterekhez vezet, mivel a skalár a bal oldalon áll. A jobbvektorterek ennek tükörképi párjai, a skalár jobb oldalon jelenik meg. Több alapvető eredmény átvihető ferdetestek fölé, például bázis létezése.
• Ha test helyett féltestet veszünk, akkor félvektorteret kapunk.
• Egy másik általánosítás a vektornyaláb, ami vektorterek egy topologikus tér pontjaival paraméterezett családja.

Történeti megjegyzés

Bartel Leendert van der Waerden megjegyzi, hogy tudomása szerint az n-dimenziós vektortér fogalmát először Hermann Günther Graßmann használta 1844-ben megjelent Die lineale Ausdehnungslehre című könyvében. Implicit már korábban is használták a fogalmat.

Kapcsolódó szócikkek

• Algebra
• Duális tér
• Lineáris algebra
• Lineáris leképezés
• Tenzor
• Tenzorszámítás
• Vektor

Irodalom

• Bronstejn – Szemengyajev – Musiol: Matematikai kézikönyv' (TypoTeX, 2002)
• Dancs I. – Puskás Cs.: Vektorterek (Aula Kiadó, 2003)
• Sain Márton: Matematikatörténeti ABC (Tankönyvkiadó, 1978)
• Scharnitzky Viktor: Mátrixszámítás. Bolyai-könyvek sorozat (Műszaki Könyvkiadó, 1998)
• Surányi László: Algebra, testek, gyűrűk, polinomok (TypoTeX, 2004)
• Szász Gábor: Matematika II. (Nemzeti Tankönyvkiadó, 2000)
• Szendrei János: Algebra és számelmélet (Nemzeti Tankönyvkiadó, 1996)

Források

• Freud Róbert: Lineáris algebra (ELTE Eötvös Kiadó, 2004)
• Fried Ervin: Algebra I., Elemi és lineáris algebra (Nemzeti Tankönyvkiadó, 2000)
• Kuros, A. G.: Felsőbb algebra (Tankönyvkiadó, Bp., 1975)
• Praszolov, V. V.: Lineáris algebra (TypoTeX, 2005)
• Gerd Fischer: Lineare Algebra. Vieweg-Verlag, ISBN 3-528-03217-0.
• R. Hartwig: Syntax, Semantik, Spezifikation - Grundlagen der Informatik Archiválva 2022. december 21-i dátummal a Wayback Machine-ben. WS 2009/2010.

Fordítás

Ez a szócikk részben vagy egészben a Vektorraum című német Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.

További információk

• Encyclopedia Of Maths: Linear operator (angolul)
• MathWorld: Linear algebra (angolul)
• MathWorld: Linear transformation (angolul)
• PlanetMath: Linear algebra Archiválva 2012. június 12-i dátummal a Wayback Machine-ben (angolul)
• PlanetMath: Linear transformation Archiválva 2007. szeptember 30-i dátummal a Wayback Machine-ben (angolul)
• Wikipedia: Algebra (angolul)
• Wikipedia: Euclidean space (angolul)
• Wikipedia: Linear Map (angolul)
• Wikipedia: Linear algebra (angolul)
• Wikipedia: Normed vector space (angolul)
• Wikipedia: Topological vector space (angolul)