Fraktál
A fraktálok végtelenül komplex geometriai alakzatok, amelyek két gyakori, jellemző tulajdonsággal rendelkeznek. Az első, hogy a tradicionálisan a geometria által vizsgált, bizonyos értelemben véve „egyszerűbb” és „szabályosabb”, „simább” alakzatokkal ellentétben (mint pl. egy töröttvonalakkal határolt sokszög, vagy egy görbével határolt ellipszis), a fraktálok határoló vonalai vagy -felületei végtelenül „gyűröttek” vagy „érdesek”, illetve „szakadásosak” (szakkifejezéssel, nem-differenciálhatóak).[mj 1] A második gyakori jellemzőjük a rendkívül problematikus, de „laikus szemmel” is jól érzékelhető önhasonlóság.



Bevezetés[szerkesztés]
Egy sokszög, egy kör, vagy egy gömb határfelületét egyre nagyobb nagyításban szemlélve azt tapasztaljuk, hogy a határfelület – elszigetelt pontokat, pl. a sokszög csúcsait kivéve – „kisimul”, bizonyos nagyításban már megkülönböztethetetlenné válik – síkgörbénél – az egyenestől, vagy – testnél – a síktól. A fraktálokat ezzel szemben bármilyen nagy nagyításban is vizsgálva, mindig találunk „gyűrődést” vagy „szakadást”, matematikai szemszögből, olyan részeket, melyeknek nem állandó, vagy nem is létezik a differenciálhányadosa. A „hagyományos” és „szabályos” geometriai alakzatok pontjainak nagy része tehát az alakzat „sima” pontja, és csak véges sok, a pontok végtelen összességéhez képest elenyészően kevés „töréspont” vagy „csúcspont” van.

A fraktálalakzatok esetében viszont pont fordítva van: éppenséggel a „töréspontok” közönségesek, legalábbis az alakzat bizonyos helyein nagyon sok található belőlük; míg a „sima” felületeket adó (differenciálható) pontok a kivételesek. Míg a pontbeli differenciálhatatlanság a „hagyományos” alakzatok esetében csak egyes elszigetelt pontok kiugró jellemzője, a fraktálok esetében éppen ezek a jellemzőek a közönségesek; melyek megadják a görbe lényegi jellegét. Benoit B. Mandelbrot, a fogalom névadója[2] szavai nyomán: „a fraktálok geometriája a skálafüggetlen (akárhányszoros nagyítás után is megmaradó) egyenetlenség tudománya.[3]
Ezeknek a fraktálalakzatoknak valamelyik, vagy nagyon sok kiragadott, nagyobb vagy kisebb nagyításban látható részletei ráadásul sok esetben (a matematikai szigorúságnál jóval megengedőbb értelemben) „hasonlítanak” a teljes alakzatra vagy annak más részeire (önhasonlóság).



A végtelenül sűrűn (akárhányszoros „mikroszkóp”-nagyításban is fellelhető) „egyenetlenség” (differenciálhatatlanság) sok kellemetlennek vagy szokatlannak is értékelhető matematikai következménnnyel jár (ld. a Cantor-Lebesque-görbéről szóló illusztrációhoz mellékelt képaláírást). A legdurvább következmény ezek közül a fraktálok másik fontos tulajdonsága: az olyan geometriai jellemzőik, mint a kerület, terület, térfogat, ívhossz, felszín, sőt: a térdimenzió, elfajult (végtelen vagy nulla) értékeket adnak, és általában is, a térszemlélettel ellentétesen, meglepő és paradox módon viselkednek. Pongyolán fogalmazva, ezek az alakzatok nehezen, az iskolás, sőt az egyetemi geometriakönyvekben is szereplő, évszázadok óta bevált matematikai módszerekkel nem mérhetőek. Innen nyerték nevüket is: a latin fractus melléknév, a frangere, „törni” ige származéka, ugyanis elsősorban töröttet, darabosat (vö. „mindenütt tüskésség” vagy „mindenütt szakadásosság”), másodsorban szabálytalant, kivételest jelent. Mandelbrot ebből a latin szóból alkotta meg a fraktál kifejezést. A fraktálok jelentőségét a matematikán belül főleg ez a szabálytalan, „kényelmetlen” jelleg adja – matematikai leírásuk új eszközöket igényel (ezek leginkább a topológia, azon belül a mértékelmélet és a metrikus terek elméletének körébe tartoznak) és olyan problémákat vet fel, melyeket ma már nem bosszantónak és riasztónak tartanak, mint egykor, hanem lebilincselőnek. Azonban a fraktálok jelentősége a matematikán kívül is óriási.
A fraktálok diadalmenetének története tele van váratlan felfedezésekkel és más tudományos szenzációkkal, valamint könnyen érthetővé tehető és jelentőségteljes problémákkal, így hálás témát jelent a népszerűsítő irodalom számára. Fraktálokat – legalábbis ami a tudományos vizsgálatukat illeti – először a XIX. század végén fedeztek fel matematikusok a valós analízis és topológia halmazelméleti megalapozására irányuló vizsgálatainak (nem kívánt) eredményeképpen, bár ekkor még nem nyertek önálló elnevezést, és évtizedekig tudatos, rendszeres vizsgálatuk sem kezdődött meg; viszont a XX. század második felében (nem várt módon) előbukkantak különféle műszaki, fizikai, kémiai, élő, s végül kozmológiai rendszerek viselkedésének matematikai leírásának vizsgálatakor is. A XX. században a dinamikai rendszerek fizikája révén – összefüggésben ennek egyik legjelentősebb felfedezésével, a determinisztikus káosz fogalmával – elindult a fraktálok diadalútja a közismertség és népszerűség felé: kiderült, hogy a fraktálok geometriája a természet és a társadalom számos, akár mindennapi, akár extrém jelenségének leírásában (itt a fizika mellett a kozmológia, a közgazdaságtan, a komputergrafika, a rákgyógyászat és még tucatnyi más kiemelt fontosságú terület is érdekelt) a kulcsot jelentheti, fogalmak és elméletek olyan gazdagságát és olyan magyarázó erőt, ami jóval meghaladja a „hagyományos” geometria teljesítőképességét.
A fraktál fogalmának nincs a tudományos (matematikai, elméleti fizikai) szakirodalomban általánosan elfogadott, szigorú definíciója: maga a definíció is kutatási területet jelent. Érdekesség, hogy Mandelbrot tudatosan kiterjesztette a fogalom jelentését a geometriai alakzatok mellett a természeti jelenségekre is. Eszerint egy matematikai értelemben véve fraktálszerűnek kinéző természeti képződményre vagy mintázatra – például egy levélerezetre vagy egy nagyváros metróvonal-hálózatára – is mondhatjuk, hogy az fraktál.
A definíció problematikája[szerkesztés]
A fraktálok matematikai definíciójáról egyelőre nincs végleges megállapodás a szakirodalomban.[4] Több lehetséges matematikai út is kínálkozik (ezek közül két-három alapelgondolás lépte túl a vitairat-szintet), azonban egyik sem fedi le teljes egészében az összes olyan példát, amiket a különféle területeken dolgozó szakemberek is fraktálnak tartanak, de nem is zárják ki az összes olyan fogalmat, amik fraktálként való tanulmányozása nem bír érdekességgel.
Az eredeti és talán legszélesebb körben elfogadott definíciót, miszerint fraktálnak nevezünk egy geometriai alakzatot akkor, ha „induktív” (vagy „topológiai”) dimenziója szigorúan kisebb a Hausdorff-féle dimenziójánál, elgondolásainak változása eredményeképp a fogalom keresztapja, maga Mandelbrot elvetette (minden más általa ismert definícióval együtt).[4] Ez a definíció különben sem illik az olyan, kétségkívül és szigorú értelemben önhasonló, és széles körben fraktálisnak tartott görbékre, mint a XIX. század végén felfedezett Peano-görbe.
Bár negatív jellegű, és nem minden szerző ennyire szkeptikus a kérdésben, mégis szükségesnek tűnik idézni Mandelbrot véleményét „Gauss-féle önaffinitás és a fraktálok”[5] c. könyvéből (2002), a fraktálok fogalmának és tudományának definíciós problémájáról: „Könyvem 2. fejezetében amellett érvelek, hogy informális jellegű szavaim – ti., hogy a fraktálgeometria a skálafüggetlen durvaság tudománya – valószínűleg a legjobb jellemzés, aminek elérésében a fraktálgeometria reménykedhet; megfelelőbb szigorú definíció nem létezik, és megalkotása nem is várható (el).” (9. old.); „... későbbi bánatomra, 1977-es és 1982-es könyveimben felcseréltem a fraktál igen általános, nyitott fogalmát, közreadva egy – úgymond – taktikai definíciót, két fontos és jól definiált, ámde szűken mérő fogalom: a topológiai és a Hausdorff-Beszikovics-féle dimenzió közti irregularitással. Ez az út azonban szándékolatlan és szerencsétlen következményeket eredményezett, úgyhogy azóta feladtam. Például kizárta a fraktálok közül az ördög lépcsőjét, mely alakzat esetében mindkét érték 1. Hogy ezt a fraktáltalanítástól megmentsem, később megkíséreltem a fraktálságot az önhasonlóságra és önaffinitásra visszavezetni, de – amint a 2. fejezetben megmutatom – ez utóbbi elgondolás is túl ellentmondásos ahhoz, hogy szilárd alapul szolgálhasson. Összefoglalva, úgy gondolom, hogy az olyan kérdésekre, mint hogy mik a fraktálok és multifraktálok, mi az önhasonlóság és önaffinitás, vagy a globalitás, és más egyebekre ebben a könyvben talán sohasem kaphatunk precíz matematikai választ. Akár elegendően hasznosnak bizonyul majd a fraktálgeometria, hogy fennmaradjon, akár nem, úgy gondolom, az effajta terminológiai kérdések el fognak felejtődni.” (i.m., 18. old.)
Egy másik út, a műszaki tudományokból és a dinamikai rendszerek elméletéből eredő elgondoláscsoport, amely szerint a fraktálok fogalmát a kaotikus rendszerek fázistereinek ábrázolásakor kapott különös attraktoraiból vezetjük le, olyan fogalomhoz vezet, amely alá egyszerű megformulázhatóságuk ellenére végtelenül komplex és „divergens” viselkedésű ábrák is tartoznak, megfelelően a fraktálokról való elképzeléseknek; ámde ezek egy része csak valamiféle nehezen megfogható, vagy statisztikus értelemben önhasonló (különösen igaz ez a már matematikai leírásukból következően statisztikus jellegű rendszerekre, mint pl. egy Brown-mozgást végző részecske). A „fraktálszerű” fizikai/kémiai (sőt, kozmológiai) rendszerekre részlegesen (bizonyos léptékhatárokig) jellemző lehet az ún. skálafüggetlenség (amely lényegében a geometriai önhasonlóság fizikai analogonja), illetve a determinisztikusság ellenére véletlenszerűhöz hasonló (vagyis kaotikus) viselkedés, ugyanakkor a szakirodalom egyik tulajdonságot sem fogadta el egységesen, mint a „fraktális leíráshoz vezető rendszer” fogalmának általános definícióját.
A fraktál fogalmát – főleg a laikusok körében – igen gyakran azonosítják az önhasonlóság fogalmával. Ez szemléletesen kétségkívül könnyen megfogható és a gyakorlatban azonosításra használható tulajdonsága a fraktális jellegnek, a matematikai definiálás számára azonban – több egyéb, kisebb probléma mellett – azért nem jelent használható lehetőséget, mivel képtelenségnek látszik szigorúan definiálni úgy, hogy az megfeleljen a szemléletből következő elvárásoknak.
Kisebb problémának minősül, hogy bizonyos alakzatokat, amelyeket általában nem tartunk fraktálnak, az önhasonlósági karakterizáció alapján fraktálnak kellene minősíteni. Ilyen egyszerű példa bármilyen teljes (lyukak nélküli) egyenesszakasz, egy zárt körlemez, és a geometria hagyományos, jól viselkedő alakzatai közül még rengeteg olyan, amiktől a „fraktálgeometria” épp hogy „elhatárolódni” igyekszik, hiszen pont a nem ilyen alakzatok vizsgálatát tűzte ki célul. Bár akadnak szerzők, akik amellett érvelnek, hogy értelmes dolog egy egyenes szakaszt is fraktálnak tekinteni, a most elmondottak értelmében nehezen látható, hogy ebből mifajta előny származna a már amúgy is kérdéses fogalmaknak még az eddiginél is elmosódottabbá tételén túl.[6]
Még nagyobb probléma, hogy a kínálkozó egzakt önhasonlósági definíciók (és változataik) túlságosan szigorúak: a hasonlósági transzformáció a matematikában egy nagyon partikuláris fogalom, a legtöbb fraktál önhasonlósága azonban csak közelítő, szemléletes jellegű, de nem állná ki a matematikai fogalmak szigorú megkötéseit. Egy „többé-kevésbé” önhasonló Mandelbrot-halmaz pl. egészen másféle értelemben önhasonló, mint egy ténylegesen önhasonló Cantor-szőnyeg, vagy egy (statisztikus jellege ellenére szigorú értelemben is önhasonló) Wiener-folyamat; sok statisztikus fraktál (mint pl. egy valóságos, matematikai idealizációtól mentes Brown-mozgás pályagörbéje, vagy egy DLA-szimulációs ábra) pedig szinte csak valamilyen metaforikus értelemben mutat geometriai önhasonlóságot. Ez a megállapítás vonatkozik e definíciókísérlet kézenfekvőnek tűnő általánosítási kísérleteire is,[7] amelyek egy nagyobb, de szintén determinisztikusan kiszámítható transzformációcsaláddal szembeni invarianciát (önaffinitást vagy önkonformitást) várnak el a fraktáloktól.
Történeti áttekintés[szerkesztés]
Felfedezésük[szerkesztés]
A szigorúság forradalma[szerkesztés]
- Fő szócikk: A szigorúság forradalma

Az első fraktálokat az 1800-as évek utolsó évtizedeiben fedezték fel, ám ekkoriban még nem nyertek önálló „szaktudományos” elnevezést, inkább kellemetlenségnek és vitaalapnak számítottak a matematikusok számára, minthogy divergens viselkedésük miatt a függvénytan akkori eszköztára számára kivételes, az intuíciónak ellentmondó eseteket, problémát és kihívást jelentettek. A fraktálszerű alakzatok elfajult esetként, a józan geometriai intuíciót megcsúfoló ellenpéldákként kezdték matematikán belüli pályafutásukat: megdöntötték azt a tévhitet, hogy különféle topológiai vonatkozású problémák, például a térdimenzióké, a görbék simaságáé, folytonosságáé és integrálhatóságáé triviálisak, az analízis akkori eszközeivel (differenciál- és integrálszámítás) könnyen átláthatóak és lezárhatóak lennének. A szigorúság forradalma – a matematikusok egyre erősebb törekvése arra, hogy sejtéseiket és elvárásaikat szilárd alapra építsék – félsikernek bizonyult: a matematika alapjai valóban sok tekintetben átláthatóbbá és bizonyosabbá váltak, ám rengeteg remény, elvárás és előítélet, amelyek központi jellegű tételek igazságát vélték az új módszerekkel rövid úton bebizonyítani, csalókának bizonyult. Számos nagyon fontos és/vagy befutóvárományos tétel inkább cáfolatot nyert, ahelyett, hogy általános érvényűnek bizonyult volna.
Weierstrass és Volterra függvényei[szerkesztés]
Az elsőként felfedezett és publikált függvénytani szörnyeteg Karl Weierstrass dupla vé formájú görbéje volt, aki 1872-ben a Berlini Akadémián tartott előadásában mutatta be (valójában már Bernard Bolzano is felfedezett egy majdnem ugyanolyan görbét 1830 körül, de nem publikálta, és csak az 1930-as években került elő).[8] A Weierstrass-görbe megdöntötte azt a széles körben uralkodó tévhitet, vagy inkább elvárást, hogy egy folytonos görbének izolált pontokat leszámítva mindenütt simának (differenciálhatónak) kell lennie; Weierstrass görbéje bár folytonos, ám nemhogy egy számottevő szakaszon nem sima, hanem semelyik pontjában sem: „mindenütt tüskés”. Bár, amint a későbbi példák megmutatták, szemléletesen könnyen konstruálhatóak ilyen görbék, azonban Weierstrassnak a „hagyományos”, folytonos analízis jól ismert alapelemeiből, elemi – mégpedig folytonos, trigonometrikus – függvényekből sikerült egy ilyen, viszonylag egyszerű képlettel megadható függvényt konstruálnia, és nem kellett ehhez új fogalmakat, vagy műveleteket bevezetnie.
A megdöntött tételek között volt még az infinitezimális kalkulus legfontosabb tétele, a Newton–Leibniz-tétel is (más néven az integrálszámítás alaptétele) – pontosabban annak naiv, minden függvényre alkalmazhatóságot állító formája – ami a függvénytan két alapoperációja, a deriválás és integrálás egymáshoz képest fordított művelet voltát mondja ki, és teszi ezáltal lehetővé Newton ideje óta az egész, differenciálegyenletekre épülő fizikát és műszaki tudományokat. E tétel korlátozott voltát Vito Volterra olasz matematikus ismerte fel, aki felfedezte a ma Cantor-Volterra-Smith-halmazként ismert fraktálalakzatot, és erre épülve megalkotta a Volterra-típusú függvények családját. A Volterra-függvény valós függvény, amely minden pontjában deriválható, és deriváltja ráadásul korlátos, azonban – egy jól viselkedő függvénytől elvárható móddal ellentétben – a derivált integrálásával nem kapjuk vissza az eredeti függvényt, mivel a derivált nem is integrálható.
„Reakció”[szerkesztés]

Az analízis és a fizikában való, a köztudat szerint Newtontól (valójában Arkhimédesztől és Galileitől) induló alkalmazásának első, világképformáló sikerei nyomán a tudományos világban is kialakult derűlátás után a negatív eredmények csalódást, sőt riadalmat keltettek. Ilyen körülmények között talán érthető volt számos régivágásúbb matematikus reakciója az új, tételgyilkos halmazokra és görbékre. Bár a szaktudományos terminológia a jelenség újdonsága miatt hiányzott, gyakran alkalmazott, noha inkább gúnyos jelzőjük, gyűjtőnevük éppenséggel akadt. Mindegyik Henri Poincarétől, a korszak egyik nagy tekintélyű matematikusától származott, aki részben szörnyetegeknek, részben pedig patologikusnak (betegesnek)[9] és teratologikusnak (≈ nyomoréknak, torzszülöttnek) nevezte őket. Poincaré e szavait 1899-re datálják, írásban is megjelentek (Tudomány és módszer c. könyvében) 1908-ban:
|
A szörnyetegekről kiderül, hogy tipikusak[szerkesztés]
Egy szintén korán felfedezett, de Weierstrass és Volterra alakzatainál jóval többet vizsgált és idézett korai szörnyetegalakzat a Georg Cantor által elsőként leírt Cantor-halmaz volt (1883), amely később Benoit Mandelbrotot egyik inspirálója lett a fraktál fogalmának megalkotásakor. A Cantor-halmaz valójában a Volterra-halmaz speciális, jóval egyszerűbb esete, ennek ellenére tudománytörténetileg külön utat járt be. Cantor nem a differenciálhatóságot, hanem a ponthalmazok mérhetőségét vizsgálta, ennek során ellenpéldaként alkotta meg alakzatát arra a (hamis) állításra, miszerint egy perfekt, izolált pontokkal nem rendelkező alakzat mindenütt sűrű (a Cantor-halmaz sehol sem sűrű). A Cantor-halmaz számos más érdekes tulajdonsággal rendelkezik, és elég egyszerű a leírása, így afféle állatorvosi ló a topológiában, a valós függvénytanban és a mértékelméletben, mint számos kézenfekvőnek tűnő állítás ellenpéldája.
A következő évtizedekben és a huszadik század elején további különös görbék és halmazok születtek, mint pl. a Cantor-Lebesgue-görbe, köztük sokkal könnyebben átlátható konstrukciójú alakzatok is voltak, pl. Koch hópelyhe, ill. a Peano-görbe, melyek még alapvetőbb, térrel kapcsolatos intuíciókat (pl. hogy egydimenziós görbével nem lehet kétdimenziós teret hézagmentesen kitölteni) döntöttek meg. Mindazonáltal egyre kevésbé tekintették nemkívánatosnak őket, és ez részben szintén Cantor érdeme, aki megalkotta a nemsokára az egész matematika alapjává vált halmazelméletet. Ez lehetővé tette a végtelen halmazok elemszámának megkülönböztetését, és olyan további tudományágak megszületését, mint a halmazelméleti topológia és a mértékelmélet. Ezáltal nemcsak jóval könnyebbé vált a tételek cáfolatát megadó szörnyetegek és ellenpéldák gyártása, de a függvényterek és más halmazelméleti konstrukciók egymáshoz viszonyított elemszámával való szembesülés is. Ennek során az is kiderült, hogy az addig ismert szabályos, sima és folytonos halmazok, függvények és görbék csupán csekély számú speciális esetet jelentenek: a szakadásokkal teli és egyéb okokból megmérhetetlen szörnyetegek a legtöbb mérési és kategorizálási koncepciót alkalmazva (mint pl. a Baire-kategóriák) jóval tipikusabb lakói a valós számok által képviselt kontinuumra épülő geometriai univerzumnak. Mindazonáltal a matematikusokon kívül nem sokan ismerték vagy alkalmazták őket.
A komplex függvénytanban és fizikai rendszerelméletben elért eredmények[szerkesztés]
Az analízis tudománya a mértékelmélet, a metrikus terek elmélete, az absztrakt topológia, és más ágak létrehozásával jelentős fejlődésen ment keresztül, és ez nem kis részben a szörnyszülött-alakzatoknak volt köszönhető. Olyan, addig irreguláris (divergens, sehol sem differenciálható stb.) viselkedésűnek tekintett alakzatok vizsgálata is lehetővé téve, amilyenek a többdimenziós differenciálgeometriában/differenciáltopológiában fellépő szingularitáselméleti jelenségek. Az 1910-es évek végén a komplex függvénytan / rendszerdinamika terén elért eredmény, a Julia- és Fatou-halmazok felfedezése és tanulmányozása, újabb fraktálokkal gazdagította a tudományt. Ezek jóval gazdagabb, változatosabb, kevésbé szabályos mértani struktúrák voltak, mint a halmazelméletesek és a geometriai topológusok által konstruált addigi példagörbék és példasíkidomok; azonkívül bizonyos értelemben jóval természetesebbek is, minthogy ismeretlenségük ellenére az alkalmazott matematikához jóval közelebb eső problémákból származtak. Az elmélet nehézsége és mélysége azonban nem tette lehetővé, hogy a felfedezés bekerüljön a populáris kultúrába.
A káoszelmélet kialakulása, amely a fraktálképekkel kölcsönhatásban bizonyos népszerűségre és közérdeklődésre tett szert; szélesebb körben világossá tette, hogy a hagyományos geometriai alakzatok nem elegendőek minden, a műszaki életből vett probléma leírása. Számos rendkívül érdekesen viselkedő rendszer (elsősorban a nemlineáris állapotleíró függvényekkel rendelkezőek) leírása önhasonló, vagy végtelenül komplex, fraktálszerű ábrákhoz vezet, olyanokhoz, amelyeket a múlt századi matematikusok még bosszantó kellemetlenségnek, esztétikátlan szabálytalanságnak tartottak. Ehhez nem szükségesek bonyolult formulák: már a legegyszerűbb másodfokú állapotleíró függvényekkel adott rendszerekben is megjelenhet a kaotikus viselkedés.
A „fraktál” kifejezés születése[szerkesztés]
A végső lökést a népszerűség irányába 1975-ben adta Benoît Mandelbrot amerikai matematikus, aki nemcsak mélyreható vizsgálatokat végzett a fraktálokkal kapcsolatban, de tudatos népszerűsítést is. A fraktál szót a latin fractus (vagyis törött; törés) szó alapján alkotta meg; ami az ilyen alakzatok tört értékű dimenziójára utal, bár nem minden fraktál törtdimenziós (ilyenek például a síkkitöltő görbék). Ő hívta fel a témáról írt értekezéseiben és könyveiben (pl. a Nagy-Britannia partvonalának hosszáról írtban, amelyben a fraktál szót még nem használta) arra is a figyelmet, hogy számos egyszerű, köznapi természeti alakzat viselkedik bizonyos mértékig fraktálként.
Mandelbrot matematikából doktorált, majd egy francia tudományos intézetben helyezkedett el, ahová azonban nem érezte odaillőnek magát, ezért otthagyta. Mandelbrot, akinek iskolai képzése a II. világháború miatt félbemaradt (szülei menekültek a nácik elől), afféle csendes lázadó és nonkonformista volt. Nem szerette a modern matematikának a szigorúság forradalma meg a Bourbaki-csoport által kialakított stílusát, az ábrák és vég nélkül való, szemléltetés nélküli képlethalmazokat, azt a matematikát szerette, ami látható, megjeleníthető. Vizuális típus volt, aki képekben szeretett gondolkodni.[11]
Ezután, 1958-ban, az IBM Thomas J. Watson Kutatóközpontjának laboratóriumába került, ahol többek között a számítógépek kutatásával és fejlesztésével foglalkoztak. Mandelbrot feladata azonban nem ez volt. Az IBM kirendeltségei telefonvonalakon kommunikáltak egymással, azonban a küldött üzenetek időnként akkora csatornazajnak voltak kitéve, hogy használhatatlanná váltak. Az IBM azt szerette volna, ha egy matematikus is dolgozik azon, hogyan lehetne ezt a zajt csökkenteni, vagy legalábbis az adatokat visszanyerhetően szállítani. Mandelbrot megvizsgálta a zajos adatokról készült grafikus naplókat, és olyan felfedezést tett, ami komolyan meglepte: a zaj alapszerkezete skálafüggetlennek mutatkozott. Akárhogy is kicsinyítette le az időintervallumot, amin vizsgálta a jeleket (azaz akárhogy is nagyította a grafikonokat), ugyanannak a vonalas szerkezetnek a változatai tűntek fel előtte.[12][13]
Ehhez hasonló jelenséggel már szembesült tanulmányai során, ugyanis egyetemi tanulmányai alatt a Brown-mozgással foglalkozó Paul Lévy és a differenciáltopológia Fatou-halmazaival foglalkozó Gaston Julia tanítványa volt. Hamar kialakult benne a sejtés, hogy a Julia által vizsgált alakzatok ugyanolyan fraktálszerkezettel bírnak, mint a vizsgált zajdiagramok, illetve ezek kínálkozó matematikai modellje, a Cantor-halmaz. Így aztán természetes módon elkezdte tanulmányozni a századforduló furcsa szörnyetegalakzatait is. Rá kellett jönnie, hogy ezek a „szörnyetegek” egyáltalán nem furák és rendkívüliek, hanem teljesen alapvetőek és közönségesek: ha valami természetellenesnek minősíthető, valójában leginkább az évezredek óta használt geometria szép és szabályos, majdnem mindenütt differenciálható alakzatai és görbéi azok. Szállóigévé vált megállapítása szerint: „A felhők nem gömbök, a hegyek nem kúpok, a partvonalak nem körívek, a fakéreg nem sima, és a villám sem terjed egyenes vonalban.”
Ám Mandelbrotnak megvolt a saját kedvenc fraktálja, az a komplex síkalakzat, amit később róla neveztek el: a Mandelbrot-halmaz. Kutatásai során egy térképet szeretett volna készíteni, ami a maga jellegzetes matematikai módján az összes Julia-halmazt tartalmazta. A Mandelbrot halmaz szerkezetének mélyebb megértése azonban csak akkor kezdődött el, amikor sikerült számítógéppel megfelelő minőségű ábrát rajzolni róla.
Ez csak részben Mandelbrot érdeme, mégis később azt állította, hogy a Mandelbrot-halmazt egyedül fedezte fel. Kijelentéséből ízetlen nyilatkozatháború alakult ki arról, hogy kinek a felfedezése is valójában a Mandelbrot-halmaz. Az odamondogatásokból álló párbajban Mandelbrot ellenfelei sem kívánták tőle a felfedezést teljes egészében elvitatni, azonban kifogásolták, hogy másokat teljesen kirekeszt még a lábjegyzetben való megemlítésből is. A rosszmájúbb vélemények szerint Mandelbrot végül is alig fedezett fel valamit, a Mandelbrot-halmaz lényegében már Julia cikkeiben feltűnik. A még rosszmájúbbak azt is állították, hogy maga Gaston Julia sem fedezett fel semmi újat, hanem Fatou-halmazokkal foglalkozott, de meggyőzte a matematikusközösséget arról, hogy Fatou hozzájárulása jelentéktelen volt a témához. Még olyan vélemény is napvilágot látott, amely szerint a Mandelbrot-halmazt végül is már Riesz Frigyes magyar matematikus is felfedezte a század elején.[14][mj 6]
Mandelbrot és a „fraktálgeometria”[szerkesztés]
Mandelbrot egy új szót is alkotott, a „fraktálgeometriát”, és ezzel a prioritásvitán felül még más gond is akadt, ugyanis magára vonta a szigorúbb, a tudományos sztenderdek felrúgása iránt kevésbé megbocsátó, „szakbarbárabb” matematikusok rosszallását.
Krantz cikke[szerkesztés]
1989 végén jelent meg Steven G. Krantz cikke – Fractal Geometry; azaz „Fraktálgeometria” – a Mathematical Intelligencer (Matematikai Hírszerző) c., a matematika kultúrájával foglalkozó folyóiratban;[15] a benne foglaltak támadó jellege miatti elfogadási huzavona miatt később, mint szerzője tervezte (és máshol).[mj 7] Krantz, egy többváltozós függvényekkel foglalkozó analista és fiatal egyetemi professzor, közismertté lett vitairatában igen éles szavakkal Mandelbrotot és az ún. fraktálgeometriát bírálta. Annak elismerésével, hogy a fraktálnak, mint fogalomnak, lehet bizonyos értelme, gyakorlati jelentősége – lényegében kétségbe vonta Mandelbrot tudós voltát, valamint a „fraktálgeometria” tudomány voltát. Krantz szerint Mandelbrot kifejezetten jó abban, hogy „csinos kérdéseket álmodjon meg” – azonban lényegi tudományos munkát sohasem végzett. A matematika ugyanis egy terület összefüggéseit, alapproblémáit világossá tevő fogalmak megalkotásából és az ezekre vonatkozó tételek bizonyításából áll – a „fraktálgeometria” azonban nem ilyen. Egyetlen matematikailag megfogható fogalma, a „hasonlósági dimenzió” (Krantz gondolatai a nyolcvanas évek végének állapotát írják le), mindössze a jóval bonyolultabb Hausdorff-dimenzió egyfajta szellemszerűvé, közérthetővé degradálódott változata; a fraktálgeometriai „tételek” pedig újra és újra ugyanannak a pár alapgondolatnak a szajkózásai: „nini, felnagyítok egy részt, hát nem ugyanolyan, mint az egész”? A matematikai tételek valahol mégiscsak a valóságról szólnak, ha nem is közvetlenül alkalmazhatóak, mindenesetre ilyen fogalmakból keletkeznek – a fraktálgeometriai „kutatás” azonban puszta köldöknézés. Ez nem azt jelenti, hogy az egyes fraktálok semmire sem jók, de vizsgálatuk ennek ellenére nem komoly matematika. A „fraktálnépség” (fractal people), ahogy Krantz Mandelbrot követőit és „rajongóit” nevezte, nem bizonyít tételeket, hanem idejét alakzatok rajzolásával és kinézetének elemzésével tölti.
Krantz hangsúlyozta azt is, hogy nem a fraktál mint újdonság matematikai alkalmazásai – mint pl. a Hausdorff-dimenzió vagy a nemrektifikálható görbék elmélete ellen van kifogása, hanem Mandelbrot könyveinek zavarossága és az ennek ellenére tett nagyhangú kijelentései ellen, amik összekeverik a prematematikát a matematikával. Még csak azt sem várja el, hogy a Mandelbrot könyveiben lévő „fraktálgeometria” tétel-bizonyítás-tétel-bizonyítás rendszerű szakcikkek gyűjteményévé váljon; azonban még az informális alapfogalmak rendszerezése és az alapállítások megsejtése sem történt meg ezekben, csak olyan megállapításokat olvashatunk, hogy „úgy tűnik, ezt a kutyafej-fraktált a természet nagyon szereti alkalmazni”; az ilyesmi még filozófiának is gyenge. Nem zárható ki, hogy a fraktálok elmélete 300 év múlva talán ugyanolyan fontossá válik, mint ma az analitikus függvénytan, és az sem tagadható, hogy Mandelbrot könyvei élvezetes invitálást jelentenek erre a fiatal területre. A körülötte csapott szenzációhajhászás, „tudományoskodás”, és önreklám, ami erősen kifogásolható.
Krantz megismételte azt a más matematikusok által is vallott véleményt, hogy a Mandelbrot-halmazt egyáltalán nem Mandelbrot fedezte fel, hanem Fatou és Julia. Kifejtette abbeli véleményét is, hogy a fraktálgeometria szektásai veszélyt jelentenek a komoly matematikára: könnyen meggyőzhetik a tudatlan politikusokat, hogy a matematikai intézetek fenntartása helyett vásároljanaka inkább pár számítógépet, és futassanak rajtuk heurisztikus elemzéseket; „rendkívül nyomasztó belegondolni, hogy egy ilyen intézkedésnek miféle hosszútávú hatásai lehetnek.” A fraktálnépség azt állítja, hogy a természetleírás új tudományának nyelvét teremtik meg, valójában minden olyan fraktálelméleti felfedezés, ami ténylegesen ebbe az irányba mutat, teljességgel esetlegesnek tűnik: „vagyis, röviden, a császár meztelen”.[16]
„A fraktálgeometria”[szerkesztés]
Annyi bizonyos, hogy a gyakori és túlzó vélekedéssel ellentétben a „fraktálgeometria” nem igazán jelent önálló, elkülönült tudományágat a matematikán, de semmiképpen sem a geometrián belül – legalábbis évtizedekig semmiképp nem volt ilyennek tekinthető. Sokkal inkább egy prototudománnyá is csak lassacskán fejlődött multidiszciplináris ismeretterület, ahová elméleti és alkalmazott ismereteket egyaránt sorolnak, maga Mandelbrot is – különös tekintettel szolid averzióira az intézményes tudomány iránt, illetve a matematika történetének sokszor sajátos értelmezésére, mely szereti kiemelni, egyoldalúan recitálni a fogalmak szigorú definiálásával kapcsolatban az elhamarkodottságot, ignoranciát, vagy hezitálást tükröző idézeteket – inkább paradigmának és szemléletmódnak, semmint konkrét szaktudománynak tekintette. Megalkotóján kívül a szűkebb értelemben vett matematikusok viszonylag ritkán, és általában speciális kontextusban (pl. alapozó, bevezető kurzusok neveként) használják (bár egyre gyakoribb az ilyen értelmű előfordulása). Hutchinson cikke az iterált függvényrendszerekről a nyolcvanas évek elején valószínűleg az első lépést jelentette az önálló tudományággá váláshoz, a fraktálok elmélete valóban azonban sokkal inkább jelent nagyszerű természettudományos és informatikai alkalmazásokat, semmint kiemelt matematikai kutatást.
Elmondható továbbá, hogy a fraktálgeometria csekély, de egyre növekvő elméleti hátterének fogalmai és tételei többnyire olyan jellegűek, amik bármelyik tudományegyetemen tipikusan sokkal inkább az analízis, semmint a geometria tanszékek kurzusaihoz kapcsolhatóak. A „fraktálgeometria” elméleti háttere jóval inkább „fraktálanalízis” avagy „fraktálkalkulus”, illetve „fraktáltopológia”.
A geometriának jelenleg még nincs (és várhatóan nem is lesz) kifejezetten olyan ága, ami a fraktálok geometriájával foglalkozna (külön tanszékek, szaklapok, egyetemi kurzusok stb. csak szórványosan alakulnak ki): egy fraktálokkal foglalkozó jövendőbeli matematikai résztudomány sokkal könnyebben lesz a függvénytan (analízis) része) – ám jelenleg még az ilyen tárgyú cikkek meglehetősen szétszórtan jelennek meg halmazelméleti, analitikus topológiai, rendszerdinamikai, műszaki, fizikai, népszerűsítő stb. folyóiratokban és kiadványokban. Tény azonban, hogy a tradicionális, euklideszi geometria és differenciálgeometria eszközei, mint pl. a hagyományos módon, határértékként definiált ívhossz, terület és dimenzió nem alkalmasak a fraktálok jellemzőinek számszerűsítésére, mivel „végtelen nagy értékeket” adnak, azaz ezek a mérőmódszerek divergensek a fraktálokra alkalmazva, vagyis valóban szükség van új módszerek kifejlesztésére. Ez a folyamat napjainkban is tart.
Felbukkan továbbá az a tévhit is, hogy a „fraktálgeometria” nemeuklideszi geometria lenne; szórványosan még a szakirodalomban is előfordul.[17] Ennek ellenére, szó sincs ilyesmiről. Ez a vélemény Mandelbrot szavainak félreértéséből adódik, aki többször kijelentette, hogy „a fraktálgeometria a geometria egy teljesen új ága, éppen olyan jelentős felfedezés, mint Euklidesz Elemeinek az összeállítása az ókorban.” Ezek a szavak, tudománytörténeti szempontból nézve, teljesen korrektek, azonban ettől még a „fraktálgeometria” nem jelenti a párhuzamossági posztulátum (vagy más bevett geometriai axiómák) revízióját, vagyis azt a kutatási területet, amit a „nemeuklideszi geometria” kifejezés valójában jelent. A „fraktálgeometria” pusztán az euklideszi geometrián belül vizsgál nagyon bonyolult alakzatokat. Valóban éppen olyan jelentős lépés a geometriában, mint amit a görögök tettek az ókorban; de ez a lépés az euklideszi geometrián belül jelent továbbhaladást, nem pedig kívüle (elvileg nem kizárt, hogy a nemeuklideszi geometrián belül is vizsgáljanak fraktálokat, de ez egyelőre még nem jellemző).
A „fraktálgeometria” alkalmazásai és kulturális mozgalommá szélesedése[szerkesztés]

Mandelbrot „fraktálgeometriája” és könyvei a kritikusabb hangoknál sokkal jellemzőbben inkább váltottak ki csodálatot és elismerést, tudósok és laikusok körében egyaránt. Kiderült, hogy jóval, de jóval többről van szó annál, hogy képesek vagyunk-e a természet látványának alaktanát megérteni. A fraktálok nemcsak a természeti alakzatok vizuális leírása jók – bár kétségkívül ez is számos területen jelent komoly haladást. A fizika, kémia, biológia, a kozmológia, a pszichiátria, és még sok más tudományág képes komolyan hasznosítani őket. A kaotikus rendszerek, és matematikai ábrázolásaik, a fraktálok, lépten-nyomon előbukkannak a természet vizsgálatakor, olyan rendkívül távolinak tűnő, mindenesetre igencsak eltérő léptékű jelenségeket összekötve, mint az anyagi részecskék hőmozgása, a halmazállapot-változások, a kromoszómák DNS-láncaiból hiányzó génrészletek jellemzése,[18] a növények levélereinek, az emberi vérerek, idegek és tüdőhörgők mintázata,[19] a villámcsatornák elágazásai, az értéktőzsdék árfolyamingadozásai,[20][21] a Szaturnusz gyűrűrendszerének szerkezete, a galaxisok alakja, vagy akár az Univerzum kezdeti fejlődése.
A fraktálokkal való foglalkozás egyre közkeletűbb lett a huszadik század második felének végére, többek között a kiváló népszerűsítő munka hatására. Ennek példái a Scientific American magazin cikkei, Mandelbrot saját könyvei (1975-ben, 1977-ben, valamint, A természet fraktálgeometriája címmel, 1982-ben) és cikkei, illetve Michael Barnsley népszerű, Fraktálok mindenütt c., 1988-as műve. A tudományos és népszerűsítő munkák mellett kialakult a profi tudósok és profi művészek mellett laikusok által is széles körben terjesztett fraktálművészet. Az utóbbi széles körűvé válásához elengedhetetlen volt a személyi számítógépek elterjedésének a hetvenes-nyolcvanas években kezdődő forradalma.
Fraktáldimenzió[szerkesztés]
A geometriában hagyományosan egy síkgörbe egy-, egy felület két-, és egy térbeli test háromdimenziós. A görbéket az egyes dimenziójú alterekben elfoglalt méreteik jellemzik (ezek mérése a matematikai analízis, azon belül a topológia és ezen belül is a mértékelmélet, és a topológiának az analitikus geometriával való házasságából született tudományterület, a differenciálgeometria feladata): a görbéket az ívhossz és görbület, a felületeket a kerület és felszín, a testeket a felszín és térfogat jellemzi. Ahogy a fentebbi részekben említettük, a fraktálok esetében ezekkel a mérőszámokkal a legkülönfélébb problémák vannak: sok fraktál nem mérhető.
Mandelbrot egyik zseniális ötlete az volt, hogy a mérhetőség hiánya a geometria kiterjedésfogalmának túl egyszerű voltából fakad. A fraktálalakzatok azért nem mérhetőek, mert tulajdonképpen átmeneti állapotban vannak két egész térdimenzió között. A fraktálok egy részét és más nem mérhető alakzatokat azonban már jóval ezelőtt is vizsgálták a matematikusok, és ki is dolgoztak néhány új mérési eljárást, mint pl. az ún. Hausdorff-mérték[22] fogalmát (és egyebeket is), csakhogy éppenséggel az ilyen eljárások érdektelenségbe ütköztek, mivel nem voltak természettudományos felfedezések, melyek leírására alkalmazni lehetett őket, így egy-egy tudományágon belüli, szűk körben ismert elméleti tudásként leledztek egészen a nyolcvanas évekig. A fraktálokkal kapcsolatos felfedezések (ezek jó része jellemző módon műszaki intézetek alkalmazott matematikai laboratóriumaiban történt) mindezt megváltoztatta. Mandelbrot kutakodásai során rátalált a Hausdorff-mérték fogalmára, és az erre alapozott Hausdorff-Besicovich-dimenziójára, ami számos fraktál esetében elősegítette a matematikai leírást.
Az úgynevezett fraktálhalmazok esetén a dimenzió nem adható meg egyszerűen: ha közelítőleg kiszámítunk egy fraktális vonalat, akkor a kép egyre jobban kitölti a síkot, és az egydimenziós vonal egyre közelebb kerül ahhoz, hogy kétdimenzióssá váljon. Mandelbrot a Hausdorff-dimenziót használva megállapította, hogy a legtöbb fraktálkép dimenziója nem egész. Az általánosított dimenziónak ezt a változatát fraktáldimenziónak is nevezzük.
Ennek alapján Mandelbrot a következő definíciót adta a fraktálokra:
„A fraktál olyan halmaz, aminek a Hausdorff-dimenziója nagyobb, mint a Lebesgue-dimenziója.”
Ahol a vonal Lebesgue-dimenziója egy, a felületé kettő, és így tovább. Ez alapján számítva a fraktálok hossza vagy felszíne végtelen.
A Hausdorff-dimenzió kiszámolását a geometriailag szabályos (nem random) fraktálok esetében megkönnyítheti az ún. hasonlósági dimenzió kiszámítása. Ezt szemléletesen az adja meg, hogy hány példányra van szükség az adott alakzatból ahhoz, hogy kirakjuk az alakzat egy nagyobb példányát. Például a Sierpiński-háromszög, ami önmagának három felére kicsinyített példányából áll, így Hausdorff-dimenziója , míg Lebesgue-dimenziója 1. Lehet definiálni törtdimenziós mértékeket is; ekkor a Hausdorff-dimenzió az a legkisebb α szám, amire az alakzat α mértéke véges. A hasonlósági dimenzió az IFR-fraktálokra lett kidolgozva, és a fent leírtnál bonyolultabb módon is definiálható, hogy tetszőleges IFR fraktálra működjön, de sok esetben a fent leírt egyszerű meggondolás is elegendő a fraktáldimenzió kiszámításához. A hasonlósági definíció előnyös tulajdonsága, hogy általában megegyezik az alapesetben csak nagyon bonyolult módon számolható, elméleti célokra létrehozott Hausdorff-dimenzióval.
Ha egy fraktál önmagának egy meghatározott számú kicsinyített példányaiból áll, és a kicsinyítés aránya mindig ugyanannyi, akkor a D fraktáldimenzió így számítható:
Az önhasonlóság csak statisztikai értelemben is fennállhat. Ekkor véletlen fraktálokról van szó.
Absztraktabbul,
Ahol is jelöli a Hausdorff-dimenziót.
A hasonlósági dimenzió mellett másik fontos eszköz a Hausdorff-dimenzió egyszerűbb számolására, illetve becslésére a dobozszámláló-/dobozszámlálási-/doboz-/boxdimenzió, vagy más néven Minkowski-dimenziónak. A Minkowski-dimenzió két fontos előnye, hogy viszonylag egyszerű elméleti alapokra épül, ezért könnyű vele dolgozni és könnyen kiszámolható, valamint, hogy véletlen fraktálokra is alkalmazható, a hasonlósági dimenzióval ellentétben. A dimenziók alkalmazása ugyanakkor körültekintést kíván, mert nem pusztán számítási módokat, hanem hasonló, de némileg eltérő elméleti megalapozottságú mérőszámokat jelentenek. Elméleti megfontolás szempontjából a Hausdorff-dimenzió tekinthető elfogadhatónak, amelynek kiszámítása ugyanakkor meglehetősen komplikált. A Minkowski-dimenzió alkalmazása e tekintetben egyszerűbb.
Példák[szerkesztés]



A legegyszerűbb önhasonló objektumok a szakaszok, paralelogrammalemezek, tömör testként elképzelt kockák, mert oldalaikkal párhuzamosan önmaguk kisebb példányaira szeletelhetők. Mégsem fraktálok, mert határaik sima (differenciálható) függvényekkel írható le.
Az önhasonló fraktálokra példa a Sierpiński-háromszög, ami önmagának három felére kicsinyített példányából áll, így Hausdorff-dimenziója , míg Lebesgue-dimenziója 1.
Az önhasonlóság lehet közelítő, vagy érvényesülhet statisztikailag is. Ezáltal a fraktálgeometria sikeresen alkalmazható természeti objektumokra, így fákra, felhőkre, partvonalakra. Ezek többé-kevésbé önhasonló struktúrájuk van, de ez a hasonlóság nem szigorú. Az elemi geometria egyszerűbb alakzataival szemben, mint pl. a térelemek és sokszögek, a fraktálok részletei nem egyszerűbbek, mint az egész; ha kinagyítva tekintjük egy részét, akkor újabb és újabb részletek válnak láthatóvá.
Sok fraktál iteratív módszerekkel definiálható. Néhány lépés után már egyszerű szabályokkal is bonyolult minták kaphatók.
A Pitagorasz-fa négyzetekből épül fel, amik úgy helyezkednek el, ahogy azt a Pitagorasz-tétel ábrázolásai mutatják.
Egy másik fraktál a Newton-fraktál, ami Newton-módszerrel számítható.
A Menger-szivacs egy háromdimenziós térbe ágyazott fraktál.
Az egyik leghíresebb és legtöbbet tanulmányozott fraktálalakzat kétségkívül a Mandelbrot-halmaz. Számítógépes ábrái az új ismeretterület gyakori jelképévé váltak. Érdekesség, hogy ez az ikonikus alakzat maga sem törtdimenziós, Hausdorff-dimenziója pontosan 2, ebben az értelemben tehát nem számít fraktálnak Mandelbrot definíciókísérletéhez ragaszkodva. (Határvonala, amely egy végtelen hosszú zárt görbe, viszont fraktál.)
A fraktálszerűség a természetben is megjelenik. Sok természeti képződmény tekinthető közelítőleg fraktálnak, de a struktúra rendszerint nem tartalmaz három-öt lépcsőnél többet. A természetben fellelhető fraktálok önhasonlósága nem szigorú; csak közelítő jelleggel, és statisztikusan érvényesül. Ilyenek a fák, az érrendszerek, a folyórendszerek vagy a partvonalak. Nem lehet pontosan megmérni a partvonalak hosszát: minél pontosabban mérik, annál hosszabb lesz. Az olyan matematikai fraktál, mint a Koch-görbe esetén ez a hossz végtelen lenne.
Fraktálok generálása[szerkesztés]
Elméleti, leíró konstrukciós rendszerek[szerkesztés]
Sok eljárás eredményez fraktált, ezek az eljárások egytől egyig rekurzívak. Ilyenek:
- Az iterált függvényrendszerek és az L-rendszerek többnyire az olyan „geometrikus”, szigorúan önhasonló szabályos fraktálokat eredményezik, mint a Sierpiński-háromszög vagy a Koch-görbe. A két módszer által generált alakzatok osztályai közt nincs éles határ; de a síkidom-fraktálokat jellemzőbb módon IFR-ekkel, míg a görbe jellegű fraktálokat inkább L-rendszerekkel könnyű előállítani (tehát ha az alakzat mint síkbeli ponthalmaz fontos, akkor inkább az IFR, ha csak az alakzat határa a lényeges, akkor L-rendszer a kézenfekvőbb). Hangsúlyozzuk, hogy itt elméleti konstrukciós rendszerekről, tulajdonképp puszta formális nyelvekről van szó, amelyeknek számítógépes megvalósítása akár ugyanazokon az alacsony szintű grafikus algoritmusokon is alapulhat.
- Korlátossági halmaz jellegű fraktálok: Egy komplex változós függvény generálja őket. Erre a típusra példa a Mandelbrot-halmaz, a Julia-halmaz és a Ljapunov-fraktál. Az ábrán az egyes pontok színét régebben általában az adta, hogy hány lépés után kerülnek el egy bizonyos távolságra az origótól az újabb és újabb helyettesítések során, ezért szökésiidő-fraktáloknak nevezték őket, mára ez a név elavult.
- Véletlen fraktálok: véletlenszerű folyamatokkal generálják őket. Ilyenek például a perkolációs fraktálok, a Brown-mozgás, a fraktális tájképek és a Brown-fa.
Programok[szerkesztés]

Ami ezen módszerek gyakorlati megvalósítását illeti: ma már nemcsak speciálisan erre a célra kifejlesztett fraktálképgeneráló szoftverekkel, de a legtöbb rasztergrafikus stúdióprogram egyszerű (vagy bonyolult) szűrőivel is létre lehet hozni fájdalommentesen véges idő alatt fraktálképeket.
Kezdetben speciális és keveset tudó programokat fejlesztettek, pl. amik csak Mandelbrot-halmazokat (és, esetleg, Julia-féléket) tudtak rajzolni, és a megjelenítés, képalkotás minősége is hagyott hátra maga után kívánnivalókat. Az első elfogadható minőségű és még ma is fejlesztett és közhasználatban lévő, az MS-DOS érában dominánsnak számító program a Fractint volt.
A mai, még összetett fraktálrajzoló programok, mint pl. az Apophysis, az Incendia, az UltraFractal, ChaosPro figyelnek (egyre inkább) mind az előállítható formulák széles választékára, mind a képalkotás algoritmikus és grafikus optimalizálására. A legtöbb említett program ingyenesen is használható. A világhálón elérhető, többnyire ingyenes fraktálkészítő programok igencsak változatosak tudásban és minőségben, számos használhatatlan és számos briliáns is van közöttük. Elmondható, hogy a korlátossági halmazokat és rokon módszereket (Newton-iteráció) ábrázoló programok a legkidolgozottabbak, jóval kevesebb olyan létezik azonban, amelyek minőségi módon tudnának pl. L-rendszereket ill. véletlen fraktálokat létrehozni.
Ha nem is ennyire fejlett módon, de alkalmassá váltak fraktálképek készítésére a legújabb generációs ingyenes grafikai szoftverek is. Ilyen pl. a Paint.NET, amelyhez több fraktálokkal kapcsolatos plugin tölthető le. Az egyik ilyen pl. a Seamless Texture Maker (csempézésre alkalmas textúrát készítő szűrő), amely hasonlósági transzformációk egyszerű rendszerét hajtja végre a képen (azt felosztva kisebb cellákra, és mindegyikbe a kép egy kisebb változatát kicsinyíti le.[23][mj 8] Ez a példa azért érdekes, mivel félig-meddig kilóg a „képlettel megadható fraktál”, tehát a „fraktálművészet = algoritmikus művészet” szokásos hagyományából. A GIMP-nek is van számos fraktálok és más algoritmikus képek alkotására létrehozott szűrője, makrója és plugin filtere, köztük olyanok is, amik kifejezetten erre a célra készültek. Nevezetes példa még a Photoshop fractalius filtere, ami dacára a mögötte rejlő algoritmusnak, általában kifejezetten nem fraktálképeket készít.
Az L-rendszer[szerkesztés]
Az L-rendszer (Lindenmayer-rendszer) egy absztrakt formális nyelv, amely megfelelően értelmezve, alkalmas fraktálalakzatok generálására. A nyelvet Aristid Lindenmayer magyar származású biológus alkotta meg 1968-ban, aki a növények növekedési sémáit és morfológiai típusait akarta osztályozni vele. Az L-rendszer formuláit (sík)geometriai alakzatokként és transzformációkként értelmezve, minden, a rendszerben felírt formula egy alakzatot ad meg, köztük fraktálok is vannak.[24]
| Ezt a szakaszt át kellene olvasni, ellenőrizni a szövegét, tartalmát. További részleteket a cikk vitalapján találhatsz. |
Kiinduláskor F jelöli a szakaszt. A további iterációkban az előző lépésben előállított vonalat jelenti. Lényegében F helyére újra és újra beillesztjük az utasítássorozatot. R és L jobbra, vagy balra való lépést jelez, és +, – mutatja a forgásszög előjelét, vagyis azt, hogy az óramutató járásával ellentétesen, vagy azzal megegyező irányban kell venni a szöget. A | jel 180 fokos fordulatot jelent. Ha a szög jele egymás után többször szerepel, akkor a szög megfelelő többszörösét kell venni. Az X és az Y jelek rekurzívan helyettesített szimbólumok. [2] Archiválva 2014. július 14-i dátummal a Wayback Machine-ben
| Fraktál | L-rendszer | Szög | Szakaszarány | Ábra |
| Sárkánygörbe |
F → R vagy F → L R → +R—L+ L → -R++L- |
 | ||
| Gosper-görbe |
F → R vagy F → L R → R+L++L-R—RR-L+ L → -R+LL++L+R—R-L |
 | ||
| Hilbert-görbe |
X X → -YF+XFX+FY- Y → +XF-YFY-FX+ |
 | ||
| Koch-görbe, hópehelygörbe |
F—F—F F → F+F—F+F |
 | ||
| Peano-görbe |
X X → XFYFX+F+YFXFY-F-XFYFX Y → YFXFY-F-XFYFX+F+YFXFY |
 | ||
| Peano-görbe |
F F → F-F+F+F+F-F-F-F+F |
 | ||
| Penta Plexity |
F++F++F++F++F F → F++F++F|F-F++F |
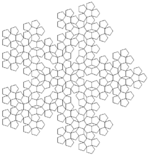 | ||
| Sierpiński-háromszög |
F → R vagy F → L R → -L+R+L- L → +R-L-R+ |
 | ||
| Sierpiński-háromszög |
FXF—FF—FF X → --FXF++FXF++FXF—F → FF |
 | ||
| Háromszög |
F—F—F F → F—F—F—ff f → ff |
 | ||
| Sierpiński-szőnyeg |
F F → F+F-F-FF-F-F-fF f → fff |
 | ||
| Lévy-C-görbe |
F F → +F—F+ |
 |
Példaként tekintsük a sárkánygörbét:
F → R R → +R–L+ L → -R++L-
F egy két pont közötti szakasz. F → R azt jelenti, hogy az F szakasz helyére R-et helyettesítünk. Ez azért kell, hogy elindulhasson az L-et és R-et váltakozva helyettesítő eljárás, ami a következőképpen folytatódik:
R +R–L+ +(+R–L+)--(-R++L-)+ +(+(+R–L+)--(-R++L-)+)--(-(+R–L+)++(-R++L-)-)+ . . .
Meghatározott számú helyettesítés után a sorozatot megszakítják, hogy felrajzolhassák az ábrát:
+(+(+r–l+)--(-r++l-)+)--(-(+r–l+)++(-r++l-)-)+
ahol r és l hossza előre meghatározott.
IFR-ek[szerkesztés]

1981-ben John E. Hutchinson matematikus publikált egy alapművé vált rövid cikket Fraktálok és önhasonlóság címmel.[25] Ebben a metrikus terek függvénytanának-topológiájának egyik eszközét, az iterált függvényrendszereket (IFS, iterated function system vagy IFR, iterált függvényrendszer) használta fel fraktálok generálására. Az iterált függvényrendszerek egy (teljes) metrikus tér fölött távolságkicsinyítő (kontrakció jellegű) transzformációk véges családjai, pl. affin kicsinyítéseké, vagy centrális hasonlóság jellegű kicsinyítéseké. Egy iterált függvényrendszer egy teljes metrikus tér felett tehát lényegében egy (f1, f2, ... , fm) véges függvényrendszer, melynek minden tagja kontrakció.
Bár a fogalom matematikai leírása igen elvont, valójában nincs szó semmi bonyolultról. Egy zárt háromszöglemez esetében, amelyet a középvonalai négy darab kis háromszögre darabolnak, tekintsük azt a három részháromszöget ezek közül, melyek valamelyik csúcsa közös az eredeti háromszög valamelyik csúcsával! Legyenek ezek súlypontja X,Y,Z és tekintsük azt a három középpontos hasonlóságot, melyeknek középpontjai épp ezek a súlypontok és kicsinyítési arányuk egyformán 1:2! Alkalmazva ezeket az eredeti háromszögre, a transzformációk képeinek uniója három darab kis háromszög, az eredeti háromszögből készíthető Sierpiński-háromszög első iterációja. A következő transzformálás a Sierpiński-háromszög második iterációját képezi, és így tovább. A végtelenségig iterálva a folyamatot, a Sierpiński-háromszög keletkezik.
Hutchinson fontos eredményeket bizonyított cikkében az IFS-ekről, például, hogy megfelelő alapalakzatból kiindulva, mindig létezik az eljárásnak egy „konvergenciahalmaza” (egy fraktálalakzat), a szakirodalomban bevett elnevezéssel attraktora vagy invariáns halmaza,[26] nevezetesen egy olyan A halmaz, amely megegyezik saját, a rendszer összes kontrakciója szerinti képének uniójával; és ez megfelelő feltételek mellett (ha az IFR minden kontrakciója hasonlóság) önhasonló. Az IFR-ek fogalmára alapozva szigorúan bizonyítható a fraktálok „hasonlósági dimenziójának” létezése.
Hutchinson bizonyította, hogy a szokásos, szemléletes fraktálkészítő iterációs eljárások eredménye, mint amikor egy háromszöglemezből a középháromszögének kivágásával, majd a lépés végtelenségig való ismétlésével képezzük a Sierpiński-háromszöget, mint ponthalmazsorozat, konvergál az IFR attraktor-alakzatához. Vizsgálta az IFR-ek tanulmányozása során kapott fogalmak és a Hausdorff-dimenzió összefüggéseit is. Az IFS generálta fraktálok azóta megkerülhetetlen részei a fraktálok tanulmányozásának.
Komplex változós iterációspálya/korlátosságihalmaz-fraktálok[szerkesztés]
A korlátossági halmaz fogalma[szerkesztés]
 |
 |
Adott egy egyszerű képlettel leírható (általában algebrai) komplex függvény, mint pl. f(z)=z2+z. Kiindulva egy adott c komplex értékből, behelyettesítjük ezt a képletbe, majd a kapott eredményt újra ugyanabba a képletbe, és így tovább. Eredményül egy véges komplex számsorozatot kapunk, amelyet a c pályájának nevezünk az illető függvényre nézve. A pálya többféleképp viselkedhet: elemei egyre nagyobbá válva, a végtelenségbe „szökhetnek”; de maradhatnak örökre korlátosak is, pl. periodikusan váltakozhatnak véges sok érték között, illetve tarthatnak egy határértékhez. A korlátos pályákat adó c konstansok összessége, halmaza az f függvény „korlátossági halmaza”, sok esetben fraktál. A fent adott f függvény esetében pl. a Mandelbrot-halmazt kapjuk.
Ha a „korlátossági halmazhoz” tartozó pixeleket feketére színezzük, a többit fehérre, akkor egy fekete-fehér ábrát kapunk. A korlátossági halmaz kiszámítása mint számítógépes eljárás gyorsítható különféle matematikai tesztszámításokkal, sok esetben egy pályakezdő számról az első néhány pályaeleme kiszámolása után már meg lehet mondani, hogy biztosan nem fog a korlátossági halmazhoz tartozni, és, például, a periodikus pályájú (pl. négy számítás után a kezdeti értékhez térő, tehát önmagát ismétlő) kezdőszámokról véges sok (pl. 4) iteráció után is biztosan lehet tudni, hogy ők meg elemei a korlátossági halmaznak. Például a Julia-halmazok ábrázolása esetében bizonyítható, hogy ha valamelyik iterált pixel a pályában eléri a 2 egységnyi origótól való távolságot, akkor az biztosan a végtelenbe fog távozni, azaz nem lesz része a bikróm fraktálképnek.
Megjegyezzük, hogy valós függvényekkel is lehet korlátossági halmazokat számolni; noha eredményül nem kettő, hanem egydimenziós korlátossági halmazok keletkeznek.
A szökési sebesség alapú színezésről[szerkesztés]

Az adott iterációszám alatt a teszten "kihullott" (nem-korlátos) kezdőértékeket az épp számolt iteráció számításakor akár ki is lehet színezni egy, az iterációhoz rendelt színnel egy előre megadott színpalettáról. Ily módon színpompás kétdimenziós képek keletkeznek, amelyeken a színek a pályák szökési gyorsaságától függenek. Ezért az ilyen fraktálképeket „szökésisebesség-fraktáloknak” is szokás nevezni.
Kezdetben ez volt a fraktálképek színezésének uralkodó módszere. Az ilyen képek általában jellegzetes „pszichedelikus” színösszeállításban tündökölnek (a korai, nyolcvanas évekbeli fraktálképekre jellemző volt), bár ez erősen függ a palettától is.
Megjegyezzük, hogy bár a szabályosság követelményéhez hozzátartozna, hogy az alkalmazott paletta gradiens jellegű legyen (azaz a szökési sebességhez színértéket rendelő függvény valamelyik színjellemzőre – az árnyalatra, a sötétségre stb.) monoton legyen, ez nem feltétlenül jellemző; sőt, a legtöbb fraktálképgenerátor-programon tetszőleges palettát be lehet állítani, minthogy ez fontos része a fraktálképek által adott vizuális élménynek. Tehát a sötétebb, vagy világosabb szín nem jelent automatikusan nagyobb, vagy kisebb szökési sebességet: bármi előfordulhat, és a pontos jellemzéshez ismerni kell a palettát és a program által végrehajtott hozzárendelési algoritmust.
Reprezentációs függvények: más színezések[szerkesztés]

A nyolcvanas évek óta sokat fejlődtek a grafikus hardverek és szoftverek, és a programozási tudás is sokkal köznapibbá vált. Ami régen a laboratóriumok privilégiuma volt, a jó felbontású és órák alatt elkészülő szökésisebesség-ábrák készítése, azt ma már nemcsak PC-ken, de egy mobiltelefonon is pillanatok alatt meg lehet valósítani. Mindez azt is eredményezte, hogy egyéb, laikusok által is felfedezhető és implementálható eljárások is születtek a korlátossági halmazok algoritmikus kiszínezésére. Ezeket bizonyos szerzők reprezentációs függvényeknek vagy -algoritmusoknak nevezik. Egy közismertté lett példa a Buddhabrot-fraktálok osztálya, amelyek a Mandelbrot-halmazt ábrázolják, csak éppen egy teljesen eltérő képalkotási eljárással, mint a szokásos.[27][mj 9] Ezek egy része a szökésisebesség-alapú színezés módosítása, más részük teljesen más állapotjelző paramétereken alapul.[28]
Perkolációs véletlen fraktálok[szerkesztés]
A perkolációs fraktálok megalkotására mind az L-rendszerek, mind az IFR-ek alkalmasak, ha az algoritmusokat véletlenszám-generátorok hozzáadásával nem-determinisztikussá módosítjuk.
Például, a determinisztikus Sierpiński-szőnyeg úgy készül, hogy egy fekete négyzetet kilenc darab, egyharmados kicsinyítésű négyzetre bontunk (az oldalharmadoló merőleges egyenesek által alkotott háló megrajzolásával), a középső kis négyzetet fehérre színezzük, majd az eljárást a kisebb négyzetekkel is a végtelenségig ismételjük. A perkolációs Sierpiński-szőnyegek megalkotásakor az eljárás úgy módosul, hogy nem feltétlenül a középső, hanem egy véletlenszerűen választott kis alnégyzetet (esetleg többet is, de mindig véletlenszerűen választva) színezünk fehérre, és az iteráció során is véletlenszerűen választunk.
A perkolációs fraktálok az L- és IFR-fraktálok geometriai szabályosságából sokat megőriznek; azonban szigorú értelemben már nem önhasonlóak vagy önaffinok.
Az elnevezés, „perkolációs”, a folyadékok átszűrésével kapcsolatos fizikai problémáról, a perkolációról kapta a nevét, amelyben a véletlen is szerepet játszik. Az emberi DNS-állománnyal kapcsolatos bizonyos problémák modellezése során is gyakorlati alkalmazást nyertek.
Véletlenségszimulációs és sejtautomata-fraktálok[szerkesztés]

Ebből az osztályból a legismertebb és legtöbbet idézett módszer az ún. diffúziólimitált aggregáció (diffúzió irányította felhalmozódás) számítógépes szimulálása eredményeképp kapott, véletlen jellegű fraktálgenerálás.
A diffúziólimitált aggregáció egy diszkrét jellegű rendszerben olyan folyamat, melynek során a rendszer elemei egy adott kezdeti „mozgási energiával” rendelkezve, szabadon mozoghatnak a térben, ám mozgás során veszítenek energiájukból és lassulnak (nulla energiánál megállnak). A mozgási energiát a rendszertérben szabadon diffundáló tápanyagból való tápanyagfelvételellel kell pótolniuk. A mozgási energiájukat elvesztett elemek makrostruktúrákat hoznak létre. A lehorgonyzást végső soron a tápanyag diffúzióját leíró differenciálegyenlet szabályozza: ahol sok tápanyag van, ott sok éhes száj gyűlik össze, ám, ha többen vannak, gyorsabban meg is eszik a tápanyagot, és többé nem képesek mozdulni. Így lehorgonyzott, fogyasztókból álló kicsapódási v. felhalmozódási (aggregációs) telepek jönnek létre.
Az ilyen folyamatok számítógépes szimulációja eredményeképp elágazó szálrendszerekből álló, szabálytalanul koncentrikus jellegű, fraktál jelleggel bíró alakzatok születnek. Vizsgálatuk a fizikából, illetve a biológiából indult ki, amikor felfedezték, hogy egy rendszer elemeinek véletlenszerű mozgásából nem csak az atomok és más részecskék mérettartományában alakulhatnak ki rendezett struktúrák, hanem a kémiában és a biológiában is nagy számban fordulnak elő ún. véletlenszerűen önszervező rendszerek. Pl. ilyen modellekkel lehet leírni bizonyos telepes szerveződésű élőlények (moszatok, baktériumok) telepeinek, vagy egy termeszvárnak a kialakulását, de közlekedési és településszerveződési problémákat is. A DLA-szimulációk és a hasonló „szoftverlaboratóriumi” kísérletek az ilyen jelenségek leegyszerűsítő modelljeiből alakultak ki, és azok hozzávetőleges megértése céljából születtek.[29]
A fraktálok elméletének alkalmazási lehetőségei[szerkesztés]

Tudomány és technológia[szerkesztés]
A matematikai és fizikai alkalmazások mellett a fraktálok számos részben vagy egészben megvalósult technológiai újítás alapjai lehetnek. Így például:
- komputergrafika: A természetben előforduló legtöbb alakzat nem szögletes és szabályos geometriai idom, hanem bonyolult struktúra, amely legalábbis statisztikus tekintetben fraktálként viselkedik. A fraktálok ráadásul rendkívül memóriaigénytelen, meglepően rövid matematikai formulák alakjában tárolhatóak, és viszonylag egyszerű az előállításuk. Ez ideális alannyá teszi őket a komputergrafika számára. Például egy fraktális alapon működő tájképgeneráló program fraktálformulából állíthat elő egy tájképtípust, amely biztosítja, hogy kevés erőfeszítéssel egy szabályos (e tekintetben nem valószerű), de nagyon komplex (tehát valószerű) képet alkosson, majd a szabályosság csökkentésére a formulából előálló képelemeket (ál)véletlen zajjal keveri. Így olyan képeket lehet előállítani, amelyek valószerűség tekintetében megdöbbentően megtévesztőek lehetnek. Hasonló lehetőség a 3D-s rajzprogramok esetében, hogy a szerkesztett 3D-objektumokat statisztikus fraktálformulával készült textúrával „vonják be”, ezáltal a felületek elegendően „érdesek” és „zajosak” lesznek, valószerű hatást keltve. Az első film, ahol felhasználták a fraktál alapú tájrenderelést, a Star Trek II: Khan haragja c. sci-fi volt (a jelenetet a Lucasfilm CGI-részlege készítette), ahol egy idegen bolygó tájait szimulálták a technológiával.
- digitális képfeldolgozás: folynak kísérletek képtömörítő, illetve képfelbontásnövelő szoftverek készítése irányába. Az ilyen szoftverek részben memóriakímélő formában tudnak nagy felbontású, adatigényes képi információkat tárolni, részben (ez a rész még mindig inkább csak elméleti szakaszban van) élesíteni, nagyítani tudnak (illetve „próbálnak” és „becsülnek”) egy képet anélkül, hogy a kép felbontása alapján elegendő információ állna rendelkezésre ehhez a művelethez. A nagyítás tehát becslés (extrapoláció) alapján történik.[30]
Egyes szoftverek digitális képfelbontásnövelésre is képesek lehetnek: ezt úgy érik el, hogy a kép alapján egy matematikai formulát készítenek, mintha a kép egy IFS függvényrendszer attraktora, azaz fraktálkép lenne; majd extrapoláció gyanánt valójában iteratív fraktálkép-renderelést végeznek.[31]
Fraktálok a kultúrában[szerkesztés]
Az önhasonló fraktálképeket a művészet – különösen a barokk – már a matematikai felfedezések előtt is használta. Ebből a hagyományból építkezett pl. az ötvenes évek mackósajt-dobozai fedőlapján látható magyar reklámgrafika, amelyen egy pincérnek öltözött mackó tálcán egy doboz mackósajtot hordoz, amelynek fedőlapján egy pincérnek öltözött mackó egy doboz mackósajtot hordoz, amelynek ... stb.[32] Világmagyarázó elméletek azonban csak Mandelbrot fellépése után épültek ezek köré a képek köré.
A fraktálok a nyolcvanas években bevonultak a matematikából a kultúrába is. Magyarországon ez egyfelől a Commodore 64, Sinclair Spectrum és más otthoni számítógépek terjedésének, másfelől a havonta megjelenő, magyar nyelvű Scientific Americannek volt köszönhető. E lap gyakran közölt képeket, kutatási eredményeket, rövid programokat és algoritmusokat, sőt egy különszáma kizárólag a káosszal és a fraktálokkal foglalkozott.
A fraktálok ismertségén és népszerűségén a nyolcvanas évek elejétől-közepétől kezdve nagyot lendített a PC-k elterjedése, illetve a tömegkultúrában való megjelenésük. Miután Steven Spielberg Jurassic Park című filmjében a pillangó-effektust megnevezték, szinte nem volt olyan, aki ne hallott volna róluk. Ekkoriban terjedtek el azok a szoftverek is, melyekkel egyszerűen (különösebb matematikai és informatikai ismeretek nélkül) bárki szinte tetszőleges fraktálképet generálhatott. Afféle szabadidős tevékenység (hobbi) lett ez, s bár a fraktálkép-készítők sokszor "művész"-ként definiálták magukat, ez vitatható. A szabadidős tevékenység mellett megszületett azonban a professzionálisabb fraktálművészet is.[33]
A professzionális képzőművészetben Saxon-Szász János képein megjelenő Polidimenzionális mezők nemcsak a dimenzió- és lépésváltásokat idézik meg, de sokat mondanak el a világ teremtéséről és változásáról, azaz a természetről. Alkotásai a konstruktivista művészet körébe sorolhatók.[34] A fraktálművészet digitális művészeti ágban Szlávics Alexa magyar festőművész a Püthagorasznak tulajdonított hangzókhoz tartozó számok és a számokhoz tartozó színek rendszere alapján egyedi fraktálmandalákat, valamint nemzetközileg elismert fraktálgrafikákat készít.
A fraktálok számos más művészeti ágra is hatással voltak, például a zenére, ékszerészetre.
Hivatkozások[szerkesztés]
Lásd még[szerkesztés]
Nevezetes fraktálok[szerkesztés]
Síkgörbék[szerkesztés]
- Cantor-halmaz
- Cantor-Lebesgue-függvény / Cantor-görbe
- Cantor-Volterra-Smith-halmaz
- Bolzano-függvény
- Hilbert-görbe
- Koch-görbe
- Peano-görbe
- Takagi-függvények
- Volterra-függvények
- Weierstrass-függvény
- Wiener-folyamat
Síkidomok[szerkesztés]
Testek[szerkesztés]
Fontosabb fraktálelméleti fogalmak és eszközök[szerkesztés]
- dimenzió
- iterált függvényrendszer
- káoszelmélet
- különös attraktor
- önaffinitás
- önhasonlóság
- skálafüggetlenség
Kulturális vonatkozások[szerkesztés]
Megjegyzések[szerkesztés]
- ↑ A gyűröttség olyan mértékű lehet, hogy a globálisan egydimenziós, görbe jellegű alakzat lokálisan többdimenziósként viselkedhet („térkitöltés”). Jellegzetes példa az ún. Koch-hópehelygörbe vagy a Mandelbrot-halmaz határoló görbéje. A szakadásosság is lehet olyan mértékű, hogy egy globálisan pl. kétdimenziós alakzat lokálisan egydimenziósként viselkedhet. Az alakzat „sűrűn” kitölt egy négyzetet, abban az értelemben, hogy a négyzettel közös pontjai semmilyen kézenfekvő egydimenziós görbére sem férnek rá, mindig marad egy ilyen görbén kívüli pont; azonban más szempontból nézve, a kitöltés annyira „ritka”, hogy a négyzet bármely kétdimenziós szeletét is vizsgálva, az alakzat azt nem „képes” hézagtalanul lefedni, tehát az alakzat sehol sem „lokálisan” kétdimenziós. Erre példa a Sierpiński-háromszög és a Cantor-halmaz. Ezek a paradox jelenségek vezettek a törtdimenziós mértékek (pl. a Hausdorff-dimenzió) fogalmának használatához.
- ↑ Egy képlettel való előállítását ld. pl. itt, 9.dia.
- ↑ A lépcső konstrukciója miatt a konstans részek összhossza (a végtelenségig) (ld. mértani sor összegzése).
- ↑ Ezzel kapcsolatos egy másik, némileg a Banach-Tarski-paradoxonra hasonlító érdekesség is: tekintve, hogy a görbe véges hosszúságú konstans szakaszokból áll, melyek összhosszúsága 1, a szemlélője kísértést érezhet rá, hogy a görbe hosszát 1-nek mondja, azon a szemléletes alapon, hogy minden konstans részt az y-tengellyel párhuzamosan az x-tengelyre tolva, a darabok uniója a 0 dimenziós Cantor-halmaz komplementere, azaz az unió 1-0=1 összhosszúságú. Azaz: „A) a görbe vetülete 1 hosszú, és B) a vetületet megfelelően feldarabolva, és minden darabot mérettartóan, eltolással a kellő magasságba mozgatva, azokból összeállítható a kérdéses görbe; C) Bármilyen vonal- ill. síkalakzatot akárhogy feldarabolva és a darabokat egybevágóságokkal mozgatva, amennyiben egy új alakzat keletkezik, a kapott alakzat hossza, ill. területe meg kell, hogy egyezzen az eredetivel; D) a Cantor-görbe hossza így megegyezik vetületének hosszával, ami 1. Q.E.D..” Sajnos, a C) megállapítás hibás, a Cantor-görbe rektifikálható, azaz mérhető ívhosszú ugyan, de hossza pontosan 2. A Banach-Tarski-paradoxonhoz hasonlóan, a gondolatmenetben lévő hibát az okozza, hogy a görbe végtelen sok darabra lett szétvágva, így a véges átdarabolásokra vonatkozó intuíciók tévedéshez vezethetnek.
- ↑ A magyar fordítás George Bruce Halsted angol fordítása (1913) nyomán készült.
- ↑ A kérdést azért is nehéz eldönteni, mert a tudományos elméletek komplex és egymásra épülő dolgok. Az, hogy egy gondolat mennyiben van kidolgozva, ezáltal melyik szerzőnél mondhatjuk, hogy nála már felfedezés, előtte pedig csak a dolgok előérzete, némiképp mindig szubjektív. A nagy felfedezések általában apró lépések egymásutánjai, és ezek összekapcsolódása sokszor csak utólag nyilvánvaló. Számos példa mutatja ezt: a Hélium mint elem kimutatása, a bakteriofágok felfedezése, a matematikában a nemeuklideszi geometria (veszekedéstől, sértődéstől sem mentes) vagy a differenciálszámítás (szintén prioritási vitába torkolló) megalkotása, vagy annak kérdése, hogy ki a modern, matematikai logika atyja (Frege, Russell, vagy épp Boole?).
- ↑ Krantz lovagiasan értesítette Mandelbrotot, hogy cikket ír róla, és úgy gondolták, hogy az eredetileg megcélzott folyóiratban, ahol Krantz cikkét már elfogadták közlésre, egyszerre jelentessék meg cikkeiket, a „megtámadott” viszontválaszával együtt. Ezt azonban a folyóirat vezetősége elutasította azon az alapon, hogy publikációs szabályzatuk kifejezetten tiltja a vita jellegű cikkeket, és a válaszcikk lehetőségét. Többszöri tárgyalás után, Krantz végül máshol jelentette meg cikkét.
- ↑ Sokszori, 10-20 lefuttatással, az újonnan keletkező képet hozzá kell rétegelni valamelyik réteg-egyesítési móddal a régihez
- ↑ Egy meglehetősen szofisztikált, nagy számítógépes-grafikai és matematikai tudást egyaránt mozgósító, a szökésisebesség-algoritmusoknál sokkal szebb eredményt adni képes színezés eljárást láss pl. itt: Pictures of Julia and Mandelbrot Sets. (Wikikönyvek, angol). Hiv. beill.: 2014-07-06.
Jegyzetek[szerkesztés]
- ↑ Dunbar, S. R.: Wiener Process (egyetemi jegyzet a Nebraska-Lincoln Egyetem Matematika Tanszékének honlapján, PDF). Ld. 3. old., „Transformations of the Wiener Process” c. fej. első bekezdése. Hiv. beill.: 2014-07-02.
- ↑ Benoit B. Mandelbrot: Object Fractals (könyv), 1975.
- ↑ Eredetiben: „Fractal geometry is the study of scale-invariant roughness”. Mandelbrot, B. B.: Gaussian Self-Affinity and Fractals ..., 9. old. Springer Science & Business Media, 2002 kiadású könyv Google könyvekbeli elektronikus változata. Hiv. beillesztése: 2014-07-01.
- ↑ a b Szabó László Imre: Ismerkedés a fraktálok matematikájával. Polygon könyvtár, Szeged, 1997. 64. old.
- ↑ Mandelbrot, B. B.: Gaussian Self-Affinity and Fractals ...; Springer Science & Business Media, 2002 kiadású könyv Google könyvek-beli elektronikus változata. Hiv. beillesztése: 2014-07-01.
- ↑ Ichiro Hauso: Coalgebric Representation Theory of Fractals Archiválva 2014. július 14-i dátummal a Wayback Machine-ben. (pdf). Hiv. beill.: 2014-07-07.
- ↑ Tommy Löfstedt: Fractal Geometry, Graph and Tree Constructions (MA záródolgozat / egyetemi jegyzet; pdf, 101 o.)
- ↑ Weierstrass, K.: Über continuirliche functionen eines reellen arguments, die für keinen werth des letzeren einen bestimmten differentialquotienten besitzen. Royal Prussian Academy of Sciences, 1872.
- ↑ MathWorld: Patological.
- ↑ Poincaré, H.: The Foundation of Science (A tudomány alapjai).
- ↑ Interjú a Mathematical People: Profiles and Interviews c. interjúkötetben, idézi IBM100.
- ↑ The Team - Benoit B. Mandelbrot. Az IBM100 / ibm.com (az IBM tulajdonában lévő kereskedelmi honlap). Hiv. beill.: 2014-07-06.
- ↑ Ian Stewart: Benoît Mandelbrot: from cauliflowers to cosmic secrets (B. Mandelbrot: brokkoliktól kozmikus titkokig). The Telegraph online változata (telegraph.co.uk Archiválva 2018. január 25-i dátummal a Wayback Machine-ben). 2014. júl. 5. Hiv. beill.: 2014-07-05.
- ↑ Horgan, John: Who Discovered the Mandelbrot Set? (Ki fedezte fel a Mandelbrot-halmazt?) - Scientific American online, 2009-03-13. Hiv. beill.: 2014-07-06.
- ↑ https://www.mimuw.edu.pl/~pawelst/rzut_oka/Zajecia_dla_MISH_2011-12/Lektury_files/Math.%20Intelligencer%201989%20Krantz.pdf
- ↑ Krantz, S. G.: Fractal Geometry. (reprint, pdf). Hiv. beill.: 2014-07-06.
- ↑ Russ, John C.: Fractal Surfaces. A Springer Science & Business Media kiadványának (1994) Google Könyvek-beli változata. 2. old. Hiv. beill.: 2014-07-02.
- ↑ Archivált másolat. [2014. július 14-i dátummal az eredetiből archiválva]. (Hozzáférés: 2014. június 28.)
- ↑ Losa, G. A. - Merlini, D. - Nonnenmacher, Th. F. - Weibel, E. R.: Fractals in Biology and Medicine (Mathematics and Biosciences in Interaction sor., IV. köt.). Springer, 2006. Elektronikus változat: Google könyvek. Hiv. beill.: 2014-07-01.
- ↑ Mandelbrot, B. B.: How Fractals Can Explain What's Wrong with Wall Street (Hogyan magyarázható fraktálokkal, mi minden rossz a Wall Streeten]. Scientific American Online, 1999/)
- ↑ [http: //www.google.hu/url?sa=t&rct=j&q=&esrc=s&source=web&cd=4&cad=rja&uact=8&ved=0CC8QFjAD&url=http%3A%2F%2Fwww.math.u-szeged.hu%2Ftagok%2Fkurusa%2F_site%2Findex.php%2Fteaching%2Fstud-downloadables%2Fcategory%2F6-ma-thesis%3Fdownload%3D48%3Afraktalok-a-tozsden&ei=W1SyU5q6BM2S7Aa9uIDwCQ&usg=AFQjCNG53onPXmOaDHYrDFETHdujM4c4KQ&sig2=C9vK2w9Qv0m4Bhl6GkH3fQ&bvm=bv.70138588,bs.1,d.bGE Fraktálok a tőzsdén] (szakdolgozat)
- ↑ Turner, Blackledge, Andrews: Fractal Geometry in Digital Imaging, 28-29. old.
- ↑ Seamless Texture Maker Archiválva 2014. szeptember 29-i dátummal a Wayback Machine-ben. Paint.Net plugin.
- ↑ Bővebben ld. pl.: Prusienkiewicz, Lindenmayer: The Algorythmic Beauty of Plants.
- ↑ Hutchinson, J. E.: Fractals and Self-similarity. 1981 (reprint), pdf. Hiv. beill.: 2014-07-03.
- ↑ Moór István: A Sierpiński-háromszög. szakdolgozat (ELTE, 2013).
- ↑ Robert Munafo: Representation Functions. (Egy alternatív színezési eljárás kódja). Mu-ency (egy Mandelbrot-halmazzal foglalkozó wikiwikiweb. Hiv. beill.: 2014-07-09.
- ↑ Megszülettek továbbá a 3D fraktálképeket renderelő szoftverek, a legjelentősebb a Mandelbulb nevezetű. Így ma már akár ki is lehet nyomtatni korlátossági tartományokat ábrázoló háromdimenziós fraktálszobrokat egy 3D nyomtatóval, noha az eljárás - maga a nyomtató - még drága.
- ↑ Vicsek Tamás: A természet geometriája Archiválva 2006. október 10-i dátummal a Wayback Machine-ben (pdf) - előadás írott változata / Élet és Tudomány cikk.
- ↑ Mansaré Anna Manty: Fraktálok és képtömörítés. Szakdolgozat (ELTE TTK, 2014). PDF, magyar nyelven. Hiv. beill.: 2014-07-05.
- ↑ Chainais, P. - Koenig, E. - Delouille, V. - Hochedez, J.-F. - Virtual super resolution of scale invariant textured images using multifractal stochastic processes Archiválva 2013. július 2-i dátummal a Wayback Machine-ben. (pdf). Hiv. beill.: 2014-07-05.
- ↑ [1].
- ↑ Perneczky Géza: Mennyire lehet matematikus a képzőművész?. Ponticulus Hungaricus, hiv. beill.: 2014-07-05.
- ↑ Perneczky Géza: Képzőművész a matematika és a „szép arányok” tartományai között. Ponticulus.hu. Hiv. beill.: 2014-07-05.
Források[szerkesztés]
Általános[szerkesztés]
- Fraktálok a természetben (engl.)
- Perneczky Géza:
- Mire jó a fraktálfilozófia? – a fraktálok és rokon területek eszmetörténete
- Fraktálok és eseményminták esszégyűjtemény, az előző írás kvázi folytatása.
- Hidden Dimensions Gallery – bevezető jellegű honlap és linkgyűjtemény (angol)
Matematika, fizika[szerkesztés]
- Csermely Péter előadásának egy részlete a skálafüggetlenségről és az önhasonlóságról
- Benoit Mandelbrot: Fractal Geometry -What is it?
- Frame – Mandelbrot – Neger: Fractal Geometry. Előadásvázlatok a Yale Egyetem honlapján a fraktálok elméletéről és alkalmazási lehetőségeiről.
- Mandelbrot Fractal Explorer barangolás a Mandelbrot-halmazban MapClient (OpenLayers)
- Újabb káprázatos matematikai alakzatok (Origó, 2010. március 1., a polinomok és gyökeik ábrázolásáról)
- Bourke, Paul: An introduction top fractals
Dokumentumfilmek:
- Arthur C. Clarke: The colours of Infinity (a Végtelenség színei, angolul)
- PBS Nova: Fractals – Hunting the Hidden Dimension (Fraktálok – Vadászat a rejtett dimenzió után, angolul)
További információk[szerkesztés]
- Az absztrakt művészet vonzereje, szentségtörése és szerepe az élethű virtuális valóság létrehozásában, mandadb.hu Hozzáférés ideje: 2019 január 11.
Könyv[szerkesztés]
- Benoit Mandelbrot:
- The Fractal Geometry of Nature. (A természet fraktálgeometriája). Freeman, San Francisco, 1982.
- Voß, Herbert: Chaos und Fraktale selbst programmieren, ISBN 3-7723-7003-9
- Horst Halling / Rolf Möller: Mathematik fürs Auge – Eine Einführung in die Welt der Fraktale, Spektrum, ISBN 3-86025-427-8
- Benoît B. Mandelbrot: Die fraktale Geometrie der Natur, Birkhäuser, ISBN 3-7643-2646-8
- Heinz-Otto Peitgen, Peter H. Richter: The Beauty of Fractals. Images of Complex Dynamical Systems, Springer, ISBN 0-387-15851-0 bzw. ISBN 3-540-15851-0
- Heinz-Otto Peitgen, Dietmar Saupe: The Science of Fractal Images, ISBN 0-387-96608-0
- Kenneth Falconer: FRACTAL GEOMETRY. Mathematical Foundations and Applications, Wiley 1997
Film[szerkesztés]
- Mandelbrot, B.: Fractals – The Art of Roughness (Fraktálok, avagy az egyenetlenség művészete) – rövid előadás a fraktálok felfedezéséről és mibenlétéről; TED, 2010, Hiv. beill.: 2014-07-06.
Jegyzet és egyéb[szerkesztés]
- Fractal Working Group (pdf)
- Mandelbrot, B – Frame, M.: The Transience and Technology of Fractals (pdf) – tömör összefoglaló a legfontosabb fraktálelméleti fogalmakról
- Vicsek Tamás: A természet geometriája
- Halley, J. M. – Hartley, S. – Kallimanis, A. S. – Kunin, W. E. – Lennon, J. J. – Sgardelis, S. P.: The Uses and Abuses of Fractal Methodology in Ecology (A fraktálokra épülő módszerek haszna és kára az ökológiai szakirodalomban). (PDF). Ecology Letters, 2004/7.; 254–271. o.
- Bourke, Paul: Google Earth Fractals (galéria fraktálszerű műholdképekből)
Fraktálképgeneráló alkalmazások[szerkesztés]
Freeware[szerkesztés]
- Apophysis – (Honlap) (Flame osztályú fraktálok)
- Chaoscope – (Honlap) (Attraktor fraktálok)
- Chaos Pro – (Honlap) (Szökési sebesség-, különös attraktor-, és kvaternió-fraktálok, zoom animációk)
- Fr0st – (Honlap) (flame fraktálok)
- Fractalizer – (Honlap)
- Fractal Explorer – (Honlap) (Korlátossági halmazok, IFS-ek, kvaterniófraktálok és még sok más fajta) (generátorformula-szerkesztővel)
- Fractal Forge – (Honlap) (Mandelbrot és más beépített korlátosságihalmaz-fraktálok, animációk támogatása)
- Fractice – (Honlap) (Mandelbrot-fraktálok és változataik) (Animációk támogatása)
- Fractint – (Honlap)
- Fractron9000 – (Honlap) (flame fraktálok)
- Fractsurf – (Honlap) – többféle korlátosságihalmaz-fraktál
- Fragmentarium – (Honlap) (nyílt forrás, bonyolult telepítési eljárás, kiegészítők szükségesek a futtatáshoz)
- Freego 0.11 – [3] (Animátor)
- Gnofract – (Honlap) – csak LINUX rendszerekhez
- IFS Illusions – (Honlap) (IFR-fraktálok)
- Incendia – (Honlap) – 3D fraktálépítő, számos extrával
- JWildfire – (Honlap) (Java alapú applet, flame fraktálok készítésére, számos extra)
- Kaos Rhei – (honlap) – (letöltőlink) – korlátossági halmaz-típusú fraktálok, többféle formula, egyedi beépített transzformációsformula-kezelő
- Sterling2 – (Honlap) freeware, a Sterling bővítése beépített generátorformula-szerkesztővel
- Tierazon vagy Tiera Zon – (letöltőlap) Archiválva 2014. november 10-i dátummal a Wayback Machine-ben (Korlátossági halmazok, több mint száz formula, beépített formulaeditor)
- Xaos – (Honlap) Magyarul is tudó, sokoldalú freeware fraktál generátor
- Saturn and Titan – Marc R. Eggleston szoftverei (fejlesztés alatt)
- Quat, Vchira – megszűnt fejlesztésű programok
[szerkesztés]
- Chaotica – (Honlap) (nem-kereskedelmi használatra ingyenesen és szabadon használható)
- Fractal eXtreme – (Honlap) (15 napos próbaidő; jelentéktelen különbségek – emlékeztetőképernyő és a zoom lehetőség némi korlátozása – a teljes verzióhoz képest)
- Fractal Science Kit – (Honlap) – számos típust ábrázol a korlátossági halmazoktól kezdve az L-rendszereken át egészen a hiperbolikus attraktorokig, makrók támogatása
- XenoDream – (Honlap) – nincs képmentés – 3D alakzatok, fraktálok és L-rendszerek
Egyéb[szerkesztés]
- Archaikus fraktálgeneráló programok
- Néhány fraktál, és Basicben írt programjuk
- Java alapú fraktálgenerátor és interaktív fraktál-galéria. (csak a legfrissebb Java-Browser-Plug-innel működik)
- YaFGen Archiválva 2009. július 5-i dátummal a Wayback Machine-ben – Java nyelven írt fraktálgenerátor különböző típusokra
- Visual Basic Programm Barnsely Farn – Falevelek generálása és még több más, szakdolgozattal
- Továbbiak ...
Művészet[szerkesztés]
- IFS Illusions – IFS fraktálgenerátor és galéria
- fraktalmuv.freebase.hu Archiválva 2007. szeptember 28-i dátummal a Wayback Machine-ben
- Saxon-Szász János oldala
- Quaternionische Fraktale[halott link] (PDF), szakdolgozat (1,84 MB)
- A fraktálok esztétikája, (PDF), Rafael Reiter
- Szlávics Alexa festő és fraktálművész oldala
























