Kocka

A kocka (vagy szabályos hexaéder) egy térbeli geometriai alakzat, egy speciális téglatest. 6 négyzet alakú lapja és 12 egyenlő hosszúságú éle van, amelyek 8 csúcsban találkoznak. A négyzet térbeli megfelelője. Hasáb, szabályos test.
Matematikai összefüggések[szerkesztés]
Egy élű kocka esetén
| felszíne | |
| térfogata | |
| beírható gömb sugara | |
| köréírható gömb sugara | |
| éleit érintő gömb sugara |
Szimmetriái[szerkesztés]
A kockának
- három négyfogású forgástengelye (szemben fekvő oldalak középpontjain át)
- négy háromfogású forgástengelye (testátlók)
- hat kétfogású forgástengelye (élfelező pontokon át)
- kilenc szimmetriasíkja
- egy szimmetriaközéppontja (középpont)
van.
Az identitást leszámítva a négyfogású tengelyek három-három, a háromfogású tengelyek két-két szimmetriát adnak. Összesen a kocka szimmetriacsoportjának 48 eleme van. Ez a kocka- vagy oktaédercsoport.
Descartes-koordináták[szerkesztés]
Egy origó közepű, 2 élhosszú, a tengelyekkel párhuzamos élű kocka csúcsainak koordinátái:(±1, ±1, ±1), aminek belsejét azok az (x0, x1, x2) pontok alkotják, ahol −1 < xi < 1.
Egyenlet R3-ben[szerkesztés]
A koordináta-geometriában az (x0, y0, z0) közepű és 2a élhosszú kocka azokat az (x, y, z) pontokat tartalmazza, amelyekre:
Mértani arányok[szerkesztés]

A kockának 11 lényegesen különböző testhálója van, csak úgy, mint duálisának, az oktaédernek. A lapok színezéséhez legalább 3 szín kell.
A kocka az egyetlen szabályos test, amivel a tér hiánytalanul kitölthető. A szabályos poliéderek között egyedül neki vannak páros oldalszámú lapjai, így az egyetlen platóni test, ami zonoéder, vagyis aminek minden lapja középpontosan szimmetrikus.
Kocka kontra oktaéder[szerkesztés]
- A kocka duális poliédere az oktaéder.
A kocka és az oktaéder segítségével további testek konstruálhatók, amiknek szintén az oktaédercsoport a szimmetriacsoportja:
- csonkított kocka, hat nyolcszög- és nyolc háromszöglappal
- kuboktaéder hat négyzet- és nyolc háromszöglappal.
A rektifikált kocka kuboktaéder.
- csonkított oktaéder hat négyzet- és nyolc hatszöglappal
Kocka és oktaéder egyesítéseként kapható
- a rombododekaéder 14 csúccsal és 12 rombuszlappal
- Az egységnyi élhosszú kocka duális oktaéderének élhossza .
| Szimmetria: oktaéderes [4,3], (*432) | [4,3]+ (432) |
[1+,4,3] = [3,3] (*332) |
[3+,4] (3*2) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| {4,3} | t{4,3} | r{4,3} r{31,1} |
t{3,4} t{31,1} |
{3,4} {31,1} |
rr{4,3} s2{3,4} |
tr{4,3} | sr{4,3} | h{4,3} {3,3} |
h2{4,3} t{3,3} |
s{4,3} s{31,1} |
| Az uniform poliéderek duálisai | ||||||||||
| V43 | V3.82 | V(3.4)2 | V4.62 | V34 | V3.43 | V4.6.8 | V34.4 | V33 | V3.62 | V35 |
A Dih4 diéderszimmetriával a kocka topológiai kapcsolatban áll a 4.2n.2n uniform poliéderekkel és parkettázásokkal, amelyek a hiperbolikus síkon folytatódnak:
| Szimmetria *n42 [n,4] |
Gömbi | Euklideszi | Hiperbolikus... | |||||
|---|---|---|---|---|---|---|---|---|
| *242 [2,4] D4h |
*342 [3,4] Oh |
*442 [4,4] P4m |
*542 [5,4] |
*642 [6,4] |
*742 [7,4] |
*842 [8,4]... |
*∞42 [∞,4] | |
| Csonkított alakzatok |
 4.4.4 |
 4.6.6 |
 4.8.8 |
 4.10.10 |
 4.12.12 |
 4.14.14 |
 4.16.16 |
 4.∞.∞ |
| Uniform duális alakzatok | ||||||||
| n-kisz alakzatok |
 V4.4.4 |
 V4.6.6 |
 V4.8.8 |
 V4.10.10 |
 V4.12.12 |
 V4.14.14 |
 V4.16.16 |
 V4.∞.∞ |
Mindezek oktaéderes szimmetriájúak.
Kapcsolatai más poliéderekkel[szerkesztés]


- A kocka egy tetszőleges csúcsát összekötve az ebben a csúcsban összefutó négyzetlapok nem szomszédos csúcsaival, szabályos tetraédert kapunk. Egy ilyen tetraéder térfogata a kocka térfogatának egyharmadát teszi ki. A maradék négy egybevágó, nem szabályos gúla (szintén tetraéder) térfogata egyenként a kocka térfogatának hatoda.
- A kocka csúcsai ily módon két, egymáshoz képest középpontosan szimmetrikus szabályos tetraédert határoznak meg. (Ezek metszete oktaéder.)
- A kocka hat négyzet alapú gúlára osztható úgy, hogy szimmetriaközéppontját a csúcsokkal összekötő szakaszok mentén szétvágjuk. Ha ezeket egy másik kocka lapjaihoz illesztjük, akkor rombododekaédert kapunk.
A kocka dodekaéderbe írható úgy, hogy a kocka csúcsai a dodekaéder csúcsaira illeszkednek, és a kocka élei a dodekaéder lapátlói.
- Az antipodális leképezés egy félkockát ad, ami egy projektív poliéder.
A kocka több általánosabb poliédernek is speciális esete:
| Név | Egyenlő élhosszak | Egyenlő élek | Derékszögek |
|---|---|---|---|
| Kocka | igen | igen | igen |
| Romboéder | igen | igen | nem |
| Kuboid | nem | igen | igen |
| Paralelepipedon | nem | igen | nem |
| Általános négyszöglapú hexaéder | nem | nem | nem |
A kocka topológiai kapcsolatban áll a 3 csúcsalakzatú gömbi poliéderekkel és parkettázásokkal:
| Gömbi poliéderek |
Szabályos poliéderek | Euklideszi | Hiperbolikus parketták | |||||
|---|---|---|---|---|---|---|---|---|
 {2,3} |
 {3,3} |
 {4,3} |
{5,3} |
 {6,3} |
 {7,3} |
 {8,3} |
... |  (∞,3) |
A kocka kapcsolódik a négyzetes parkettázásokhoz is, amelyek a hiperbolikus síkon folytathatók: {4,p}, p=3,4,5...
 {4,3} |
 {4,4} |
 {4,5} |
 {4,6} |
 {4,7} |
 {4,8} |
... |  {4,∞} |
A kocka a rombikus poliéderek és csempézések azon sorozatába is beletartozik, amelynek szimmetriája az [n,3] Coxeter-csoport. A kocka tekinthető rombikus hexaédernek, ahol a rombuszok négyzetek.
| Szimmetria *n32 [n,3] |
Gömbi | Euclidean | Hiperbolikus parketta | ||||
|---|---|---|---|---|---|---|---|
| *332 [3,3] Td |
*432 [4,3] Oh |
*532 [5,3] Ih |
*632 [6,3] p6m |
*732 [7,3] |
*832 [8,3] |
*∞32 [∞,3] | |
| Félig szabályos alakzatok Konfiguráció] |
 3.3.3.3 |
 3.4.3.4 |
 3.5.3.5 |
 3.6.3.6 |
 3.7.3.7 |
 3.8.3.8 |
 3.∞.3.∞ |
| Duaális (rombikus) alakzatok Konfiguráció |
 V3.3.3.3 |
 V3.4.3.4 |
 V3.5.3.5 |
 V3.6.3.6 |
 V3.7.3.7 |
 V3.8.3.8 |
 V3.∞.3.∞ |
A kocka négyzet alapú hasáb:
| Szimmetria | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|
| Kép | ||||||||||
| Gömbi poliéderként | ||||||||||
| Kép | ||||||||||
Trigonális trapezoéderként a kocka beletartozik a hatszöges diéderszimmetriájú poliéderek családjába.
| Szimmetria: diéder [6,2], (*622) | [6,2]+, (622) | [1+,6,2], (322) | [6,2+], (2*3) | ||||||
|---|---|---|---|---|---|---|---|---|---|

|

|

|

|

|

|

|

| ||
| {6,2} | t{6,2} | r{6,2} | 2t{6,2}=t{2,6} | 2r{6,2}={2,6} | rr{6,2} | tr{6,2} | sr{6,2} | h{6,2} | s{2,6} |
| Uniform duálisok | |||||||||

|

|

|

|

|

|

|

|

|

|
| V62 | V122 | V62 | V4.4.6 | V26 | V4.4.6 | V4.4.12 | V3.3.3.6 | V32 | V3.3.3.3 |
 Három kocka |
 Öt kocka |
Térkitöltések[szerkesztés]
A tér 28 konvex uniform rácsszerkezete közül 9 kapcsolódik a kockához:
Merőleges vetületei[szerkesztés]
A kockának négy merőleges vetülete van, aminek középpontja csúcs, élfelező, lapközéppont és a csúcsalakzatának normálisa. Az első és a harmadik rendre megfelel az A2 és a B2 Coxeter-síkoknak.
| Középpont | Lap | csúcs |
|---|---|---|
| Coxeter-sík | B2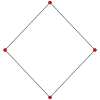
|
A2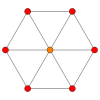
|
| Projektív szimmetria |
[4] | [6] |
| Nézetek | 
|

|
Általánosítása[szerkesztés]
A kocka tetszőleges dimenziós analogonjait szintén kockának nevezik. Ezek is szabályos politópok. Az n dimenziós kockának darab k dimenziós határoló lapja van. Speciálisan,
- egydimenziós kocka (szakasz): 2 csúcs, 1 él
- kétdimenziós kocka (négyzet): 4 csúcs, 4 él, 1 lap
- négydimenziós kocka (tesszerakt): 16 csúcs, 32 él, 24 lap, 8 térlap
- n dimenziós kocka: csúcs, él, lap, térlap, és oldal
Az n dimenziós kocka egy modellje az Rn vektortérbeli In egységkocka.
Az egységkocka
- , az egységintervallum n-szeres Descartes-szorzata
- a 2n csupa 0 - 1 koordinátájú pont konvex burka
- a 2n és a alakú féltér metszete
Az egységkocka élhossza 1, élei párhuzamosak a koordinátatengelyekkel, és egyik csúcsa az origó.
A kocka egy másik modellje az a kocka, aminek csúcsai a (±1, ±1,… ±1) Descartes-koordinátájú pontok. Ennek a belseje azokból a pontokból áll, amik összes koordinátájára −1 < x i < 1.
A kocka öt négy dimenziós uniform politópot határol:
| Tesszerakt, hiperkocka | Cantellated 16-cella | Runcinated tesszerakt | Cantitruncated 16-cella | Runcitruncated 16-cella |

|

|
|

|

|
A kombinatorikában[szerkesztés]
Egy másik fajta kocka a kockagráf. Ennek csúcsai a kocka csúcsainak, élei a kocka éleinek felelnek meg. Általánosítása a hiperkockagráf.
Egy másik általánosítás a háromdimenziós Hamming-gráf. A kockagráf a d = 2 esetnek felel meg. A Hamming-gráfokat és a hiperkocka gráfokat a párhuzamos programozásban használják ahhoz, hogy az egyes processzorok elég jól össze legyenek kötve, és az elméletek számára is könnyen kezelhető architektúrát adjanak.
Legyen S q elemű halmaz, és d pozitív egész. A H(d,q) Hamming-gráf csúcsai az S halmaz elemeinek d-esei. Két csúcs szomszédos akkor és csak akkor, ha egy koordinátában különböznek.
Előfordulása, alkalmazásai[szerkesztés]


- A kubán nevű szerves vegyület váza kocka alakú. Erről is kapta a nevét (angol: cube).
- Legismertebb alkalmazása a hagyományos dobókocka. A szerepjátékokban, ahol más dobótesteket is használnak, K6 néven emlegetik.
- Rubik Ernő világhírű találmánya szintén kocka alakú.
- A köznyelvben a kétdimenziós, négyzethálós mintát is kockásnak nevezik. Például kockás füzet, kockás ing, kockás piton.
Források[szerkesztés]
- A kocka és a kocka testhálójának különféle ábrázolásai
- Kockarejtvények
- Magasabb dimenziós kockák interaktív ábrázolása
- Weisstein, Eric W.: Cube (angol nyelven). Wolfram MathWorld
- Interaktív kockamodell
- K.J.M. MacLean, Az öt szabályos test és a többi félig szabályos test geometriai elemzése
- Uniform poliéderek
- Poliéderek a virtuális valóságban
- A kocka térfogata interaktív animációval







![{\displaystyle \lim _{n\to \infty }\left[(x-x_{0})^{n}+(y-y_{0})^{n}+(z-z_{0})^{n}-a^{n}\right]=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f460c5d5b865d5bd73cf6a505518ace038b7bc3)


















![{\displaystyle I^{n}=[0,1]\times \cdots \times [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62fa17f870540204d44b501791c78c5cadd0f77f)

