Dodekaéder

Szabályos dodekaéder

A dodekaéder egy poliéder tizenkét lappal.

• Általában a szabályos dodekaédert értik a „dodekaéder” szó alatt, vagyis azt a szabályos testet, melyet 12 szabályos ötszög alkot, melyek közül minden csúcsban három találkozik. Ennek 20 csúcsa és 30 éle van, duálisa az ikozaéder. A szabályos dodekaéder nem kristálycella, mert ezt az ötfogású szimmetriák lehetetlenné teszik.
• A rombododekaédernek 12 rombuszlapja, 24 éle és 14 csúcsa van. A gránátok jellegzetes formája.
• A trigondodekaédernek 12 trigonlapja, 18 éle és 8 csúcsa van.
• A nagy dodekaéder egy konkáv test, 12 pentagramma lappal.
• A köbös pentagondodekaéder egy szabálytalan dodekaéder, aminek minden lapjának van egy, a többinél hosszabb éle. Összesen 6 hosszú éle van. Így csak a köbös szimmetriák valósulhatnak meg. Ilyen alakúak a pirit kristályai.

A szócikk a továbbiakban a szabályos dodekaédert tárgyalja.

Szimmetriái

Pentagondodekaéder (sárgával) és duális teste, az ikozaéder (zölddel)

Platóni szabályos test, mert a lapjai, élei és csúcsai átvihetők. Szimmetriái hat ötfogású forgástengely (a szemközti lapok közepein át), tíz háromfogású forgástengely (a szemközti élek közepein át), tizenöt kétfogású forgástengely (a szemközti csúcsokon át), tizenöt szimmetriasík és középpontos szimmetria.

Szimmetriacsoportja a dodekaédercsoport, 120 elemmel, amit ikozaédercsoportnak is hívnak, és I_h-val jelölnek. Ebben a forgatások 60 elemű részcsoportot alkotnak, ami a legkisebb nem Abel egyszerű csoport, és a legnagyobb nem Abel normálosztó az összes szimmetria csoportjában. Izomorf az öt hosszú páros permutációk $A_{5}$ csoportjával. A teljes dodekaédercsoport szerkezete $A_{5}\times C_{2}$, mivel a középpontos tükrözés felcserélhető a forgatásokkal. Ez a csoport az [5,3] Coxeter-csoport.

Mivel szimmetriáiban szerepel az ötös szám, ezért ez a csoport összeegyeztethetetlen a hézagmentes térkitöltéssel, így nincs ilyen szimmetriájú kristályrács. A kvázikristályokban azonban előfordulnak dodekaéder alakú cellák.

Felszín és térfogat

A dodekaéder hálója

Az a élhosszú szabályos dodekaéder A felülete és V térfogata a következőképpen számítható ki:

$A=3{\sqrt {25+10{\sqrt {5}}}}a^{2}\approx 20.6457288a^{2}$

$V={\frac {1}{4}}(15+7{\sqrt {5}})a^{3}\approx 7.66311896a^{3}$

Dodekaéder gömbben és körülötte

A dodekaéder a élének függvényében a köré írható gömb r_u sugara és a beírható gömb r_i sugara a következőképpen számítható ki:

$r_{u}={\sqrt {3}}{\frac {1+{\sqrt {5}}}{4}}a\approx 1.401258538a$

$r_{i}={\frac {1}{2}}{\sqrt {\frac {25+11{\sqrt {5}}}{10}}}a\approx 1.113516364a$

azaz

$r_{u}=a\,{\frac {\sqrt {3}}{2}}\varphi$

$r_{i}=a\,{\frac {\varphi ^{2}}{2{\sqrt {3-\varphi }}}}$

ahol φ az arany arány.

Descartes-koordináták

Az alábbi Descartes-féle koordinátákkal definiálhatók az origó központú dodekaéder csúcsai:

(±1, ±1, ±1)

(0, ±1/φ, ±φ)

(±1/φ, ±φ, 0)

(±φ, 0, ±1/φ),

ahol φ= (1+√5)/2, az aranymetszés arányszáma (fi-szám). Az oldalhossz: 2/φ = −1+√5.

A dodekaéder diéderes szöge: 2arctan(φ), ami kb. 116,565 °.

Mértani arányok

A szabályos dodekaéder a csonkolt trapezoéderek végtelen halmazának harmadik tagja. Ezeket úgy képezhetjük, hogy egy pentagonális trapezoédert csonkolunk a két tengely-csúcsánál.

A dodekaéder élei közül kiválasztható három egymással szemben fekvő élpár úgy, hogy három egybevágó, páronként ortogonális téglalapot feszítsenek ki. A kimaradt nyolc csúcs ekkor egy dodekaéderbe írt kocka csúcsa. Összesen öt ilyen helyzet van, ahol minden él egy ilyen élhármasba tartozik, és minden csúcs kétszer kerül fel egy kockára. A dodekaéder szimmetriacsoportjának 5!=120 eleme hat mindezekre.

Mivel a beírt kockák élei az ötszöglapok átlói, ezért a dodekaéder élhossza és a kocka élhossza az aranymetszés szerint aránylik egymáshoz.

Lényegesen különböző hálóinak száma 43 380.

Az ugyanolyan térfogatú szabályos poliéderek közül a dodekaéder élhossza a legkisebb.

A dodekaéder lapjai 4 színnel színezhetők.

A lapátlók hossza az élhossz φ-szerese.

A dodekaéder három csillaga a négy Kepler-Poinsot poliéder közé tartozik.

A rektifikált dodekaéder egy ikozidodekaéder.

Ikozaéder kontra dodekaéder

Ha egy dodekaédert rajzolunk egy gömb belsejébe, a gömb térfogatának nagyobb részét (66,49%) foglalja el, mint egy ugyanabba a gömbbe helyezett ikozaéder (60,54%).

A szabályos egységnyi élhosszú dodekaéder térfogata több mint három és félszerese egy azonos élhosszú ikozaéder térfogatának. Az egységnyi oldalhosszú dodekaéder duális ikozaéderének élhossza φ.

A dodekaéder lapjainak száma 12, csúcsainak száma 20. Az ikozaédernek 20 lapja és 12 csúcsa van. Mindkét test 30 éllel bír.

Az uniform ikozaéderes poliéderek családja

Symmetry: [5,3], (*532)							[5,3]+, (532)
{5,3}	t{5,3}	r{5,3}	2t{5,3}=t{3,5}	2r{5,3}={3,5}	rr{5,3}	tr{5,3}	sr{5,3}
Az uniform poliéderek duálisai
V5.5.5	V3.10.10	V3.5.3.5	V5.6.6	V3.3.3.3.3	V3.4.5.4	V4.6.10	V3.3.3.3.5

A rombotriakontaédernek 12 + 20 = 32 csúcsa és 30 rombuszlapja van. A kétféle csúcs közül az egyik típusban három, a másikban négy él fut össze. A test úgy keletkezik, hogy a dodekaéder minden lapjára egyenes gúlákat teszünk úgy, hogy a szomszédos gúlák összeérő lapjai rombuszokat alkossanak.

Kapcsolatai más testekkel

A szabályos dodekaéder topológiailag az n³ csúcsalakzatú parkettázásokhoz tartozik.

Gömbi Poliéderek	Poliéderek			Euklideszi	Hiperbolikus csempézés
{2,3}	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	...	(∞,3)

Uniform oktaéderes poliéderek

Szimmetria: oktaéderes [4,3], (*432)							[4,3]+ (432)	[1+,4,3] = [3,3] (*332)		[3+,4] (3*2)
{4,3}	t{4,3}	r{4,3} r{31,1}	t{3,4} t{31,1}	{3,4} {31,1}	rr{4,3} s2{3,4}	tr{4,3}	sr{4,3}	h{4,3} {3,3}	h2{4,3} t{3,3}	s{4,3} s{31,1}
Az uniform poliéderek duálisai
V43	V3.82	V(3.4)2	V4.62	V34	V3.43	V4.6.8	V34.4	V33	V3.62	V35

Szférikus		Hiperbolikus parketták
{2,5}	{3,5}	{4,5}	{5,5}	{6,5}	{7,5}	{8,5}	...	{∞,5}

A dodekaéder a V3.3.3.3.n csúcsalakzatú nem uniform testek és parkettázások sorozatának is tagja. Ezeknek a laptranzitív alakzatoknak (n32) forgásszimmetriájuk van.

A 3.3.3.3.n snub poliéderek és parketták családja

Symmetry n32 [n,3]+	Szférikus				Euklideszi	Hiperbolikus
	232 [2,3]+ D3	332 [3,3]+ T	432 [4,3]+ O	532 [5,3]+ I	632 [6,3]+ P6	732 [7,3]+	832 [8,3]+	∞32 [∞,3]+
Snub alakzat	3.3.3.3.2	3.3.3.3.3	3.3.3.3.4	3.3.3.3.5	3.3.3.3.6	3.3.3.3.7	3.3.3.3.8	3.3.3.3.∞
Schläfli	sr{2,3}	sr{3,3}	sr{4,3}	sr{5,3}	sr{6,3}	sr{7,3}	sr{8,3}	sr{∞,3}
Snub duális alakzat	V3.3.3.3.2	V3.3.3.3.3	V3.3.3.3.4	V3.3.3.3.5	V3.3.3.3.6	V3.3.3.3.7	V3.3.3.3.8	V3.3.3.3.∞

Merőleges vetületek

A dodekaéder két merőleges vetülete az élek és a lapok középpontjain át vetítve az A₂ és H₂ Coxeter-síkokat adva:

Merőleges vetületek

Minek a közepe	Csúcs	Él	Lap
Kép
Projektív szimmetria	[[3]] = [6]	[2]	[[5]] = [10]

A dodekaéder egy lap felől nézett perspektív vetülete Schlegel-diagrammal síkgráfként, sztereografikus projekcióval gömbi poliéderként szemléltethető. Ezeket szokták használni a 120-cella négy dimenziós szabályos poliéder szemléltetéséhez is, amit 120 dodekaéder határol.

Vetület	Merőleges vetület	Perspektív vetület
		Schlegel-diagramm	Sztereografikus vetület
Dodekaéder
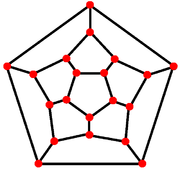
Dodekaplex

Csúcsok elrendeződése

A dodekaéder csúcselrendeződése megegyezik négy konkáv uniform poliéderével és három uniform összetett testével.

nagy csillag-dodekaéder	kis ditrigonális ikozidodekaéder	ditrigonális dodekadodekaéder	nagy ditrigonális ikozidodekaéder
Öt kocka	Öt tetraéder	Tíz tetraéder

Csillag alakzatok

A dodekaéder csillagai mind konkáv reguláris Kepler-Poinsot poliéderek.

	0	1	2	3
Csillag alakzat	Dodecahedron	Kis csillagdodekaéder	Nagy dodekaéder	Nagy csillagdodekaéder
Lapdiagram

Gráf

Egy Hamilton-kör a dodekaéderen

A dodekaéder váza tekinthető gráfnak is, ahol a poliéder csúcsai a gráf csúcsai, és a poliéder élei a gráf élei. Ez a gráf megegyezik a G(10, 2) általánosított Petersen-gráffal. A poliéder szimmetriái tükröződnek a gráfban, így az távolságreguláris, távolságtranzitív és szimmetrikus, automorfiacsoportjának rendje 120. A csúcsok és az élek 3 színnel színezhetők, az átmérő 5.

A gráf Hamilton is, azaz van benne Hamilton-kör, ami minden csúcsán áthalad. Maga a Hamilton-kör is innen származik, mert William Rowan Hamilton 1857-ben tervezett egy játékot, aminek célja egy Hamilton-kör megtalálása a dodekaéderen.

Alkalmazásai

Dodekaéder mint dobókocka

Megaminx

Dodekaéder alakú tárgyakat a gyakorlatban többször is használtak, és a művészetekben és a filozófiában is szerephez jut.

A dodekaéder az utoljára felfedezett szabályos test. Iamblikhosz szerint Hippaszoszt emiatt fojtották tengerbe.

• Egyes geodetikus kupolák a dodekaéderből levezethető poliédereket formáznak. Ezek a testek a dodekaéder lapjait osztják fel egyenlő szárú háromszögekre.
• Vannak dodekaéder alakú dobókockák is.
• Az újrahasznosítandó anyagokat egyes helyeken, például Párizsban dodekaéder alakú konténerekbe gyűjtik.
• Az épületakusztikában dodekaéder alakú hangosbeszélőkkel érnek el jó gömbkarakterisztikát.
• Dodekaéder alakú világítótestek
• A római pentagondodekaéder ismeretlen célra készült. Európában több helyen is megtalálható a római romok között.
• Tizenkét lapja miatt naptárnak is alkalmas: minden hónap külön lapot kap.
• A Megaminx és az Alexander’s Star a Rubik-kockához hasonló logikai játékok.
• A Contact című 1997-es tudományos-fantasztikus filmben a transzportgömb egy dodekaéder alakú rácsba van beágyazva.
• Egyes kvázikristályok dodekaéder alakúak. Vannak szabályos kristályok, amelyek dodekaéderesen kristályosodnak, igaz, ez vagy a nem szabályos pritoéder vagy a rombododekaéder.
• Hollandiában a Dodecahedron egy avantgárd fekete metálbanda.
• Egy élilleszkedésű, egybevágó dodekaéderekkel épített, akár végtelen nagyságú dodekaéderes szerkezet is építhető az Almássy-féle ikozaéder gráfcsúcsaiba helyezett egyforma, dodekaéderekből épült szerkezetekkel.

A 20. század művészetében M. C. Escher több képén is megjelenik. Salvador Dalí El sacramento de la Última Cena képén az utolsó vacsora helyszíne egy átlátszó dodekaéder.

Az Immersive media Dodeca 2360 kamerája az első 360 fokos látószögű, teljes mozgású kamera, amely képes minden irányból szimultán nagy felbontású felvételeket készíteni másodpercenként több, mint 100 millió pixeles felbontással vagy másodpercenként 30 képes sebességgel. A dodekaéderen alapul.

A The Phantom Tollbooth című gyermekeknek írt regényben a dodekaéder a matematika világának szereplőjeként jelenik meg. Minden lapján más szó áll, és úgy fordul, hogy azt mutassa a beszédpartnerének, amit érez.

Az univerzum alakja

Platón dialógusában Timaiosz a többi négy szabályos testet a négy elemhez, a dodekaédert pedig az univerzum isteni tervéhez hasonlította. Arisztotelész szerint az ötödik elem az éter, de ő nem állított fel ilyen kapcsolatot.

Bertrand Russell 1954-es novellájában, a "THE MATHEMATICIAN'S NIGHTMARE: The Vision of Professor Squarepunt"-ban az ötös szám ezeket mondja magáról: „Öt ujj van egy kézen. Én alkotom az ötszögeket és a pentagrammákat. Nélkülem nem lenne dodekaéder, és ahogy mindenki tudja, az univerzum dodekaéder alakú. Tehát nélkülem nem lenne univerzum.”

A tudományban számos javaslat született az univerzum globális alakjára. A primitív geometriák mellett felvetődött a Poincaré-féle dodekaédertér, egy pozitív görbületű tér, amelynek szemközti lapjai egy kicsit elforgatva azonosítva vannak. Ezt Jean-Pierre Luminet és társai javasolták 2003-ban, majd 2008-ban meg is becsülték az elforgatás lehetséges mértékét.

Lásd még

• Csonkított dodekaéder
• Pentakis dodekaéder
• Hamilton-út

Források

A Wikimédia Commons tartalmaz Dodekaéder témájú médiaállományokat.

• Weisstein, Eric W.: Dodecahedron (angol nyelven). Wolfram MathWorld
• Weisstein, Eric W.: Elongated Dodecahedron (angol nyelven). Wolfram MathWorld
• Weisstein, Eric W.: Pyritohedron (angol nyelven). Wolfram MathWorld
• Stellation of Pyritohedron VRML models and animations of Pyritohedron and its stellations.
• Richard Klitzing: 3D convex uniform polyhedra (angolul)
• Editable printable net of a dodecahedron with interactive 3D view
• The Uniform Polyhedra
• Origami Polyhedra – Models made with Modular Origami
• Dodecahedron – 3-d model that works in your browser
• Virtual Reality Polyhedra The Encyclopedia of Polyhedra
  • VRML models
  1. Regular dodecahedron regular
  2. Rhombic dodecahedron quasiregular
  3. Decagonal prism vertex-transitive
  4. Pentagonal antiprism vertex-transitive
  5. Hexagonal dipyramid face-transitive
  6. Triakis tetrahedron face-transitive
  7. hexagonal trapezohedron face-transitive
  8. Pentagonal cupola regular faces
• K.J.M. MacLean, A Geometric Analysis of the Five Platonic Solids and Other Semi-Regular Polyhedra
• Dodecahedron 3D Visualization
• Stella: Polyhedron Navigator: Software used to create some of the images on this page.