Ikozaéder

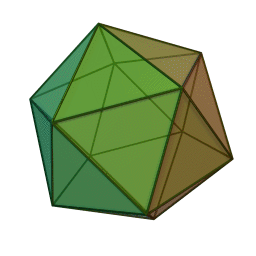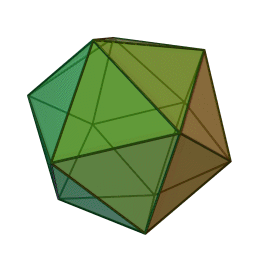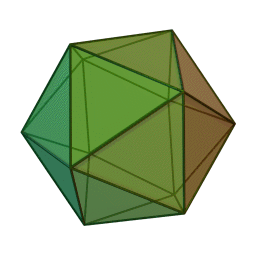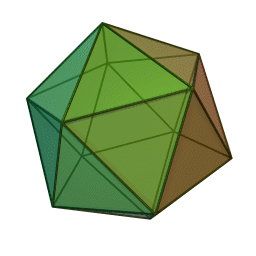
Az ikozaéder (ógörög: εἰκοσάεδρον, eikosáedron; eikoszi = húsz, hedron = ülés) olyan poliéder, melynek húsz lapja van.

Az „ikozaéder” szó alatt gyakran a szabályos ikozaédert értik, mely az öt platóni vagy szabályos test egyike. Konvex, szabályos poliéder, melyet húsz háromszöglap alkot – ezekből a csúcsokon öt-öt találkozik. Tizenkettő csúcsa és harminc éle van. Duális poliédere a dodekaéder.

Szimmetriái[szerkesztés]

Mivel minden csúcsa, éle és lapja szimmetriával átvihető egymásba, ezért a platóni szabályos testek egyike. Szimmetriái:

Hat ötfogású forgástengely (a szemben levő csúcsain át)
Tíz háromfogású szimmetriatengely (a szemben fekvő lapjainak középpontján át)
Tizenöt kétfogású szimmetriatengely (a szemben levő éleinek felezőpontjain át)
Tizenöt szimmetriasíkja (a szemben levő éleinek közös felezőmerőlegese)
Középpontosan szimmetrikus a középpontjára

Szimmetriacsoportja duális teste, a dodekaéder nevén ismert dodekaédercsoport, 120 elemmel. Ebben a forgatások 60 elemű részcsoportot alkotnak, ami a legkisebb nem Abel egyszerű csoport, és a legnagyobb nem Abel normálosztó az összes szimmetria csoportjában. Az ikozaéder szimmetriacsoportja izomorf az ötelemű halmazok páros permutációinak csoportjával. Ez a nem kommutatív csoport egyszerű, és az egyetlen nem triviális normálosztó az ötelemű halmaz permutációinak csoportjában (azaz az ötödfokú szimmetrikus csoportban). Mivel az általános ötödfokú egyenlet Galois-csoportja izomorf az ötödfokú szimmetrikus csoportjával, ezért az általános ötödfokú egyenlet nem oldható meg gyökjelekkel. Az Abel–Ruffini-tétel bizonyítása ezt az egyszerű tényt használja, és Felix Christian Klein könyvet írt, amiben az ikozaéder szimmetriáinak elméletét használta, hogy analitikus megoldást adjon az ötödfokú egyenletre. A könyv 1884-ben jelent meg Vorlesungen über das Ikoksaeder und die Auflösung der Gleichungen vom fünften Grade (Előadások az ikozaéderről és az ötödfokú egyenletek megoldásáról) címmel^[1].

Mivel szimmetriáiban szerepel az ötös szám, ezért ez a csoport összeegyeztethetetlen a hézagmentes térkitöltéssel, így nincs ilyen szimmetriájú kristályrács. A kvázikristályokban azonban előfordulnak ikozaéder alakú cellák.

Az ikozaéder háromféleképpen színezhető uniform színezéssel. Ezek az 11213, 11212, 11111 számokkal reprezentálhatók, ahol a számok azt jelölik, hogy az egy csúcs körüli lapok milyen színűek lesznek.

Az ikozaéder a tetraéder snubjaként is előáll. Az így keletkezett ikozaéder mutatja az ikozaéder királis tetraéderes szimmetriáját. Oktaéderből alternált csonkolással is konstruálható, ez pyritoéderes szimmetriát mutat. A pyritoéderes szimmetriája egy nem szabályos ikozaédertípusnak is megvan, amit pszeudoikozaédernek neveznek, és aminek 8 szabályos és 12 egyenlő szárú lapja van. Duális teste a pyritoéder.

Név	Szabályos ikozaéder	Snub oktaéder	Snub tetratetraéder	Ötszög alapú csavart bipiramis
Schläfli-szimbólum	{3,5}	s{3,4}	sr{3,3}
Wythoff-szimbólum	5 \| 3 2		\| 3 3 2
Szimmetria	I_h [5,3] (*532)	T_h [3⁺,4] (3*2)	T [3,3]⁺ (332)	D_5d [2⁺,10] (2*5)
Szimmetriarend	60	24	12	10
Uniform színezés	(11111)	(11212)	(11213)	(11122)&(22222)

Méretek[szerkesztés]

Ha egy szabályos ikozaéder élhossza $a$ , a köré rajzolt gömb sugara (amely az ikozaéder minden csúcsát érinti):

r_{u}={\frac {a}{2}}{\sqrt {\tau {\sqrt {5}}}}={\frac {a}{4}}{\sqrt {10+2{\sqrt {5}}}}\approx 0,9510565163\cdot a

és a beírt gömb sugara pedig (amely az ikozaéder minden lapját érinti)

r_{i}={\frac {\tau ^{2}a}{2{\sqrt {3}}}}={\frac {a}{12}}{\sqrt {3}}\left(3+{\sqrt {5}}\right)\approx 0,7557613141\cdot a

a középsugár (midradius), amely minden él közepét érinti

r_{m}={\frac {a\tau }{2}}={\frac {1}{4}}\left(1+{\sqrt {5}}\right)a\approx 0,80901699\cdot a

ahol $\tau$ (vagy φ) az aranymetszés.

Felszín és térfogat[szerkesztés]

Az a élhosszú szabályos ikozaéder felszíne (A) és térfogata (V) az alábbiak szerint számolható:

A=5{\sqrt {3}}a^{2}\approx 8,66025404a^{2}

V={\frac {5}{12}}(3+{\sqrt {5}})a^{3}\approx 2,18169499a^{3}

Koordináták[szerkesztés]

Az origó központú, 2 élhosszúságú ikozaéder csúcsait az alábbi Descartes-koordináták határozzák meg:

(0,\pm 1,\pm \phi )

(\pm 1,\pm \phi ,0)

(\pm \phi ,0,\pm 1)

,

ahol $\scriptstyle \phi ={\tfrac {1+{\sqrt {5}}}{2}}\approx 1,618$ az aranymetszés arányszáma (fi-szám).

Az egységnyi élű ikozaéder lapközéppontjait összekötve kapott dodekaéder élhossza $\scriptstyle {\tfrac {{\sqrt {5}}-1}{2}}\approx 0,618$ , ami az arany arány reciproka.

Az ikozaéder csúcsai gömbi koordinátákkal, szélességgel és hosszúsággal is megadhatók. Ha az északi és a déli sark az ikozaéder két csúcsa, akkor a többi tíz csúcs szélessége $\scriptstyle \pm \arctan {\tfrac {1}{2}}\approx \pm 26,57^{\circ }$ . Hosszúságok szerint egyenletesen oszlanak el, 36 fokonként.

Ez azt mutatja, hogy az ikozaéder ötszög alapú csavart nyújtott bipiramis D_5d diéderszimmetriával, azaz két szabályos ötszög alapú gúla összekapcsolva egy ötszög alapú antiprizmával.

Mértani arányok[szerkesztés]

Az ikozaéder egyedülálló a szabályos testek közül abban, hogy lapszöge nagyobb 120°-nál: ez az érték körülbelül 138,19°.

A szabályos hatszögek nem lehetnek egy szabályos poliéder lapjai, mert szögei 120°-osak, és nem fér el teljesszögnél kisebb szögben három 120°-os szög. Hasonlóan, az ikozaéder nem lehet egy négydimenziós szabályos test lapja, mert lapszöge nagyobb 120°-nál, és magasabb dimenzióban is minden csúcsban legalább három lapnak kell találkoznia.

Kisebb lapszögű szabályos testekkel együtt határolhat félig szabályos testeket. Ebben is hasonlít a hatszöghöz, ami szintén lehet félig szabályos test lapja. Végül határolhat négydimenziós konkáv szabályos testeket.

Ikozaéder kontra dodekaéder[szerkesztés]

Ha egy ikozaédert rajzolunk egy gömb belsejébe, az a gömb térfogatának kisebb részét (60,54%) foglalja el, mint egy ugyanabba a gömbbe írt dodekaéder (66,49%).

Az ikozaéder csonkítási sora:

Kép	Ikozaéder	Csonkított ikozaéder	Ikozidodekaéder	Csonkított dodekaéder	Dodekaéder
Coxeter-Dynkin diagram

Az ikozaéder és a dodekaéder segítségével további testek is alkothatók, amelyeknek ugyanazok a szimmetriáik, mint ezeknek a testeknek:

A rombotriakontaédernek 20 + 12 = 32 éle és 30 rombusz lapja van. Megkapható alkalmas méretű, közös középpontú ikozaéder és dodekaéder uniójának konvex burkaként.
Az ikozaédercsillag az ikozaéder éleinek meghosszabbításából keletkező konkáv test.

Az uniform ikozaéderes poliéderek családja
Szimmetria: [5,3], (*532)							[5,3]⁺, (532)

{5,3}	t{5,3}	r{5,3}	2t{5,3}=t{3,5}	2r{5,3}={3,5}	rr{5,3}	tr{5,3}	sr{5,3}
Duális testek

V5.5.5	V3.10.10	V3.5.3.5	V5.6.6	V3.3.3.3.3	V3.4.5.4	V4.6.10	V3.3.3.3.5

Kapcsolatai más testekkel[szerkesztés]

Az oktaéder 12 élét fel lehet osztani az aranymetszés szerint úgy, hogy az eredményül kapott csúcsok szabályos ikozaédert adjanak. Ezt úgy tehetjük, hogy vektorokat helyezünk az oktaéder éleire úgy, hogy minden lapot egy kör határol és ehhez hasonlóan minden élt az aranymetszés szerint felosztunk a vektor iránya mentén. Egy adott ikozaédert meghatározó öt oktaéder mindig szabályos összetett poliédert alkot.

Az ikozaéder élei közül kiválasztható három szemben fekvő élpár, hogy ezek három, egymásra páronként merőleges téglalapot feszítsenek ki, amely téglalapok oldalainak aránya éppen az aranymetszés, mivel az oldalak és az átlók szabályos ötszögeket alkotnak. Az ikozaéder így beírható egy kockába úgy, hogy ez a hat él a kocka hat oldalán feküdjön, és a kocka éleivel párhuzamos legyen.

A maradék 24 él 8 szabályos háromszöget határol, amelyek egy, az ikozaéder köré írt oktaéder lapjain fekszenek. Az ikozaéder csúcsai az oktaéder élein vannak.

Összesen öt ilyen helyzet van, amiben az ikozaéder minden éle élpárok egy ilyen halmazához tartozik, míg minden lap kétszer kerül egy köréírt oktaéder egy lapjára. Így hat az ikozaéder szimmetriacsoportja az öt helyzet 5!/2 = 60 páros permutációjára.

Az ikozaéder élei 12 szabályos ötszöget határoznak meg, minden él kettő és minden csúcs öt ilyen ötszöghöz tartozik. Ez a tulajdonság drótmodell építéséhez is használható.

Snub tetraéderként szintén megjelenik a tetraéderes és az oktaéderes szimmetriájú poliéderek családjában:

Az uniform tetraéderes poliéderek családja
Szimmetria: tetraéderes [3,3], (*332)							[3,3]⁺, (332)

{3,3}	t{3,3}	r{3,3}	t{3,3}	{3,3}	rr{3,3}	tr{3,3}	sr{3,3}
Duális testek

V3.3.3	V3.6.6	V3.3.3.3	V3.6.6	V3.3.3	V3.4.3.4	V4.6.6	V3.3.3.3.3

Uniform oktaéderes poliéderek
Szimmetria: oktaéderes [4,3], (*432)							[4,3]⁺ (432)	[1⁺,4,3] = [3,3] (*332)		[3⁺,4] (3*2)
{4,3}	t{4,3}	r{4,3} r{3^1,1}	t{3,4} t{3^1,1}	{3,4} {3^1,1}	rr{4,3} s₂{3,4}	tr{4,3}	sr{4,3}	h{4,3} {3,3}	h₂{4,3} t{3,3}	s{4,3} s{3^1,1}

Az uniform poliéderek duálisai
V4³	V3.8²	V(3.4)²	V4.6²	V3⁴	V3.4³	V4.6.8	V3⁴.4	V3³	V3.6²	V3⁵

Az ikozaéder a {3,n} Shläfli-szimbólummal jellemezhető poliéderek és parkettázások sorozatába is beletartozik:

Véges				Euklideszi	kompakt hiperbolikus				Parakompakt
{3,2}	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,9}	...	(3,∞)

Az ikozaéder, mint snub tetraéder az (3.3.3.3.n) csúcsalakzatú snub poliéderek és parkettázások sorozatába tartozik. Mindezek az alakzatok és duálisaik (n32) forgásszimmetrikusak, ahol n=6 az euklideszi síkon, és n > 6 a hiperbolikus síkon. Ezeket a sorozatokat n=2-től kezdik.

Schläfli

A *3.3.3.3.n* snub poliéderek és parketták családja
Symmetry n32 [n,3]⁺	Szférikus				Euklideszi	Hiperbolikus
Symmetry n32 [n,3]⁺	232 [2,3]⁺ D₃	332 [3,3]⁺ T	432 [4,3]⁺ O	532 [5,3]⁺ I	632 [6,3]⁺ P6	732 [7,3]⁺	832 [8,3]⁺	∞32 [∞,3]⁺
Snub alakzat	3.3.3.3.2	3.3.3.3.3	3.3.3.3.4	3.3.3.3.5	3.3.3.3.6	3.3.3.3.7	3.3.3.3.8	3.3.3.3.∞
sr{2,3}	sr{3,3}	sr{4,3}	sr{5,3}	sr{6,3}	sr{7,3}	sr{8,3}	sr{∞,3}
Snub duális alakzat	V3.3.3.3.2	V3.3.3.3.3	V3.3.3.3.4	V3.3.3.3.5	V3.3.3.3.6	V3.3.3.3.7	V3.3.3.3.8	V3.3.3.3.∞

Szférikus		Hiperbolikus parketták
{2,5}	{3,5}	{4,5}	{5,5}	{6,5}	{7,5}	{8,5}	...	{∞,5}

Az ikozaéder csúcsainak elrendezése megegyezik a Kepler–Poinsot-poliéderekkel. A nagy ikozaédernek az élelrendezése is megegyezik.

Kép	Nagy dodekaéder	Kis csillagikozaéder	Nagy ikozaéder

A hiperbolikus tér átfedés nélkül kitölthető egybevágó ikozaéder cellákkal, ahol egy él mentén három, egy csúcsnál 12 ikozaéder találkozik, és Schläfli-szimbóluma {3,5,3}. Ez a hiperbolikus tér négy szabályos cellarácsa közül az egyik.

A hiperbolikus tér ikozaéderes cellarácsa az ikozaéderekkel jelezve. A modell középpontjában található ikozaéder is látható

Merőleges vetületei[szerkesztés]

Az ikozaédernek három speciális vetülete van: lapközepes, élközepes és csúcsközepes.

Ortogonális vetítések
Közép	Lap	Él	Csúcs
Coxeter-sík	A₂	A₃	H₃
Gráf
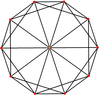
Projektív szimmetria	[6]	[2]	[10]
Gráf	Lap normális	Él normális	Csúcs normális

További rokon testek[szerkesztés]

A The Fifty-Nine Icosahedra szerint az ikozaédernek 59 csillagpoliédere van, ezek közül az egyik maga az ikozaéder, egy másik a szabályos Kepler–Poinsot poliéder. Három közülük szabályos összetett poliéder.^[2] Az ikozaéder lapsíkjai által kimetszett tartományok síkmetszete:

További tények[szerkesztés]

Az ikozaéder különböző testhálóinak száma 43 380, csak úgy, mint duálisának, a dodekaédernek.
Az ikozaéder lapjai három színnel színezhetők úgy, hogy két szomszédos lapnak ne legyen ugyanaz a színe. Ez a tetraédert kivéve minden konvex testre igaz, aminek háromszöglapjai vannak. Ez a Brooks-tételből következik, ha azt a test duális gráfjára alkalmazzuk.
Egy ókori görög probléma azt a kérdést veti fel, hogy melyiknek nagyobb a térfogata: egy adott gömbbe írt ikozaédernek, vagy az ugyanabba a gömbbe írt dodekaédernek. A feladatot többen is megoldották, köztük Hérón, Papposz és Fibonacci.^[3] Arra a következtetésre jutottak, hogy a gömb térfogatának nagyobb részét teszi ki a dodekaéder (66,49%), mint az ikozaéder (60,54%).^[4]
A pergamomi Apollóniosz arra a meglepő következtetésre jutott, hogy a két test térfogata úgy aránylik egymáshoz, ahogy a testek felszíne.^[5] Mindkét test képletében szerepel az arany arány, de más hatványon.^[6]

Gráfként[szerkesztés]

Az ikozaédergráf az a gráf, ami megkapható úgy, hogy csúcsai egy ikozaéder csúcsai, élei pedig az ikozaéder élei. A poliéder szimmetriatulajdonságai a gráfban is megjelennek, így az távolságtranzitív, távolságreguláris és szimmetrikus. Automorfiacsoportja megegyezik az ikozaéder szimmetriacsoportjával, így 120 elemű. Csúcsai 4, élei 5 színnel színezhetők, és átmérője 3.^[7]

Mint minden konvex poliéder gráfja, az ikozaéder gráfja is síkba rajzolható. Hamilton-gráf, azaz van egy köre, ami minden csúcsát tartalmazza.

Egy 3D gráf szerkezetet ír le az Almássy-féle ikozaéder.

Konstrukció egyenlő szögű egyenesekkel[szerkesztés]

Ikozaéder H₃ Coxeter-sík	6-ortoplex D₆ Coxeter-sík
Ez a konstrukció geometriailag azt jelenti, hogy egy 6-ortoplex 12 csúcsát levetítjük 3 dimenzióba. Ez reprezentálja D₆ geometriai hajtogatását a H₃ Coxeter-csoportba: A 2 dimenziós ábrákon a Coxeter-síkok ortogonális vetületei láthatók, ahol a két egymást fedő középponti csúcs határozza meg a leképezés harmadik tengelyét.

Egyes megközelítések a $\scriptstyle \mathbb {Q} \left[{\sqrt {5}}\right]$ számtestben végeznek számításokat. Itt azonban egy olyan konstrukciót mutatunk be, ami mellőzi ezt.

Az ikozaéder létezését arra vezetjük vissza, hogy létezik hat egyenes $\scriptstyle \mathbb {R} ^{3}$ -ben úgy, hogy bármely kettő közülük azonos szöget zár be. Egy, a közös metszéspontjukba helyezett középpontú gömb egy szabályos ikozaéder húsz csúcsát metszi ki.

Az egyenlő szögű egyenesek konstrukciójához ebből a mátrixból indulunk ki:

A=\left({\begin{array}{crrrrr}0&1&1&1&1&1\\1&0&1&-1&-1&1\\1&1&0&1&-1&-1\\1&-1&1&0&1&-1\\1&-1&-1&1&0&1\\1&1&-1&-1&1&0\end{array}}\right).

Némi számolással megmutatható, hogy A² = 5I, ahol I a 6×6-os egységmátrix. Ebből következik, hogy A sajátértékei $\scriptstyle -{\sqrt {5}}$ és $\scriptstyle {\sqrt {5}}$ , mindkettő 3 multiplicitással, mivel A szimmetrikus, és nyoma 0.

Tehát $\scriptstyle A+{\sqrt {5}}I$ euklideszi struktúrát indukál a $\scriptstyle \mathbb {R} ^{6}/\ker(A+{\sqrt {5}}I)$ hányadostéren, ami izomorf $\scriptstyle \mathbb {R} ^{3}$ -nel, hiszen $\scriptstyle {A+{\sqrt {5}}I}$ magja, $\scriptstyle \ker(A+{\sqrt {5}}I)$ három dimenziós. $\scriptstyle \mathbb {R} ^{6}$ -ban a hat koordinátatengely, $\scriptstyle \mathbb {R} v_{1},\dots ,\mathbb {R} v_{6}$ képe $\scriptstyle \pi :\mathbb {R} ^{6}\longrightarrow \mathbb {R} ^{6}/\ker(A+{\sqrt {5}}I)$ szerint hat egyenlő szögű egyenest ad $\scriptstyle \mathbb {R} ^{3}$ -ben, melyeknek páronkénti szöge $\scriptstyle {\arccos }{\tfrac {1}{\sqrt {5}}}$ . A ±v₁, ..., ±v₆ vektorok vetülete A $\scriptstyle {\sqrt {5}}$ sajátalterében egy ikozaéder csúcsait határozza meg.

Egy másik konstrukció az A₅ csoport reprezentációelméletét felhasználva vizsgálja ennek a csoportnak a hatását az ikozaéder szimmetriáira.

Előfordulás és alkalmazás[szerkesztés]

Biológia[szerkesztés]

Sok vírus fehérjeburka (ún. kapszidja), például a herpeszé ikozahedrális szerkezetű. Ezt a szerkezetet lehet a legkönnyebben felépíteni azonos fehérjemolekulákból alkotott részegységekből. A szabályos testek közül az ikozaéder térfogata a legnagyobb a felszínéhez képest.^[8]

Egyes baktériumok tartalmaznak ikozaéder alakú sejtszervecskéket.^[9] Az ikozaéder héj boríthat enzimeket és köztes termékeket is. Ezek a burkok különböző BMC tartományokat tartalmazó fehérjékből épülhetnek fel.

1904-ben Ernst Haeckel több sugárállatkáról írt, amelyek váza ikozaéderes szerkezetű.

Kémia[szerkesztés]

A klozo-karboránok alakja megközelítően ikozaéder. Az ikozaéderes ikresedés kristályokban és nanorészecskék között is előfordul.

Sok borid és a bór egyes allotrop módosulatában is B₁₂ az alap szerkezeti egység.

Fizika[szerkesztés]

Arany nanorészecskék elektronmikroszkópos képe

Ha az ikozaéder minden élére teszünk egy 1 ohmos ellenállást, akkor a szemközti csúcsok közötti ellenállás 0,5 ohm lesz, és a szomszédos csúcsok közötti ellenállás 11/30 ohm.^[10]

Az ikozaéder fontos szerephez jut a klasztereknél. Egy klaszter 3 - 50 000 atomból áll. A hétnél több atomos klasztereknél megjelenik egy ikozaéderre emlékeztető szerkezet. Ennek oka Friedel törvénye, ami kimondja, hogy minden szerkezet a lehető legkevesebb energiát tartalmazza, amiben a legközelebbi szomszédok közötti kötések száma maximális. Sok szabad szerkezetnél ez hétatomos mérettől jelentkezik, de vannak alóla kivételek, amelyek más szerkezeteket részesítenek előnyben, például a kockát.

Továbbá a klaszterfizikában vannak bűvös számok, amelyek szorosan kapcsolódnak a Mackay-ikozaéderhez. Az elektronszerkezethez hasonlóan ezek a számok egy réteg lezárását jelzik, így az ennyi atomból létrejött klaszterek különösen stabilak. Ezek a bűvös számok: 1, 13, 55, 147, 309, 561, 923 és 1415. Alan Mackaynek ez a korai észrevétele központi fontosságúvá vált a modern klaszterfizikában.^[11]

A klaszterszámok ezzel a képlettel számíthatók:

$C=\,{\frac {10n^{3}-15n^{2}+11n-3}{3}}$

ahol C a klaszterben levő összes atom száma, és n az egy élen levő atomok száma.

Játékok[szerkesztés]

A szerepjátékok gyakori kelléke a húsz oldalú dobókocka. Az egyes akciók véletlenszerű kimenetelének meghatározására használják. Számozása lehet 0-tól 9-ig úgy, hogy minden szám kétszer szerepel (K10), de a legtöbb modern kiadást 1-től 20-ig számozzák (K20).
Az Icosagame játékot ikozaéder alakú táblán játsszák. A játék korábban Ico Crystal Game néven volt ismert.
A Scattergories táblás játékban ikozaédert használnak betűválasztásra. Hat, az angol nyelvben ritkán használt betű nem szerepel, mint például az X, a Q és a Z.
A Vecsei Róbert és Zoltán által szabadalmaztatott Dogic egy türelemjáték, egy csavargatható ikozaéder.

Egy Magic 8 Ball belsejében egy ikozaéderre vannak felírva a lehetséges válaszok.

Egyebek[szerkesztés]

Rudolf von Laban ikozaédert használt térharmóniatanához, így erős hatással volt a modern táncra. Ezt ma a modern Laban-mozgástanulmányok viszik tovább.
Stafford Beer kibernetikai menedzsmentelméletében az ikozaéder szerkezet az ideális csapat tagjai közötti kapcsolatokat modellezi.
A német meteorológiai szolgálat GME időjárás-előrejelző modelljének rácsstruktúrájának magja egy földgolyóba írt ikozaéder csúcsai.
R. Buckminster Fuller és a japán Sodzsi Szadao ikozaéder alakú földgömböt tervezett. Ez a Fuller-vetítéssel ábrázolja a földgömböt, és maximális torzítása 2%.

A "Sol de la Flor" húsz panelből áll, amelyek egy ikozaéder csúcsaiban találkoznak. Ezeket a pontokat rozetták díszítik, amelyek a frangipáni virágát mintázzák.
A TDK Corporation logója egy olyan alakzatot tartalmaz, amely az ikozaéder csillagdiagramján alapul.
A Grundy Television ausztrál tévétársaság ikozaédert használt logóként.

Jegyzetek[szerkesztés]

↑ Felix Klein: Vorlesungen über das Ikosaeder und die Auflösung der Gleichungen vom fünften Grade. (németül) Lipcse: Teubner. 1884. Hozzáférés: 2022. október 14.
↑ Coxeter, Harold Scott MacDonald; Du Val, P. & Flather, H.T. et al. (1999), The Fifty-Nine Icosahedra (3rd ed.), Tarquin, ISBN 978-1-899618-32-3 (1st Edn University of Toronto (1938))
↑ Herz-Fischler, Roger (2013), A Mathematical History of the Golden Number, Courier Dover Publications, pp. 138–140, ISBN 9780486152325, <https://books.google.com/books?id=aYjXZJwLARQC&pg=PA138>.
↑ Buker, W. E. & Eggleton, R. B. (1969), "The Platonic Solids (Solution to problem E2053)", American Mathematical Monthly 76 (2): 192.
↑ Simmons, George F. (2007), Calculus Gems: Brief Lives and Memorable Mathematics, Mathematical Association of America, p. 50, ISBN 9780883855614, <https://books.google.com/books?id=3KOst4Mon90C&pg=PA50>.
↑ Sutton, Daud (2002), Platonic & Archimedean Solids, Wooden Books, Bloomsbury Publishing USA, p. 55, ISBN 9780802713865, <https://books.google.com/books?id=vgo7bTxDmIsC&pg=PA55>.
↑ Weisstein, Eric W.: Icosahedral Graph (angol nyelven). Wolfram MathWorld
↑ C. Michael Hogan. 2010. Virus. Encyclopedia of Earth. National Council for Science and the Environment. eds. S. Draggan and C. Cleveland
↑ Bobik, T.A. (2007), "Bacterial Microcompartments", Microbe (Am. Soc. Microbiol.) 2: 25–31, <http://www.microbemagazine.org/index.php/01-2007-home/2308-bacterial-microcompartments>. Hozzáférés ideje: 2012-02-22 Archivált másolat. [2013. július 29-i dátummal az eredetiből archiválva]. (Hozzáférés: 2014. február 20.)
↑ Klein, Douglas J. (2002). „Resistance-Distance Sum Rules” (PDF). Croatica Chemica Acta 75 (2), 633–649. o. [2007. június 10-i dátummal az eredetiből archiválva]. (Hozzáférés: 2014. február 15.)
↑ A. L. Mackay: A dense non-crystallographic packing of equal spheres. In: Acta Crystallographia. Band 15, 1962, S. 916–918, doi:10.1107/S0365110X6200239X

Források[szerkesztés]

A Wikimédia Commons tartalmaz Ikozaéder témájú médiaállományokat.

Angolul[szerkesztés]

Paper models of the icosahedron
The Uniform Polyhedra
K.J.M. MacLean, A Geometric Analysis of the Five Platonic Solids and Other Semi-Regular Polyhedra
Interactive Icosahedron model - works right in your web browser
Virtual Reality Polyhedra The Encyclopedia of Polyhedra
Tulane.edu A discussion of viral structure and the icosahedron (archív: 2008. február 23.)
Paper Models of Polyhedra Many links
Origami Polyhedra - Models made with Modular Origami
Printable Geometric Net of a Regular Icosahedron (archív: 2012. március 4.) Life is a Story Problem.org (archív: 2012. március 21.)
video of icosahedral mirror sculpture
Origami Polyhedra – Models made with Modular Origami

Németül[szerkesztés]

[1] Felix Klein: Vorlesungen über das Ikosaeder und die Auflösung der Gleichungen vom fünften Grade. (németül) Lipcse: Teubner. 1884. Hozzáférés: 2022. október 14.

[2] Coxeter, Harold Scott MacDonald; Du Val, P. & Flather, H.T. et al. (1999), The Fifty-Nine Icosahedra (3rd ed.), Tarquin, ISBN 978-1-899618-32-3 (1st Edn University of Toronto (1938))

[3] Herz-Fischler, Roger (2013), A Mathematical History of the Golden Number, Courier Dover Publications, pp. 138–140, ISBN 9780486152325, <https://books.google.com/books?id=aYjXZJwLARQC&pg=PA138>.

[4] Buker, W. E. & Eggleton, R. B. (1969), "The Platonic Solids (Solution to problem E2053)", American Mathematical Monthly 76 (2): 192.

[5] Simmons, George F. (2007), Calculus Gems: Brief Lives and Memorable Mathematics, Mathematical Association of America, p. 50, ISBN 9780883855614, <https://books.google.com/books?id=3KOst4Mon90C&pg=PA50>.

[6] Sutton, Daud (2002), Platonic & Archimedean Solids, Wooden Books, Bloomsbury Publishing USA, p. 55, ISBN 9780802713865, <https://books.google.com/books?id=vgo7bTxDmIsC&pg=PA55>.

[7] Weisstein, Eric W.: Icosahedral Graph (angol nyelven). Wolfram MathWorld

[8] C. Michael Hogan. 2010. Virus. Encyclopedia of Earth. National Council for Science and the Environment. eds. S. Draggan and C. Cleveland

[Bobik2007-9] Bobik, T.A. (2007), "Bacterial Microcompartments", Microbe (Am. Soc. Microbiol.) 2: 25–31, <http://www.microbemagazine.org/index.php/01-2007-home/2308-bacterial-microcompartments>. Hozzáférés ideje: 2012-02-22 Archivált másolat. [2013. július 29-i dátummal az eredetiből archiválva]. (Hozzáférés: 2014. február 20.)

[10] Klein, Douglas J. (2002). „Resistance-Distance Sum Rules” (PDF). Croatica Chemica Acta 75 (2), 633–649. o. [2007. június 10-i dátummal az eredetiből archiválva]. (Hozzáférés: 2014. február 15.)

[11] A. L. Mackay: A dense non-crystallographic packing of equal spheres. In: Acta Crystallographia. Band 15, 1962, S. 916–918, doi:10.1107/S0365110X6200239X

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]