Gúla

A gúla vagy piramis olyan geometriai test, amelynek alaplapja n oldalú sokszög, palástja pedig olyan háromszögekből áll, amelyeknek egy közös, nem az alaplap síkjába eső csúcsuk van, és az ezzel a csúccsal szemben levő oldalaik egyben az alapsokszög oldalai. A gúlákkal rokon testek a bipiramisok, amiket két, alapjuknál összeillesztett gúla alkot.
A gúla lapjainak és csúcsainak száma egyaránt n+1, ahol n az alap oldalainak száma. Éleinek száma 2n.
Képletek[szerkesztés]
A gúla térfogata: , ahol Ta a gúla alapterülete, h a gúla magassága.
A gúla felszíne: , ahol Ta a gúla alaplapjának területe, Tp pedig a gúla palástjának területe. A gúla palástjának területét az őt alkotó háromszögek területeinek összegeként kaphatjuk meg.
Egyenes gúla[szerkesztés]
Az egyenes gúla olyan gúla, aminek csúcspontja az alap szimmetriaközéppontja fölött van. (Ennek akkor van értelme, ha az alapsokszögnek van valamilyen forgásszimmetriája.) Más szóval, a csúcsot és az alap középpontját összekötő egyenes merőleges az alaplap síkjára. Az oldalélek hossza különböző lehet. Ha az alapsokszög nem forgásszimmetrikus, akkor nincs értelme egyenes gúláról beszélni, mivel egy háromszög alapú gúla csúcsa éppen a háromszög körül írt kör középpontja felett van. Ha a háromszög tompaszögű, akkor ez a háromszögön kívülre esik, ami ellentmond az egyenes szó alkalmazásának.
A szabályos gúla olyan egyenes gúla, aminek az alapja szabályos sokszög. A szabályos tetraéderek és a jól ismert négyzet alapú piramisforma is szabályos gúla.
A szabályos gúla felszíne: , ahol A az alap területe, k az alap kerülete és h a palást hossza (vagyis a palástot alkotó háromszög magassága, azaz a gúla oldalmagassága).
Súlypontja a magasságának az alaphoz közelebbi negyedelőpontja.
Ferde gúla[szerkesztés]
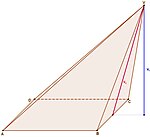
Egy szabályos sokszög alapú gúla ferde, ha:
- az élei nem egyforma hosszúak
- a magasság talppontja nem esik egybe az alap szimmetriaközéppontjával
- a csúcsot és az alap középpontját összekötő szakasz nem merőleges az alap síkjára
A talppont éppúgy lehet az alapon belül, mint kívül.
Tetraéderek[szerkesztés]
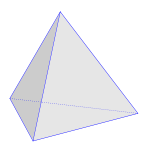
A tetraéderek éppen a háromszög alapú gúlák. A szabályos tetraéder minden éle egyenlő hosszú, oldallapjai egybevágó szabályos háromszögek. Az ortocentrikus tetraéderek szemben fekvő élei merőlegesek egymásra. Ezek a tetraéderek egy speciális csoportját alkotják, mert ezek pontosan azok a tetraéderek, melyeknek van magasságpontjuk (a tetraéder magasságpontját a háromszögekkel analóg módon definiáljuk). A többi tetraédernél a négy magasságegyenes nem metszi egymást egy pontban. A négy magasságvonal akkor és csak akkor metszi egymást egy pontban, ha a tetraéder szemközti élei páronként merőlegesek egymásra.
Szélsőértékek[szerkesztés]

A tetraéderek között az adott felszínhez tartozó maximális térfogatú test a szabályos tetraéder. Hasonlóan, a szabályos oktaéder is egy ilyen szélsőérték. A szabályos oktaéder összerakható két négyzet alapú gúlából, amiknek az oldallapjai szabályos háromszögek. Ehhez képest a szélsőértéket adó szabályos négyzetalapú gúla viszonylag hegyes.
Legyen egy ilyen gúla alapjának élhossza a. Ekkor a gúla magassága:
az oldallapok magassága:
a (maximális) térfogat:
A térfogatszámítás bizonyítása[szerkesztés]
Elemi geometriai bizonyítás[szerkesztés]
Az elemi geometriai bizonyítás három lépésből áll:
Két ugyanolyan alapterületű és egyforma magasságú gúla térfogata megegyezik. Ez a Cavalieri-elvvel és a középpontos hasonlóság tulajdonságaival bizonyítható.
A tetraéderek térfogata a képlettel számítható, hiszen egy háromszög alapú hasáb három egybevágó tetraéderre bontható.
A gúlákat tetraéderekre lehet bontani az alaplap háromszögelésével és a kapott csúcsokat a gúla csúcsával összekötve. A tetraéderek magassága megegyezik az eredeti gúla magasságával, alapjaik összterülete megegyezik az eredeti gúla alapterületével, így a képlet általánosan is igaz. Egy másik megokolás szerint van egy tetraéder, ami ugyanolyan alapterületű és magasságú, mint az eredeti gúla, így a térfogatuk is egyenlő.
Érdemes még megemlíteni, hogy a kocka három egybevágó négyzet alapú gúlára osztható, amiknek csúcsai a kocka csúcsaiban futnak össze.
Infinitezimális megokolás[szerkesztés]
Az y tengelyt a gúla csúcsa felé irányozzuk úgy, hogy a gúla magassága az y tengely egy darabja legyen. A gúlát végtelen sok végtelenül finom rétegre bontjuk, és δ(y)-nal jelöljük az y-odik rétegben a gúlafelszínének vastagságát. Így a középpontos hasonlóság tulajdonságai alapján:
Ezzel egy réteg térfogata dV = δ(y)dy. Innen a gúla térfogata a rétegek térfogatainak összegzésével kapható meg:
Csonkagúla[szerkesztés]
Ha a gúlát egy, az alappal párhuzamos síkkal elvágjuk egy kisebb gúlát és egy csonkagúlát kapunk.
A csonkagúla térfogata: , ahol T1 és T2 az alaplapok területe, H a csonkagúla magassága.
Források[szerkesztés]
- Reimann István: Geometria
- (angolul) Weisstein, Eric W. "Pyramid." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Pyramid.html













![{\displaystyle {\frac {A}{m^{2}}}\cdot {\frac {1}{3}}\left[y^{3}\right]_{0}^{m}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d19e5c7956bdbff223e077acc1ffa8df5489bec)
![{\displaystyle {\frac {A}{m^{2}}}\cdot {\frac {1}{3}}\left[m^{3}-0\right]={\frac {1}{3}}A\cdot m}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5da392f2dca22b9d9b7267ff3ce016cba6390a45)
