A matematikafilozófia története
- Ez a szócikk 1931-ig, Gödel nevezetes tételeinek megjelenéséig tárgyalja a matematikafilozófiát. A mai irányzatokra vonatkozóan lásd: matematikafilozófia.
A matematikafilozófia története azokat az eseményeket, elméleteket öleli fel, melyek a matematikáról mint tudományról való gondolkodással kapcsolatosak, vagyis hogy vajon a különböző korokban hogyan vélekedtek a matematikáról, milyen kép élt e tudományról (főképp, de nem kizárólag művelői, a matematikusok elméjében). A matematikafilozófia története nem a matematika története, hanem alapvetően a matematika tudományfilozófiájának, a matematikában felmerülő filozófiai kérdéseknek a története. Vannak olyan matematikatörténeti események, melyek nem játszanak fontos szerepet ebben a tekintetben és a matematikafilozófiai elméletek sincsenek mindig jelentős hatással magára a matematikára.
Az ókor matematikafilozófiája[szerkesztés]
A folyammenti kultúrák matematikaképe[szerkesztés]
A korai civilizációk matematikai megállapításai elsősorban a technika fejlődésének velejárójaként, mint tapasztalati törvények jelentek meg. Az építészet történetének homályába vész a derékszög-szerkesztés azon módjának eredete, hogy 3, 4 és 5 egység hosszúságú köteleket kell kifeszíteni háromszög alakban, eképp az 5 hosszúságú kötéllel szemközti szög derékszög. A kör kerületének az átmérőjéhez való viszonyszámára közelítő törteket írtak fel, melyek egyik generációról a másikra hagyományozódtak.
Egyiptomban a szögletes testek térfogatának kiszámítását egyfajta átlagszámítással végezték el. Mind Egyiptomban, mind Mezopotámiában számítási eljárásokat dolgoztak ki a kevésbé egyszerűbb törtmennyiségekkel végzett számítások és a magasabbrendű műveletek megkönnyítésére.

Az elméleti jellegű kérdések inkább szöveges feladatokban megfogalmazott első- és másodfokú egyenletek megoldására vonatkoztak, melyekben sikereket értek el, bár általános módszerük nem volt az összes gyök megkeresésére.
A matematikai tárgyú történeti forrásokból arra következtethetünk, hogy az ősi kultúrák a matematikában nem törekedtek valamiféle teljes, vagy pontos megoldás megadására. Ez annak köszönhető, hogy a matematikára elsősorban mint alkalmazott tudományra tekintettek, melynek feladata a közgazdasági, építészeti, csillagászati (ill. tengerhajózási) számítások elvégzésének megkönnyítése volt. A teljes pontosság helyett az elég jó közelítés volt a céljuk, de semmiképpen sem egy esetleges megoldás teljes körű elméleti vizsgálata, körülbelül úgy, mint a mai numerikus matematika esetén. Ezt látszik alátámasztani az is, hogy az ezzel a hagyománnyal közvetlen kapcsolatban lévő indiai matematika például az arkusztangens függvény értékeit már a 14. században végtelen sor segítségével volt képes kiszámítani (bizonyos tekintetben érvényes gondolatmenettel, noha jellemző módon a mai értelemben vett bizonyítás nélkül).
Thalész és a korai püthagoreusok (Kr. e. 7–6. sz.)[szerkesztés]

A görög matematika, szemben az egyiptomival és a babilonival, elrugaszkodva az építészeti és közgazdaság-tudományi alkalmazásoktól, önálló tudománnyá fejlődött. A görög matematika első időszakában a geometria elsőbbséget élvezett az aritmetikával szemben, abban az értelemben, hogy a legtöbb aritmetikai fogalmat geometriaira vezettek vissza. Kialakult a matematikai tétel fogalma, mely egyfajta általánosságot kifejező matematikai kijelentés, szemben a tapasztalattal és az esetleges megállapításokkal. Amikor valaminek a létezését kívánták megmutatni, akkor azt főként elemi geometriai úton tették, mely eljárást szerkesztésnek, konstrukciónak neveztek. A szerkesztéshez csak körzőt és vonalzót használtak.[2] A tételek igazságának felismerési módja – a „belátás” és „megmutatás” – ábrák segítségével átélhető vizuális élmény, amely még nem a levezetés, de már az általánosság fennállásának gondolati úton történő igazolása volt. A geometriában ez ábrákkal, a számtanban kavicsokkal történt.

Thalész bizonyítási módszere a „kongruenciabizonyítás” volt, melynek alapelve az egybevágóság, illetve az átdarabolhatóság. Ezek lényegében véges, konstruktív (a gyakorlatban végrehajtható) bizonyítási eljárások. Síkgeometriai bizonyításait akár papírlappal, ollóval, az alakzatok kivágásával és egymásra helyezésével is elvégezhetnénk.
Az első időszak Püthagorasz iskolájának megjelenésével zárult le, és kezdetét vette az aritmetika korszaka. A püthagoreusok világképük alapjául a számokat választották. A világegyetem harmóniáját a számok tökéletességével kapcsolták össze. Aritmetikai szemléletre épülő matematikaképük akkor került válságba, amikor bebizonyosodott, hogy a négyzet átlójának és oldalának aránya nem fejezhető ki két egész szám hányadosaként, azaz nem aritmetikai fogalom. A megoldást az aritmetika újbóli geometrizálása jelentette, mely a knidoszi Eudoxosz megalkotta arányelméleten alapult.
A deduktív matematika hajnala (Kr. e. 6–4. sz.)[szerkesztés]

Az eleai filozófia, Parmenidész és az eleai Zénón hatására megjelent az igény a deduktív bizonyításra. Filozófiai okokból az indirekt bizonyítást tekintették az igazság egyedüli kifejezési módjának. A legkorábbi deduktív értekezés Eukleidész Elemeinek a párosról és páratlanról írt részének keletkezése, melyet feltehetően még a püthagoreusok alkottak. Az absztrakt bizonyítás módszerének hatékony alkalmazása vezetett el ahhoz a felismeréshez, hogy a négyzetgyök kettő nem racionális szám (inkommenzurábilis arány). A számfogalom biztos alapra helyezése végett ebben az időben keletkezett Eudoxosz arányelmélete, mely később történeti alapját képezte Dedekind, a valós számok halmazelméleti definíciójára vonatkozó kutatásainak. A deduktív matematika és a logika kezdetei tehát összekapcsolódnak a görög matematika újbóli geometrizálódásával.

Platón ideatana adott először magyarázatot a matematikafilozófia egyik legfontosabb kérdésére, mégpedig hogy miből ered a matematikai tételek nagy fokú objektivitása. Platón szerint „árnyékvilágban” élünk, tárgyaink, fogalmaink nem valóságosak. A valóságos létezők az ideák világában keresendők. Amikor geometriai alakzatokról fogalmazunk meg tételeket, akkor valójában felfedezzük az ideális világ, ideális alakzatainak tulajdonságait. A matematikai fogalmak ideáinak létezéséből következik, hogy minden ember ugyanazokat a matematikai kijelentéseket tekintheti csak igaznak. Platón ezzel a gondolattal megalapozta azt a filozófiai álláspontot, melyet a 21. században a jelentés referenciális elméletének, vagy metafizikai realizmusnak nevezünk. Ennek matematikai válfaja a matematikai realizmus, melyre gyakran hivatkoznak úgy, mint platonizmus, ami rendkívül erős elmélet, habár kritikusainak ellenérvei sem gyengébbek.
Eukleidész és kora (Kr. e. 4. sz.)[szerkesztés]

A matematikai tudást rendszerezett formában tankönyvekbe foglalták, melyek címe Elemek (ti. a geometria és az aritmetika tudományának elemei) volt. Az egyetlen fennmaradt ilyen összefoglaló mű Eukleidész Elemek c. könyve (feltehetőleg azért, mert ez volt a legjobb, így ez volt a legnagyobb példányszámú). A deduktív tárgyalásmód hármas talapzaton nyugodott: definíciók, posztulátumok és axiómák. Az axiómák olyan állítások, melyeket a korban evidensnek tartottak, a posztulátumok ezzel szemben egyesek által vitatott, de Eukleidész által „megkövetelt” kiinduló állítások voltak. Eukleidész idejére a konstruktív módszer (ábrák és szerkesztés) egyensúlyba került az indirekt bizonyítással (redukció ad abszurdum – visszavezetés a lehetetlenre). Például mind a Thalész-tételt, mind a Pitagorasz-tételt átdarabolással (vagy átdarabolásra visszavezethető módon) igazolták, mely bizonyításban nagy szerepet kapott az ábra. Megfordításukat viszont indirekt látták be, amely a logika nem csekély ismeretéről árulkodik. Erre a korszakra vezethető vissza a klasszikus logika azon álláspontja, mely szerint valamely matematikai objektum létét úgy is lehet igazolni, hogy mutatunk rá példát, de úgy is, hogy nem létezésének feltételezéséből ellentmondásra jutunk. Ekkor foglalja össze Arisztotelész az Organonban a klasszikus logika alapelveit, és mutat rá annak korlátaira.
Késői görög matematika (Kr. e. 4. sz. – Kr. u. 4. sz.)[szerkesztés]

Arkhimédész fizikai szemlélettel állt hozzá a tételek felismeréséhez. Ezzel ő volt a heurisztikus módszer (és Pólya György heurisztikájának) előfutára, a felfedezés és intuíció fontosságát hangsúlyozta. Olyan intuitív és újszerű gondolatokkal közelített a geometriához, ami nem cáfolt rá feltaláló mivoltára. A szakaszokban emelőket, a háromszögek középpontjában súlypontot látott. A görbevonalú síkidomok területét annak végtelen sok végtelenül keskeny sávra bontásával számította ki. Ugyanezt a pergai Apollóniosz végtelen közelítő mértani összeggel határozta meg.
Papposz matematikatörténeti művet írt. Összefoglalta a matematika módszertanát, amelyben lényeges szerepet szánt a heurisztikának. Megfogalmazta a párhuzamossági axióma (Eukleidész V. posztulátumának) egy átfogalmazását. Célja – mint sok elődjének – az volt, hogy az ötödiket megpróbálja levezetni az első négy posztulátumból. Ezenkívül Papposz rámutatott arra, hogy a matematikai tételeknek mindig meg kell vizsgálni a megfordításukat. Akkor jutunk ugyanis előbbre a tétel megértésében, ha megismerjük egyrészt minden lényeges következményét, másrészt mindent amiből következik. A leghasznosabb a tétel megértésében viszont az, ha minél több ekvivalens megfogalmazására bukkanunk. Ezzel Papposz a matematikai kijelentések jelentésének egyfajta – nem feltétlenül platonista (mai elnevezéssel verifikacionista) – meghatározását adta.
Az újkor matematikafilozófusai (16–18. sz.)[szerkesztés]
Galilei az eukleidészihez hasonló módon rendezte deduktív rendszerbe a kinematikáról írt művét. Felfedezte a végtelennel kapcsolatos, már Zénónnál is megjelenő paradoxont, ami szerint „a rész egyenlő az egésszel”. Ez a felismerés a 19. században Cantornál jött elő újra, mint a végtelenség definíciója. Galilei úgy tartotta, hogy a matematika a természet nyelve.
Descartes megírta Értekezések a módszerről című könyvét, amelyben megfogalmazta a tudományos kutatás máig érvényes kritikus alapállását. Eszerint:
- Semmit ne fogadjunk el igaznak, míg annak igaz, vagy evidens voltáról meg nem győződünk. Ne tegyünk elhamarkodott tudományos kijelentéseket.
- A kutatás tárgyát annyi gondolati egységre osszuk, ahányra csak lehet, az alapos és kimerítő tárgyalás érdekében.
- Az érvelésnek rendszerezettnek kell lennie. A felépítésnek az egyszerűbb fogalmaktól az összetettebbekig kell haladnia.
- Mindenütt teljes felsorolásra, általános kijelentések megfogalmazására törekedjünk.

Descartes mindazonáltal már a Módszerről geometriai részében sem vitte végig következetesen gondolatmenetét. Tárgyalásmódja nem volt deduktív, megállapításai nem levezetéssel, hanem esszészerű formában keletkeztek, diszkussziói, felsorolásai nem voltak teljesek. Ez azonban nem azt jelenti, hogy ne gondolta volna komolyan a kutatás módszerét, és az ne lenne ma is érvényes. Itt inkább az a furcsa kettősség mutatkozik meg, ami szinte mind a mai napig él a matematikában. Lakatos Imre rámutatott, hogy a tételek és bizonyítások evolúciószerűen fejlődnek a matematikus elméjében és a matematikatörténetben. A deduktív bizonyítás csak ennek végállapotát tükrözi és az érvényességet, igaz voltát biztosítja, de semmit nem mond a matematikai fogalmak értelméről, jelentéséről és fejlődéséről.
Spinoza volt az első, aki szétválasztotta a matematika filozófiáját a teológiától. A püthagoreus és platóni hagyomány a matematikát az isteni rend kifejeződéseként tekintette, mely szerint az isteni törvények következménye a matematikában található rend és objektivitás. Descartes és Leibniz megfordította a gondolatmenetet. Szerintük a matematika és a logika kétségbevonhatatlan tényei igazolni tudják Isten létét. Spinoza rámutatott arra, hogy a matematika objektivitása és kristálytisztasága nincs kapcsolatban a teológiai kérdésekkel. A tudománynak a teológiától és a tekintélyektől független módon kell kutatnia a természeti törvényeket.
Leibniz megpróbálta az arisztotelészi logikát formulákban kifejezni. Megalkotta a calculi universalist, illetve a lingua universalist, az „egyetemes nyelvet”, ami a tudományok általános leírására lett volna hivatott.
Kant a matematikát az a priori / a posteriori és analitikus/szintetikus dimenziókban helyezte el. Szerinte a matematika állításai szintetikus és a priori állítások. Szintetikusak, amennyiben igazságuk nem evidens, a bennük előforduló fogalmak immanens tulajdonsága, hanem belátásuk gondolati műveleteket (deduktív út) igényel; a prioriak, amennyiben nem a tapasztalat alapozza meg igazságukat, hanem a belső intuíció.
Modern matematikafilozófia a 19. században[szerkesztés]
A matematika módszertana a 19. század elején gyökeresen megváltozott. Újrafogalmazódtak a bizonyítással szemben támasztott követelmények, és a középkori felfogáshoz képest az axióma fogalma is lényeges jelentésváltozáson ment keresztül. Mindezek hatására kialakult a modern logika és a modern matematikafilozófia.

„A szigorúság forradalma”[szerkesztés]
19. század közepén (az 1850-es, 60-as évekre) – főleg Cauchy és Weierstrass munkásságának köszönhetően – kialakult a bizonyítások olyan szigorú elemzésének módja, mint amelyet ma is tapasztalunk, ha kinyitunk egy felsőbb szintű matematikáról szóló könyvet. A bizonyításelemzés szigorúbbá válásának szükségszerű velejárója a rejtett előfeltevések kimutatása és a matematikai fogalmak definícióinak pontosítása volt. Lényegében ennek, a matematikára azóta is jellemző pontosságnak a megjelenését nevezzük (Lakatos Imre kifejezését használva) a szigorúság forradalmának. Néhány pontban áttekintjük, hogy miért vált szükségessé ez.
Ellenpéldák az analízisben[szerkesztés]
A 17. században létrejött differenciál- és integrálszámítás (közös nevén analízis, régebben „infinitezimálszámítás”) rendkívül hatékony módszernek mutatkozott a fizikában. Az égi mechanika 18. századi diadalában az analízis is osztozott. Segítségével percre pontosan előre lehetett jelezni a bolygók, holdak és üstökösök mozgását.

Az analízis a matematika komoly alapágává vált. Éppen ezért volt meglepő, mikor később sorra felbukkantak olyan ellenpéldák, amik az analízis általános tételeinek érvényességét látszottak szűkíteni. (Ilyen volt például Abelnek (1826) a folytonos függvények konvergens sorozatáról szóló tételhez gyártott ellenpéldája.) Sokan – a legnevesebb matematikusok, az analízis „nagy öregjei” közül is – úgy gondolták, hogy ezek hajuknál előrángatott dolgok, puszta agyszülemények, amik a matematika valóságára nincsenek hatással. Természetesen ezen a ponton a tudományos diskurzus megszűnne, de voltak, akik komolyan vették a cáfolatokat, és megpróbáltak a bizonyítások mélyére tekinteni, hogy felleljék a hibákat vagy pontatlanságokat. Végül ez utóbbi (a tudományosabb) vélemény hívei győzedelmeskedtek.
Megjegyzés: Nem kell azt gondolnunk, hogy az analízis tételeit ugyanazok a matematikusok, akik a számelméletben nagy pontossággal tevékenykedtek, elhanyagolták. A pontatlanság oka nem a kor matematikusaiban keresendő. Az aritmetika sokkal biztosabb fogalmi háttérre épült, mint a végtelen kicsiny és végtelen nagy számok intuitív fogalmát használó analízis. A természetes számok kavicsmodellje sokkal ellenőrizhetőbb kép, mint a végtelen kicsiny mennyiségek intuitív képe. Mindazonáltal tény, hogy az intuitív gondolkodás sikere az analízisben megrészegíthette a kutatókat. Ahogy D'Alembert mondta: „Előre a felfedezés útján! Az igazolást majd az utókor elvégzi.” Az ilyen úttörők meglepetésére, az utókor több esetben nem az igazolást, hanem a cáfolást végezte el – ha nem is az eredmények helytelenségét, de az érvelések támadhatóságát leleplezve.

Bizonytalanságok a geometriában[szerkesztés]
Kiderült, hogy az ellenpéldák felbukkanása nem korlátozódik az analízisre. Az Euler-féle poliédertételre is találtak cáfoló szituációt. Galois (1829) nemszerkeszthetőségi tételei rámutattak arra, hogy az irracionális számok elméletének megalapozása sem geometriailag, sem aritmetikailag nincs jól kivitelezve. Ha ugyanis nem szerkeszthető meg minden irracionális szám hosszúságú szakasz az egyenesen, akkor mik az irracionális számok?
A „paralellák problémájának” megoldása is váratott magára, mely a párhuzamossági axiómának a többi eukleidészi axiómából történő levezetését tűzte ki célul. Korszakalkotó meglátása a kérdésben Bolyai Jánosnak (1832) támadt. Akár ellentmondásra vezet a párhuzamossági axióma tagadása, akár nem, a geometria számára biztos alap a párhuzamossági axiómát mellőző, maradék axiómarendszer (feltéve, hogy az euklideszi geometria ellentmondásmentes, bár ezt a korban a szemléletből adódóan evidenciának tartották). A „biztonságos” maradék axiómarendszerben felépített geometriát nevezte Bolyai abszolút geometriának. Felvetődik azonban a kérdés: léteznek-e egyáltalán ilyen nemeuklideszi geometriák?[3]
A matematika megalapozásának paradigmája[szerkesztés]
Miután a bizonyításelemzés módszerét sikerült megszigorítani, és az analízis alapfogalmait is visszavezették az aritmetikára (ezt nevezzük az analízis aritmetizálásának), megfogalmazódott az az igény, hogy a teljes matematikát biztos alapokra kell helyezni. Ezt az álláspontot nevezik a matematika megalapozási paradigmájának. Hatására létrejöttek a matematikában később matematika alapjai (metamatematika) néven összefoglalt tudományterületek. Feladata olyan egységes elmélet keresése lett, melynek keretein belül az egész matematika ellentmondásmentesen elhelyezhető. Természetesen a matematika alapjainak kutatása nem mentes a világnézeti (metafizikai, pragmatikai stb.) vonatkozásoktól, nézetektől. Ezért vitatható, hogy – legalábbis célkitűzéseit tekintve – teljesen matematikai természetű résztudománynak mondható-e. Mindazonáltal kétségtelen, hogy az ezen a területen dolgozó matematikusok tevékenységük során komoly eredményeket értek el. Elsőként Dedekindnek a valós számokkal kapcsolatos vizsgálatai voltak nagy jelentőségűek. Visszanyúlt Eukleidész arányelméletéhez, s az irracionális számok elméletét visszavezette az aritmetikára (1872, 1888).
Cantor megalkotta a halmazelméletet (1874), mely kiváló segédeszköznek bizonyult a végtelen halmazok, így a számok, a sík és a tér vizsgálatához. Cantor halmazelmélete – a később naiv halmazelméletnek nevezett elmélet – jó eséllyel pályázhatott a megalapozási paradigma hívei által áhított „szuperelmélet” helyére.
Megjegyzés: A megalapozási paradigma – melyet gyakran a kissé pejoratív csengésű fundacionalizmus (sőt: „fundamentalizmus”) elnevezéssel illetnek támadói –, sem napjainkban nem osztatlanul elfogadott elv, sem a 19. században nem volt az. Az antifundamentalisták például bizonyos metamatematikai tételekre hivatkozva lehetetlennek tartják, hogy a matematika egyetlen elméleten belül elhelyezhető legyen. Azonban tény, hogy a megalapozási elv régebben a matematikafilozófia fősodorbeli áramlatát jelentette, és ma is ez az elv húzódik meg a legtöbb matematikafilozófiai vizsgálódás hátterében.
Frege logicista programja[szerkesztés]
Cantor naiv halmazelmélete lényegében tisztán logikai fogalmakra épül (mint például a predikátum és igazságtartománya). Ha tehát Cantor halmazelméletének eszközeivel sikerül a matematikát leírni, akkor kijelenthetjük, hogy a matematika a logika része. Természetesen, amennyiben a logika szabályain kívül további előfeltevéseket kell tennünk, ahogyan ezt tesszük is az euklideszi geometria axiómáiban, akkor máris nem állíthatjuk, hogy a kérdéses elmélet tisztán logikai. Gottlob Frege volt az, aki megmutatta, hogy ha a geometriát nem is, de az aritmetikát ki lehet fejezni – a naiv halmazelmélet segítségével – tisztán logikai terminusokban, mindenféle matematikai természetű axióma feltételezése nélkül. Az olyan kezdeményezéseket, melyek a matematikát a logikára kívánják visszavezetni, logicista álláspontoknak nevezzük.
Az aritmetika logikai megalapozása[szerkesztés]
Frege álláspontját és kivitelezésének módját Az aritmetika alapjai című könyvében fejti ki. Alapgondolata a természetes számok definíciójára a mai átírásban a következő volt. A nullát úgy definiálta, mint az összes olyan halmaz halmaza, melynek nincs eleme. Természetesen van ilyen halmaz, mert például az {x|„x nem egyenlő x-szel”} halmaz üres (a jelölések értelmét lásd a naiv halmazelmélet szócikknél). Az 1-et úgy definiálta, mint az összes olyan halmaz halmaza, mely azonos számosságú egy egyelemű halmazzal. Egyelemű halmaz szintén létezik, mert mondjuk az {x|x=0} halmaz egyelemű. Hasonlóképpen definiálta az összes természetes számot egy induktív definíció segítségével. Frege volt az első, aki a természetes számokat halmazelméleti fogalmak segítségével definiálta.
A formalista ideológia elterjedése[szerkesztés]
Ha meg tudnánk kérdezni arról Fregét, hogy munkásságában mit ítél a legjelentősebb alkotásnak, akkor bizonyára az aritmetika logikai megalapozása lenne a válasz (ez a kérdés persze több szempontból is rossz). Az utókor mégis Frege logikában elért eredményeit méltányolja leginkább. Frege korszakalkotó módon megalkotta a formális logikát. Célja, hogy a rejtett lemmákat, ki nem mondott előfeltevéseket úgy mutassa ki, hogy a bizonyítást elemi következtetési lépések formális láncolataként írja le. Eközben csak olyan kifejezéseket szerepeltet, melyeket addig már definiált. Vegyük észre, hogy ez a program Descartes módszerének a végső határig feszített kivitelezése. Egy elméletet szavakra, mondatokra bont le és az elmélet értelmét és a mondatok igazságát ez alapján próbálja feltárni. Nem véletlen, hogy Fregét tartják az modern analitikus nyelvfilozófia megteremtőjének. Amennyiben sikerül a bizonyításokat ezen a formális matematikai nyelven leírni, akkor elérjük a teljes bizonyosságot, abban az értelemben, hogy a formalizáció során semmilyen megalapozatlan állítás felhasználására nem lesz módunk.

A matematika és a logika egyes részterületeinek formalizálására már korábban is tettek erőfeszítéseket. Leibniz az általa calculi universalisnak nevezett formális nyelvében megkísérelte formalizálni az arisztotelészi logikát (1714). George Boole formalizálta a kijelentéskalkulust, és adott hozzá egy algebrai, egy logikai, egy valószínűségelméleti és (tanítványa, Venn jóvoltából) egy geometriai interpretációt (1854). Úgy gondolta, hogy ezzel megteremtette a matematika egységes leírását. Később Peano formalizálta az aritmetikát[4] (1896). Munkája sokkal ismertebb volt, mint Fregéé, így Peano jelölésrendszere terjedt el. Mindazonáltal Frege rendszere sokkal általánosabb érvényű volt, filozófiai és logikai kidolgozottságát tekintve pedig messze Peano elmélete előtt járt. Frege műveire csak később, Russell hívta fel a figyelmet.
Peano, Frege és Russell hatására a megalapozási paradigma kibővült a formalista szemlélettel. A „szigorúság forradalma” által a bizonyításelemzésre rótt teher súlyát némiképp könnyítette, hogy az elfogadható érveléseket a formális logika összegyűjtötte. A bizonyítások formalizálásával azok helyességét elvileg „teljes bizonyossággal” megállapíthatjuk. Ezért a megalapozást megvalósító elmélet keresése valójában egy formális nyelvi megalapozó elmélet keresésévé alakult árt.
A megalapozási elv első válsága[szerkesztés]

A naiv halmazelmélet ellentmondásai gyorsan napvilágot láttak. Először Cantor szembesült ellentmondással (Cantor-antinómia), de ezt csak később, a Burali-Forti-antinómia napvilágra kerülése (1897) után publikálta. A Russell-antinómiát először Frege Az aritmetika alapjai II. című műve utószavából ismerhette meg a nagyközönség (1902). A matematikatörténet nevezetes pillanata volt, amikor Frege érzéseit a következő latin mondást idézve fejezte ki:
- „Solatium miseris, socius habuisse malorum.”
- [A szerencsétlenek vigasza, ha társuk akadt a bajban.]
A paradoxonok ugyanis Cantor, Dedekind és Russell eredményeire is negatív kihatással voltak. A megalapozási elv híveinek feladatává ezek után a paradoxonok kiigazítása vált.
Matematikafilozófia a 20. század első felében[szerkesztés]
A naiv halmazelmélet antinómiáinak feloldására számos elmélet készült, ezek közül három különösen fontos, mert irányadónak számít három markánsan különböző matematikafilozófiai áramlat számára.
Russell logicista programja[szerkesztés]
Russell azon kívül, hogy mentesíteni akarta Cantor elméletét az ellentmondásoktól, célul tűzte ki, hogy megmenti Frege logicista programját. Formális logikai elmélete, a típuselmélet és az elágaztatott típuselmélet számos addig fellépő logikai paradoxont kiküszöböl (így például a Russell-paradoxont és a definiálhatóság Grelling-Nelson-paradoxonát). Célja azonban ennél sokkal több volt. A Whiteheaddel közösen megírt Principia Mathematica című könyvében részletesen kifejti, hogy miként lehet a típuselméletben rekonstruálni a matematika alapjait, ezzel visszavezetve a matematikát a logikára. Meg kell azonban állapítani, hogy kísérlete korántsem tekinthető sikeresnek. Ahhoz, hogy akár csak a természetes számokat definiálni tudja a típuselméletben, fel kellett tennie az úgynevezett végtelenségi axiómát. Ezzel viszont pont egy olyan nemlogikai előfeltevést épített be rendszerébe, mely kétségessé teszi azt a kijelentést, hogy a matematikát tisztán a logika következményeként tekinthetjük.
A típuselmélet ugyan alkalmazásra talált a formális logikában, de mint a matematika alapjainak formális nyelvi megalapozása nem járt sikerrel. A matematikusok túl nehézkesnek találták a típusok rendszerét. Russell azonban sokkal nagyobb befolyásra tett szert a matematika filozófiájában. Nem kevéssé személyes tekintélyének köszönhetően szinte máig uralkodó az angolszász nyelvterületeken az a felfogás, miszerint a matematikafilozófia russelli tárgyalása az analitikus filozófia mintapéldája. A filozófia nem lehet más, mint a tudományok filozófiáinak összessége, a tudományfilozófiákat pedig az analitikus filozófia eszközeivel, a logikára alapozott nyelvfilozófia eszközeivel kell művelni. Ennek a legkönnyebben kivitelezhető esete a matematika filozófiája, hiszen a matematikában nyilvánul meg legtisztábban a helyes következtetés.

Az analitikus filozófia központi problémája a nyelvi elemek jelentésének feltárása. A logikára és a logikára visszavezetett, általa tiszta matematikának nevezett formális matematikára vonatkozóan a jelentés elmélete azonban elég kilátástalan képet fest. Russell szerint:
- „A tiszta matematikában sem azt nem tudjuk, hogy miről beszélünk, sem azt, hogy igazat mondunk-e vagy sem.”
Ugyanis a formuláknak önmagukban semmi kapcsolatuk a valósággal, a matematikában az axiómákat pedig önkényesen választjuk. Bár logicista programja nem tartható, mindamellett az analitikus filozófia alkalmazásával Russell a formalista-konvencionalista irányzat megteremtőjévé vált.
Hilbert finitizmusa[szerkesztés]

A halmazelmélet Zermelo–Fraenkel-axiómarenszerének sikeres bevezetése után nyilvánvalóvá vált, hogy jól működő módszer a matematikában a részterületek formális-axiomatikus elméletekké alakítása, azaz a formalizáció. Az axiómarendszerek „jóságának” kritériuma az, hogy ellentmondásmentesek és negációteljesek legyenek. Circulus vitiosushoz vezethet azonban belátni a halmazelmélet ellentmondásmentességét, ha halmazelméleti eszközökkel tesszük azt. Hilbert szerint olyan bizonyításokat kell használni, melyben a megengedett eszközök már biztos szemléleti alapon nyugszanak és nem feltételezik a végtelen számosságok végtelen hierarchiáját, melyeknek létét a korban sokan kritizálták. Hilbert a matematikai bizonyosság legelemibb, legkétségbevonhatatlanabb szintjeként a finit aritmetikát nevezte meg. A finit aritmetika olyan számelmélet, melyben számok semmilyen végtelen halmazára, mint totális egészre nem hivatkozunk. Ez lenne a biztos alap a matematika megalapozásához, illetve a ellentmondásmentességi bizonyítások elvégzéséhez. Kétséges volt azonban magának a Peano-aritmetikának is az ellentmondásmentessége. Több más jellegű problémával együtt ezen elmélet ellentmondásmentességi bizonyítását is feladatként fogalmazta meg a matematikustársadalom számára, az úgy nevezett Hilbert-program keretein belül.[5]
Ahogy Russell analitikus filozófiát csinált a matematikafilozófiából, úgy Hilbert, a matematikus matematikai princípiává kívánta tenni. Szerinte a matematika filozófiája a matematika formális rendszereinek matematikája, az általa metamatematika névvel illetett terület. Feladata az ellentmondásmentességi, a nemteljességi és a függetlenségi vizsgálatok elvégzése. Ugyanúgy, ahogy Russell típuselméletét sikerrel alkalmazta a formális logika, a metametematika tételei a matematikai logikának váltak komoly eredményeivé. Hilbert formalizmusa azonban különbözik Russell formalista-logicista irányvonalától. A matematika jelentését ugyanis Hilbert a finit matematikából kívánta származtatni, így egyáltalán nem gondolta jelentés nélkülinek. Finitista ideológiája azonban nem vált uralkodóvá, és formalista hozzáállását is sokan eredménytelennek ítélik.
Intuicionizmus, konstruktivizmus[szerkesztés]
Brouwer holland matematikus és filozófus elvetette a matematikafilozófia analitikus filozófiai szemléletét, és tagadta a formális nyelvi vizsgálatok matematikán belüli elsődlegességét. Szerinte a bizonyosság a „matematikai intuícióból” származik, melynek legalapvetőbb momentuma a természetes számok rákövetkezés útján történő keletkezése.
- „Az intuicionista matematika lényegében nyelv nélküli tevékenység, melynek eredete az idő elmozdulásának érzékelése, ti. annak, hogy egy életmozzanat két különböző dologra esik szét, melyek közül az egyik utat enged a másiknak, de megmarad az emlékezetben. Az így megőrzött kettősség a matematika alapintuíciója.” Brouwer
A természetes számok ezáltal egyfajta szüntelen keletkezés állapotában vannak, kizárva az intuicionista számára a totális (vagy aktuális) végtelen önállóan létezőként való elfogadását. Minden matematikai objektumot a természetes számokra kell visszavezetni, mégpedig úgy, hogy az illető objektumhoz véges sok lépésben eljuthassunk (konstrukciók). Az intuicionizmus nem fogadja el az indirekt egzisztenciabizonyításokat – vagyis az olyan bizonyításokat, melyek egy dolog létét azzal igazolják, hogy belátják: nemléte ellentmondásra vezet. Ekkor ugyanis nincs feltétlenül meg a közvetlen kapcsolat a természetes számokkal. Ebből viszont az is következik, hogy nem teljesülhet a Kizárt harmadik elve.
Időrendileg az intuicionizmus eszméje a hilberti finitizmus előtt született meg. Hermann Weyl, Hilbert tanítványa kacérkodott az intuicionista gondolat elfogadásával, ennek eredményeképpen jutott Hilbert arra az elhatározásra, hogy szükséges magának is kialakítania egy filozófiailag elfogadható, de a matematikai gyakorlathoz is jól illeszkedő matematikafilozófiát.
A konstruktivizmusnak volt az intuicionizmustól elkülöníthető „orosz” ága is, amelyet Andrej Markov vizsgálatai alapítottak meg. Alapfogalmai a Markov-algoritmus (normál algoritmus) és az erre alapozott „konstruálható objektum”-ok. Később több kiemelkedő matematikus a Szovjetunióban részben vagy teljesen Markov követőjévé lett, magukat konstruktivistáknak nevezve.[6]
A megalapozáselv második válsága[szerkesztés]
Miközben dúlt a szellemi harc az axiómarendszereket relativizáló hilberti és russelli formalizmus, illetve az emberi tényezőt is előtérbe hozó intuicionizmus között, aközben megszületett a modern matematikafilozófia egyik legnagyobb eredménye, Gödel első és második nemteljességi tétele (1931). Gödel tételei csapást mértek – bár nem egyértelmű, hogy mekkorát – mindenféle megalapozási elvre.
Az első tétel következményei[szerkesztés]
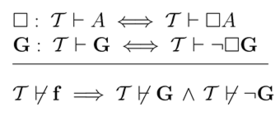
Gödel első nemteljességi tétele azt mondja ki, hogy:
- Minden ellentmondásmentes, a természetes számok elméletét tartalmazó, formális-axiomatikus elméletben megfogalmazható olyan mondat, mely se nem bizonyítható, se nem cáfolható.
Hilbert az aritmetika ellentmondásmentességének bizonyítását a matematikustársadalom számára feladatul tűzte ki. Hasonlóképpen elvárásai közé tartozott, hogy az aritmetikában minden állítás igazságát el tudjuk dönteni levezetéssel. Ezek az igények tehát azt jelentik, hogy:
- szükséges bebizonyítani, hogy hamis állítást nem vezethetünk le az aritmetika axiómarendszeréből (ellentmondásmentesség)
- legyen olyan axiómarendszere az aritmetikának, melynek nyelvén minden megfogalmazott kijelentés vagy igazolható vagy cáfolható (negációteljesség).
Gödel tétele szerint ez egyszerre nem teljesülhet, mert az aritmetika vagy ellentmondásmentes, vagy negációteljes. Sőt, minden nemtriviális axiomatikus elmélet esetén fennáll a bizonyosságnak eme hiánya. Durván fogalmazva: feltéve, hogy egy matematikai elmélet ellentmondásmentes, mindig megfogalmazható lesz benne olyan eldöntendő kérdés, melyre nem létezik válasz. Amennyiben a tételnek ezt az interpretálását elfogadjuk, az a matematika egy elég zavarbaejtő jellegére mutat rá.
A második tétel következményei[szerkesztés]
Gödel második nemteljességi tétele azt mondja ki, hogy:
- Ellentmondásmentes, a természetes számok elméletét tartalmazó, formális-axiomatikus elméletben az „ez az elmélet ellentmondásmentes” mondatnak megfelelő formális kijelentés nem bizonyítható.
A második tétel megítélésében centrális kérdés, hogy az „ez az elmélet ellentmondásmentes” aritmetikai kijelentésnek milyen jelentést tulajdonítunk. A következő – nem nyilvánvaló – értelmezés azonban sokkal súlyosabb következményekkel jár, mint az első tétel esetén.
- T ellentmondásmentességét nem lehet egy T-vel azonos, vagy gyengébb formális elméletben igazolni.

Tegyük fel, hogy a T formális-axiomatikus elmélet ellentmondásmentességét szándékozunk bizonyítani. Ezt a bizonyítást a T tárgyelmélet egy szintén formális-axiomatikus metaelméletében tesszük meg, például olymódon, hogy belátjuk egy konkrét S tárgynyelvi mondatra hogy ez nem bizonyítható T-ben (ez ugyanis elegendő T ellentmondásmentességéhez). Ha nem erősebb mint T, akkor megfogalmazható T-ben és kapjuk a formulát. Ha ebből következik , akkor rögtön ellentmondásra jutunk, hiszen Gödel második nemteljességi tétele szerint ekkor (lévén T ellentmondásmentes) .
Az aritmetikát minden megalapozási célra szánt matematikai elméletnek tartalmaznia kell, így ellentmondásmentességének bizonyítását eszerint nem lehet semmilyen azonos erősségű metaelmélet alapján bebizonyítani. Speciálisan: az aritmetika ellentmondásmentességét nem lehet aritmetikai eszközökkel bizonyítani – ahogy azt Hilbert szándékozott volna. (Megjegyezzük, hogy az aritmetika ellentmondásmentességére transzfinit bizonyítást azonban már talált Gerhard Gentzen 1936-ban.)
Ez a negatív eredmény sokkolta az addig a matematika megalapozásáról élénk diskurzust folytató matematikafilozófiával is foglalkozó matematikusokat. Jól illusztrálja a 20-as, 30-as évek hangulatát Neumann János, aki könyvében, miután hosszasan leírja a történteket, így összegez:
- „Azért meséltem el ennek a vitának a történetét ilyen részletesen, mert úgy hiszem, ennél jobban nem is lehetne óvatosságra inteni az embereket, nehogy túlságosan készpénznek vegyék a matematika rendíthetetlen szigorát. Mindez a mi korunkban történt, és magamról tudom, hogy ebben a korszakban az abszolút matematikai igazságról vallott saját nézeteim is milyen szégyenletes sebességgel változtak, volt, hogy egymás után háromszor is!”[7]
A mai matematikafilozófia áramlatairól lásd: matematikafilozófia.
Kapcsolódó szócikk[szerkesztés]
Jegyzetek[szerkesztés]
- ↑ Lásd még: Jahmesz egyiptomi írnok
- ↑ lásd: euklideszi szerkesztés
- ↑ A kérdéssel kapcsolatban lásd még: Frege geometriafilozófiája
- ↑ lásd Peano-aritmetika
- ↑ lásd Hilbert II. problémája
- ↑ Viktor Nyikolajevics Trosztnyikov: Konstruktív módszerek a matematikában. Stúdium könyvek 77., Gondolat, Bp., 1981. ISBN 963-280-980-7 .
- ↑ Neumann János: A matematikus. Idézett forrásmű 21. old.
Források[szerkesztés]
- Neumann János: A matematikus (1947). In: Neumann János: Válogatott előadások és tanulmányok. Szerk. Lukács Ernőné. Ford. Augusztinovics Mária. A fordítást az eredetivel egybevetette: Bródy András. Bp.: Közgazdasági és Jogi Könyvkiadó, 1965
- Bertrand Russell – Alfred North Whitehead: Principia mathematica, Cambridge, University Press, 1910 – elektronikus könyvtári formában itt
- K. Gödel: Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme, I. Monatshefte für Mathematik und Physik, 38 (elfogadva 1930. november 17., published 1931), pp. 173–198. in van Heijenoort: From Frege to Gödel. Harvard University Press, 1971
- Sain Márton: Matematikatörténeti ABC, Tankönyvkiadó, 1973
- Szabó Árpád: A görög matematika kibontakozása, Gondolat, 1978 (Gyorsuló idő)
- Euklidesz: Elemek, ford.: Mayer Gyula, Gondolat, 1983
- Lakatos Imre: Bizonyítások és cáfolatok, TypoTeX, Bp., 1998
- Kutrovátz Gábor: Lakatos Imre matematikafilozófiája
További információk[szerkesztés]
- John D. Barrow: A semmi könyve. A nulla kialakulásától a kvantumvákuumig; ford. Erdeős Zsuzsanna; Akkord, Bp., 2005 (Talentum tudományos könyvtár)







