Négyzetgyök
A matematikában a négyzetgyökvonás egy egyváltozós matematikai művelet, a négyzetre (második hatványra) emelés megfordítása (inverze). A gyökvonás azon esete, amikor .
Az szám négyzetgyökének jele:
A négyzetre emelés függvénye nem kölcsönösen egyértelmű leképezés, hiszen -nak és -nak ugyanúgy a négyzete. A négyzetgyökvonás művelete így nem lenne egyértelmű, emiatt a (valós) négyzetgyök definíciójakor kikötik, hogy az eredmény legyen nemnegatív.
A racionális törtkitevős hatványozás definíciójának segítségével a négyzetgyök úgy is írható, mint ½-dik hatvány:
A négyzetgyökvonás egy olyan művelet, ami átvezet a komplex számokhoz, mivel a negatív valós számoknak nincs valós négyzetgyökük. A racionális számok közül csak azoknak a négyzetgyöke lesz racionális, melyek felírhatók két négyzetszám hányadosaként. Így például a is irracionális, melyet már az ókorban bebizonyítottak.
A gyökjel a kis r betűből alakult ki, a jobb ág meghosszabbításával. A 16. században jelent meg. Eredetileg az r betűt a latin radix szó rövidítéseként a radikandus elé írták. Ha a radikandus bonyolultabb kifejezés volt, akkor zárójelbe tették. Így használta még Gauss is.
A négyzetgyök angol nevéből származik a sok programnyelvben használt sqrt jelölés.
Definíció a valós számok halmazán[szerkesztés]
Ha a nem negatív valós szám, akkor a négyzetgyökén azt a szintén nemnegatív számot értjük, aminek a négyzete a:
A valós számok halmazán negatív számokra nincs értelmezve a négyzetgyökvonás, hiszen bármely valós szám négyzete nemnegatív.
A valós négyzetgyökfüggvény[szerkesztés]


Azt a függvényt, ami a nemnegatív számokhoz a négyzetgyöküket rendeli, négyzetgyökfüggvénynek szoktuk nevezni:
Ekvivalensen, jelölje q azt a függvényt, ami a valós számokhoz a négyzetüket rendeli. Ha ezt leszűkítjük a nemnegatív számokra, akkor inverze a négyzetgyökfüggvény lesz:
A valós számokon értelmezett négyzetre emelés függvény nem injektív és nem szürjektív, így nem invertálható függvény. A nemnegatív számokon értelmezett négyzetre emelés függvény viszont invertálható, inverze a négyzetgyökfüggvény. Mivel a nemnegatív számokon értelmezett négyzetre emelés függvény értékkészlete csak nemnegatív számokat tartalmaz, azért a négyzetgyök csak ezekre a számokra értelmezhető. A korlátozás miatt a négyzetgyökfüggvény értékei sem negatívak. A négyzetre emelés függvénynek más invertálható korlátozásai is vannak, ám ezek inverzét nem tekintjük négyzetgyökfüggvénynek.
A négyzetgyökfüggvény a pozitív számok halmazán differenciálható, deriváltja
.
Nullában ellenben nincs deriváltja; a grafikon érintője itt függőleges.
Értelmezési tartományának minden zárt intervallumán Riemann-integrálható, és egy primitív függvénye
.
Tulajdonságai[szerkesztés]
- Mind értelmezési tartománya, mind értékkészlete a nemnegatív valós számok halmaza:
- Szigorúan monoton növekvő, azaz:
- Zérushelye: x=0
- Szélsőérték:
- Minimuma: x=0, f(x)=0
- Maximuma nincs
- Paritás szempontjából nem páros és nem páratlan, hiszen negatív számokra nincs is értelmezve.
Példák[szerkesztés]
| Radikandus | Négyzetgyök | Radikandus | Négyzetgyök | |
|---|---|---|---|---|
| 1 | 1 | 121 | 11 | |
| 4 | 2 | 144 | 12 | |
| 9 | 3 | 169 | 13 | |
| 16 | 4 | 196 | 14 | |
| 25 | 5 | 225 | 15 | |
| 36 | 6 | 256 | 16 | |
| 49 | 7 | 289 | 17 | |
| 64 | 8 | 324 | 18 | |
| 81 | 9 | 361 | 19 | |
| 100 | 10 | 400 | 20 |
Számolás négyzetgyökökkel[szerkesztés]
A négyzetgyökös kifejezésekkel való számolás tulajdonságai következnek a nem negatív valós számok négyzetének tulajdonságaiból:
- , ha
- , ha
- , mivel a négyzetgyökfüggvény szigorúan monoton nő.
- tetszőleges a valós számra.
- ellenben csak akkor teljesül, ha a nem negatív
A négyzetgyökvonással kapcsolatos problémák[szerkesztés]
- I.) Irracionális egyenletek:
Egyismeretlenes irracionális egyenleteknek nevezünk minden olyan algebrai egyenletet, ahol egyes algebrai kifejezések gyökjel alatt állnak.
- II.) Négyzetgyökvonás negatív valós számból:
Azokat a számokat, melyeket úgy kapunk, hogy egy valós negatív előjelű valós számból vonunk négyzetgyököt, imaginárius számoknak nevezzük. A komplex számok két fő részből tevődnek össze: egy képzetes (imaginárius) számból és egy valós számból.
Komplex négyzetgyökfüggvény[szerkesztés]

A komplex négyzetre emelés a valóshoz hasonlóan nem injektív; azonban a valós esettel ellentétben szürjektív, azaz minden komplex szám előáll négyzetként. Leszűkítéssel injektívvé tehető. Ennek inverz függvénye a négyzetgyökfüggvény egy ága, ami függ az adott leszűkítéstől.
A négyzetgyökfüggvény főértéke abból az ágból adódik, amit a
tartományra leszűkített négyzetre emelés definiál. Ez a leszűkítés már bijektív, és inverze, a négyzetgyökvonás főága az egész komplex számsíkon értelmezhető. Az egyetlen mellékág
A Descartes-koordinátákkal adott komplex szám esetén, ahol , valósak, a főérték
ahol a függvény értéke nempozitív esetén −1.
Polárkoordinátákkal a művelet egyszerűbben elvégezhető. Legyen a radikandus a komplex szám, melynek polárkoordinátás alakja
ahol és valósak úgy, hogy és ! Ekkor a főérték:
és a mellékérték ennek mínusz egyszerese:
A négyzetgyökök abszolútértéke a radikandus abszolútértékének négyzetgyöke. A főérték argumentuma a radikandus argumentumának fele. A mellékérték az origóra való tükrözéssel adódik. Ha komplex szám, akkor argumentuma az szög, ahol a pontok valós koordinátái az egy valós szám, a nulla valós szám és .
A komplex számokra nem teljesül az
- hatványtörvény, hogyha és . Ez megmutatható az esetben:
ahonnan az azonosság miatt
amire a negatív számok ellenpéldák. Ha például , akkor és miatt főértékének argumentuma , holott főértékének argumentuma .[1]
Mivel pozitív radikandusok esetén a főértéknek pozitívnak kell lennie, így a példa azt is megmutatja, hogy nem létezhet olyan komplex gyökfüggvény, amelyre a hatványtörvény teljesül. Azonban a hatványtörvény teljesül, ha a két oldalon nem kell egyezniük az előjeleknek. A következő képeken és a négyzetgyök argumentumát színezés jelöli.
- Komplex négyzetgyök
-
A négyzetgyök egyik ága
-
A négyzetgyök másik ága
-
A négyzetgyökfüggvény Riemann-felülete megmutatja, hogyan mennek át egymásba az ágak
Számítása[szerkesztés]
A valós és a komplex számok négyzetgyöke többféleképpen is kiszámítható.
Valós számok[szerkesztés]
Ha a szám nem írható fel két négyzetszám hányadosaként, akkor a négyzetgyöke irracionális még akkor is, ha a szám egész. Ennek kiszámítása azt jelenti, hogy tetszőleges pontossággal megközelíthető.
- Írásbeli gyökvonás: az írásbeli osztáshoz hasonló eljárás.
A szám jegyeit hátulról kezdve párokba osztja. Az első csoport adja a négyzetgyök első jegyét. A továbbiakban sorra figyelembe veszi a következő jegypárokat, és az (a + b)2 = a2 + 2ab + b2 azonosság alapján számol, ahol az a szám a már meglevő közelítés, és b a következő keresett számjegy.
- Intervallumok egymásba skatulyázása: könnyen érthető, de nehezen kivitelezhető módszer.
Példa: négyzetgyök kettő kiszámítása:
12 < 2 és 22 > 2 miatt az első jegy 1. 1,42 = 1,96 < 2 és 1,52 = 2,25 > 2, ezért a második jegy 4. Az eljárás hasonlóan folytatódik.
- Heron-eljárás vagy babilóniai módszer: a Newton-eljárás alkalmazása az x2 - a függvényre. Gyors konvergenciája miatt számológépek programozására használják.
- A négyzetgyökfüggvény 1 körüli Taylor-sorba fejthető a binomiális tétel szerint. A sor minden | x | < 1-re konvergens:
- CORDIC-algoritmus a gépi számításokhoz
- Grafikus módszer: a Pitagorasz-tételen alapszik
Az x számot felmérjük a számegyenesre, és Thalész-kört szerkesztünk a [0,x] szakaszra. 1-ben merőlegest állítunk a számegyesre; ez négyzetgyök x hosszú szakaszt metsz ki a körívből.
Komplex számok[szerkesztés]
Ha a valós és a képzetes részével van megadva, akkor a négyzetgyök főértéke
ahol sgn(y) a szignumfüggvény.
Az egyetlen mellékág a .
A polárkoordinátákban adott négyzetgyökei így számíthatók:
ahol n = 0 vagy 1. A főérték az n = 0 esetnek felel meg.
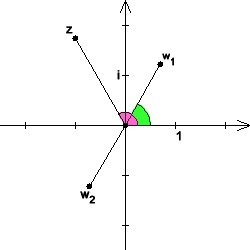
Geometriailag, a négyzetgyökök abszolútértéke megegyezik az adott komplex szám abszolútértékének négyzetgyökével, és a főérték argumentuma az adott komplex szám argumentumának fele. A másik érték ennek a középpontosan szimmetrikus párja.
Egy z komplex szám argumentuma az (1,0,z) irányított szög.
Példaként keressük a komplex szám négyzetgyökét. Ehhez kiszámítjuk az abszolútértékét:
Tehát a főérték
és a mellékérték
Négyzetgyökök a maradékosztály-gyűrűkben[szerkesztés]
Ha egy n természetes számra akkor a négyzetgyökvonás definiálható modulo n. A valós és a komplex esethez hasonlóan a maradékosztály-gyűrűben is értelmes kérdés, hogy van-e olyan q maradékosztály, ami négyzetre emelve az x maradékosztályt adja:
Az x maradékosztály négyzetgyökei modulo n kiszámíthatók így:
- Prímtényezős alakba írjuk az n számot
- Megoldjuk a kongruenciát a felbontásban szereplő minden prímhatványra
- Összevetjük ezeket a megoldásokat a kínai maradéktétel szerint.
Prímszám modulus[szerkesztés]
A prímhatványokról a kongruencia visszavezethető több prím modulusú kongruencia megoldására.
Egy prím modulusra általában nincs minden maradékosztálynak négyzetgyöke. Például modulo 3 és x=2 esetén a kongruencia nem oldható meg, mert nincs négyzetszám, ami hárommal osztva kettőt ad maradékul. Ezért, ha p>2, akkor először ezt a kérdést kell megvizsgálnunk.
A kérdést az
Legendre-szimbólum segít eldönteni, amire:
- .
Ha x kvadratikus nemmaradék, akkor nincs négyzetgyöke. Ha x és p nem relatív prímek, akkor a megoldás a nulla maradékosztály. Végül, ha x kvadratikus maradék, akkor két négyzetgyöke van. Ezzel az esettel foglalkozunk a továbbiakban.
- p négyes maradéka három
Az x kvadratikus maradék két négyzetgyöke
- p négyes maradéka egy
Az x kvadratikus maradék négyzetgyöke így számítható:
Választunk egy r számot, hogy:
legyen.
Rekurzívan kiszámítjuk ezt a sorozatot:
- .
Ekkor az x kvadratikus maradék négyzetgyökei:
Példa: Legyen és !
Ekkor a fenti képlet alapján a négyzetgyökök
Próbálgatással egy megfelelő érték , mivel:
A és értékekre adódik, hogy:
Behelyettesítéssel
Tehát 3 négyzetgyökei modulo 37 15 és 22 modulo 37.
Mátrixok négyzetgyökei[szerkesztés]
Ha négyzetes mátrix, akkor négyzetgyöke minden mátrix, melyet önmagával szorozva az mátrixot kapjuk:
A gyökvonás a többi esethez hasonlóan nem egyértelmű. Azonban, ha pozitív definit szimmetrikus mátrixok pozitív definit szimmetrikus gyökét keressük, akkor a válasz egyértelmű.
A négyzetgyök kiszámítása:
- A radikandust ortogonális mátrixszal diagonizáljuk (spektráltétel miatt lehetséges).
- Az átlós elemekből négyzetgyököt vonunk, mindig a pozitív értéket választva. Lásd: Cholesky-felbontás
- Visszatérünk az eredeti bázisba.
Az egyértelműség következik abból, hogy az exponenciális leképezés diffeomorfizmus a szimmetrikus mátrixok vektoterében a pozitív definit mátrixokra.
Integráloperátor közelítésének négyzetgyöke[szerkesztés]
Legyen integrálfüggvény, és legyen , ahol az pontokra és . Legyen továbbá függvény, és használjuk az közelítést! Példánkban a mátrix mérete :
Ez a művelet megismételhető, így kapjuk a kettős integrált:
így az mátrix felfogható numerikusan közelített integráloperátorként. Az mátrix nem diagonizálható, és Jordan-normálformája:
Ebből négyzetgyököt úgy lehet vonni, mint nem diagonizálható mátrixokból. De ebben a speciális esetben van közvetlenebb formális megoldás:
ahol , és .
Itt a diagonális indexe (a főátlóé nulla), és a kitevő . Hogyha behelyettesítjük a pozitív valós számot, így valós, és fdefiníciója alapján pozitív.
Így az „fél” határozott integrálja numerikusan közelíthető:
Hogyha keressük az összes olyan operátort, ami önmagával szorozva az közelítő integráloperátort adja, akkor be kell tenni a negatív előjelet, így a két megoldás .
A levezetéshez invertálni kell -t, azt eredményt a hatványra emelni, és újra invertálni.
Fordítás[szerkesztés]
Ez a szócikk részben vagy egészben a Quadratwurzel című német Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.
Jegyzetek[szerkesztés]
- ↑ Klaus Fritzsche. Tutorium Mathematik für Einsteiger. Springer-Verlag (2016)












![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)


























































![{\displaystyle {\begin{aligned}w_{1}&={\sqrt {\tfrac {2+(-1)}{2}}}+\mathrm {i} \cdot \operatorname {sgn^{+}} ({\sqrt {3}})\cdot {\sqrt {\tfrac {2-(-1)}{2}}}\\[0.3em]&={\sqrt {\tfrac {1}{2}}}+\mathrm {i} \cdot (+1)\cdot {\sqrt {\tfrac {3}{2}}}={\sqrt {2}}\cdot \left({\tfrac {1}{2}}+\mathrm {i} \cdot {\tfrac {1}{2}}{\sqrt {3}}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c65fbfa85729505faa6fa18dff479108b517c08c)















































