Szög



A szög mint síkgeometriai fogalom. A sík egy pontjából kiinduló két félegyenes a síkot két tartományra osztja. Az egyik tartomány és a két félegyenes szöget alkot. A szög jelentheti a félegyenesek által határolt síkrészeket (szögtartomány), illetve magukat a félegyeneseket is (a szög szárai, szögvonal). Azt, hogy a két szögtartomány közül melyikről van szó, a szárak közé rajzolt körívvel jelezzük. A félegyenesek közös pontját a szög csúcsának, a félegyeneseket a szög szárainak nevezzük. Szokták szögnek hívni a szögtartományt, és beszélnek forgásszögekről is, melyek forgatáskor keletkeznek, és a teljesszögnél is nagyobbak lehetnek. Forgásszögeknél szokás előjeles szögekről is beszélni. A pozitív előjel az óramutató járásával ellentétes forgásirányt jelöli.
A szög mint mennyiség. A síkszög arányszám: a szögcsúcs köré írt körvonalból a szög szárai által kimetszett ív hosszának és a hozzá tartozó sugár hosszának aránya. Ehhez hasonlóan a térszög is arányszám: a térszög csúcsa köré írt gömbfelületből a szög által kimetszett gömbfelület területének és a gömbsugárhossz négyzetének aránya. A térszögtől való megkülönböztetés miatt a síkbeli szöget síkszögnek is nevezzük. A síkszög mint mennyiség definiálható forgásszögként is, így lehet előjeles is, vagy a teljesszögnél nagyobb.
Definíciók[szerkesztés]


Alapvetően a szögnek kétféle definíció létezik: az előjel nélküli és az előjeles. A nem irányított szög előjel nélküli, az irányított előjeles. A bevezetésben említett definíció használatos például a koordináta-rendszerek és a koordináta-rendszer tengelyei esetén. A szög félegyenespárként való meghatározás esetén a félegyenesek egy közös pontból indulnak:
- Ha , egyenesek, amelyek az pontban metszik egymást, akkor az pont az , egyeneseket félegyenesekre osztja. Ekkor ezek a félegyenesek az ponttal együtt szöget alkotnak. Az pont a szög csúcsa, az , egyenesek pontból induló félegyenesei a szög szárai.
- A szög, pontosabban a szögtartomány a síknak az a része, melyet egy pontból kiinduló két félegyenes határol. Ezek a szögtartomány határa, míg a szögtartomány többi része a szög belseje.
Az iskolai tanítás során ezt a változatot használják, ezzel kiemelik azt, hogy a szögnek területe van. A belső, illetve a külső tér elhatárolásával a háromszög-geometria bevezetését szolgálja. A háromszög definiálható három szögtartomány metszeteként.
Az eddigi definíciók előjel nélküli szöget definiáltak. A következőkben előjeles szögeket is definiálunk.
Az is mondható, hogy a szög egy félegyenes végpontja körüli forgatásával keletkezik. Megkülönböztetésként ezt a szöget forgásszögnek is nevezik. A forgás irányára két lehetőség van:
- Balra forgatáskor az óramutató járásával ellentétes irányba forog
- Jobbra forgatáskor az óramutató járásával megegyező irányba forog
Az elforgatás (maga a folyamat és nem a végeredmény) lehet nagyobb is mint, a teljesszög. Az ilyen szög nagysága lehet nullától kisebb is és teljes szögtől, azaz 360°-tól illetve 2π radiántól nagyobb is (több, mint egy kör elforgatás). A szög fogalmának ily módon való kiterjesztése a trigonometrikus függvényeknél, a matematikai analízisben jelentős. A matematikában az óramutatóval ellentétes irány számít pozitívnak. Ha csak másként nem jelzik, akkor a forgatást ebbe az irányba végzik.
A geodéziában nem használnak előjelet, és a forgatás iránya mindig az óramutató járása szerinti. Az óra analógjára a szögeket 0-tól 24 h-ig, vagy 0 gontól 400 gonig mérik. Minden geodéziai műszert óramutató járása szerinti irányba forgatnak.
A szögek felosztása[szerkesztés]

- Nullszög: 0°.
- Hegyesszög: 0°-nál nagyobb, de 90°-nál kisebb szög.
- Gér: nyolcadkörívhez tartozó szög, 45°, π/4 radián.
- Derékszög: negyedkörívhez tartozó szög, 90°, π/2 radián. Mellékszögével egyenlő nagyságú.
- Tompaszög: 90°-nál nagyobb, de 180°-nál kisebb szög.
- Egyenesszög: félkörívhez tartozó szög, szárai egyenest alkotnak. Az egyenesszög két derékszög összege, 180°, π radián.
- Konvex szögek: az egyenesszögnél kisebb szögek, tehát a hegyesszögek, a tompaszögek és a derékszög konvex szögek.
- Konkáv szögek: más néven homorúszögek; az egyenesszögnél nagyobb szögek (az ábrán az ABC szög).
- Teljes szög: egész körívhez tartozó szög; a két szögszár egybeesik, és a belső tartománnyal együtt felöleli az egész síkot. 360°, 2π radián.
Jelölések[szerkesztés]


Az ISO 80000-2 szerint a szögeket a következőképpen adjuk meg:
- A szöget görög kisbetűkkel jelöljük, mint vagy .
- Az szöget két félegyenes, egyenes vagy él zárja közre. Irányát az irányából a irányába számítjuk.
- Három ponttal megadott szög esetén mindig a középső pont a szög csúcsa. Jelölése ABC szög, vagy . Ez a szög az és félegyenesek közé zárt szögek közül az, ami -re való matematikailag pozitív irányú forgatásával keletkezik.
- Az angol nyelvű szakirodalomban szokásos még a illetve jelölés.
A nem irányított szög jelölése »∠« (HTML ∠/∠, TeX \angle, Unicode U+2220). Irányított szög jelölésére használható még »∡« (HTML ∡/∡, TeX \measuredangle, U+2221). Mindkét jel megtalálható a Unicode-kódtáblában. A fekvő szög jelölés angol-amerikai; az Európában használt jel összetéveszthető az angol-amerikai »∢« U+2222 térszöget jelölő jellel. A szög és a meredekség jelölésére használható »∠« is.
Speciálisan, a derékszöget jelölik úgy is, mint:
- »∟«, derékszög alakban felrajzolva
- »⦝«, szög ívvel és ponttal
- »⊾«, szög ívvel
- »⦜«, szög négyzettel
- , ortogonális
Szögpárok[szerkesztés]

- Mellékszögek: két olyan szög, amelyeknek egy-egy szára azonos, a másik kettő pedig egyenest alkot. Egymást egyenesszöggé egészítik ki.
- Kiegészítő szögek: két olyan szög, amelyek összege egyenesszög.
- Pótszögek: két olyan szög, amelyek összege derékszög.
- Párhuzamos szárú szögek: Mint a neve is mondja, a száraik párhuzamos egyeneseken vannak. A párhuzamos szögek lehetnek:
- 1) egyállású szögek: A száraik páronként párhuzamosak és egyenlő irányításúak (egyenlő nagyságúak)
- 2) váltószögek: A száraik páronként párhuzamosak és ellenkező irányításúak (egyenlő nagyságúak)
- (speciális esetben) Csúcsszögek: csúcsuk azonos, és mindkét száruk egymás szárainak meghosszabbítása. Azonos nagyságúak
- 3) társszögek: A száraik páronként párhuzamosak és egyik pár egyező a másik ellenkező irányítású (egymás kiegészítőszögei)
- Merőleges szárú szögek: Mint a neve is mondja, a száraik egymásra merőleges egyeneseken vannak (egyenlő nagyságúak vagy egymás kiegészítőszögei)
További elnevezések[szerkesztés]

- Belső szög: egy sokszög szögpontjában találkozó két oldal által bezárt szög.
- Külső szög: egy sokszög szögpontjában találkozó oldal és a szomszédjának ama szögponton túl való meghosszabbítása által közbezárt szög.
A szögek mérése[szerkesztés]

 |
 |
A θ szög méréséhez egy körívet húzunk, melynek középpontja a szög csúcsa. Legyen a körív hossza s, a kör sugara pedig r, k pedig egy választott együttható. Ekkor a szög mértéke:
amely független a kör méretétől, mivel a körív és a sugár aránya állandó.
A szögeket dimenzió nélkülinek szokták tekinteni, mivel két hosszúság hányadosaként jelenik meg. Ennek ellenére a szögeket többféle mértékegységben fejezik ki attól függően, hogy milyen értéket választottunk a k együtthatónak.
- A fok, amelyet egy felső helyzetű körrel jelölnek (°), a teljes kör 1/360-ad része, tehát a teljes kör mértéke 360°. A fok 1/60-ad része az ívperc, melynek jelölése: ′ . Az ívperc 1/60-ad része az ívmásodperc, melynek jelölése: ″ A θ szög fokban való meghatározásához:
- Egy radián a mértéke annak a szögnek, amelynél a hozzá tartozó körív és sugár hányadosa 1. (vagyis k = 1 a fenti képletben). A teljes kör mértéke 2π radián. Egy radián 180/π fok, azaz közelítőleg 57,2958 fok. A radián rövidítése rad, de ezt jellemzően nem szokták kiírni a matematikai szövegekben, ahol az alapértelmezett mértékegység a radián. Ezt a választást az indokolja, hogy ezzel egyszerűbbek lesznek a képletek, és nem kerülnek bele mindenféle váltószámok. Lásd: [1] A radián a szögek mértékegysége az SI rendszerben.
- Léteznek más egységek is. Ezekről a Mértékegységek átszámítása#Szög tartalmaz adatokat.
| Szögmérték | Mértékegység | 1 teljesszög = | Mértékegység jele |
|---|---|---|---|
| – | Teljesszög | 1 | |
| Ívmérték | Radián | 2π | rad |
| Fok | Fok (perc, másodperc) | 360 | ° ( ′ ″ ) |
| Geodéziai szögmérték | Gradián (újfok) | 400 | gon (grad) |
| Időmérték | Óra, perc, másodperc | 24 | h m s |
| – | Tengerészeti vonás | 32 | ¯ |
| – | Tüzérzeti vonás | 6400 | mil ( A‰ ) |
| – | Százalék | nem lineáris | %, ‰ |
Síkszögek a térben[szerkesztés]

A térelemek által bezárt síkszögek is értelmezhetők.
- A párhuzamos egyenesek, síkok által bezárt szög a nullszög.
- Egy sík és az abban fekvő egyenes szöge is nullszög.
- Két metsző egyenes által bezárt szög a keletkezett szögek közül a kisebb, ami legfeljebb 90 fok.
- Két kitérő egyenes szöge megegyezik az eltoltjaik által bezárt szöggel.
- Egy metsző egyenes-sík pár szöge az egyenes és a síkra vett merőleges vetülete által bezárt szög.
- Két egymást metsző sík által meghatározott szög megegyezik azzal a szöggel, amit a síkban levő, a metszésvonalukra merőleges egyenesek bezárnak. Ezt a szöget nevezik lapszögnek.
Térszögek[szerkesztés]
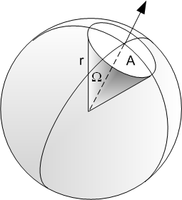
Térszög helyett térszögletet is mondanak. A térszögek nagyságát általában szteradiánban mérik, ami a radián térbeli megfelelője, de néha felbukkannak más mértékegységek is. Térszög található poliéderek csúcsánál. Lásd: Mértékegységek átszámítása#Térszög Egy szteradiánnyi szög a csúcsa köré írt r sugarú gömb felszínéből r2 területet metsz ki. A teljes gömbhöz tartozó térszög mértéke
-
Kanonikus térszög
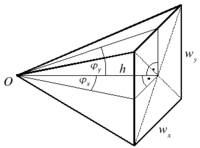
-
Egy gúla térszöge
Szögek különböző geometriákban[szerkesztés]
Többnyire euklideszi geometriáról lévén szó, a szögeket is euklideszinek tekintjük. Azonban más geometriákban is vannak szögek.
A háromszögek szögei és oldalai közötti kapcsolatokat egyenlőségek és egyenlőtlenségek írják le. A különböző geometriákban ezek az összefüggések különböznek. Euklideszi geometriában ismert összefüggés, hogy hosszabb oldallal szemben nagyobb szög van. Emellett a szinusztétel és a koszinusztétel pontos egyenlőséget is megad. A háromszögeket szögeik csak hasonlóság erejéig határozzák meg. A háromszögek szögeinek összege egyenesszög.
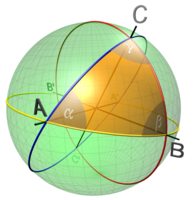
Gömbi geometriában a gömbi szinusztétel és a gömbi koszinusztétel érvényesül, illetve vannak még más tételek is. A háromszögeket szögeik egybevágóságig meghatározzák. A háromszögek szögeinek összege egyenesszögnél nagyobb.
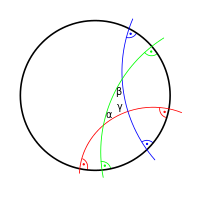
Hiperbolikus geometriában a hiperbolikus szinusztétel és a hiperbolikus koszinusztétel ad összefüggést. A háromszögeket szögeik egybevágóságig meghatározzák. A háromszögek szögeinek összege egyenesszögnél kisebb.
-
Gömbháromszög szögei
-
Háromszög szögei hiperbolikus geometriában
Szögek számítása[szerkesztés]
Derékszögű háromszög[szerkesztés]

Ha egy derékszögű háromszögben az egyik hegyesszög adott, akkor a másik egyértelműen meghatározott, mivel a szögek összege 180 fok, és ebben a derékszög kitesz 90 fokot, azért ha a hegyesszögek és , akkor .
Ha ismertek az , és oldalhosszak, akkor a hegyesszögek kiszámolhatók szögfüggvényekkel és árkuszfüggvényekkel. Ha a hegyesszögek és , akkor teljesül, hogy
Általános háromszög[szerkesztés]

Ha egy háromszög szögei , és , akkor . Ezért két szög meghatározza a harmadikat.
Ha ismert két oldal hossza és az egyikkel szemközti szög, akkor a másik oldallal szemközti szög szinusztétellel számítható. Teljesül például, hogy . Az árkusz szinusz függvénnyel .
Mindhárom oldal ismeretében a koszinusztétellel kiszámíthatók a szögek. Teljesül például, hogy . Az árkusz koszinusz függvénnyel .
Ha derékszögű koordináta-rendszerben a háromszög csúcsaival van megadva, akkor a belső szögek két vektor közötti szögként számíthatók. Legyenek a csúcsok , , ! Ekkor és az pontból kiinduló vektorok, így . Itt skaláris szorzat és a vektorok hossza.
Tetraéder szögei[szerkesztés]

A tetraéderben előforduló szögek:
- a lapokon, mint háromszögeken levő szögek
- a lapok lapszögei
- a csúcsoknál levő térszögek
Egyenesek hajlásszöge[szerkesztés]
Ha egy egyenes egyenlete egy sík derékszögű koordináta-rendszerében , akkor hajlásszögét az tengelyhez -val jelölve:
- .
Ez következik a tangens definíciójából. Az árkusz tangens használatával
- .
Ha a tangens nem létezik, akkor , ami azt jelenti, hogy az egyenes párhuzamos az tengellyel, így hajlásszöge az tengelyhez 0.
Két egyenes metszésszöge[szerkesztés]
Legyenek és egyenesek egy sík derékszögű koordináta-rendszerében a és pontokkal és és lineárisan független irányvektorokkal. Ha szögük , akkor
- .
Az egyenesek merőlegesek, ha metszésszögük derékszög, tehát . Ez ekvivalens azzal, hogy irányvektoraik skalárszorzata 0. Ez azt jelenti, hogy .[1]
Ha a két egyenes és alakban van megadva, és egymással bezárt szögük , akkor az általuk közrezárt szög az tengellyel bezárt hajlásszögekből számítható:
- .
Alkalmazva az addíciós tételt a tangensre:
- .
Mivel és , azért következik, hogy:
- .
Egybevetve
- .
Alkalmazva az árkusz tangenst kapjuk, hogy
- .
Az egyenesek pontosan akkor merőlegesek, ha . Ekkor az egyenletek nincsenek definiálva.[2]
Egyenes és sík metszésszöge[szerkesztés]
Legyen az irányvektorú egyenes és az normálvektorú sík metszésszöge. Ekkor
Két sík metszésszöge[szerkesztés]
Legyen és a két sík normálvektora! Ekkor a két sík metszésszöge
- .
Nevezetes szögek szerkesztése[szerkesztés]
Vannak szögek, amik megszerkeszthetők körzővel és vonalzóval. Ezek közül a legnevezetesebbek a derékszög, a 60, a 30 és a 72 fokos szögek, valamint az ezekből felezéssel, összeadással, kivonással kapható szögek. Az így keletkezett szögek mellett szerkeszthetők a szabályos 17-szögből kapható szögek is. Az algebra eredményei szerint a szögek általában nem harmadolhatók; nevezetesen, a 60 fokos szög nem harmadolható körzővel és vonalzóval.
Műveletek szögekkel[szerkesztés]
Szögek összeadása, kivonása[szerkesztés]
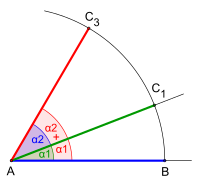
Összeadáskor úgy mérjük fel a szögeket, hogy körívet húzunk az első szögbe, amit meghosszabbítunk úgy, hogy a másik szög is odaférjen. Ezután a másik szögbe ugyanezzel a környílással körívet húzunk. A körív és a szög szárainak metszéspontjai közötti távolságot felmérjük az első szög melletti meghosszabbított körívre. Meghúzzuk a második szögszárat a csúcspontból a metszésponthoz.
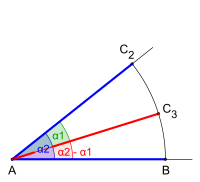
Kivonáskor hasonlóan járunk el. Úgy mérjük fel a szögeket, hogy körívet húzunk a nagyobb szögbe. Ezután a másik szögbe ugyanezzel a környílással körívet húzunk. A körív és a szög szárainak metszéspontjai közötti távolságot felmérjük a nagyobb szögtartományban befelé. Meghúzzuk a második szögszárat a csúcspontból a metszésponthoz. Így kapjuk a szögek különbségét.
Szögek felosztása[szerkesztés]

Szögfelezés: egy, a csúcsból húzott körívvel elmetsszük a szög két szárát, majd a kapott metszéspontokból ugyanakkora környílással köríveket húzunk úgy, hogy messék egymást. A szög csúcsát összekötjük a metszésponttal. Így elfeleztük a szöget.
Szögharmadolás euklideszi szerkesztéssel nem lehetséges, azonban közelítő szerkesztések lehetségesek. Továbbá vannak más eszközök is, például a Tomahawk rajzeszköz, melyek lehetővé teszik a szögharmadolást.
Tetszőleges arányú osztáshoz olyan segédeszköz kell, amivel szögek és szakaszok egymással arányosan egymásra képezhetők. Ilyen például egy arkhimédészi spirál vagy Hippiász-féle kvadratiksz. Így a szakaszok és a szögek felosztása kölcsönösen átvihetők egymásba. Ezek az eszközök használhatók olyan sokszögek megrajzolásához, melyek nem szerkeszthetők körzővel és vonalzóal.
A 60 fokos, és a belőle kapható szögek[szerkesztés]
60 fokos szög szerkesztése adott egyeneshez adott pontján át[szerkesztés]

Legyen az egyenes , és a pont !
- A pont körül kört húzunk, melynek metszéspontjait -gyel jelölje és .
- Ugyanezzel a sugárral kört vonunk az vagy a pont köré. Az első körrel vett egyik metszéspontot jelölje .
- A egyenes áthalad a ponton, és 60 fokos szöget zár be a egyenessel.
60 fokos szög szerkesztése adott egyeneshez adott külső ponton át[szerkesztés]

Legyen ismét az egyenes , és a pont !
- Merőlegest bocsátunk a pontból -re. Innen kapjuk az és kör-egyenes szimmetrikus metszéspontokat, a -vel átellenes pontot. A talppontot a továbbiakban jelöli.
- Kört húzunk körül úgy, hogy átmenjen a ponton. Ez a kör a továbbiakban .
- Ugyanekkora sugárral körül is kört húzunk, ez a kör. A két kör metszéspontjai és , melyek össztekötő egyenese a szakasz felezőmerőlegese.
- A háromszög egyenlő oldalú, melynek -n átmenő oldalai -et 60 fokban metszik.
Egy alternatív szerkesztésmód:
- Húzunk egy kört a pont körül úgy, hogy messe a egyenest. Az egyik metszéspontot megjelöljük, ez lesz az pont.
- Ugyanezzel a sugárral kört húzunk az pont körül, ennek egyik metszéspontja a pont.
- körül kört húzunk ugyanezzel a sugárral, ami a körüli kört a pontban metszi.
- A pont körül kört húzunk, ennek metszéspontja a pont körüli körrel a pont.
- A egyenes 60 fokban metszi a egyenest.
A 60 fokos szög szerkesztése[szerkesztés]

- Meghúzunk egy egyenes szakaszt
- Kijelölünk rajta egy O pontot
- Húzunk O-ból egy körívet, ami metszi az egyenes szakaszt; a metszéspont legyen A
- A körző szögnyílását változatlanul hagyva húzunk A-ból egy körívet, hogy messe az O középpontú körívet. Legyen ez a metszéspont B
- Az AOB hegyesszög 60 fokos lesz.
A 60 fokos szögből felezéssel kapható a 30 fokos szög. Derékszög nyerhető egy 60 és egy 30 fokos szög egymás mellé másolásával, vagy az egyenesszög megfelezésével.
Ezekkel a szögekkel szerkeszthetők szabályos hatszögek, szabályos háromszögek, téglalapok és négyzetek.
A 90 fokos szög (derékszög) szerkesztése[szerkesztés]
Derékszög szerkesztésekor egy előre megadott, vagy felvett szakasz felezőmerőlegesét szerkesztjük meg.
Merőleges állítása egyenesre annak egy pontjában[szerkesztés]
Nevezzük az egyenest -nek, és az adott pontot -nek!
- Húzunk egy tetszőleges sugarú kört középponttal. A kört két pontban metszi.
- Egyforma sugarú köröket húzunk a metszéspontok körül. A sugarat akkorának kell választani, hogy ezek a körök messék egymást.
- Összekötjük a két kör metszéspontjait. Az így kapott szakasz a egyenest a pontban merőlegesen metszi.
Merőleges állítása egyenesre külső pontból[szerkesztés]
Legyen ismét az egyenes, és az adott pont !
- Húzunk egy kört középponttal és akkora távolsággal, ami nagyobb, mint a pont és az egyenes távolsága. A kört két pontban metszi.
- Egyforma sugarú köröket húzunk a metszéspontok körül. A sugarat akkorának kell választani, hogy ezek a körök messék egymást.
- Összekötjük a két kör metszéspontjait. Az így kapott egyenes merőlegesen metszi a egyenest, és átmegy a ponton.
Merőleges állítása adott metszéspont nélkül[szerkesztés]

Legyen az egyenes továbbra is !
- A egyenesen tetszőlegesen felvesszük a különböző és pontokat.
- Húzunk két kört egyforma sugárral és körül, hogy messék egymást. A két metszéspontot összekötve merőlegest kapunk a egyenesre.
Diszkusszió[szerkesztés]
Nem kell a teljes köröket felrajzolni. Elég csak akkora köríveket behúzni, hogy a metszéspontok megtalálhatók legyenek.
Minél messzebb vesszük fel a segédpontokat, annál pontosabb lehet a szerkesztés, hiszen annál kisebb hatása van a behúzott vonalak vastagságának. Viszont ha nagy a távolság, akkor a körök laposabb szögben metszik egymást, ami növeli a pontatlanságot.
Szakaszfelező merőleges[szerkesztés]

Hasonló szerkesztéssel lehet kijelölni szakaszfelező merőlegest: a szakasz végpontjai körül köröket húzunk egyforma sugárral, és összekötjük ezek metszéspontjait.
30 fokos szög szerkesztése[szerkesztés]
Habár 30 fokos szög megkapható a 60 fokos szög felezésével, azért 30 fokos szög egyszerűbben is szerkeszthető.
Adott egyenest adott pontjában 30 fokban metsző egyenes szerkesztése[szerkesztés]

Legyen az egyenes , az adott pont !
- Felveszünk egy tetszőleges pontot az egyenesen, és kört húzunk középponttal a ponton át. Adódik a metszéspont.
- Kört húzunk a pont körül ugyanezzel a sugárral, és legyen a két kör egyik metszéspontja .
- A egyenes -et 30 fokban metszi.
Adott egyenest adott külső ponton átmenő, 30 fokban metsző egyenes szerkesztése[szerkesztés]
Legyen az egyenes , az adott pont !
- Tetszőleges sugárral kört húzunk körül, ami -et az , pontokban metszi.
- Az pont körül sugárral kört húzunk. Hasonlóan, körül ugyanezzel a sugárral kört húzunk. A két kör túloldali metszéspontját jelölje .
- A egyenes metszéspontja -gyel .
- sugárral kört húzunk és körül is. Adódik az pont.
- -t -vel összekötve adódik az pont.
- sugárral kört húzunk körül, a -gyel vett metszéspont .
- sugárral kört rajzolunk a pont körül, ez a egyenest a pontban metszi.
- A egyenes -et 30 fokban metszi.
Egy alternatív szerkesztésmód a 60 fokos szög alternatív szerkesztésén alapul. Az ottani jelölésekkel az ötödik kör középpontú, -n átmenő kör, a 30 fokban metsző egyenes a egyenes.

A szabályos ötszögből kapható szögek[szerkesztés]
Szabályos ötszög szerkeszthető, így a 72, a 108 és az 54 fokos szögek. Ezekkel tovább bővül a szerkeszthető szögek köre.
Szabályos ötszög szerkeszthető például adott a oldalhosszból:
- Felvesszük az adott oldalhosszt A és B végpontokkal, "a" szakaszhossz.
- Megszerkesztjük AB felezőmerőlegesét
- Felmérjük a felezőmerőlegesre az "a" szakaszhosszt; az így kimetszett pont Q
- Az AQ szakasz meghosszabbítására felmérjük az "a" hossz felét; az így kimetszett pont R. Az AR szakasz hossza adja az ötszög átlójának hosszát, d-t
- Az AB felezőmerőlegesből az A-ból húzott d sugarú körív kimetszi D-t. Ezzel megkaptuk a szabályos ötszög egy oldala és egy átlója által bezárt szöget
- Az ötszög hiányzó két csúcsa a már meglevő csúcsokból húzott a sugarú körívekkel.
Ezzel megkapjuk a szabályos ötszög belső szögeként a 108 fokos szöget, ennek kiegészítő szögeként a 72 fokos szöget, és felezéssel az 54 fokos szöget.

Általános szögszerkesztések[szerkesztés]

A 9° és a 3° szerkesztéséhez szükség van a 30° és a szabályos ötszög szerkesztésére
Szerkeszthetők a fenti szögek, 90°, 60°, 72° illetve 54°; ezek összegei, különbségei, és felezéssel (ami tetszőleges számszor megismételhető) további szögek kaphatók. Például 3° kapható a következőképpen: . Általában szerkeszthetők azok a szögek, melyek szinusza (koszinusza) előáll egész számokból alapműveletekkel és négyzetgyökvonásokkal. Ez teljesül például minden olyan szögre, ami a 3°-os szög egész számú többszöröse: [3]
A szögfelezés kifejezhető a felezési tételekkel:
- és
Az összeadások, kivonások követhetők az addíciós tételekkel:
- und
Kiszámítható, hogy a 17-szög középponti szögének koszinusza:
- ,
ami szerkeszthetőségét igazolja.
Tételek a szögekről[szerkesztés]
- Összefüggések a háromszög oldalai és szögei között: a háromszögben a legnagyobb oldallal szemben van a legnagyobb szög
- Kerületi és középponti szögek tétele: a középponti szög a hozzá tartozó kerületi szög kétszerese
- Speciális eset: Thalész-tétel: egy kör átmérőjéből a kör pontjai derékszögben látszanak
- Pitagorasz-tétel a derékszögű háromszögekről: a két befogó négyzetösszege az átfogó négyzete
- Befogótétel és magasságtétel

Trigonometria[szerkesztés]
A trigonometrikus függvények vagy szögfüggvények eredetileg egy derékszögű háromszög egy szöge és két oldalának hányadosa közötti összefüggést írják le.
A szögfüggvényeknek a derékszögű háromszög két oldalának hányadosa és a szög összefüggésén kívül az egységsugarú körben tekintett forgásszög-végpontok metszeteivel (vetületeivel, koordinátáival) is definiálhatók. Ez utóbbi definíció már 90°, azaz π/2-nél nagyobb, sőt negatív (mindent összevéve, tetszőleges valós) argumentumokra is működik.
A szögfüggvények segítségével pontosíthatók az összefüggések a háromszögek oldalai és szögei között:
- Szinusztétel: egy háromszög oldalainak aránya megegyezik a szemközti szögek szinuszainak arányával. A háromszög oldalai és szögei közötti összefüggés pontos alakja
- Koszinusztétel: : A Pitagorasz-tétel általánosítása
Kapcsolódó szócikkek[szerkesztés]
Jegyzetek[szerkesztés]
- ↑ W3spoint.com: Angle between two lines Archiválva 2021. június 24-i dátummal a Wayback Machine-ben
- ↑ emathzone.com: Angle of Intersection of Two Lines
- ↑ Liste
Források[szerkesztés]
- Matematikai kisenciklopédia, Gondolat Kiadó, Budapest, 1968
- Bokor József (szerk.). Belső szög, A Pallas nagy lexikona. Arcanum: FolioNET (1893–1897, 1998.). ISBN 963 85923 2 X
- Szögek értelmezése térben
- Síkszög, lapszög, térszög
- Nevezetes szögpárok
- Szögfelezés; 60, 30 és 90 fokos szögek szerkesztése
- Szabályos ötszög szerkesztése adott oldalhosszból Archiválva 2009. december 29-i dátummal a Wayback Machine-ben
- Összefüggések a háromszög oldalai és szögei között[halott link]
- Középponti és kerületi szögek tétele Archiválva 2010. április 19-i dátummal a Wayback Machine-ben
- Thalész-tétel Archiválva 2011. február 28-i dátummal a Wayback Machine-ben
- Befogó- és magasságtétel
- Szinusztétel
- Koszinusztétel
- José Matos: [The Historical Development of the Concept of Angle] (A szög fogalmának történeti fejlődése ). (PDF, angol nyelv). The Mathematics Educator Online, 1. évf. 1. sz. Beill. 2010. szeptember 19.
Fordítás[szerkesztés]
Ez a szócikk részben vagy egészben a Winkel című német Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.









![{\displaystyle [BA]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/28e56d00eabfbd70f8db2b8c78f8f536bce7d87b)
![{\displaystyle [BC]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd2ee765006b05ac0001c01a206871306f108cbc)