Hiperbolikus geometria
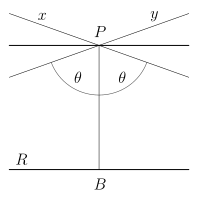


A hiperbolikus geometria egy nemeuklideszi geometria, amiben az euklideszi párhuzamossági axiómát a hiperbolikus axióma helyettesíti. Ez azt mondja ki, hogy egy egyeneshez egy rajta kívül fekvő ponton át több párhuzamos húzható. Ennek több meglepő következménye is van, például két metsző egyeneshez van egy harmadik, ami egyiket sem metszi.
A párhuzamosság terminológiája nem egységes. Ami az egyikben párhuzamos, az a másikban elpattanó, de használják a párhuzamos szót az összes nem metsző egyenesre is. Ezért mindig meg kell ismerni az adott helyen alkalmazott terminológiát. Itt az elpattanó, az ultrapárhuzamos és a párhuzamos szavakat használjuk majd. A párhuzamos az egy síkban levő nem metsző egyeneseket, az elpattanó a határhelyezetben párhuzamos, és az ultrapárhuzamos a nem elpattanó, de párhuzamos egyeneseket jelöli.
A hiperbolikus sík negatív görbülete miatt nem ágyazható be az euklideszi térbe, de modellezhető már az euklideszi síkban is. Több modellje is létezik, mint a Klein-modell, a hiperboloidmodell, és a konform modellek. A modellek azt mutatják, hogy ha az euklideszi axiómarendszer ellentmondásmentes, akkor a hiperbolikus axiómarendszer is az. Az euklideszi geometriát is modellezték a hiperbolikusban, így a két axiómarendszer ellentmondásmentessége ekvivalens.
Története[szerkesztés]

A hiperbolikus geometria felfedezőjeként Bolyai Jánost és Nyikolaj Ivanovics Lobacsevszkijt tartják számon, de már előttük is sok eredmény született róla.
A párhuzamossági axióma már az ókor óta foglalkoztatta a matematikusokat és a filozófusokat, mivel bonyolultabb, mint a többi euklideszi axióma. Aquinói Szent Tamás arról értekezett, hogy Isten nem tud olyan háromszöget teremteni, aminek szögeinek összege nem 180 fok. Sok geométer próbált az egy ponton átmenő több párhuzamos létezéséből ellentmondást kicsikarni, így Proklosz, Ibn al-Haytham, Omar Hajjám,[1] Naszír ad-Dín Túszí, Witelo, Gersonides, Alfonso, később Giovanni Gerolamo Saccheri, John Wallis, Johann Heinrich Lambert, és Legendre.[2] Sokuk az eredmények bizarrsága miatt arra jutott, hogy ez már ellentmondás, pedig valójában nem volt ellentmondás, csak a szemléletük csapta be őket.
Az arab tudósok által tanulmányozott négyszögek tulajdonságai adták az első hiperbolikus geometriai tételeket. Kutatásaik erősen hatottak a későbbi európai geométerekre.[3] Johann Heinrich Lambert a 18. században bevezette a hiperbolikus függvényeket, és kiszámította a hiperbolikus háromszög területét.
Bolyai és Lobacsevszkij egymástól függetlenül mélyedtek el a hiperbolikus geometriában. Lobacsevszkij műve 1830-ban, Bolyai Appendixe 1832-ben jelent meg. A kortársak nem értették meg ezeket az eredményeket, oktalanságnak tartották. Carl Friedrich Gauss is tanulmányozta, de csak leveleiben írt róla, eredményeit nem jelentette meg.
Az első modellt Eugenio Beltrami alkotta meg 1868-ban. Felix Christian Klein 1871-ben nevezte először hiperbolikusnak ezt a geometriát.[4]
Paramétere[szerkesztés]
A hiperbolikus alakzatoknak az euklideszi geometriától eltérő tulajdonságai vannak, de kis, a -val összemérhető távolságokon (K< 0 Gauss-görbület) nehéz felismerni, hogy a geometria nem euklideszi. A különböző Gauss-görbületű hiperbolikus síkok, terek hasonlóak, akár a különböző sugarú gömbök.
Ez a mennyiség a hiperbolikus geometria természetes hosszegysége, amit a hiperbolikus geometria paraméterének is neveznek. Többnyire ebben a mértékegységben mérik a távolságokat, mert így egyszerűbbek lesznek a képletek.
Modelljei[szerkesztés]

A következőkben a hiperbolikus sík modelljeit mutatjuk be, de a magasabb dimenziós hiperbolikus tér is modellezhető. Mindegyik modell ugyanazt a hiperbolikus síkot modellezi, transzformálhatók egymásba. A pszeudoszférával csak a sík egy része modellezhető.
Beltrami-Klein-féle körmodell[szerkesztés]

- Sík: nyílt körlap
- Pontok: a nyílt körlap pontjai
- Egyenesek: a körlap húrjai végpontok nélkül. Ezek a pontok végtelen távoli pontok; halmazuk a hiperbolikus sík határköre.
A modellben a középpontban a hiperbolikus szög megegyezik az euklideszi értelemben mérhető szöggel; máshol ez nem igaz, a modell nem szögtartó. Két egyenes merőleges, ha projektív értelemben konjugáltak. A távolságmérés bonyolultabb, mint az euklideszi távolság mérése.
Jelölje a két pontot A és B! Tekintsük a rajtuk átmenő hiperbolikus egyenes végtelen távoli pontjait; legyenek ezek R és S! Ekkor az AB távolság
- ,
ahol (ABRS) a négy pont komplex értelemben vett kettősviszonya.
Ez a modell kiterjeszthető magasabb dimenzióba is.
Konform körmodell[szerkesztés]
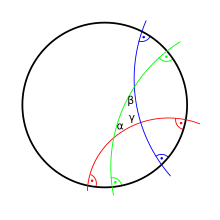
A félgömbmodellből inverzióval a pólus alkalmas megválasztásával kapható.
- Sík: nyílt körlap
- Pontok: a nyílt körlap pontjai
- Egyenesek: az átmérők és a határkört merőlegesen metsző körívek. A többi körív olyan hiperciklus, ami nem egyenes.
Ebben a modellben a szögek mindenütt megegyeznek az euklideszi értelemben mérhető szöggel, vagyis ez egy szögtartó modell. A távolságmérés itt is a kettősviszonyra támaszkodik:
Jelölje a két pontot A és B! Tekintsük a rajtuk átmenő hiperbolikus egyenes végtelen távoli pontjait; legyenek ezek R és S! Ekkor az AB távolság
- ,
ahol (a,b,r,s) köri, vagy hagyományos értelemben vett kettősviszony.
Konform félsíkmodell[szerkesztés]
A konform félsíkmodell a konform körmodell egy változatának tekinthető, amiben a határkör egy egyenes. Abból inverzióval kapható, ahol az inverzió középpontja a határkör egy pontja.
- Sík: nyílt félsík
- Pontok: a nyílt félsík pontjai
- Egyenesek: a határegyenesre merőleges egyenesek és az azt merőlegesen metsző félkörök
Ez a modell is szögtartó. A távolságok ugyanúgy mérhetők, mint a körmodellben, kivéve, ha a két pont egy félegyenesre esik. Ekkor a képletben (b-u)=(b-v)=1.
Félgömbmodell[szerkesztés]
A Beltrami-Klein-féle körmodell félgömbre vetítésével kapható.
- Sík: nyílt félgömb
- Pontok: a nyílt félgömb pontjai
- Egyenesek: a félgömb egyenlítőjét merőlegesen metsző körök. A többi körív valódi hiperciklus.
A szögek megfelelnek az euklideszi értelemben vett szögeknek, és a távolság a konform modelleken megszokott módon mérhető.
Elemei[szerkesztés]
Egyenesek[szerkesztés]

A hiperbolikus axióma szerint egy adott egyeneshez egy rajta nem fekvő ponton át több egyenes is átmegy, ami az adott egyenest nem metszi. Ezek az egyenesek két szögtartományt alkotnak, amiket az elpattanó egyenesek határolnak. A hiperbolikus síkban az egyenesek kölcsönös viszonya többféle lehet, mint az euklideszi geometriában, mivel kétféle párhuzamosság létezik. Helyesebb azonban irányított egyenesek elpattanásáról beszélni, mivel csak az egyik irányba pattannak el egymástól. Ekkor az elpattanó tulajdonság szimmetrikus, reflexív és tranzitív, az ultrapárhuzamosság azonban így sem tranzitív.
Legyen most adva az e irányított egyenes a rajta kívül fekvő P ponttal! Jelölje a P-ből az e-re állított merőleges talppontját Q, a P-n átmenő, az adott irányhoz tartozó e-től elpattanó egyenest ea, és az e és ea által bezárt szöget α! Ha még a PQ párhuzamossági távolság d, akkor α a d távolsághoz tartozó párhuzamossági szög. Belátható, hogy ez a szög csak az egyenes és a rajta kívül fekvő pont távolságától függ, csak hegyesszög lehet, és értéke tetszőlegesen megközelítheti a nullát. Megmutatható, hogy a párhuzamossági távolság és a párhuzamossági szög kapcsolata kölcsönösen egyértelmű. Nagy távolságokra a párhuzamossági szög kicsi.
Néhány jellegzetes tulajdonság:
- Az ultrapárhuzamos egyeneseknek van egy egyértelmű közös egyenesük.
- Minden egyenespárnak van szimmetriatengelye.
- Az egy egyenestől adott távolságra levő pontok hiperciklust alkotnak, és ha a távolság pozitív, akkor ez a hiperciklus nem egyenes.
Háromszögek[szerkesztés]

A hiperbolikus síkban a háromszögek szögeinek összege mindig kisebb, mint 180 fok. Ez ekvivalens a hiperbolikus axiómával. Azt a mennyiséget, amennyivel a háromszög szögösszege kisebb, mint 180 fok, a háromszög (hiperbolikus) defektusának nevezzük: δ=π-(α+β+γ).
A terület nem számítható úgy, mint az euklideszi geometriában, mivel a háromszög oldala és a hozzá tartozó magasság szorzata a három oldalra nézve különböző lehet. Ehelyett a terület a gömbi geometriához hasonlóan számítható, csak nem a gömbi felesleggel, hanem a hiperbolikus defektussal kell számolni. A háromszög területe k2δ. Eszerint a háromszögek területe nem lehet akármilyen nagy.
A hiperbolikus geometriában vannak egyszeresen, kétszeresen és háromszorosan aszimptotikus háromszögek, amiknek egy, két vagy három elpattanó oldaluk van. Mivel az elpattanó egyenesek által bezárt szög az elpattanás irányában nulla, ezért ezekben a háromszögekben nulla fokos szögek is vannak.
A hiperbolikus geometriában két háromszög egybevágó, ha:
- mindhárom oldaluk megegyezik
- két oldaluk, és a közrezárt szögük megegyezik
- két oldaluk, és a nagyobbal szemben fekvő szög megegyezik
- egy oldaluk, és a rajta fekvő szögek megegyezik
- mindhárom szögük megegyezik
Az euklideszi geometriában ez az utóbbi eset csak a háromszögek hasonlóságát bizonyítaná, sőt a harmadik szög fölöslegesen lenne megadva. A hiperbolikus geometriában azonban, akárcsak a gömbi geometriában, nincsenek valódi hasonlóságok, így amik hasonlók, azok egybevágók is. Tulajdonképpen a valódi hasonlóságok megváltoztatják a hiperbolikus sík paraméterét, ezzel egy másik hiperbolikus síkra kerülünk át.
A hiperbolikus geometriában is ki lehet számítani a háromszögek három független adatából a többi adatát. Ehhez a hiperbolikus trigonometria nyújt segítséget:
- szinusztétel: .
- I. koszinusztétel: .
- II. koszinusztétel:
Négyszögek[szerkesztés]

A hiperbolikus síkban a négyszögek szögeinek összege kisebb, mint 360 fok, ezért nincsenek téglalapok. Nem használják a négyzet elnevezést sem, mert beleértik a definíciójába, hogy négy derékszöge van, ehelyett szabályos négyszögekről beszélnek.
Bolyai János eredményei szerint a hiperbolikus síkban van négyszögesíthető kör, vagyis amihez szerkeszthető szabályos négyszög, aminek területe megegyezik a kör területével.
Ciklusok[szerkesztés]


A ciklusok a hiperbolikus sík jellegzetes alakzatai. Ha egy pontot végigtükrözünk egy sugársor elemein, akkor a tükörképek a kiindulási ponttal együtt ciklust adnak. Mivel a hiperbolikus geometriában háromféle sugársor létezik: metsző, elpattanó és ultrapárhuzamos, azért ennek megfelelően háromféle ciklus van: ezek rendre a kör, a paraciklus és a hiperciklus. A sugársort két egyenese már meghatározza, ezért egy ciklus egyértelműen megadható három adatával, a sugársor két egyenesével és egy pontjával.
Uniform görbék, azaz önmagukban eltolhatók. Az egyenesek távolságvonala hiperciklus. A paraciklus végtelen sugarú körnek tekinthető. A háromszögeknek mindig van beírt körük, de körülírt körük nem mindig, azonban körülírt ciklusuk mindig van, ami lehet kör, hiperciklus vagy paraciklus. A sík bármely három pontján át van ciklus.
A hiperbolikus geometriában a kör kerülete nagyobb, mint 2rπ. Pontosabban
A körlap területe
A gömb felszíne térfogata .
Az n dimenziós gömbök felszíne térfogata .
Transzformációk[szerkesztés]
Valódi hasonlóságok nincsenek, de az egybevágóság abszolút geometriai fogalom. A hiperbolikus síkon is léteznek tükrözések, forgatások, eltolások. Kétféle eltolás különböztethető meg: a párhuzamos eltolásnak megfelelő egyenes menti eltolás, és a paraciklikus eltolás, ami két egyirányú egyenesre való tükrözéssel áll elő. Az egyenes menti eltolás az adott egyenesre merőleges két egyenesre való tükrözés szorzata. Az így kapott eltolás nem függ a konkrét merőlegesektől, csak a köztük levő távolságtól. Az eltolások irányát a tükrözések sorrendje adja meg. A középpontos tükrözés két merőleges egyenesre való tükrözéssel definiálható.
Míg az euklideszi sík hasonlóság erejéig csak néhány háromszöggel parkettázható, addig a hiperbolikus síkon végtelen sokféle olyan háromszög létezik, amik egybevágó példányai egyrétegűen lefedik a síkot. Az euklideszi sík a szabályos sokszögek közül csak háromszögekkel, négyszögekkel és hatszögekkel parkettázható; a hiperbolikus sík viszont bármely olyan n-szöggel parkettázható, amire , ahol a sokszög egy szöge a teljesszög l-edrésze, vagy 0 fok.
A hiperbolikus sík transzformációi a félsíkmodellben éppen a félsíkot önmagába átvivő Möbius-transzformációk.
Koordináta-rendszer[szerkesztés]
Az euklideszi Descartes-koordináta-rendszernek több ekvivalens definíciója van. Az egyik mindkét tengelyen kijelöli a megfelelő koordinátákat, ezekből merőlegeseket állít, majd ezek metszéspontját tekinti az adott koordinátájú pontnak. A másik definíció először az x tengelyen megy az első koordinátának megfelelő számú lépést, majd arra merőlegesen lépi le az y koordinátának megfelelő lépést.
Mivel a hiperbolikus síkon nincs téglalap, itt a két definíció már nem lesz ekvivalens, hanem különböző koordináta-rendszerekhez vezet. Az origó k nagyságrendű környezetében ez ugyan csak kisebb pontatlanságokat jelent, de bizonyos koordináta-párok hiányozni fognak az első definíció szerinti koordináta-rendszerből, mivel a megfelelő egyenesek ultrapárhuzamosok lesznek. Ez nagy számokra lesz így. A második definíció által adott rendszerben azok a pontok, amiknek a második koordinátája megegyezik, hiperciklust adnak. A távolsággal olyan koordináta-rendszer is megadható, ahol a koordinátavonalak hiperciklusok, és ha különböznek a tengelytől, akkor nem egyenesek.
Alkalmazása[szerkesztés]
Alkalmazzák a görbült terek elméletében és a fizikában, mint a tér lehetséges alakját. Már maga Bolyai János is elgondolkodott azon, hogy vajon melyik geometria írja le jobban a fizikai teret. Ha a k paraméter elég nagy, akkor a mérési pontatlanságok miatt nem lehet eldönteni, hogy melyik geometria valósul meg; ezért akár egy megfelelően paraméterezett hiperbolikus geometria is megfelel.
A művészetekben[szerkesztés]
Maurits Cornelis Escher holland grafikus előszeretettel ábrázolta a hiperbolikus sík különféle csempézéseit. A Körhatár III. és a Körhatár IV. metszetein a konform körmodell látható. A fehér vonalak a képeken az egyenesekhez közeli hiperciklusok. Látni lehet a negatív görbület hatását a sokszögek szögeinek összegére. Például a Körhatár III.-ban egy-egy csúcsban három-három háromszög és négyszög találkozik; ez az euklideszi síkban lehetetlen lenne. A modell másik jellegzetessége, hogy a széle felé haladva a minta összesűrűsödni látszik, miközben a hiperbolikus terület azonos marad. Ezek a képek nem lettek népszerűek a művészek körében, de a matematikusoknak tetszettek.
William Thurston papírból készített pszeudoszférát. A marosvásárhelyi Bolyai-emlékmű harsonája is pszeudoszféra alakú. Daina Taimina horgolt terítőkkel modellezte a hiperbolikus síkot.[5] Könyve a Crocheting Adventures with Hyperbolic Planes címmel jelent meg, és elnyerte a Bookseller Legfurcsább Cím Díját 2009-ben.[6] Keith Henderson papírból elkészítette a hiperbolikus sík egy csempézésének gyorsan összeállítható modelljét. Jeff Weeks leírta, hogyan lehet a Helaman Ferguson által tervezett hiperbolikus ágytakarókat elkészíteni.[7][8]
Jegyzetek[szerkesztés]
- ↑ Omar Khayyam 1048-1131. [2007. szeptember 28-i dátummal az eredetiből archiválva]. (Hozzáférés: 2008. január 5.)
- ↑ http://www.math.columbia.edu/~pinkham/teaching/seminars/NonEuclidean.html
- ↑ Boris A. Rosenfeld and Adolf P. Youschkevitch (1996), "Geometry", in Roshdi Rashed, ed., Encyclopedia of the History of Arabic Science, Vol. 2, p. 447-494 [470], Routledge, London and New York
- ↑ F. Klein, Über die sogenannte Nicht-Euklidische, Geometrie, Math. Ann. 4, 573-625 (cf. Ges. Math. Abh. 1, 244-350).
- ↑ Hyperbolic Space. The Institute for Figuring, 2006. december 21. (Hozzáférés: 2007. január 15.)
- ↑ Bloxham, Andy (2010. március 26.). „Crocheting Adventures with Hyperbolic Planes wins oddest book title award”. The Telegraph. .
- ↑ Helaman Ferguson, Hyperbolic Quilt. [2011. július 11-i dátummal az eredetiből archiválva]. (Hozzáférés: 2010. október 25.)
- ↑ How to sew a Hyperbolic Blanket
Források[szerkesztés]
- Kertész‑Nagy:A hiperbolikus geometria összefoglalása[halott link]
- NonEuclid
- Szilassi Lajos előadásai
- Surányi az euklideszi és a hiperbolikus geometriáról
- KöMaL: Hiperbolikus Escher-grafikák
- Bolyai János: Appendix Magyarázat az Appendixhez
- Reiman István: Geometria és határterületei
- D. Richtmyer, Introduction to hyperbolic geometry, Springer 1995, pp. 215-217.













