Prímhézag

A matematika, azon belül a számelmélet területén a prímhézag (prime gap, jelölése a gap-ből gyakran g) két egymást követő prímszám közötti különbséget jelenti. Az n-edik prímhézag, jelölje g_n vagy g(p_n) az (n + 1)-edik és az n-edik prímszámok közötti különbség:

$g_{n}=p_{n+1}-p_{n}.\$

Így tehát g₁ = 1, g₂ = g₃ = 2, g₄ = 4 stb. A prímhézagok (g_n) sorozatát átfogóan tanulmányozták, mégis számos nyitott kérdés és sejtés létezik velük kapcsolatban.

Az első 60 prímhézag:

1, 2, 2, 4, 2, 4, 2, 4, 6, 2, 6, 4, 2, 4, 6, 6, 2, 6, 4, 2, 6, 4, 6, 8, 4, 2, 4, 2, 4, 14, 4, 6, 2, 10, 2, 6, 6, 4, 6, 6, 2, 10, 2, 4, 2, 12, 12, 4, 2, 4, 6, 2, 10, 6, 6, 6, 2, 6, 4, 2, ... (A001223 sorozat az OEIS-ben).

A g_n sorozat definíciójából következik, hogy minden prímszám felírható a következő alakban:

$p_{n+1}=2+\sum _{i=1}^{n}g_{i}.$

Egyszerű megfigyelések

Az első, legkisebb, és egyetlen páratlan prímhézag (1) az egyetlen páros prímszám (2) és az első páratlan prímszám (3) között van. Az összes többi prímhézag páros. Egyetlen olyan prímhézag-páros van, ami maga is prímszámokból áll, a g₂ és g₃ a 3, 5 és 7 között.

Bármely P prímszám esetén P#-tel jelöljük P primoriálisát, tehát az összes prímszám szorzatát P-ig bezárólag, P-t is beleértve. Ha Q a P-t közvetlenül követő prímszám, akkor a következő sorozat:

$P\#+2,P\#+3,\ldots ,P\#+(Q-1)$

Q − 2 egymást követő egész számot tartalmaz, tehát itt a prímhézag legalább Q − 1 hosszúságú. Ebből következik, hogy tetszőlegesen nagy prímhézagok léteznek, így tehát bármely P prímszámhoz tartozik olyan n egész szám, ahol g_n ≥ P. (Belátható, ha n-et úgy választjuk meg, hogy p_n a legnagyobb prímszám, ami kisebb P# + 2-nél.) A tetszőlegesen nagy prímhézagok létezése a prímszámtételből kiindulva is belátható, mi szerint a prímszámok sűrűsége közelít a nullához. A tétel szerint P# igen durva közelítésben exp(P) nagyságú, exp(P) környezetében pedig az egymást követő prímszámok közötti átlagos távolság P.

A gyakorlatban a P méretű prímrések a P#-nál jóval előbb jelentkeznek. Például a 71 egymást követő összetett számból álló szekvencia először 31398 és 31468 között jelentkezik, míg a 71# huszonhét számjegyből áll – tízes számrendszerben 557940830126698960967415390.

Bár a prímszámok közti átlagos hézag nagysága a számok természetes logaritmusa szerint növekszik, a maximális prímhézag és a benne foglalt egészek közötti arány szintén nő, ahogy egyre nagyobb számok és prímhézagok fordulnak elő.

Az ellenkező irányt tekintve, az ikerprímsejtés szerint g_n = 2 végtelen sok n helyen.

Numerikus eredmények

2017 márciusában az ismert legnagyobb prímhézag azonosítható valószínű prím végekkel 5 103 138 hosszúságú, a hozzá tartozó 216849 jegyű valószínű prímeket Robert W. Smith találta, ennek a jósága M=10,2203. A legnagyobb ismert prímhézag, aminek a szélein bizonyítottan prímszámok találhatók, 1 113 106 hosszúságú, a szélein lévő 18662 jegyű prímszámokat P. Cami, M. Jansen és J. K. Andersen találták meg.

Nevezzük g_n-t maximális prímhézagnak, ha g_m < g_n minden m < n esetben. 2016 júniusában a legnagyobb ismert maximális prímhézag 1476 hosszúságú, Tomás Oliveira e Silva találta meg. Ez sorrendben a 75. maximális hézag, és az 1425172824437699411 prímszám után következik. További maximális prímhézag-rekordok találhatók itt:  A002386.

Egy prímhézag jóságán (merit) a g_n / ln(p_n) arány értendő. 1931-ben E. Westzynthius bebizonyította, hogy a prímhézagok logaritmikusnál gyorsabban nőnek. Tehát,

$\limsup _{n\to \infty }{\frac {g_{n}}{\log p_{n}}}=\infty .$

Legnagyobb ismert jóság-értékek (2016-11)

Jóság	gn	számjegyek	pn	Dátum	Felfedező
36,858288	10716	127	7910896513·283#/30 − 6480	2016	Dana Jacobsen
36,590183	13692	163	1037600971·383#/210 − 8776	2016	Dana Jacobsen
36,420568	26892	321	59740589·757#/210 − 14302	2016	Dana Jacobsen
35,424459	66520	816	1931·1933#/7230 − 30244	2012	Michiel Jansen
35,310308	1476	19	1425172824437699411	2009	Tomás Oliveira e Silva
34,975687	1442	18	804212830686677669	2005	Siegfried Herzog

2016. novemberi adat szerint a legnagyobb ismert jósági érték 10716 / ln(7910896513·283#/30 − 6480) ≈ 36,858288 (283# 283 primoriálisát jelöli). A végpontok 127 jegyű prímek.

A Cramér–Shanks–Granville-arány a következő szám:

${\frac {g_{n}}{\log ^{2}p_{n}}}$

Az arány legnagyobb ismert értéke 0,9206386, ami az 1693182318746371 prímszámhoz tartozik. Megoszlanak a vélemények, hogy az arány eléri-e az egyet; további rekordértékek itt találhatók:  A111943.

Az első 75 maximális prímhézag (n értéke nem szerepel)

1 – 25 # gn pn 1 1 2 2 2 3 3 4 7 4 6 23 5 8 89 6 14 113 7 18 523 8 20 887 9 22 1129 10 34 1327 11 36 9551 12 44 15 683 13 52 19 609 14 72 31 397 15 86 155 921 16 96 360 653 17 112 370 261 18 114 492 113 19 118 1 349 533 20 132 1 357 201 21 148 2 010 733 22 154 4 652 353 23 180 17 051 707 24 210 20 831 323 25 220 47 326 693

26 – 50 # gn pn 26 222 122 164 747 27 234 189 695 659 28 248 191 912 783 29 250 387 096 133 30 282 436 273 009 31 288 1 294 268 491 32 292 1 453 168 141 33 320 2 300 942 549 34 336 3 842 610 773 35 354 4 302 407 359 36 382 10 726 904 659 37 384 20 678 048 297 38 394 22 367 084 959 39 456 25 056 082 087 40 464 42 652 618 343 41 468 127 976 334 671 42 474 182 226 896 239 43 486 241 160 624 143 44 490 297 501 075 799 45 500 303 371 455 241 46 514 304 599 508 537 47 516 416 608 695 821 48 532 461 690 510 011 49 534 614 487 453 523 50 540 738 832 927 927

51 – 75 # gn pn 51 582 1 346 294 310 749 52 588 1 408 695 493 609 53 602 1 968 188 556 461 54 652 2 614 941 710 599 55 674 7 177 162 611 713 56 716 13 829 048 559 701 57 766 19 581 334 192 423 58 778 42 842 283 925 351 59 804 90 874 329 411 493 60 806 171 231 342 420 521 61 906 218 209 405 436 543 62 916 1 189 459 969 825 483 63 924 1 686 994 940 955 803 64 1132 1 693 182 318 746 371 65 1184 43 841 547 845 541 059 66 1198 55 350 776 431 903 243 67 1220 80 873 624 627 234 849 68 1224 203 986 478 517 455 989 69 1248 218 034 721 194 214 273 70 1272 305 405 826 521 087 869 71 1328 352 521 223 451 364 323 72 1356 401 429 925 999 153 707 73 1370 418 032 645 936 712 127 74 1442 804 212 830 686 677 669 75 1476 1 425 172 824 437 699 411

További eredmények

Felső korlátok

Az 1852-ben bizonyított Bertrand-posztulátum kimondja, hogy k és 2k között mindig létezik prímszám, így tehát p_n+1 < 2p_n, amiből következik, hogy g_n < p_n.

Az 1896-ban bizonyított prímszámtétel szerint egy p prímszám és a rákövetkező prímszám közötti hézag átlagos nagysága ln(p). Egy konkrét hézag tényleges mérete persze ennél jóval nagyobb vagy kisebb is lehet. A prímszámtételből azonban következik egy felső korlát is: minden ε > 0-hoz létezik N szám, amire g_n < εp_n minden n > N esetben.

Kikövetkeztethető, hogy a prímhézagok a prímek nagyságához képest egyre kisebbek lesznek, tetszőlegesen kicsik: a hányados nullához tart:

$\lim _{n\to \infty }{\frac {g_{n}}{p_{n}}}=0.$

Hoheisel (1930) mutatta meg elsőként, hogy létezik egy θ < 1 konstans, amire

$\pi (x+x^{\theta })-\pi (x)\sim {\frac {x^{\theta }}{\log(x)}}{\text{ ahogy }}x\to \infty ,$

így tehát:

$g_{n}<p_{n}^{\theta },\,$

elegendően nagy n-ekre.

Hoheisel a θ értékét 32999/33000-ra tette. Ezt Heilbronn 249/250-re javította, majd Chudakov θ = 3/4 + ε-re, bármilyen ε > 0-ra.

Ingham nevéhez fűződik egy nagyobb előrelépés, aki megmutatta, hogy ha

$\zeta (1/2+it)=O(t^{c})\,$

valamely pozitív c konstansra, ahol az O az O jelölésre utal, akkor

$\pi (x+x^{\theta })-\pi (x)\sim {\frac {x^{\theta }}{\log(x)}}$

bármely θ > (1 + 4c)/(2 + 4c)-re. Itt a szokásos módon ζ a Riemann-féle zéta-függvény, π pedig a prímszámláló függvény. Tudva, hogy bármely c > 1/6 elfogadható, megállapítható, hogy θ bármely ⅝-nál nagyobb szám lehet.

Ingham eredményének közvetlen következménye, hogy n³ és (n + 1)³ között mindig van prímszám, ha n elegendően nagy. A Lindelöf-sejtés implikálná, hogy Ingham képlete bármilyen pozitív c számra igaz, de még ez sem lenne elég annak igazolására, hogy elegendően nagy n-re mindig van prímszám n² és (n + 1)² között (lásd Legendre-sejtés). Ennek igazolására erősebb eredményre, például a Cramér-sejtésre volna szükség.

Huxley 1972-ben megmutatta, hogy θ választható például θ = 7/12 = 0,58(3)-ra is.

Baker, Harman és Pintz 2001-es eredménye szerint θ levihető akár 0,525-ig.

2005-ben Daniel Goldston, Pintz János és Cem Yıldırım bebizonyították, hogy

$\liminf _{n\to \infty }{\frac {g_{n}}{\log p_{n}}}=0$,

majd két évvel később a következőre javították az eredményt:

$\liminf _{n\to \infty }{\frac {g_{n}}{{\sqrt {\log p_{n}}}(\log \log p_{n})^{2}}}<\infty .$

2013-ban Yitang Zhang igazolta, hogy

$\liminf _{n\to \infty }g_{n}<7\cdot 10^{7},$

ami azt jelenti, hogy végtelen sok 70 milliónál nem nagyobb prímhézag létezik. A Polymath Project keretében végzett együttműködés keretében sikerült Zhang korlátját optimalizálni, 2013. július 20-ára egészen 4680-ig vitték le. 2013 novemberében, James Maynard bemutatta a GPY-szita egy új finomítását, amivel a korlátot 600-ig vitte le, továbbá megmutatta, hogy bármely m-re létezik m prímszámot tartalmazó korlátos intervallum:

$\liminf _{n}(p_{n+m}-p_{n})\ll m^{3}e^{4m}.$

Maynard gondolatait továbbfejlesztve a Polymath project azóta feljavította a korlátot 246-ra. Továbbá, feltételezve az Elliott–Halberstam-sejtés és annak általánosított formájának igazságát, a Polymath project wiki állítása szerint N-et 12-re, illetve 6-ra sikerült lecsökkenteni.

Alsó korlátok

1938-ban Robert Rankin bebizonyította, hogy létezik olyan c > 0 konstans, amire a

$g_{n}>{\frac {c\log n\log \log n\log \log \log \log n}{(\log \log \log n)^{2}}}$

egyenlőtlenség végtelen sok n értékre igaz lesz, továbbfejlesztve ezzel Erik Westzynthius és Erdős Pál eredményeit. Később megmutatta, hogy bármely c < e^γ konstans jó lehet, ahol γ az Euler–Mascheroni-állandó. A c konstans értékét 1997-ben javították bármely 2e^γ-nál kisebb értékre.

Erdős Pál 10 000 dollárt ajánlott annak bizonyításáért vagy cáfolatáért, hogy a fenti egyenlőtlenség c konstansát bármilyen nagyra lehet választani. Ezt 2014-ben sikerült igazolni a Ford–Green–Konyagin–Tao szerzőknek, és tőlük függetlenül James Maynardnak.

Az eredményt Ford–Green–Konyagin–Maynard–Tao tovább javította a következőre:

$g_{n}\gg {\frac {\log n\log \log n\log \log \log \log n}{\log \log \log n}}$

n végtelen sok értékére.

Prímhézagok láncolatára szintén sikerült alsó korlátokat megállapítani.

Prímhézagokkal kapcsolatos sejtések

Prímhézagfüggvény

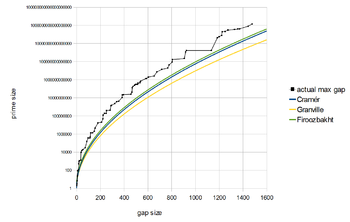
Még jobb eredmények érhetők el, ha a Riemann-sejtést igaznak feltételezzük. Harald Cramér igazolta, hogy a Riemann-sejtésből következik, hogy a g_n prímhézagra teljesül, hogy

$g_{n}=O({\sqrt {p_{n}}}\log p_{n}),$

a nagy O jelölést használva. Későbbi feltételezése szerint a prímhézagok még kisebbek. A Cramér-sejtés durván azt fogalmazza meg, hogy

$g_{n}=O\left((\log p_{n})^{2}\right).$

A Firoozbakht-sejtés kimondja, hogy $p_{n}^{1/n}$ (ahol $p_{n}$ az n-edik prím) n szerint szigorúan csökkenő függvény, tehát

$p_{n+1}^{1/(n+1)}<p_{n}^{1/n}{\text{ minden }}n\geq 1.$

Ha ez a sejtés igaz, akkor a $g_{n}=p_{n+1}-p_{n}$ függvény teljesíti a $g_{n}<(\log p_{n})^{2}-\log p_{n}{\text{ minden }}n>4.$ Következne belőle a Cramér-sejtés egy erős formája, de inkonzisztens lenne a Granville és Pintz által megfigyelt heurisztikákkal, melyek szerint $g_{n}>{\frac {2-\varepsilon }{e^{\gamma }}}(\log p_{n})^{2}$ végtelen sokszor bármely $\varepsilon >0,$-ra, ahol $\gamma$ az Euler–Mascheroni-állandót jelöli.

Oppermann sejtése gyengébb, mint a Cramér-sejtés. Az Oppermann-sejtéssel becsült prímhézag mérete nagyságrendileg:

$g_{n}<{\sqrt {p_{n}}}.$

Ha ez igaz, akkor létezik egy m>0 (valószínűleg m=30) természetes szám, amire minden n>m-re teljesül, hogy $g_{n}<{\sqrt {p_{n}}}.$

Az Andrica-sejtés, ami Oppermann sejtésének gyengébb változata, kimondja, hogy

$g_{n}<2{\sqrt {p_{n}}}+1.$

Ez enyhén erősebb a Legendre-sejtésnél, ami szerint az egymást követő négyzetszámok között mindig található prímszám.

Számelméleti függvényként

Az n-edik és (n + 1)-edik prímszámok közötti g_n prímhézag a számelméleti függvények egy példája. Ebben a kontextusban szokásosan d_n-nel jelölik (magyar kontextusban ez a jelölés általában az osztószám-függvényt illeti), neve pedig prímkülönbség-függvény (prime difference function). A függvény se nem multiplikatív, se nem additív.

Kapcsolódó szócikkek

• Bonse-egyenlőtlenség
• Ikerprím

Fordítás

• Ez a szócikk részben vagy egészben a Prime gap című angol Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.

Jegyzetek

• Guy, Richard K.. Unsolved problems in number theory, 3rd, Springer-Verlag (2004). ISBN 978-0-387-20860-2 

Irodalom

• Soundararajan, Kannan (2007). „Small gaps between prime numbers: the work of Goldston-Pintz-Yıldırım”. Bull. Am. Math. Soc., New Ser. 44, 1–18. o. DOI:10.1090/s0273-0979-06-01142-6. 
• Mihăilescu, Preda (2014. június 1.). „On some conjectures in additive number theory”. Newsletter of the European Mathematical Society, 13–16. o. DOI:10.4171/NEWS. ISSN 1027-488X. 

További információk

• Thomas R. Nicely, Some Results of Computational Research in Prime Numbers -- Computational Number Theory. This reference web site includes a list of all first known occurrence prime gaps.
• Weisstein, Eric W.: Prime Difference Function (angol nyelven). Wolfram MathWorld
• Prime Difference Function a PlanetMath oldalain
• Armin Shams, Re-extending Chebyshev's theorem about Bertrand's conjecture, does not involve an 'arbitrarily big' constant as some other reported results.
• Chris Caldwell, Gaps Between Primes; an elementary introduction
• www.primegaps.com A study of the gaps between consecutive prime numbers
• Andrew Granville, Primes in Intervals of Bounded Length; overview of the results obtained so far up to and including James Maynard's work of November 2013.