Természetes logaritmus
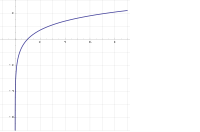
A természetes logaritmus az e alapú logaritmus, ahol e egy irracionális szám, melynek értéke tíz tizedesre: 2,7182818284…
Az e szokásos elnevezése Euler-féle szám, mivel Leonhard Euler svájci matematikus használta először ezt a jelölést 1727-ben.
A természetes logaritmus jelölése ln(x), loge(x) vagy log(x), ha egyértelmű, hogy természetes logaritmusról van szó.[1]
Egy x pozitív szám természetes logaritmusán azt a hatványkitevőt értjük, melyre e-t emelve x-et kapjuk.
Például ln(7,389...) = 2, mert e2=7,389....
Az e természetes logaritmusa 1 (ln(e) = 1), mert e1 = e, továbbá az 1 természetes logaritmusa nulla (ln(1) = 0), mivel e0 = 1.
Bármely a pozitív valós szám természetes logaritmusa definiálható az f(x)=1/x (x>0) függvény görbe alatti területeként (integráljaként) az [1,a] intervallumon. Ennek a definíciónak egyszerűsége vezet a “természetes” jelzőhöz.
A definíció kiterjeszthető nem-zéró komplex számokra is.
A természetes logaritmus függvény, ha valós változók valós függvényeként tekintjük, akkor az exponenciális függvény inverz függvénye:
Mint minden logaritmus, a természetes logaritmus is szorzást összeadásra vezeti vissza:
Az algebrában ennek a tulajdonság a neve izomorfia, amikor egy csoportnál a szorzást összeadásra, az osztást kivonásra lehet átalakítani. Ez a tulajdonság tette lehetővé a logaritmusok használatát a logarléccel történő szorzás, osztás, hatványozás műveleteknél. Manapság nem használnak már logarlécet, de a számológépek belső programjában szintén használható ez az elv.
A logaritmusok bármely 1-nél nagyobb pozitív számra értelmezhetők, nemcsak az e-re. A különféle logaritmus-alapok egy konstans szorzóval különböznek egymástól.
A logaritmusok hasznosak olyan egyenletek megoldásánál, ahol az ismeretlen a kitevőben van. A logaritmusokat például a felezési idő, a bomlási állandó vagy az ismeretlen idő kiszámítására használják exponenciális bomlás esetén.
Történet[szerkesztés]
1668-ban, Nicholas Mercator említette „Logarithmotechnia” című művében a természetes logaritmust.[2] John Speidell, matematikatanár, 1619-ben összeállított egy táblázatot, ahol a természetes logaritmus szerepelt.[3] Gregoire de Saint-Vincent és Alphonse Antonio de Sarasa már 1649 előtt foglalkozott vele.[4] Írásuk a xy = 1 hiperbola kvadratúráját is tartalmazta. Hiperbolikus logaritmusnak is hívták ,[5] mivel a hiperbola görbe alatti területének felel meg. Gregoire de Saint-Vincent és Alphonse Antonio de Sarasa megmutatta azt is, hogy a kvadratúrával definiált logaritmus tulajdonságai a természetes logaritmusra teljesülnek. Szokták néha a Napier-féle logaritmust is természetes logaritmusnak is hívni, de az kissé más jellegű kifejezés.
Jelölési konvenciók[szerkesztés]
Számos változat van forgalomban a természetes logaritmus jelölésére.
Ilyenek: "log(x)" , "ln(x)" vagy loge(x), azaz x természetes logaritmusa, ha pedig 10-es alapú logaritmusról van szó, akkor: "log10(x)".
Az általánosan használt programozási nyelveknél, mint például C, C++, SAS, MATLAB, Fortran, Pascal és BASIC nyelveknél, a "log", "Log" vagy a "LOG" utal a természetes logaritmusra. A zsebszámológépeknél a természetes logaritmust az ln jelöli, a log jelölés a 10-es alapú logaritmus jelölése. Az elméleti számítástechnika tudományban, az információelméletben és a kriptográfiában a "log(x)" általában log2(x)-et jelent (de ezt is szokták lg(x)–nek jelölni).
Természetes logaritmus eredete[szerkesztés]
Kezdetben úgy tűnt, hogy a 10-es alapú logaritmus „természetesebb”, mint az e alapú. Azonban matematikailag a 10 nem különösen szignifikáns. Ennek kulturális okai vannak, meg az, hogy az embernek 10 ujja van.[6] Korábban több kultúra 5, 8, 12, 20 vagy 60 alapú számrendszert használt.[7][8][9]
A természetes logaritmus kitüntetett a hiperbolával való kapcsolata miatt, és azért, mert az 1 helyen a deriváltja (meredeksége) 1. Az e-nél nagyobb alapú logaritmusok esetén ez az érték 1-nél kisebb, kisebb alapok esetén ez az érték 1-nél nagyobb. Ennek a helynek a közelében viszonylag pontosan közelíthető a természetes logaritmus, ha kivonunk a számból 1-et. Így például 1,01 természetes logaritmusa 0,01, 5 tizedesjegy pontossággal. Mindezek a tulajdonságok számrendszertől függetlenek.
A természetes logaritmusra egy példa.
Tekintsük a logaritmusfüggvény differenciálását:[10]
Ha b egyenlő e, akkor a derivált egyszerűen 1/x, és x = 1-nél a derivált 1. Egy másik indok, hogy az e alapú logaritmus a legtermészetesebb, az, hogy könnyen definiálható egyszerű integrálként vagy Taylor-sorként, és ez nem igaz más logaritmusokra. További adalék, hogy több egyszerű sorozat természetes logaritmust használ. Pietro Mengoli és Nicholas Mercator nevezte el természetes logaritmusnak néhány évtizeddel azelőtt, hogy Isaac Newton és Gottfried Wilhelm Leibniz kifejlesztette a matematikai analízist.[11]
Definíciók[szerkesztés]

Az ln(a) definiálható, mint egy integrál, az 1/x függvény integráljaként:
Ez a függvény egy logaritmus, mert kielégíti a logaritmus alapvető tulajdonságát:
Ez jól látható, ha szétválasztjuk az integrált, mely az ln(ab) függvényt két részre bontja, majd behelyettesítést végzünk: x = ta:
Az e szám definiálható, mint egy a valós szám, ahol ln(a) = 1.
Másrészt, ha az exponenciális függvényt definiáljuk először, mondjuk egy végtelen sorral, a természetes logaritmus egy inverz függvényként definiálható, azaz: . Mivel az exponenciális függvény a valós argumentumokra mindig pozitív valós szám, és az exponenciális függvény szigorúan növekvő, ezért ez jól meghatározott minden pozitív x-re.
Tulajdonságok[szerkesztés]
- (a komplex természetes logaritmus egyik értéke)
Deriváltak, Taylor-sor[szerkesztés]

Az ln(1 + x)-re a Taylor-sor csak −1 < x ≤ 1 tartományban ad pontos közelítést. x > 1 esetben a Taylor-sor már nem kielégítő közelítés. A természetes logaritmus deriváltja:
Ez vezet az Taylor-sorához 0 környékén; Mercator-sornak is ismert
és ha x nem egyenlő -1.
A fenti jobb oldali ábrán az ln(1 + x) görbéje látható Taylor-sorral kifejezve 0 körül. Ez a megközelítés csak a −1 < x ≤ 1 tartományban ad pontos közelítést. Ezen tartományon kívül a magasabb rendű Taylor-sorok nem adnak jó megközelítést.
Ha x-t behelyettesítjük x − 1–gyel, akkor ln(x) egy alternatív alakját kapjuk:
Az Euler transzformációt alkalmazva a Mercator-sorra, a következő egyenletet kapjuk, mely minden x-re érvényes, ahol x abszolút értéke nagyobb mint 1:
Ez a sor hasonló a Bailey–Borwein–Plouffe formulához.
Megjegyezhető, hogy egyenlő az inverzével, így egy adott y szám természetes logaritmusa, egyszerűen x-re.
Euler a Taylor-sorba a -1-et behelyettesítve megmutatta, hogy a harmonikus sor határértéke 1/(1-1) természetes logaritmusa, azaz végtelen logaritmusával. Formálisan, de kevésbé szemléletesen belátható, hogy ha N elég nagy, akkor N-ig összegezve a sort az összeg közel lesz ln(N)-hez.
Integrálás természetes logaritmussal[szerkesztés]
A természetes logaritmus egyszerű integrálást tesz lehetővé a g(x) = f '(x)/f(x) formájú függvények esetében: g(x) antideriváltja: ln(|f(x)|). Ez a láncszabály, és a következők miatt van így:
más szavakkal:
és
Néhány gyakorlati példa: Ha g(x) = tan(x):
Ha f(x) = cos(x) and f'(x)= – sin(x):
ahol C egy tetszőleges integrálási állandó
Legyen:
ekkor:
Numerikus érték számolása[szerkesztés]
Az elektronikus kalkulátorok megjelenése előtt az ln(1 + x) kiszámítása sorbafejtéssel egy adott pontosságig elvégezhető volt. Az elektronikus kalkulátorok és a számítógépek elterjedésével, ezt a számítást a gép pillanatok alatt elvégzi, ahol a program az eredeti sorbafejtést végzi.
A természetes logaritmus kiszámítására a Taylor-sor írható, mint:
A következő azonossággal a konvergencia gyorsítható:
feltéve, hogy y = (x−1)/(x+1) és Re(x) ≥ 0 de x ≠ 0.
Ha x > 1, akkor minél közelebb van x értéke 1-hez, annál gyorsabb a konvergencia. A logaritmus azonosságai ezt jobban megvilágítják:
10 természetes logaritmusa[szerkesztés]
A 10 természetes logaritmusa (közelítő értéke 2,30258509...,[13]) például a természettudományos számításoknál hasznos, ahol természetes logaritmust normálalakban ábrázolják: mantissza szorozva 10 hatványaival:
Ezzel az algoritmussal az összes pozitív valós szám logaritmusa redukálható természetes logaritmusra a tartományban.
Nagy pontosságú számítás[szerkesztés]
Nagy pontosságú számításra a Taylor-sor nem használható, mert igen lassan konvergáló sorozat. Erre a célra az 1-hez közeli számok esetén a Newton-módszer használható, mely sokkal gyorsabban konvergál. Ez kihasználja, hogy a logaritmus inverze exponenciális függvény. Az iteráció erre egyszerűsödik:
ami köbösen konvergál ln(x)-hez.
Egy igen nagy pontosságú formula:[14] [15]
ahol M 1 és 4/s számtani-mértani közepe, és
ahol úgy választják m-et, hogy p bites pontosságot elérjen. A legtöbb célra m = 8 elég. Ezzel a módszerrel és a Newton-módszerrel az exponenciális függvény értéke is kiszámítható. Ehhez elég gyorsan konvergáló sorozatokkal a szükséges irracionális konstansok megfelelő pontossággal előzetesen számíthatók.
Számítási bonyolultság[szerkesztés]
A természetes logaritmus értékének számítási bonyolultsága számtani-mértani közép használatával O(M(n) ln n), ahol n a kívánt pontos jegyek száma, és M(n) két n jegyű szám összeszorzásának számítási bonyolultsága.
Lánctörtek[szerkesztés]
A logaritmus nem írható fel egyszerű lánctört alakban, de általánosított lánctörtként már igen:
Ezek a lánctörtek gyorsan konvergálnak 1-hez közeli értékekre, különösen az utolsó. A nagyobb számok természetes logaritmusa ezek összeadásával számítható.
Például, mivel 2 = 1,253 × 1,024, a 2 természetes logaritmusa kiszámítható így:
Továbbá, mivel 10 = 1,2510 × 1,0243, hasonlóan:
Komplex logaritmus[szerkesztés]
Az exponenciális függvény kiterjeszthető a teljes komplex síkra, mint ex; ehhez használható a sorfejtés komplex x helyekre. Ennek az inverze a komplex természetes logaritmus. Ekkor két probléma adódik: az egyik, hogy nincs olyan véges x szám, amire ex = 0, továbbá e2πi = 1 = e0, vagyis a logaritmus nem egyértelmű. Ez abból adódik, hogy ez nem injektív a teljes komplex síkon, sőt periodikus, ez = ez+2nπi, minden komplex z helyre és n egész számra.
Így a logaritmus nem terjeszthető ki a teljes komplex síkra, és nem függvény, hanem többértékű reláció, aminek az egy helyen felvett értékei 2πi egész számú többszöröseivel különböznek egymástól. Csak egy ága lehet egyértelmű, és ezt egy felvágott komplex síkon lehet értelmezni. Például, ln i = 1/2 πi vagy 5/2 πi vagy −3/2 πi, satöbbi; és habár i4 = 1, 4 log ilehet 2πi, vagy 10πi vagy −6 πi, és így tovább.
- A természetes logaritmus főágának grafikonjai
-
z = Re(ln(x+iy))
-
z = Im(ln(x+iy))
-
z = ln(x+iy)
-
Az előző három grafikon szuperpozíciója
Irodalom[szerkesztés]
- Reiman istván: Matematika). (hely nélkül): Typotex Kft. 2011. ISBN 9789632793009
- Gerőcs L.-Dr.Vancsó Ödön: Matematika). (hely nélkül): Akadémia Kiadó Zrt. 2010. ISBN 9789630584883
- Sasaki, T.; Kanada, Y: "Practically fast multiple-precision evaluation of log(x)"). (hely nélkül): Journal of Information Processing 5 (4). 2011.
További információk[szerkesztés]
- http://betterexplained.com/articles/demystifying-the-natural-logarithm-ln/
- http://ci.nii.ac.jp/naid/110002673332
Kapcsolódó szócikkek[szerkesztés]
- Logaritmus
- Euler-féle szám
- Leonhard Euler
- Hatvány
- Izomorfia
- Taylor-sor
- Mercator-sor
- Newton-módszer
- Láncszabály
- Integrálási állandó
Források[szerkesztés]
- ↑ Mathematics for physical chemistry, 3rd, Academic Press, 9. o. (2005). ISBN 0-125-08347-5, Extract of page 9
- ↑ J J O'Connor and E F Robertson: The number e. The MacTutor History of Mathematics archive, 2001. szeptember 1. (Hozzáférés: 2009. február 2.)
- ↑ Cajori, Florian. A History of Mathematics, 5th ed. AMS Bookstore, 152. o. (1991). ISBN 0821821024
- ↑ R. P. Burn (2001) "Alphonse Antonio de Sarasa and Logarithms", Historia Mathematica 28:1 – 17
- ↑ Flashman, Martin: Estimating Integrals using Polynomials. [2012. március 26-i dátummal az eredetiből archiválva]. (Hozzáférés: 2008. március 23.)
- ↑ Boyers, Carl. A History of Mathematics. Wiley (1968)
- ↑ Harris, John (1987). „Australian Aboriginal and Islander mathematics” (PDF). Australian Aboriginal Studies 2, 29–37. o. [2007. augusztus 31-i dátummal az eredetiből archiválva]. (Hozzáférés: 2008. február 12.)
- ↑ Large, J.J. (1902). „The vigesimal system of enumeration”. Journal of the Polynesian Society 11 (4), 260–261. o. [2019. február 1-i dátummal az eredetiből archiválva]. (Hozzáférés: 2011. március 30.)
- ↑ Cajori, Florian (1922). „Sexagesimal fractions among the Babylonians”. American Mathematical Monthly 29 (1), 8–10. o. DOI:10.2307/2972914.
- ↑ Calculus: An Applied Approach, 8th, Cengage Learning, 331. o. (2007). ISBN 0-618-95825-8, Section 4.5, page 331
- ↑ Ballew, Pat: Math Words, and Some Other Words, of Interest. [2012. február 11-i dátummal az eredetiből archiválva]. (Hozzáférés: 2007. szeptember 16.)
- ↑ "Logarithmic Expansions" at Math2.org
- ↑
 A002392
A002392
- ↑ (1982) „Practically fast multiple-precision evaluation of log(x)”. Journal of Information Processing 5 (4), 247–250. o. (Hozzáférés: 2011. március 30.)
- ↑ (1999) „Stacs 99” 1564, 302–312. o. DOI:10.1007/3-540-49116-3_28.
























































