Felületi feszültség




A felületi feszültség a folyadékok alapvető tulajdonsága, ami miatt a folyadékok a lehető legkisebb fajlagos felületű alakzatot (gömb) igyekeznek felvenni, ha külső erőtér nem hat rájuk. Oka a folyadék részecskéi (atomok, egyszerű és összetett ionok, molekulák vagy ezekből felépülő kisebb aggregátumok) között fellépő kohéziós erő. Ezért gömb alakú a kis méretű lebegő folyadékcsepp, vagy a szappanbuborék stb.
A felületi feszültség következménye, hogy bizonyos tárgyak és állatkák a vízben nem süllyednek el, a víz felületén maradnak, bár a sűrűségük nagyobb, mint a folyadéké.
A felületi feszültség magyarázata[szerkesztés]
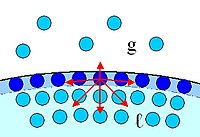
A felületi feszültség léte a molekuláris erőkkel függ össze.
A folyadékok határfelületi rétegében lévő alkotórészek más energetikai állapotban vannak, mint a folyadék belsejében lévők. Ennek oka az, hogy a folyadék felületén a kémiai és fizikai tulajdonságokat meghatározó mikrorészecskék környezetében a folyadék belseje felé azonos felépítésű folyadékmolekulák, míg a másik oldalon egy másik közeg, - például levegő - más tulajdonságú molekulái vannak. Így az aszimmetrikus erőhatások miatt nagyobb energiájú állapotban vannak, mint a folyadék belsejében elhelyezkedő, egymáshoz képest energetikailag kiegyensúlyozott társaik.
Tiszta anyagok esetén a felületi réteg felett az anyag gőz állapotú részecskéi találhatók, amelyben a részecskék átlagos távolsága lényegesen nagyobb – a vonzóerők lényegesen kisebbek –, mint a folyadék belsejében. A szomszédos molekuláktól származó kohéziós erők a folyadék belsejében kompenzálják egymást, a felületen viszont ezeknek az eredője a folyadék belseje felé mutat, amint azt a mellékelt ábra szemlélteti. Ez azt jelenti, hogy a kohéziós erő a felületi molekulákat a folyadék belseje felé igyekszik elmozdítani.
A kohéziós erők a felületre ún. kohéziós nyomást fejtenek ki, amelyet közvetlenül megmérni nem lehet, de közelítő számítások alapján ez a nyomás például víz esetében az atmoszferikus nyomás több ezerszeresét is eléri. Ez megmagyarázza, hogy a folyadékok összenyomhatósága kicsi, hiszen külső hatás nélkül is összenyomott állapotban vannak.
Ennek az aszimmetrikus erőhatásnak a mértéke a felületi feszültség (jele γ, vagy σ), amely az anyagokra jellemző intenzív fizikai mennyiség. Még pontosabban nem csak az adott folyadékra, hanem a fent leírt aszimmetrikus erőhatásokból eredően a két érintkező réteg határfelületére jellemző mennyiség. Más a felületi feszültsége például a víznek levegővel érintkezve, illetve ha étergőz van a felszín felett. Mivel legtöbbször a levegő-folyadék érintkezése fordul elő, ezért a felületi feszültségre jellemző adatokat - ha más megjelölés nincs - a levegő-folyadék határfelületre szokták megadni.
Az elnevezése csak részben helytálló, ugyanis nem feszültség jellegű mennyiség, hanem mint a definíciós összefüggésből kitűnik: a felületben, annak egységnyi hosszúságú vonalában ható erővel (N/m), vagy egységnyi nagyságú felület létrehozásához szükséges munkával (J/m²), az ún. felületi munkával egyenlő.
A felületi munka[szerkesztés]

Ahhoz, hogy a folyadék belsejéből molekulákat juttassunk a felszínre, ezáltal a felszín dA-val növekedjék, a felszínt kifeszítő erők ellenében dw munkát kell végeznünk. (Emiatt nagyobb a felszínen lévő részecskék helyzeti energiája, mint a folyadék belsejében lévőké.)
A felület valamely ℓ hosszúságú vonala mentén, arra merőlegesen a szomszédos részecskék között F erő hat, amely ellenében ℓdx =dA új felület létrehozásához Fdx = dw munka befektetése szükséges:
- , mértékegységei:
Azt is mondhatjuk: a felületi feszültség a (saját gőzével érintkező) folyadék egységnyi felületének energiatöbblete a folyadék belsejéhez képest.
Néhány anyag felületi feszültsége[szerkesztés]
| Néhány anyag felületi feszültsége levegőn[1][nincs a forrásban] | |||||
|---|---|---|---|---|---|
| anyag | Hőmérséklet, °C | Felületi feszültség, N·m−1=J·m−2 | anyag | Hőmérséklet, °C | Felületi feszültség, N·m−1=J·m−2 |
| Aceton | 20 | 23,7 | Metil-alkohol | 20 | 22,50 |
| Benzol | 30 | 27,56 | Oktán | 20 | 21,62 |
| Benzol | 20 | 28,88 | Pentán | 20 | 16,00 |
| Butil-acetát | 20 | 25,09 | Szén-tetraklorid | 25 | 26,43 |
| Dietil-éter | 25 | 20,14 | Toluol | 20 | 28,52 |
| Etilén-glikol | 25 | 47,3 | Víz | 20 | 72,86 |
| Etil-alkohol | 20 | 22,39 | Víz | 25 | 71,99 |
| Etil-alkohol | 30 | 21,55 | NaCl | 801 | 115 |
| Glicerin | 30 | 64,7 | Higany | 20 | 486,5 |
| Heptán | 20 | 20,14 | Higany | 25 | 485,5 |
| n-Hexán | 20 | 18,4 | Higany | 30 | 484,5 |
| Kloroform | 25 | 26,67 | Ón | 400 | 518 |
Nedvesítés[szerkesztés]

A folyadék molekuláira a felületet körülvevő más anyag molekulái is vonzóerőt fejthetnek ki – ez a jelenség az adhézió –, az ebből származó erő az adhéziós erő. Ha ezeknek az erőknek a folyadék molekuláira kifejtett hatása elhanyagolható (pl. levegő, g) a kohéziós erőkhöz képest, akkor a felületen lévő folyadékrészecskék a kohéziós erők hatására a folyadék belseje felé igyekeznek elmozdulni, vagyis a felület valóban csökkenni igyekszik. Ha ezeknek az erőknek a folyadék (ℓ) molekuláira kifejtett hatása nem hanyagolható el – például egy szilárd (s) felületen helyezkedik el –, akkor a folyadék jobban, vagy kevésbé terül szét azon, nedvesíti, vagy kevésbé nedvesíti azt, attól függően, hogy a vonzó (vagy taszító) erők mekkorák.

A nedvesítés mértékét a nedvesítési peremszöggel (Θ) jellemezzük. Ha a peremszög kisebb mint 90°, akkor részleges nedvesítésről, ha nagyobb 90°-nál, akkor részleges nem nedvesítésről beszélünk.
A közös határon fellépő erőket a határfelületi feszültséggel jellemezzük (γsg, γℓs, γℓg). Értelmezése hasonló a felületi feszültségéhez, csak itt a kohéziós erőkön kívül az adhéziós erők is közreműködnek. A folyadék addig terül a felületen, amíg az erőegyensúly beáll. Az erőegyensúly feltétele (Young-egyenlet):
A nedvesítés mértékét ezeknek a határfelületi feszültségeknek a módosításával lehet befolyásolni. A mosószerek a folyadék és a szilárd fázis közötti határfelületi feszültség megváltoztatásán keresztül fejtik ki a hatásukat. Más esetben a szilárd test felületkezelésével változtatható meg a nedvesítés mértéke.
Kapilláris emelkedés és kapilláris süllyedés[szerkesztés]


Úgyszintén a felületi feszültséggel függ össze az ún. kapilláris emelkedés és kapilláris süllyedés jelensége.
Kapillaritás hajszálcsövekben[szerkesztés]
A vékony csövekben (hajszálcsövekben, latin eredetű kifejezéssel kapillárisokban) a folyadékok nem követik a közlekedőedényekre vonatkozó törvényt: a nedvesítő folyadék szintje magasabb, a nem nedvesítő folyadéké pedig alacsonyabb, mint nagy felületű edényben. Az előbbi jelenséget kapilláris emelkedésnek, utóbbit kapilláris süllyedésnek, az egész jelenségkört pedig hajszálcsövességnek (kapillaritásnak) nevezzük. Üvegcsőben például a víz kapilláris emelkedését, illetve a higany kapilláris süllyedését lehet megfigyelni. Kapilláris emelkedés akkor következik be, ha a folyadék nedvesíti a kapilláris falát, vagyis a folyadék és a szilárd anyag részecskéi között nagyobb a vonzóerő, mint a folyadék molekulái között. A nedvesítési peremszög ilyenkor Θ < 90°. Ha a folyadék és a szilárd anyag részecskéi között kisebb a vonzóerő, mint a folyadék molekulái között, akkor kapilláris süllyedés lép fel. A nedvesítési peremszög ebben az esetben Θ > 90°.
A mellékelt ábra alapján kiszámíthatjuk az emelkedés, illetve a süllyedés nagyságát. Ha például a nedvesítő folyadék a csőben h magasságba emelkedik fel, akkor a folyadékoszlopra ható nehézségi erő (Fneh):
Az üveg részecskéi között működő adhéziós erő felfelé mutató komponense (Fγ):
A folyadékoszlop egyensúlyban van, tehát a két erő egyenlő nagyságú (de ellentétes irányú):
Ebből a folyadék emelkedésének vagy süllyedésének mértéke, a h kiszámítható:
Kapillaritás keskeny résekben[szerkesztés]
A hajszálcsövekhez hasonlóan a keskeny résekben is megfigyelhető a kapilláris emelkedés és a kapilláris süllyedés. A jelenség egyszerűen tanulmányozható például két olyan üveglap között, amelyek egy közös, függőleges helyzetű élben találkoznak és kis szöget zárnak be egymással. Ha a két lap alsó részét vízbe merítjük, akkor a két üveglap közti térrészben a víz annál magasabbra emelkedik, minél kisebb az üveglapok távolsága. Mérésekkel és elméleti úton is igazolható, hogy a lapok közti távolság (d) és az emelkedés magassága (h) fordítottan arányos egymással. A fordított arányosság miatt az üveglemezek közti térrészben a víz felszíne egy hiperbola mentén helyezkedik el.
- A víz kapilláris emelkedése üveglapok között
A felületi feszültség hőmérsékletfüggése[szerkesztés]

A tiszta folyadékok felületi feszültsége csökken a hőmérséklet növekedésével. A kritikus hőmérsékleten megszűnik a folyadék és annak gőze közötti különbség, a fázishatár is eltűnik, a felületi feszültség nullára csökken. A felületi feszültség hőmérséklettel való változásából következtetni lehet a folyadék állapotbeli molekulák állapotára. A T hőmérsékleten mért felületi feszültség, a folyadék moláris térfogata és a hőmérséklet között az alábbi összefüggés áll fenn:
ahol
- Vm a folyadék moláris térfogata, m³/mol,
- γ a folyadék felületi feszültsége, N/m
- T a hőmérséklet, K
- Tc az anyag kritikus hőmérséklete, K
- k az Eötvös-féle állandó, J/(K mol2/3)
Ez a kifejezés az Eötvös-szabály. Az ún. normális folyadékok esetén az Eötvös-féle állandó értéke 2,1 x 10 -7 J/(K mol2/3).
A legtöbb folyadék esetében a felületi feszültség már 6 °C-kal a kritikus hőmérséklet alatt gyakorlatilag nulla, ezért az Eötvös-szabály alábbi alakja pontosabb eredményt ad:
A V2/3 mennyiség a folyadék 1 móljának a felületével arányos (mólfelület), ezért a γV2/3 szorzatot mólfelületi energiának nevezzük. Ez arányos annak a munkának a nagyságával, amely ahhoz szükséges, hogy 1 mólnyi folyadéknak megfelelő felületet létrehozzunk, vagyis 1 mól folyadékot teljes mértékben szétterítsünk.
Néhány anyag Eötvös-féle állandója[szerkesztés]
| Néhány anyag Eötvös-féle állandója [2] | |||
|---|---|---|---|
| Anyag | Eötvös-féle állandó, *10−7 J/(K mol2/3) | Anyag | Eötvös-féle állandó, *10−7 J/(K mol2/3) |
| Nitrogén | 2,00 | Metil-alkohol | 0,7-1,10 |
| Oxigén | 1,92 | Etil-alkohol | 0,9-1,3 |
| Klór | 2,10 | Fenol | 1,3-1,9 |
| szén-tetraklorid | 2,11 | Hangyasav | 0,6-1,1 |
| Benzol | 2,10 | Ecetsav | 0,9-1,3 |
| Dietil-éter | 2,17 | Trisztearin | 5,3-6,8 |
| Víz | 0,9-1,2 | ||
Folyadékok szerkezete[szerkesztés]
Az adatokból az látható, hogy több, nagyon különböző kémiai tulajdonságú folyadék Eötvös-állandója jó közelítéssel valóban 2,1. Vannak azonban olyan folyadékok is, amelyek nem követik ezt a szabályt, hanem k értéke jóval kisebb 2,1-nél, és értéke változik a hőmérséklettel, ezért van k-ra egy intervallum megadva a táblázatban. Ilyen anyag a víz, amely nagyon sok szempontból kivétel, de az alkoholok és a savak is. Ezen anyagok molekulaszerkezetében van közös rész, nevezetesen az -OH csoport.[2]
Az Eötvös-féle állandó kisebb értékét úgy értelmezik, hogy ezeknek az anyagoknak folyékony halmazállapotban más a moláris tömegük, mint gőz halmazállapotban, mégpedig folyékony halmazállapotban nagyobb, mint gőz állapotban. A víz, a savak és az alkoholok folyékony halmazállapotban összekapcsolódott részecskékből, rövid távon rendezett halmazokból – asszociált molekulákból – állnak. Ez a kapcsolat azonban nem annyira állandó, mint egy vegyület molekulája esetében, hanem változó nagyságú, rendezett körzetek kialakulásáról van szó, amelyek folyamatosan keletkeznek és felbomlanak.
Egyes folyadékok – amelyek részecskéi viszonylag hosszúak – Eötvös-féle állandója nagyobb, mint 2,1. Ezek a hosszú molekulák a felületen egymással párhuzamosan és hossztengelyeikkel a felületre merőlegesen helyezkednek el. Ebben az elrendezésben a részecskék kevesebb helyet foglalnak el, mintha rendezetlenül helyezkednének el, vagy pedig gömb alakúak volnának. Ezek a folyadékok tehát a felületi feszültség szempontjából úgy viselkednek, mintha a moláris térfogatuk kisebb lenne a moláris tömegüknek megfelelő értéknél.
A felületaktív anyagok. Miért mos a mosószer?[szerkesztés]

A felületaktív anyagok – tenzidek vagy detergensek – az oldószer, például a víz felületi feszültségét csökkentik azáltal, hogy molekuláik a folyadék felületén irányítottan helyezkednek el. Az ilyen tulajdonságú anyagok – ún. amfipatikus jellegű vegyületek – egy hosszabb szénláncú liofób (vízre vonatkoztatva hidrofób) csoportot és liofil (vízre vonatkoztatva hidrofil) atomot, vagy rövid atomcsoportot tartalmaznak. A hagyományos szappan is ilyen szerkezetű: hosszú szénláncú, természetes eredetű zsírsavak nátriumsói.
A mosószerek legfontosabb tulajdonsága a mosóhatásuk szempontjából, hogy csökkentik a felületi feszültséget. Ugyanis a víz a nagy felületi feszültsége miatt a textilszövet finom pórusaiba nem képes behatolni, ezért onnét például a zsíros szennyeződést sem tudná eltávolítani. Szappan – és más, ma használatos nagy hatású mosószerek – segítségével azonban képes erre. A detergens részecskék a zsír és a víz közötti közös határrétegbe úgy épülnek be, hogy a hidrofób részük benyúlik a zsírcsepp belsejébe, a hidrofil pedig a vízbe. Mozgatással a zsírcseppek elszakadnak a textil felületétől és emulziót képeznek.
Mérési módszerek[szerkesztés]

Folyadék halmazállapotú rendszerek felületi (határfelületi) feszültségének mérésére többféle módszer is kínálkozik,[3] mint pl.
- a kapilláris emelkedés módszere,
- a buboréknyomásos módszer,
- a sztalagmométeres módszer,
- a kiszakításos módszer és
- a nyugvó csepp módszer, főként nagyhőmérsékleten, például fémolvadék esetén.
Kapilláris emelkedés és kapilláris süllyedés[szerkesztés]
A kapilláris emelkedés (süllyedés) módszerével a felületi feszültség meghatározását a folyadékba merülő r sugarú kapillárisban h magasra emelkedő (vagy mélyre süllyedő) folyadék hidrosztatikai nyomásának mérésére vezetjük vissza. A ρ sűrűségű folyadékoszlop súlya egyensúlyt tart a meniszkusznál fellépő adhéziós erővel. A fentebb már levezetett összefüggésből a felületi feszültségre az alábbi egyenlet adódik:
Az egyenletben:
- γ a felületi feszültség, N·m−1
- r a kapilláris sugara, m
- ρ a folyadék sűrűsége, kg·m−3
- h a kapilláris emelkedés (süllyedés), m
- Θ a kapilláris és a folyadék közötti nedvesítési peremszög.
A buboréknyomásos módszer[szerkesztés]

A buboréknyomásos módszerrel azt a külső nyomást mérjük, amely szükséges ahhoz, hogy a mérendő felületi feszültségű folyadékba h mélységre bemártott r sugarú kapilláris végén buborék képződjék. Ez a nyomás a pγ kapilláris nyomás. Ha a buborék r sugarát dr-rel megnöveljük, a buborék térfogata 4π r²dr-rel, felülete pedig 8πrdr -rel nő meg. A közben végzett térfogati munkának egyenlőnek kell lennie a felületi feszültség munkájával:
amiből a felületi feszültség:
Lassú buborékolás esetén a kapilláris végén képződő buborékban kialakuló nyomás (pγ) és a kapilláris bemerüléséből származó hidrosztatikai nyomás (ph) összege azonos az edényben levő nyomás és a külső légnyomás közötti különbséggel (pm), amit a manométerrel mérünk, vagyis:
A vizsgált folyadék felületi feszültsége a
kifejezéssel számítható.
Az összefüggésekben:
- pγ a kapilláris nyomás, Pa
- γ a felületi feszültség, N·m−1
- r a kapilláris sugara, m
- ρv a folyadék sűrűsége, kg·m−3
- hv a kapilláris bemerülési mélysége, m
- rm a manométerfolyadék sűrűsége, kg·m−3
- hma manométerfolyadék maximális nívókülönbsége, m
- g a nehézségi gyorsulás, 9,81 m·s−2
A kapilláris sugarának közvetlen mérése nehézkes, ezért azt ismert felületi feszültségű folyadékban (pl. vízben) kialakult nyomáskülönbség mérése útján lehet meghatározni.
A víz hőmérséklettől függő felületi feszültsége t °C-on a
egyenletből számítható ki. Ennek ismeretében a kapilláris sugara az:
összefüggésből adódik.
A buboréknyomásos módszerrel nem csak felületi feszültség mérhető, hanem – ha ismert a felületi feszültség – a kapillárist két különböző mélységbe bemerítve a vizsgálandó folyadék sűrűsége is meghatározható.
A sztalagmométeres módszer[szerkesztés]
A sztalagmométeres módszer elve azon alapszik, hogy a folyadék a speciálisan kialakított pipettából, a sztalagmométerből lassan kicsepegve a felületi feszültségétől és a sűrűségétől függő nagyságú cseppeket képez. A csepp leszakadása éppen akkor következik be, amikor a növekvő csepp súlya (mog = voρog) egyenlő lesz a sztalagmométer tárcsaszerűen kiképzett r sugarú, alsó csiszolt korongján működő felületi erővel: (2rπγo). A felületi feszültség a V térfogatú pipettában lévő oldat kicsepegtetésekor észlelt cseppszámából (no) az alábbi módon számítható:
ill. víz esetén:
amelyből az oldat felületi feszültsége:
Az összefüggésekben:
- no a vizsgált oldat cseppszáma,
- nv a víz cseppszáma,
- r a sztalagmométer korongjának a sugara, m
- γo a vizsgált oldat felületi feszültsége, N·m−1
- γv a víz felületi feszültsége, N·m−1
- ρo az oldat sűrűsége, kg·m−3
- ρv a víz sűrűsége, kg·m−3
- g a nehézségi gyorsulás, 9,81 m·s−2
- k a sztalagmométer állandója
- V a sztalagmométer térfogata, m³
A sztalagmométer állandóját desztillált víz felületi feszültségének ismeretében, vízzel végzett kísérlet alapján kell meghatározni.
A kiszakításos módszer[szerkesztés]


A kiszakításos módszer annak az erőnek a mérésén alapszik, amely egy vékony, R sugarú, gyakran platina-irídium ötvözetből készült gyűrűnek a vizsgált folyadékból történő kiemelése közben, a folyadék felületéről való kiszakításához szükséges (Du Noüy gyűrűs módszere). A gyűrű kiszakadása akkor következik be, amikor az Fo húzóerő éppen meghaladja a kör alakú gyűrű kerületén – a két folyadékfilmben – működő felületi erőt, vagyis amikor:
amelyből az oldat felületi feszültsége:
Az F erő mérésre ún. torziós mérleg alkalmas, amelyet mérés előtt ismert felületi feszültségű folyadékkal – célszerűen például desztillált vízzel – kalibrálni kell, ezt követően közvetlenül mérhető a folyadék felületi feszültsége. Másik módszer szerint egy műszerállandót (k) kell meghatározni, és a mérési eredményt az alapján korrigálni, mivel víz esetében:
a két összefüggésből pedig
amely összefüggésekben
- R a Pt-Ir-gyűrű sugara, m
- γo a vizsgált oldat felületi feszültség, N·m−1
- γv a víz felületi feszültsége, N·m−1
- Fo az oldatból történő kiszakításhoz szükséges erő, N
- Fv a vízből történő kiszakításhoz szükséges erő, N
- k a műszerállandó, m−1
A nyugvó csepp módszer[szerkesztés]

A nyugvó csepp módszere egy sík, szilárd felületen elhelyezkedő folyadékcsepp alakjának megfigyelésén alapul. Az egyensúlyba került folyadékcseppről fénykép készül és a felvételről lemérhető a kialakult nedvesítési peremszög is. A határfelületi feszültségek meghatározzák a kialakult olvadékcsepp geometriai jellemzőit, ezért az olvadékcsepp alakját jellemző paraméterekből számítható az olvadék felületi feszültsége, jó közelítéssel az alábbi összefüggéssel:
A kifejezésben:
- γlg az olvadék felületi feszültsége, J/m² ,
- ρ az olvadék sűrűsége, kg/m³ ,
- g a gravitációs állandó, 9,81 m/s² ,
- X a csepp legnagyobb horizontális mérete, m,
- Z a csepp legnagyobb vertikális mérete, m.
A nyugvó csepp módszer megvalósításához szükséges berendezés vízszintes csőkemencéből áll, amelyben egy vízszintes síkon elhelyezhető a vizsgálandó kerámialap és rajta a vizsgálandó fémdarab (minta). A műszer optikai rendszerrel, hőmérsékletmérésre szolgáló termoelemmel, vákuumrendszerrel és a folyadékcsepp alakjának rögzítésére szolgáló fényképezőgéppel van ellátva.
Jegyzetek[szerkesztés]
- ↑ Lásd: Felületi feszültség értékek
- ↑ Erdey-Grúz Tibor: Fizikai kémia alapjai. Műszaki Könyvkiadó, Budapest, 1963.
- ↑ Fizikai-kémiai laboratóriumi gyakorlatok. Szerkesztette: Dr. Báder Imre. Miskolci Egyetemi Kiadó. Miskolc,1998.
Források[szerkesztés]
- http://www.avasi.hu/sites/default/files/tartalom/agymenok/feluleti_feszultseg_formikusok_2017.pdf
- http://www.fizikakonyv.hu/063.pdf
- https://tudasbazis.sulinet.hu/hu/szakkepzes/vegyipar/fizikai-kemia/a-folyadekok/a-feluleti-feszultseg-fogalma-a-feluleti-feszultseget-befolyasolo-tenyezok
- http://fizika.fazekas.hu/wp-content/uploads/pdf/7.osztály_Felületi-feszültség.pdf?_t=1588839905
Kapcsolódó szócikkek[szerkesztés]

































