Integrál

Az integrál a matematikai analízis fontos fogalma. Egy adott f valós, [a, b] intervallumon definiált függvény határozott integrálja ugyanezen intervallumon:
Egyszerűen úgy fogalmazható meg, hogy ez a függvény és az x-tengely által az ([a, b] intervallumon) bezárt előjeles terület.
Ezt a területet a következők határolják:
- az f függvény grafikonja,
- az x-tengely
- x = a és az x = b függőleges egyenesek
Az x-tengely feletti terület "hozzáad" a teljes területhez, vagyis pozitív területű, míg az x-tengely alatti terület "elvesz" a teljes területből, vagyis negatív területű.
Az integrálás a deriválás ellentétének tekinthető, emiatt néha az integrál kifejezést használják az antiderivált (f antideriváltjai azok a függvények, amelyek deriváltja f) jelölésére is.
Amennyiben nincs meghatározva az integrálás tartománya, akkor határozatlan integrálról beszélünk:
Ez a szócikk a határozott integrálról szól.
Az integrálás alapjait egymástól függetlenül fedezte fel Newton és Leibniz a 17. század végén. A mindkettőjük által felfedezett Newton–Leibniz-tétel összeköti az integrálást és a deriválást:
ha f egy folytonos valós függvény az [a, b] intervallumon akkor, ha adott az F függvény, ami f primitív függvénye, akkor f határozott integrálja a következőképpen számítható ki:
Az integrálás és a deriválás a fizikusok és a mérnökök fontos eszköze. Az analízis megalkotói az integrált úgy képzelték el, mint olyan közelítő téglalapok területösszege, amelyek alapterülete infinitezimális. Az integrál egyik első és legelterjedtebb formális definíciója Bernhard Riemanntól származik. Ez a definíció egy közelítés (Riemann-összegek) határértékeként definiálja az integrál értékét. A 19. század elején az integrálfogalom különféle általánosításai jelentek meg, amelyek az integrálható függvények halmazát kiterjesztették, éppúgy, mint ahogy kiterjesztették ezen integrálható függvények lehetséges alaphalmazát. A vonalintegrál olyan integrál, ahol az integrálási tartomány nem egy intervallum, hanem egy meghatározott görbe, amely összeköt két pontot egy síkon vagy a térben. Az integrál ilyen általánosításainak legfőbb mozgatórugója a fizika, különösen az elektrodinamika szükségletei voltak. Többféle modern integrál is létezik, a legismertebb talán a Lebesgue-integrál, amit Henri Lebesgue fejlesztett ki a 20. század elején.
Történet[szerkesztés]
Első megjelenés[szerkesztés]
Az első dokumentált szisztematikus módszer határozott integrálok meghatározására a görög Eudoxosz úgynevezett kimerítési módszere volt, amellyel területeket és térfogatokat lehet kiszámolni, úgy, hogy ezeket felbontjuk végtelen sok olyan alakzatra, amelyek térfogatát/területét ismerjük. Ezt a módszert később Arkhimédész fejlesztette tovább, és használta parabolák területének kiszámolására és a kör területének közelítő meghatározására. Hasonló módszerek Kínában is megjelentek, hasonlóan a kör területének meghatározása közben. Később ezt a módszert Kínában a gömb térfogatának meghatározásához is használták. (Shea 2007; Katz 2004, pp. 125–126).
A következő jelentős állomás a 16. században érkezett Bonaventura Cavalieritől a Cavalieri-elv formájában. Cavalieri meghatározta az xn integrálját egészen n = 9-ig. A következő lépés a 17. század elején következett, amikor Isaac Barrow és Evangelista Torricelli elsőként rámutattak arra, hogy a differenciálszámítás és az integrál között kapcsolat lehet. Barrow megadta az első bizonyítást a Newton–Leibniz-tételre. Wallis általánosította Cavalieri módszerét a negatív kitevőkre és törtkitevőkre is.
Newton és Leibniz[szerkesztés]
A legjelentősebb fejlődés az integrálásban a 17. században következett be a Newton–Leibniz-tétel felfedezésével. A tételt két matematikus, Newton és Leibniz egymástól függetlenül egyszerre fedezte fel. A tétel rámutat a differenciálszámítás és az integrálás közötti kapcsolatra. Ezt a kapcsolatot és a differenciálszámításban szerzett korábbi tapasztalatokat felhasználva lehetőség nyílt számos, különböző integrál kiszámítására. Ugyanakkor a Newton–Leibniz-tétel nem csak az integrálok kiszámítására használható, hiszen az a tény, hogy az integrálás valamilyen szempontból a deriválás "ellentéte", más problémák megoldása felé is megnyitotta az utat. Ezen kezdeti lépések még az infinitezimálisokat alkalmazták a definíciókban. Az ekkor, Leibniz által kifejlesztett jelölés vált az általánossá az integrálás jelölésére.
Az integrál formalizálása[szerkesztés]
Habár a Newton és Leibniz által felfedezett formula általános módszert szolgáltatott integrálok kiszámításához, mindkettőjük munkájából hiányzott a matematikai formalizmus. Az analízis szigorú megalapozására a határérték megjelenése adott lehetőséget. Az integrálás határértékkel való pontos matematikai definícióját először Riemann adta meg. Habár bármely folytonos függvény Riemann-integrálható, léteznek olyan nem folytonos függvények is, amelyek szintén Riemann-integrálhatóak. Később például a Fourier analízishez kapcsolódóan általánosabb függvények is előkerültek, amelyekkel a Riemann-féle definíció nem tudott mit kezdeni, így később Lebesgue adott egy integráldefiníciót, amely a mértékelméleten alapul.
Jelölések[szerkesztés]
Newton vagy egy kis függőleges egyenest használt a kifejezések felett az integrálás jelölésére, vagy bekeretezte a kifejezést. A függőleges vonal könnyen összetéveszthető volt a vagy a jelöléssel, amit Newton a deriváltak jelölésére használt, míg a bekeretezéses jelölés a könyvnyomtatás során okozott nehézségeket, így egyik jelölés sem terjedt el széles körben.
A mai jelölés az integrálásra 1675-ből, Leibniztől származik (Burton 1988, p. 359; Leibniz 1899, p. 154). A jelölésre Leibniz az ∫ integráljelet használta, amely az ſ (hosszú s) jelből származik, a szumma (latinul: ſumma; jelentése: "összeg") szó rövidítéseként. A mai jelölés Joseph Fourier-vel nyerte el a végső formáját, aki az integrálási határokat az integráljel alatt és felett kezdte jelölni az 1819–20-as Mémoires című könyvében (Cajori 1929, pp. 249–250; Fourier 1822, §231).
Elnevezések és jelölések[szerkesztés]
Egy valós f(x) függvény integrálja az x változóra nézve:
Az integráljel ∫ jelöli az integrálást. A dx jelöli, hogy az x változó szerint integrálunk. A ∫...dx jelölés belsejében található az integrandus, vagyis az integrálandó kifejezés. Ha nincs megadva integrálási tartomány/görbe/határok, akkor a jelölés a határozatlan integrált jelenti.
Egy adott halmaz fölötti integrálás esetén határozott integrálról beszélünk. Egy D halmaz fölötti integrált a következőképpen jelölünk: vagy , ha a halmaz az [a, b] intervallum. A D halmaz vagy az [a, b] intervallum az úgynevezett integrálási tartomány.
Ha egy függvénynek létezik az integrálja, akkor integrálható.
Az integrálási változót jelölő dx-nek többféle értelmezése is lehetséges, attól függően, hogy milyen fajta integrálról beszélünk. Vehetjük, úgy, mint csupán egy jelölést az integrálási változó használatára, vagy például a Riemann-összegeknél a téglalapok egyik oldalának az elfajult hosszának, a Lebesgue-integrál esetén dx jelöli az integrálásnál használt mértéket, míg a nemsztenderd analízisben, infinitezimálisnak tekinthetjük, vagy akár értelmezhetjük úgy, mint egy differenciál. Eredetileg Leibniz szerint infinitezimális változót jelöl, habár Leibniz értelmezése nem formális és nem megfelelően definiált, mégis ez az értelmezés nagyon elterjedt.
Bevezetés[szerkesztés]
Az integrálok nagyon sok helyzetben megjelenhetnek. Ha adott egy szögletes, téglatest alakú úszómedence, akkor könnyen megállapíthatjuk a bele tölthető víz térfogatát, felületét, a medence oldaléleinek hosszának összegét stb. Ha azonban a medencét lecseréljük egy például gömbölyű, lekerekített aljú medencére, akkor a fentiek kiszámításához már integrálra van szükségünk. Noha az eredményt jól közelíthetjük ilyen egyszerű példák esetén, de a mérnöki munkában, illetve a fizikában bizonyos esetekben a pontos eredmény elengedhetetlen.

Kezdésként vegyünk egy y = f(x) görbét x = 0 és x = 1 közötti intervallumon, úgy, hogy f(x) = √x. Ekkor megkérdezhetjük:
- Mekkora az f függvény alatti terület a 0-tól 1-ig terjedő intervallumon?
Nevezzük ezt az (egyelőre ismeretlen) területet f integráljának. Jelöljük ezt a következőképpen:
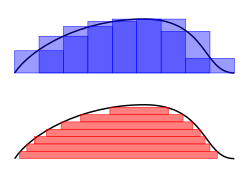
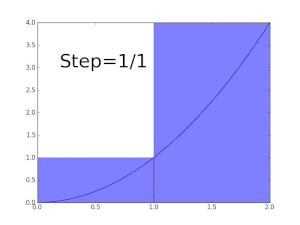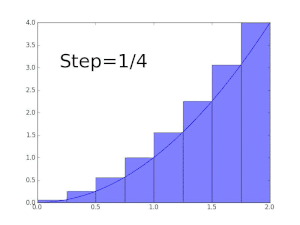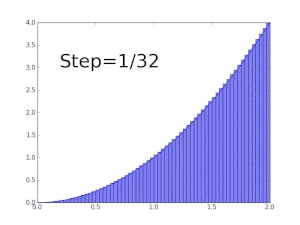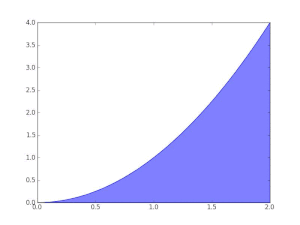
Első közelítésként vegyünk egy téglalapot az egységnyi hosszú intervallumon, vagyis amelynek oldalai x = 0 és x = 1. A monotonitás miatt a jobb szélen vett függvényértékű magasságú téglalap felső Darboux közelítő összeg lesz, míg a bal oldali pontban vett függvényértékű magasságú téglalap alsó Darboux közelítő összeg. Így adott, hogy az integrál értéke 1-nél kisebb pozitív valós szám. (Mivel az alsó közelítő téglalap területe 0, mivel a magassága 0, míg a felső közelítő téglalap területe 1 mivel a magassága f(1)=1). Nyilvánvalóan a közelítő téglalapok szélességének csökkentésével a közelítés pontossága javul. Ha az intervallumot 5 egyenlő részre osztjuk, következő közelítésnek, akkor az osztópontok a 0, 1/5, 2/5, és így tovább 1-ig lesznek. A felső közelítő téglalapok magassága az adott intervallumok jobb oldalában vett függvényértékek, vagyis √(1⁄5), √(2⁄5) és így tovább √1 = 1-ig. Ezen téglalapok területét összegezve kapjuk a következő, már pontosabb közelítést, ami:
Vagyis véges sok olyan szorzatot összegzünk, amelyek egyik tagja f egy pontbeli értéke, a másik tényező pedig két egymást követő osztópont különbsége (vagyis a téglalap alapjának a hossza). A fenti példában a közelítés még mindig nem megfelelő, így további osztópontok segítségével, több téglalap segítségével közelíthetjük a keresett területet, ugyanakkor belátható, hogy az ilyen közelítés soha nem lesz teljes pontosságú. A lényeges lépés a véges közelítő összegekről, véges szorzatok összegzéséről a megfelelő végtelen sok téglalap területének összegzésére való áttérés. (Önmagában a végtelen sok osztópont/intervallum nem biztosítja a pontos eredményt. A szükséges követelmény az, hogy minden osztópont közötti távolság 0-hoz tartson, vagyis a definíció a határértékre épül. Eredetileg a határérték-fogalom a mai formájában nem létezett, az csak később jelent meg, így az eredeti Newtoni-Leibnizi értelmezés az infinitezimális, vagyis a végtelen kicsiny hosszúságú alappal rendelkező közelítő téglalapok területösszegére épült, ugyanakkor ezek formalizálása nem bizonyult olyan egyszerűnek, mint amilyen szemléletes a jelentése. Így a későbbiekben az analízis fogalmait, így az integrált is a határérték fogalmára átültették.)
A gyakorlatban használatos módszert az integrálok értékének meghatározásához, a Newton-Leibniz-formula biztosítja, amely kapcsolatot teremt a deriválás és az integrálás között. Ha a fenti négyzetgyök-függvényre f(x) = x1/2-re alkalmazzuk, akkor azt kapjuk, hogy az f primitív függvénye vagy más néven antideriváltja az F(x) = (2/3)x3/2 függvény. Ennek segítségével az integrál pontos értéke a tétel szerint: F(1) − F(0), mivel a 0 és 1 az integrálási intervallum (a [0,; 1] intervallum) határpontjai. Vagyis:
(Ez egyébként egy általánosan is igaz szabály, vagyis, hogy az f(x) = xq, ahol q ≠ −1 függvény antideriváltja, amellyel az integrál pontos értéke kiszámítható, F(x) = xq + 1/(q + 1).)
Az
jelölés onnan ered, hogy az integrál végtelen sok szorzat összegeként volt definiálva (amelyek egyik tényezője minden esetben infinitezimális), és az összeg, summa, kezdőbetűje az angolban és a latinban az s betű. Az integrálási határok feltüntetése eredetileg nem volt Leibniz jelölésének része, ez később Fouriertől származik.
Újabban az infinitezimálisok újra megjelentek, most már kellően formalizálva a modern eszközök segítségével.
Formális definíciók[szerkesztés]


Az integrálok formális definíciójára több verzió is létezik, amelyek nem feltétlenül ekvivalensek. A különbségek nagy része azért van jelen mert így egyes függvények integrálhatóak egyes integrálokkal, míg más definíciót használva nem integrálhatóak. Bizonyos esetekben a különbségnek pedagógiai okai vannak. A leggyakoribb integrál definíciók (amelyek nem ekvivalensek) a Riemann és a Lebesgue-féle integrál definíciók. A Lebesgue-integrál a Riemann-integrál kiterjesztése, vagyis minden Riemann-integrálható függvény Lebesgue-integrálható is, és a két integrál értéke megegyezik.
De vigyázat, mert belefuthatunk olyan példába a későbbiekben, amely látszólag ellentmond eme állításnak. Elsőre úgy tűnhet, hogy az alábbi függvény Riemann-integrálható:
,
miközben nem Lebesgue-integrálható:
.
A hiba a terminus pongyola használatából adódik. A függvény improprius Riemann-integrálja létezik, de nem a Riemann-integrálja, amelyhez alapfeltétel a korlátos, zárt intervallum.
Riemann-integrál[szerkesztés]
A Riemann-integrált a Riemann-összegekkel definiáljuk. Egy függvény Riemann-összegéhez az integrálási intervallum úgynevezett címkézett partíciójára van szükségünk. Legyen [a, b] egy zárt valós intervallum; ekkor ennek az intervallumnak egy címkézett partíciójának a következő véges sorozatot nevezzük:
Ez felosztja az [a,b] intervallumot n db [xi−1, xi] részintervallumra úgy, hogy minden részintervallumhoz tartozik egy kijelölt pont ti ∈ [xi−1, xi]. Egy f függvény Riemann-összege a fenti címkézett partíció fölött:
vagyis egy olyan összeg, amelynek minden tagja egy közelítő-téglalap területe, amelynek magassága az adott intervallum kiválasztott pontjában vett függvényérték, míg a téglalap alapja az adott részintervallum, tehát az intervallum alapjának a hossza megegyezik az adott részintervallum hosszúságával. Δi = xi−xi−1 jelöli az i-edik részintervallum szélességét; míg a felosztás (partíció) finomságának a legnagyobb részintervallum hosszúságát nevezzük maxi=1…n Δi. Az f függvény Riemann-integrálja az [a,b] intervallumon S, ha:
- Bármely ε > 0-hoz, létezik egy δ > 0 úgy, hogy az [a,b] intervallum bármely címkézett felosztása amelynek finomsága kisebb, mint δ, olyan, hogy a fölötte vett Riemann-összeg maximum ε távolságra van S-től, vagyis:
- Vagyis:
- ahol a felosztás finomságát jelenti.
Ha minden részintervallumban a kiválasztott pont a függvény maximumértékét adja az adott intervallumon [illetve a minimumértékét], akkor a Riemann-összeg úgynevezett felső Darboux-összeg [illetve alsó Darboux-összeg], ami azt mutatja, hogy a két integrál (a Darboux-integrál és a Riemann-integrál) definíciója ekvivalens, illetve, hogy minden Darboux-integrálható függvény Riemann-integrálható függvény is és fordítva és az integrálok értéke mindig megegyezik.
Lebesgue-integrál[szerkesztés]
Gyakran felmerül az igény arra mind elméletben, mind pedig gyakorlati alkalmazásokban, hogy a Riemann-integrált kiterjesszük, általánosítsuk. Például a függvények egy olyan sorozata gyakran készíthető, amelyek közelítenek egy másik adott függvényt. Ekkor logikus, hogy az adott határfüggvény integrálja megegyezik a függvénysorozat integráljának határértékével. Ez ugyanakkor általánosan a Riemann-integrálra nem igaz mivel Riemann-integrálható függvények sorozatának határértéke lehet olyan függvény, amely nem Riemann-integrálható. A fenti tétel általánosan igazzá tehető, ha az integrál fogalmát általánosítjuk és így a lehetséges integrálható függvények halmazát kiterjesztjük. (Rudin 1987).
Ilyen kiterjesztés például a Lebesgue-integrál, ami arra a tényre épül, hogy ha függvényt az integrálási intervallumban átrendezzük, akkor az integrál értékének nem kellene változnia. Henri Lebesgue erre építve alkotta meg a róla elnevezett integrált, amit egy levélben így magyarázott el Paul Montelnek:
| „Ki kell fizetnem egy meghatározott összeget, amelyet összegyűjtöttem a zsebemben. Kivehetem az érméket és bankjegyeket olyan sorrendben, amilyenben csak akarom és ilyen sorrendben oda is adogathatom a célszemélynek addig, amíg el nem érem teljes kifizetendő összeget. Ez a Riemann-integrálnak felel meg. Ugyanakkor más sorrendben is fizethetek. Először is kiveszem az összes pénzt a zsebemből, ezután csoportosítom az érméket és a bankjegyeket az értékük szerint, majd a különféle a csoportokat egyenként adom át a célszemélynek. Ez az én integrálom.” |
- Forrás: (Siegmund-Schultze 2008)
Ahogy Folland (Folland 1984, p. 56) mondja, "Az f függvény Riemann-integrálásakor az adott [a, b] intervallumot particionáljuk részintervallumokra", míg a Lebesgue-integrál esetén, "az f függvény értékkészletét particionáljuk". A Lebesgue-integrál definíciója a μ mérték definíciójával kezdődik. A legegyszerűbb esetben a Lebesgue-mértéke egy A = [a,b] intervallumnak μ(A) az intervallum hossza, b − a, vagyis a Lebesgue-integrál értéke megegyezik a Riemann-integrállal ha mindkét integrál létezik. Bonyolultabb esetekben az a halmaz amit mérünk lehet, hogy nem összefüggő esetleg nagymértékben "szakadozott" és esetleg egyáltalán nem bontható fel intervallumokra.
Az "értékkészlet particionálás" elvét követve, egy nemnegatív f : R → R függvény integrálja az y = t és y = t + dt egyenesek közé eső területek összege minden t-re (vagyis a területet "vízszintes csíkokkal" daraboljuk fel, nem "függőlegesekkel"). Ez ilyen csík közé eső függvény alatti terület tehát: μ{ x : f(x) > t} dt. Legyen f∗(t) = μ{ x : f(x) > t}. Ekkor f Lebesgue-integrálja így definiált (Lieb & Loss 2001):
ahol az egyenlőség jobb oldalán álló integrál egy egyszerű improprius Riemann-integrál (az f∗ egy szigorúan csökkenő pozitív függvény, így az improprius integrál létezik). Ez a definíció megfelelő a függvények egy megfelelően nagy halmazának Lebesgue-integrálásához (az úgynevezett mérhető függvények integrálásához).
Egy tetszőleges f függvény Lebesgue-integrálható, ha az f függvény grafikonja és az x-tengely által bezárt terület véges, vagyis:
Ebben az esetben az integrál, csakúgy, mint a Riemann-integrál esetén az x-tengely fölötti terület és az az alatti terület különbsége:
ahol
Egyéb integrálok[szerkesztés]
Habár a Riemann- és a Lebesgue-integrál a leggyakrabban használt integrálok, számos egyéb definíciója létezik az integrálnak:
- A Darboux-integrál, ami ekvivalens a Riemann-integrállal, vagyis egy függvény, akkor és csak akkor Darboux-integrálható, ha Riemann-integrálható, és az integrálok értéke, már ha létezik, akkor megegyezik. A Darboux-integrál előnye az, hogy könnyebben definiálható a Riemann-integrálnál.
- A Riemann–Stieltjes-integrál, ami a Riemann-integrál egy kiterjesztése.
- A Lebesgue–Stieltjes-integrál, egy Johann Radon által kifejlesztett integrál, ami a Riemann–Stieltjes-integrál és a Lebesgue-integrál általánosítása.
- A Daniell-integrál, amely a Lebesgue-integrál és a Lebesgue–Stieltjes-integrál általánosítása mértékek használata nélkül.
- A Haar-integrál, amit lokálisan kompakt topologikus csoportok fölötti integrálást tesz lehetővé. Alfréd Haar alkotta meg 1933-ban.
Tulajdonságok[szerkesztés]
Linearitás[szerkesztés]
- Egy zárt [a, b] intervallumon Riemann-integrálható függvények halmaza/családja vektorteret alkot, a függvényösszegzés (pontonkénti összegzés) és a skalárral való szorzás műveletével. Ekkor az
- függvény egy lineáris funkcionál ezen a vektortéren. Így, először is az integrálható függvények halmaza/családja zárt az elemek lineáris kombinációjának képzésére, másodsorban pedig, egy lineáris kombináció integrálja megegyezik az őt alkotó elemek integráljának összegével, vagyis:
- Hasonlóan a valós értékű Lebesgue-integrálható függvények halmaza egy adott μ mértékű E mértéktér felett szintén zárt az elemek lineáris kombinációjának való képzésére, vagyis szintén vektorteret alkot és az
- ahol az integrál a Lebesgue-integrál szintén egy lineáris funkcionál, így:
A linearitás és az integrál néhány egyéb tulajdonságai felhasználhatóak arra, hogy egy alternatív definíciót adjunk az integrálnak ezekre építve. A Daniell-integrál pontosan erre épül. Lásd (Hildebrandt 1953) az axiomatikus definícióért.
Integrál-egyenlőtlenségek[szerkesztés]
Számos Riemann-integrálható zárt korlátos [a, b] intervallumon definiált függvényekre igaz egyenlőtlenség ismert, amelyek általánosíthatóak más integrálokra is (például Lebesgue és Daniell integrálokra).
- Alsó és felső korlátok Egy f [a, b] intervallumon integrálható függvény, szükségszerűen korlátos az [a, b] intervallumon. Vagyis eszerint léteznek m és M valós számok úgy, hogy m ≤ f (x) ≤ M, bármely x ∈ [a, b]-re. Mivel így az alsó és a felső közelítő összegek korlátosak m(b − a) és M(b − a) által, így:
- Függvények integráljának egyenlőtlensége Ha f(x) ≤ g(x) minden x ∈ [a, b]-re, akkor f bármely alsó és felső közelítése felülről korlátos a g függvény alsó ill. felső közelítése által. Vagyis:
- Ezt az egyenlőtlenséget tekinthetjük az előző általánosításának is, hiszen M(b − a) egyenlő az konstans M értékű függvény [a, b] intervallum fölötti integráljával.
- Továbbá az is igaz, hogy ha az egyenlőtlenség a függvények között szigorú akkor az integráljuk között is szigorú egyenlőtlenség áll fenn. Vagyis ha f(x) < g(x) minden x ∈ [a, b]-re, akkor:
- Részintegrál Ha [c, d] egy részintervalluma [a, b]-nek és f(x) nemnegatív minden x-re, akkor:
- Függvények abszolút értékének szorzata Ha f és g két függvény akkor ezek szorzatára, hatványaikra és abszolút értékükre igaz, hogy:
- Ha f Riemann-integrálható [a, b]-n, akkor |f| is az, és igaz, hogy:
- Továbbá, ha f és g mindketten Riemann-integrálhatóak, akkor fg szintén Riemann-integrálható és:
- A fenti egyenlőtlenség az integrálokra megfogalmazott Cauchy–Schwarz-egyenlőtlenség, ami fontos szerepet játszik a Hilbert-terek elméletében.
- Hölder-egyenlőtlenség Legyen p és q két valós szám úgy, hogy 1 ≤ p, q ≤ ∞, amikre teljesül még, hogy 1/p + 1/q = 1, és f és g Riemann-integrálható függvények. Ekkor a |f|p és a |g|q függvények szintén Riemann-integrálhatóak és a következő úgynevezett Hölder-egyenlőtlenség teljesül rájuk:
- Ha p = q = 2, a Hölder-egyenlőtlenség megegyezik a Cauchy–Schwarz-egyenlőtlenséggel.
- Minkowski-egyenlőtlenség. Legyen p ≥ 1 egy valós szám és f és g pedig Riemann-integrálható függvények. Ekkor |f|p, |g|p és |f + g|p mind Riemann-integrálhatóak és az úgynevezett minkowski-egyenlőtlenség teljesül:
Megállapodások[szerkesztés]
Ebben a részben f mindig egy valós Riemann-integrálható függvényt jelent. Az
integrálban az integrálási tartomány az [a, b] intervallum, ha a < b. Ha a > b akkor:
- Az integrálási határok felcserélése. Ha a > b, akkor használjuk a következő definíciót:
Így, a = b implikálja, hogy:
- Integrál nulla hosszúságú intervallumon Ha a egy valós szám, akkor
Az utolsó megállapodás azt állítja, hogy egy degenerált intervallum (vagyis egy pont) fölött az integrál értéke nulla. Ha egy függvény integrálható az [a, b] intervallumon akkor ennek bármely részintervallumán is (a degenerált intervallumokon is) integrálható. Ezt felhasználjuk a következő tételben:
- Az integrál additivitása Ha c egy eleme az [a, b] intervallumnak, akkor
A Newton–Leibniz-formula[szerkesztés]
A Newton–Leibniz-formula gyakorlatilag azt mondja ki, hogy a differenciálás és az integrálás egymás ellentétei, vagyis egy folytonos függvényt először integrálva majd deriválva az eredeti függvényt kapjuk. (Ha az integrálás és a deriválás sorrendjét felcseréljük, akkor az eredeti függvényt egy konstans bizonytalansággal kapjuk vissza.) A tétel fontos következménye, hogy a segítségével kiszámíthatjuk határozott integrálok pontos értékét, ha az integrandus antideriváltja ismert.
A tétel állításai[szerkesztés]
Az integrálfüggvény egy primitív függvénye az integrandusnak[szerkesztés]
Legyen f egy folytonos valós [a, b] intervallumon definiált függvény. Ekkor definiáljuk az F függvényt, minden x ∈ [a, b]-re a következőképpen:
Vagyis F integrálfüggvény. Ekkor, F folytonos az [a, b] intervallumon és deriválható az (a, b) nyitott intervallumon és:
minden x ∈ (a, b)-re.
A fenti állítás bizonyítható a Newton–Leibniz-formula hagyományos alakjának (lásd a következő részt) mindkét oldalának az integrál felső határpontja szerinti deriválásával.
Határozott integrál kiszámítása a Newton–Leibniz-tétellel[szerkesztés]
Legyen f egy valós függvény az [a, b] intervallumon, úgy, hogy létezik antideriváltja F az [a, b] intervallumon. Vagyis, f és F olyan függvények, hogy minden x ∈ [a, b]-re igaz, hogy:
Ha f integrálható az [a, b] intervallumon, akkor
Kiterjesztések[szerkesztés]
Improprius integrál[szerkesztés]

integrál egy improprius integrál, amelynek mind az integrálási tartománya, mind az integrandusának értékkészlete nemkorlátos.
A "normális" Riemann-integrál megköveteli, hogy az integrandus értelmezhető legyen az integrálási intervallum minden pontjában és hogy ez az intervallum korlátos legyen. Egy integrált, akkor nevezünk improprius integrálnak ha a fentiek közül egy vagy két kritérium nem teljesül. Ezen integrálokat úgy értelmezhetjük mint a "hagyományos" Riemann-integrálok egy sorozatának határértékét, amely sorozatban az integrál integrálási intervalluma egyre növekszik.
Ha például az integrálási intervallum nemkorlátos, mondjuk a felülről, akkor az integrál a hagyományos Riemann-integrál olyan határértéke, ahol az integrálás felső határa a végtelenbe tart.
Vagyis az improprius integrál olyan hagyományos Riemann-integrálok sorozatának határértéke, ahol az integrálsorozat integráljainak integrálási határai vagy egy meghatározott valós számokhoz vagy (+ vagy −) ∞-hez tartanak. Bonyolultabb esetekben, ha a kritikus pont az integrálási intervallum belső pontja az integrált az adott pontnál két (improprius) részre bontjuk.
Példának vegyük az függvény 0-tól ∞-ig vett integrálját (lásd feljebb a képet). Ahogy x az alsó integrálási határt közelíti a függvény a ∞-be tart, míg az integrálás felső határa szintén ∞, amelybe tartva a függvény értéke 0-ba tart. Vagyis ez bizonyosan improprius integrál lesz. Ha az integrálást, mondjuk 1-től 3-ig végeznénk el akkor a hagyományos Riemann-integrál (vagyis a megfelelő Riemann-összegek határértéke) értéke π/6 lenne. Vegyünk a fenti függvénynek egy integrálját, amelynek alsó határa 1 míg felső határa egy véges t szám (t > 1. Ennek az eredménye . Ennek a kifejezésnek a határértéke létezik, ha t végtelenbe tart, és a határérték π/2. Hasonlóan a függvénynek 1/3-tól 1-ig vett integrálja π/6. Itt a második részben az 1/3-ot lecserélve egy pozitív s számra (úgy, hogy s < 1) kapjuk, hogy ez az integrál . Ennek, ahogy s a 0-hoz tart szintén, létezik határértéke és ez a határérték π/2. Az integrál additivitását felhasználva kapjuk, hogy az improprius integrál
A fenti eljárás ugyanakkor nem mindig végződik sikerrel. A Riemann-integrálok határértéke lehet, hogy nem létezik. Például az 1/x függvény nem integrálható így 0 és 1 között.
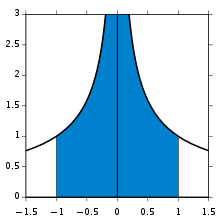
integrandusa ugyan nem korlátos így hagyományosan nem Riemann-integrálható, de mivel mind a "jobb oldali" mind a "bal oldali" integrálrész határértéke létezik így improprius integrállal integrálható.
Ha a "kritikus pont", vagyis az a pont, ahol az integrandus nem korlátos (vagyis olyan pont, amelynek nincs olyan kis sugarú környezete, amelyben a függvény korlátos lenne) egy belső pontja az integrálási tartománynak, akkor az integrál az adott pont mentén felbontandó két improprius integrál összegére.
De a hasonló
integrál nem integrálható ilyen módon mivel sem a "felső" sem az "alsó" részének a határértéke nem létezik.
Többszörös integrál[szerkesztés]

Integrálni nem csak intervallumok felett lehet. Általánosan, egy adott E halmaz fölötti integrált a következőképpen jelölünk:
Itt az x-nek nem muszáj valós változónak lennie, lehet például R3 vektor értékű változó is. A Fubini tétel szerint az ilyen integrálok felírhatóak integrálok integráljaként. Magyarul tehát az ilyen "területek" (vagy "térfogatok", vagy általánosan n-sokaság) feletti integrálok kiszámítható az egyes koordináták szerinti egyenkénti integrálással. (A részletekért és a pontos állításért lásd: Fubini tétel)
Ahogy a pozitív egyváltozós függvények határozott integrálja a függvény és az x-tengely által bezárt területet adja meg, úgy a kettős integrálja egy pozitív kétváltozós függvénynek megadja az integrálási tartomány és a függvény által meghatározott felület által bezárt térfogatot. (Ugyanezt a térfogatot kiszámíthatjuk hármas integrállal is. Ekkor a hármas integrál teljes integrálási tartománya a fent említett tartomány, amit a függvény és a kettős integrál integrálási tartománya bezár — tehát az egész közrezárt térrész, térfogat — míg az integrandus a konstans függvény.) Ha a változók száma és az integrálok száma nagyobb, akkor a kifejezés az adott dimenziós térfogatnak felel meg.
Például, egy téglatest térfogatát — amelynek az oldalai rendre 4, 6, és 5 egység — kétféleképpen is kiszámíthatjuk:
- Egy kettős integrállal:
- az integrandus az f(x, y) = 5 függvény. A D tartomány, amely fölött integrálunk az xy-sík azon része, amely a téglatest alapját adja. Például ha a téglatest (mint hasáb), téglalap alapját a következő egyenlőtlenség adja meg: 3 ≤ x ≤ 7, 4 ≤ y ≤ 10, akkor a konkrét kettős integrál a következő:
- Innen az integrálást elvégezhetjük, bármelyik változóval kezdve. Például ha először az x szerinti integrálást végezzük el (vagyis a belső integrált), akkor az első integrál kiszámítása után, például az különbség meghatározásával vagy akár másképpen, a kapott eredményt a következő "beburkoló" integrál integrandusaként kell kezelni.
- Vagy pedig a
- hármasintegrállal, ahol az integrandus a konstans 1 függvény, míg az integrálási tartomány a teljes téglatest.
Vonalintegrál[szerkesztés]

Az integrálás elve kiterjeszthető általánosabb alaphalmazokra is, mint például adott görbék menti integrálásra vagy felületek feletti integrálásra. Ezen típusú integrálok a fizika fontos eszközei (különféle vektormezőkkel kapcsolatosan).
A vonalintegrál olyan integrál, aminek az integrandusát egy adott görbe mentén integrálunk. Ha az adott görbe zárt görbe, vagyis ha a kezdő és a végpontja megegyezik akkor a vonalintegrál körintegrál.
Vektortér zárt vonalintegrálja (körintegrálja) a makroszkopikus cirkuláció az adott görbe mentén: . Konzervatív erőtér cirkulációja és rotációja is nyilván zérus, míg más erőtereknél ezek általában nem egyeznek meg.[1]
A vontalintegrál integrandusa lehet skalár értékű vagy vektor értékű is. A vonalintegrál értéke az adott görbe mentén előforduló elemek súlyozott összege. (A súlyozást úgy kell érteni, hogy a görbét "lépésekre" bontjuk, vagyis kijelölünk rajta pontokat, amely pontokban vesszük az integrandus értékét és megszorozzuk az előző és az aktuális pont közötti távolsággal. Ha az integrandus nem skalár hanem vektor értékű akkor a görbe adott pontbeli lineáris közelítésével, érintővektorával, való skaláris szorzatát vesszük. Az így kapott szorzatokat összegezzük. Ha minden pont közötti görberésznek a hossza a 0-ba tart akkor kapjuk meg a vonalintegrál pontos értékét.) A fizika számos részén használható az így definiált vonalintegrál. Például egy erőtér egy részecskén végzett munkáját kiszámíthatjuk a vonalintegrál segítségével. A munka alapesetben, ha az erő állandó az elmozdulás pedig egyenes akkor kiszámítható a
képlettel. Ha azonban a részecske egy adott C görbe mentén mozog a térben az adott pontban ráható erőt (amely egy vektor) az F vektormező adja meg akkor az erőtér (a vektormező) által a részecskén végzett munka általánosan megkapható úgy, hogy az utat "infinitezimális" részekre bontjuk amelyeket egyenesnek veszünk. Ekkor a teljes munka megegyezik ezen részutakon végzett munkák összegével, így kapjuk a
vonalintegrált.
Felületi integrál[szerkesztés]

A ''felületi integrál olyan határozott integrál, amelynek integrálási tartománya egy felület. A fentiek szerint (lásd a többes integrálok részt és a Fubini tételt) ez felírható mint egy többszörös integrál. Az integrandus lehet skalár értékű vagy vektor értékű is. Az adott felületet felbonthatjuk kisebb részekre és ezeken a felosztásokon egy Riemann-összeghez hasonló összeget definiálhatunk. A felületi integrál ennek az összegnek a határértéke, ahogy a felosztás minden elemének a mérete/mértéke 0-ba tart.
Például legyen adott egy v vektormező és egy S felület a térben; vagyis, minden x ∈ S-re, v(x) egy vektor. Képzeljük el, hogy egy folyadék keresztülfolyik az S felületen úgy, hogy minden x pontjában az S felületnek a folyadék sebessége v(x). A fluxus azt adja meg, hogy egy adott felületen egységnyi idő alatt mennyi folyadék áramlik át. A fluxus kiszámításához S minden pontjában vennünk kell a folyadék áramlási sebességének és a felület (adott pontbeli) normálisának a skaláris szorzatát. Ez meghatároz egy skalárteret S minden pontjában, amelyet a felületen integrálva kapjuk, hogy:
Az ilyen típusú integrálok jelentik az alapját például az elektrodinamikának.
Kiszámítási módszerek[szerkesztés]
Analitikus[szerkesztés]
A legalapvetőbb módszer egy határozott valós egyváltozós integrál meghatározásához a Newton–Leibniz-tétel használata; Vagyis ha egy adott intervallumon integrálandó függvény, akkor -nek az intervallumon való antideriváltját vagy más néven primitív függvényét (vagyis azt az függvényt, amelynek deriváltja , vagyis ) felhasználva kapjuk, hogy ha az integrálási tartományon sem az integrandusnak (az függvény), sem az integrandus primitív függvényének nincs szingularitása, akkor:
A határozott integrál ugyan nem egyezik meg magával a primitív függvénnyel, (hiszen a határozott integrál egy szám, konkrét érték, míg az primitív függvény egy függvény, egy függvény határozatlan integrálja pedig az összes primitív függvényének a halmaza) de a Newton–Leibniz-formulát felhasználva a primitív függvény használható, határozott integrál kiszámítására.
Ennek a módszernek a legnehezebb lépése a primitív függvény megtalálása. Bizonyos ritka esetekben a primitív függvény ránézésre megállapítható, de a legtöbb esetben különféle módszereket kell alkalmazni az antiderivált meghatározására. A legtöbb ilyen módszer az integrált más (remélhetőlebb egyszerűbben kiszámítható) alakra hozza. A leggyakoribb technikák:
- Helyettesítéses integrálás
- Parciális integrálás
- Inverz függvény szerinti integrálás
- Integrálás trigonometrikus helyettesítéssel
- Tangens félszög helyettesítés
- Integrálás parciális törtekre bontással
- Integrálás redukciós formulákkal
- Integrálás az Euler-képlettel
- Euler-helyettesítés
- Integrál differenciálása
- Integrálás körintegrállal
- Reziduumtétel
A komplexebb integrálok kiszámíthatóak "alternatív" módszerekkel, például egy olyan integrál, amelynek kiszámításához szükséges primitív függvény nem elemi függvény kiszámítható úgy, hogy az integrandust lecseréljük annak Taylor sorával.
Kész formulákért (antideriváltakért lásd: Antideriváltak listája és Riemann-integrálás).
Szimbolikus[szerkesztés]
Bizonyos matematikai illetve fizikai problémáknál esetleg szükség lehet az integrál értékét kifejező explicit formulára. Így megjelentek az integráltáblázatok. Később megjelentek olyan úgynevezett számítógépes algebra rendszerek, amelyek célja hogy bonyolult vagy hosszú, nagy méretű számításokat az emberek helyett elvégezzenek. A szimbolikus integrálási feladatok elsődleges motivációt szolgáltattak ilyen rendszerek fejlesztéséhez.
A szimbolikus integrálás egyik kihívása, hogy akár meglehetősen egyszerű függvények esetén is az antiderivált kiszámítása nagy kihívást jelenthet vagy akár bizonyos esetekben zárt formulaként nem is létezik. Például az exp(x2), xx és a (sin x)/x függvények antideriváltja nem fejezhetőek ki elemi függvényekkel. A Risch-algoritmus (amit például a Mathematica szoftvercsomag is alkalmaz) egy olyan algoritmus, amely egy általános kritériumot ad meg annak eldöntésére, hogy egy adott elemi függvény antideriváltja elemi függvény-e, és ha igen akkor az algoritmussal kiszámítható az adott elemi antiderivált. Azonban a gyakorlat azt mutatja, hogy azok a függvények, amelyek antideriváltja elemi, kisebbségben vannak. Vagyis a számítógépes algebra rendszerek a legtöbb esetben általános elemi integrandus esetén nagy valószínűséggel nem tudnak megoldással szolgálni. Ugyanakkor ha bizonyos nem elemi függvényeket "pluszban elfogadunk elemi függvényeknek", akkor ezeket az előre betáplált, eredetileg nem elemi függvényeket (például Gamma-függvény) felhasználva az algoritmus képes lehet az antiderivált megadására.
Bizonyos integrandusok integrálása olyan gyakran kerül elő, például a fizikában (lásd például: Legendre-függvény), hogy saját nevet kapnak (Gamma-függvény stb). A Risch-algoritmus ilyen nem elemi függvényekkel való kiterjesztése aktív kutatási terület jelenleg is.
Numerikus[szerkesztés]
Mechanikus[szerkesztés]
Egy tetszőleges kétdimenziós alakzat területe meghatározható egy speciális eszközzel az úgynevezett planiméterrel. Egy objektum térfogata megmérhető az általa kiszorított folyadék használatával. Lásd: Arkhimédész.
Néhány fontos határozott integrál[szerkesztés]
Az integrálok segítségével definiált néhány függvény/állandó, például Euler–Mascheroni-állandó:
a Fourier-transzformáció ami a fizika fontos eszköze:
és a Gaussi-integrál, ami a normális eloszlás definiálásának alapja, ill. a valószínűségszámításban használatos:
Fordítás[szerkesztés]
- Ez a szócikk részben vagy egészben az Integral című angol Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.
Jegyzetek[szerkesztés]
Források[szerkesztés]
- Apostol, Tom M. (1967), Calculus, Vol. 1: One-Variable Calculus with an Introduction to Linear Algebra (2nd ed.), Wiley, ISBN 978-0-471-00005-1
- Bourbaki, Nicolas (2004), Integration I, Springer Verlag, ISBN 3-540-41129-1. In particular chapters III and IV.
- Burton, David M. (2005), The History of Mathematics: An Introduction (6th ed.), McGraw-Hill, p. 359, ISBN 978-0-07-305189-5
- Cajori, Florian (1929), A History Of Mathematical Notations Volume II, Open Court Publishing, pp. 247–252, ISBN 978-0-486-67766-8, <http://www.archive.org/details/historyofmathema027671mbp>
- Dahlquist, Germund & Björck, Åke (2008), "Chapter 5: Numerical Integration", Numerical Methods in Scientific Computing, Volume I, Philadelphia: SIAM, <http://www.mai.liu.se/~akbjo/NMbook.html>. Hozzáférés ideje: 2014-07-29 Archiválva 2007. június 15-i dátummal a Wayback Machine-ben
- Folland, Gerald B. (1984), Real Analysis: Modern Techniques and Their Applications (1st ed.), John Wiley & Sons, ISBN 978-0-471-80958-6
- Fourier, Jean Baptiste Joseph (1822), Théorie analytique de la chaleur, Chez Firmin Didot, père et fils, p. §231, <https://books.google.com/books?id=TDQJAAAAIAAJ>
Available in translation as Fourier, Joseph (1878), The analytical theory of heat, Cambridge University Press, pp. 200–201, <http://www.archive.org/details/analyticaltheory00fourrich> - Heath, T. L., ed. (2002), The Works of Archimedes, Dover, ISBN 978-0-486-42084-4, <http://www.archive.org/details/worksofarchimede029517mbp>
(Originally published by Cambridge University Press, 1897, based on J. L. Heiberg's Greek version.) - Hildebrandt, T. H. (1953), "Integration in abstract spaces", Bulletin of the American Mathematical Society 59 (2): 111–139, ISSN 0273-0979, doi:10.1090/S0002-9904-1953-09694-X, <http://projecteuclid.org/euclid.bams/1183517761>
- Kahaner, David; Moler, Cleve & Nash, Stephen (1989), "Chapter 5: Numerical Quadrature", Numerical Methods and Software, Prentice Hall, ISBN 978-0-13-627258-8
- Kallio, Bruce (1966), A History of the Definite Integral, <https://circle.ubc.ca/bitstream/id/132341/UBC_1966_A8%20K3.pdf>. Hozzáférés ideje: 2014-07-29 Archiválva 2014. március 5-i dátummal a Wayback Machine-ben
- Katz, Victor J. (2004), A History of Mathematics, Brief Version, Addison-Wesley, ISBN 978-0-321-16193-2
- Leibniz, Gottfried Wilhelm (1899), Gerhardt, Karl Immanuel, ed., Der Briefwechsel von Gottfried Wilhelm Leibniz mit Mathematikern. Erster Band, Berlin: Mayer & Müller, <http://name.umdl.umich.edu/AAX2762.0001.001>
- Lieb, Elliott & Loss, Michael (2001), Analysis (2 ed.), AMS Chelsea, ISBN 978-0821827833
- Miller, Jeff, Earliest Uses of Symbols of Calculus, <http://jeff560.tripod.com/calculus.html>. Hozzáférés ideje: 2009-11-22
- O’Connor, J. J. & Robertson, E. F. (1996), A history of the calculus, <http://www-history.mcs.st-andrews.ac.uk/HistTopics/The_rise_of_calculus.html>. Hozzáférés ideje: 2007-07-09
- Rudin, Walter (1987), "Chapter 1: Abstract Integration", Real and Complex Analysis (International ed.), McGraw-Hill, ISBN 978-0-07-100276-9
- Saks, Stanisław (1964), Theory of the integral (English translation by L. C. Young. With two additional notes by Stefan Banach. Second revised ed.), New York: Dover, <http://matwbn.icm.edu.pl/kstresc.php?tom=7&wyd=10&jez=>
- Shea, Marilyn (May 2007), Biography of Zu Chongzhi, University of Maine, <http://hua.umf.maine.edu/China/astronomy/tianpage/0014ZuChongzhi9296bw.html>. Hozzáférés ideje: 9 January 2009 Archiválva 2010. június 14-i dátummal a Wayback Machine-ben
- Siegmund-Schultze, Reinhard (2008), "Henri Lebesgue", in Timothy Gowers, June Barrow-Green, Imre Leader, Princeton Companion to Mathematics, Princeton University Press.
- Stoer, Josef & Bulirsch, Roland (2002), "Chapter 3: Topics in Integration", Introduction to Numerical Analysis (3rd ed.), Springer, ISBN 978-0-387-95452-3.
- W3C (2006), Arabic mathematical notation, <http://www.w3.org/TR/arabic-math/>
További információk[szerkesztés]
Online könyvek[szerkesztés]
- Keisler, H. Jerome, Elementary Calculus: An Approach Using Infinitesimals, University of Wisconsin
- Stroyan, K.D., A Brief Introduction to Infinitesimal Calculus, University of Iowa
- Mauch, Sean, Sean's Applied Math Book
- Crowell, Benjamin, Calculus
- Garrett, Paul, Notes on First-Year Calculus
- Hussain, Faraz, Understanding Calculus
- Kowalk, W.P., Integration Theory, University of Oldenburg.
- Sloughter, Dan, Difference Equations to Differential Equations
- Numerical Methods of Integration
- P.S. Wang, Evaluation of Definite Integrals by Symbolic Manipulation (1972)




















































![{\displaystyle \int _{-1}^{1}{\frac {dx}{\sqrt[{3}]{x^{2}}}}=6}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd73b4f0af904c14ed328dffa7434256e9f32eca)
![{\displaystyle {\begin{aligned}\int _{-1}^{1}{\frac {dx}{\sqrt[{3}]{x^{2}}}}&{}=\lim _{s\to 0}\int _{-1}^{-s}{\frac {dx}{\sqrt[{3}]{x^{2}}}}+\lim _{t\to 0}\int _{t}^{1}{\frac {dx}{\sqrt[{3}]{x^{2}}}}\\&{}=\lim _{s\to 0}3(1-{\sqrt[{3}]{s}})+\lim _{t\to 0}3(1-{\sqrt[{3}]{t}})\\&{}=3+3\\&{}=6.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4348fbc3e4bf3a5345fc4c8ca5e93e87307799c)




![{\displaystyle \int _{4}^{10}\left[\int _{3}^{7}\ 5\ dx\right]dy.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98885895d9ae949a16d27d42f3c77b940bea69e7)









![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)







