0,999…
A matematikában a 0,999… végtelen szakaszos tizedestört, amelyet még
- vagy
alakban is írnak. Érdekessége, hogy eggyel egyenlő, minthogy az 1 számnak két tizedestört előállítása is van, az
- 1,000… és a
- 0,999…
Más szavakkal a '0,999…' szimbólum ugyanazt a számot jelöli, mint az '1' szimbólum. Magának az 1 = 0,999… egyenlőségnek (illetve az ilyen típusú egyenlőségeknek) sokféle bizonyítása ismert, ezek a szigorúság különböző fokán állnak, attól függően, hogy középiskolások vagy felsőbb tanulmányokat folytatók számára készültek.
Az utóbbi évtizedekben a matematikapedagógusok vizsgálatokat végeztek arra vonatkozóan, hogy a tanulók mennyire fogadják el az 1 = 0,999… típusú egyenlőségeket. A felmérések szerint a tanulók közül sokan alapvetően megkérdőjelezik vagy elutasítják az egyenlőség fennállását, sokakat pedig a tankönyvek, a tanárok és aritmetikai érvelések meggyőznek arról, hogy igaz a szóban forgó egyenlőség. Mindazonáltal gyakorta ragaszkodnak ahhoz, hogy az állítás igazsága további igazolásra szorul. A diákok érvelése (akár az állítás cáfolásakor, akár igazolásakor) általában a valós számokkal kapcsolatos néhány intuitív elképzelés körül csoportosul. Például, hogy minden egyes számnak egyetlen tizedestört alakja van. Egy másik elképzelés, hogy az 1 a 0,999…-től végtelen kicsiben különbözik, ahol a különbség az infinitezimális egység.
Definíció[szerkesztés]
A 0,999… az a szám, amely a 0; 0,9; 0,99; 0,999, … sorozat határértéke. E sorozat n-edik elemében n–1 kilences van a tizedesvessző után. Így az az állítás, hogy 0,999… = 1, egyenértékű azzal, hogy ez a sorozat az egyhez tart.
A határérték létezik, hiszen a sorozat monoton növekvő (az n+1-edik tag 9·10-n-nel nagyobb az n-ediknél) és felülről korlátos (az 1 jó felső korlát).
A 0,999… = 1 állítás[szerkesztés]
A 0,999… végtelen tizedestört, és az állítás néhány nagyon egyszerű bizonyítása kihasználja a tízes számrendszer aritmetikai tulajdonságait. Az összehasonlítás alaptulajdonsága: két véges tizedestört, aminek különbözőek a jegyeik, különböző számot jelent, eltekintve az utánuk írt nulláktól. Az 1 nem kitüntetett szám abban az értelemben, hogy csak ő rendelkezne két tizedestört alakkal. Minden véges tizedestört alakban írható szám kétféleképpen is megadható. Például:
Továbbá a valós számok végtelen sor alakjában való felírása, mint amely maga a 0,999… kifejezés is, a tízestől különböző számrendszerben sem feltétlenül egyértelmű. Minden számrendszerben vannak olyan valós számok, melyek többféleképpen írhatók fel az adott számrendszerben, mi több, ez még a tört és irracionális alapú számrendszerekben is így van. A jelenség alkalmazásaként megemlíthetjük a Cantor-halmazra vonatkozó vizsgálatokat. Speciálisan, bármely 0,99…9 alakú szám egynél kisebb, ha véges sok kilences van benne.
Kételkedők és érveik[szerkesztés]
Még a matematika szakos hallgatók is gyakran kételkednek 0,999… és 1 egyenlőségében. Az okok között szerepel a határérték szabatos fogalmától való makacs idegenkedésük és az infinitezimális mennyiségek természetéről való – a bevett nézethez képest – másként gondolkodásuk. A zavart több közös tényező fokozza:
- Úgy látják, hogy minden valós számnak egyféle tizedestört alakja van. Számukra az a jelenség, hogy egy számnak két lényegesen eltérő tizedestört alakja van, paradoxnak tűnik, zavarukat csak fokozza, hogy pont az 1-ről van szó, amiről azt gondolják, hogy ennek természetét már jól ismerik.[1]
- Néhányan úgy értelmezik a "0,999…" alakot, mint ami sok, de véges sok 9-esből áll, melyek darabszáma esetleg változó vagy határozatlanul nagy. Ha pedig mégis elfogadják a végtelen sok 9-est, akkor pedig egy utolsó 9-est képzelnek valahová a végtelenbe.[2]
- A határérték fogalmának intuitív vagy homályos bevezetése, feltételezése az oktatásban ahhoz vezethet, hogy a hallgatók a határérték megadását inkább valamiféle végtelen eljárásnak fogják fel, mint egy konkrét értékre való rámutatásnak, előtérbe helyezve azt a jelenséget, hogy a sorozatnak nem kell elérnie határértékét. Amikor a sorozat és határértékének különböző volta a hallgatók számára világos, akkor intuitív tárgyalás esetén számukra a "0,999…" szimbólum sokkal inkább sorozat, mint határérték.[3]
- Egyesek a 0,999…-et rögzített értéknek fogják fel, ami egy infinitezimális mértékű mennyiséggel kisebb 1-nél.
- Mások meggyőződése, hogy egy konvergens sor összege legjobb esetben is csak közelítés, azaz 0,999… ≈ 1.
Mindezen szemléletek a valós számok hagyományos értelmezésében hibás gondolatmenetek alapjai, ám néhány közülük érvényes lehet más számkörökben, például a nemsztenderd valós számok elméletében. Hasznosak lehetnek továbbá akár általános matematikai értelemben, akár tanulságos ellenpéldaként tekintve, ami a 0,999… jobb megértéséhez vezethet.
Nagy részükkel David Tall is találkozott, amikor a tanulást és a gondolkodást tanulmányozta hallgatói körében. Úgy találta, hogy a hallgatók azért utasították el először ennek az egyenlőségnek a gondolatát, mert a 0,999… számot egy olyan sorozatnak látták, amely egyre inkább megközelíti az 1-et, és nem egy rögzített értékként.
A következő vélemények is felmerültek:
- A 0,999… szám a legnagyobb végtelen tizedestört, ami kisebb 1-nél.
- Nem határozhatod meg, hogy hány tizedesjegye van.[4]
Legtöbbjük meggyőzhető az elemi bizonyítások segítségével, de vannak, akik továbbra is kételkednek és frusztrálódnak.[5] A hallgatók, akik képesek precíz definíciókat alkalmazni, egy meglepő eredmény láttán automatikusan újra az intuitív képek hatása alá kerülnek, így a kevésbé elemi bizonyításokat sem mindig értik meg.
Egy valós analízist tanuló hallgató például képes volt belátni, hogy 1⁄3 = 0,333… a szuprémum segítségével, de még mindig ellenállt a 0,999… = 1 egyenlőségnek, a hosszú osztásra vonatkozó tapasztalataira hagyatkozva.[6] Mások, akik szintén be tudják bizonyítani, hogy 1⁄3 = 0,333…, még mindig nem érzik megfelelőnek a törteket használó bizonyítást, mondván, hogy a logika fontosabb a matematikában, mint a számítások.
Joseph Mazur mesélte, hogy volt egy egyébként kitűnő hallgatója, aki majdnem mindenben kételkedett, amit az oktatója mondott, de mindig hitt a számológépének. Azt hitte, hogy 9 tizedesjegy elég a matematikához, még ahhoz is, hogy kiszámolja 23 négyzetgyökét. Képtelen volt megérteni a 9,99… = 10 határértékes bizonyítását, és „vadul elképzelt végtelen növekvő sorozatnak” nevezte.[7]
Ed Dubinsky és Tsai elmélete szerint, akik a 0,999… számot véges, de meghatározatlanul hosszúnak fogják fel, amely egy végtelenül kis mennyiséggel kisebb 1-nél, azok nem értették meg a végtelen tizedestörteket eredményező végtelen sorokat. Megint mások a sor és sorösszeg fogalmát nem képesek megkülönböztetni. Számukra a 0,999… egy sort (tehát egy számítási eljárást és nem sorösszeget, vagyis számot) jelöl, míg az 1 az szám, azaz nem ugyanolyan minőségű, így nem lehetnek egyenlők.[8]
Bizonyítás[szerkesztés]
Egyszerű bizonyítás[szerkesztés]
Ha , akkor . Mivel , ezért
Algebrai bizonyítások[szerkesztés]
Bizonyítás törtekkel[szerkesztés]
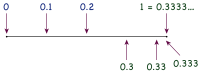
A törtek felírhatók véges vagy végtelen szakaszos tizedestört alakban. Így például 1⁄3 egyenlő lesz a 0,333… végtelen szakaszos tizedestörttel, amiben a 3-as számjegy végtelen sokszor ismétlődik. Ezt az egyenlőséget hárommal szorozva adódik a 0,999… = 1 egyenlőség.
Minden 3-as számjegy 3-mal szorzódik, így lesz belőle 9, ezért 3 × 0,333… = 0,999… (nincs átvitel), és 3 × 1⁄3 = 1, tehát .[9]
A bizonyítás egy másik változata az 1/9 = 0,111… egyenletet szorozza 9-cel.
|
|
|
Ugyanennek a bizonyításnak egy könnyített változata 9/9 = 1, és 9/9 = 0,999…, mivel 1/9 = 0,111… Az egyenlőség tranzitivitása miatt 1 = 0,999…
Ez az okoskodás hallgatólagosan feltételezi, hogy a végtelen tizedes törtekkel ugyanúgy kell szorozni, mint a végesekkel: itt például bizonyítás nélkül elfogadjuk, hogy a
típusú azonosságokból következik, hogy
Számjegy-manipuláció[szerkesztés]
A bizonyítás egy másik módja azt a tényt használja ki, hogy 10-zel szorozva a jegyek nem változnak, csak a tizedesvessző mozdul el, és hallgatólagosan feltételezi, hogy ez a szabály a végtelen tizedes törtekre is érvényes. Ezért 10 × 0,999… = 9,999…, ami 9-cel nagyobb az eredeti számnál.
A 9,999… – 0,999… kivonás jegyről jegyre végezhető el, és 9 – 9 = 0 minden, a tizedesvessző utáni jegyre fennáll. Így a művelet eredménye 9.
Most felírunk egy egyenletrendszert, és megoldjuk 0,999…-re. Nevezzük ezt a számot c-nek. Az egyenlet így néz ki: 10c – c = 9. Ez lényegében ugyanaz, mint 9c = 9. Ezt 9-cel osztva c = 1.[9]
Egyenletek sorozatával felírva
Valós analízis[szerkesztés]
A 0,999…-re vonatkozó kérdés valójában nem érinti az analízis megalapozási problémáit, valós számok bevezetéséhez nincs szükség tizedestört-előállításra, így az ezzel a kérdéssel való foglalkozás a matematika szokásos felépítésében sokáig halogatható. Előbb-utóbb azonban elkerülhetetlen, hogy az analízis definiálja a valós számok tizedestört alakját. Ezen olyan
szimbólumsorozatot értünk, melyben b0 jelöli a szám egészrészét, a törtrészt pedig a
végtelen, tizedesjegyekből álló sorozat elemei reprezentálják. A tizedesvessző az egész- és a törtrészt választja el. A 0,999… vizsgálatánál eltekinthetünk a negatív egészrész esetétől, sőt akár magától az egészrésztől is. Világos, hogy:
- a törtrészben végtelen sok jegy is lehet,
- a jelölés helyiértékes, azaz például az 5 az 500-ban tízszer annyit ér, mint az 50-ben, és 0,05-ben tízszer annyit ér, mint 0,005-ben.
Végtelen sorozatok és sorok[szerkesztés]
A végtelen tizedestörteket többnyire végtelen sorok összegeként vezetik be. Általános esetben a tizedestört alak által kijelölt szám értéke:
Mivel a 0,999…-ben a tizedesjegyek mind azonosak, ezért az előbbi képlet kiszámításához elegendő a mértani sorokról szóló tételhez fordulnunk. Eszerint, ha a tetszőleges valós szám, amely a mértani sor kezdőeleme és |r| < 1 szám, akkor
Jelen esetben a sor az előbbi második tagjánál kezdődik:
A 0,999… esetén a = 9 és r = , ezért a képlet ekkor
Ez a bizonyítás (pontosabban a 9,999… = 10 bizonyítása) Leonhard Euler 1770-es Az algebra elemei című munkájában is szerepel.[11]
Felhasználtuk azt a tételt, ami szerint, ha (an) konvergens számsorozat, és határértéke a, akkor tetszőleges -re a can sorozat is konvergens, és határértéke ca.
Ennek bizonyításához először tekintsük azt a speciális esetet, amikor a = 0.
Legyen ε tetszőleges pozitív szám, és K > |c| pozitív szám. (an) tart a nullához, ezért ε /K -hoz van egy elég nagy N szám, hogy ha n>N, akkor |an| < ε /K. Eszerint minden n>N-re |(ca)n| = |can| < Kε /K=ε, és ezzel can szintén a nullához tart.
Ha a nem nulla, akkor a sorozat minden tagjából levonunk a-t, így olyan (an – a) sorozatot kapunk, amelynek határértéke nulla. A speciális eset szerint, ha c-vel szorozzuk, akkor is tart a nullához, ezért c(an – a) = (can – ca) határértéke nulla, tehát a can sorozat ca-hoz tart.[12]
Hasonlók tudhatók két sorozat összeadásáról és kivonásáról is. Itt mindkét sorozatban elmegyünk addig, amíg ε / 2 -nél közelebb kerülünk a határértékhez. Megnézzük, melyikben nagyobb a küszöbszám. Ez a küszöb jó lesz az összegsorozathoz és az ε számhoz.
Ezzel a tétellel bizonyítható a számjegy-manipuláció és a törtekkel való bizonyítás helyessége is.
A mértani sor összegére vonatkozó eredmény Eulernél sokkal korábbi. Már Apollóniosz is használta a parabolaszelet területének meghatározására. A 18. században a deriválásokat tipikus módon a sorokkal végzett tagonkénti műveletekkel végezték úgy, ahogy ennek a szócikknek az algebrai megoldásokat részletező szakaszában bemutattuk. Bonnycastle 1811-es An Introduction to Algebra című tankönyvében már felvonultatja a 0,999…-ra vonatkozó állítás mértani sorral történő bizonyítását.[13] A 19. században pontosították a sorösszeg fogalmát, oly módon, ahogy az ma szokásos: a sor összege nem más, mint egy sorozat részletösszegei sorozatának határértéke. A határérték szigorú fogalmára hivatkozó bizonyítás szerepel például Rudin könyvében.
Bővebben. A (x1, x2, x3, …) sorozat határértéke az x szám, ha az |xn – x| távolság tetszőlegesen kicsivé válik, amint az n elegendően nagy. A 0,999… = 1 kijelentés megfogalmazható a határérték felhasználásával és igazolható is:
Az utolsó lépésnél – hogy lim 1/10n = 0 – gyakran hivatkoznak a valós számok arkhimédészi tulajdonságára, azaz arra, hogy minden valós számnál van nagyobb természetes szám (amiből következik, hogy 1/n minden pozitív valós számnál kisebbé válik, ahogy az 1/10n is).
Egymásba skatulyázott intervallumok és legkisebb felső korlátok[szerkesztés]

A sorösszeggel történő definíció lehetőséget nyújt arra, hogy definiáljuk azt a valós számot, melyet a tizedestört-előállítás meghatároz. Ezzel ellenkező szemlélet, hogy egy adott valós számhoz definiálunk egy olyan tizedestört alakot, amely megnevezi.
Tegyük fel, hogy az x valós számról azt tudjuk, hogy a [0; 10] intervallumba esik. Felírjuk egy tizedes előállítását.
- A [0; 10] intervallumot feloszthatjuk 10 részre úgy, hogy a végpontok fedjék egymást. Az x szám tehát az
zárt intervallumok egyikébe biztosan beleesik. Tegyük fel, tudjuk, hogy a [2; 3]-ban van. Ekkor rögzítsük a b0 = 2 számot, mint tizedestört alakban az egész számot.
- A [2; 3] intervallumot osszuk tovább: [2; 2,1], [2,1; 2,2], …, [2,8; 2,9], [2,9; 3]. Ekkor x ezek valamelyikébe esik, mondjuk a [2,8; 2,9]-be. Rögzítsük a b1 = 8-as számjegyet, mint az első számjegyet.
- Az eljárást folytatva egymásba skatulyázott intervallumok végtelen sorozatát kapjuk, amelyeket a jegyek végtelen sorozata címkéz: b0, b1, b2, b3, …, ami így írható:
- x = b0,b1b2b3…
Ezt az eljárást szem előtt tartva, az, hogy 1 egyaránt lehet 1,000… és 0,999…, annak a következménye, hogy az 1 szám eleme mind a [0;1], mind az [1;2] intervallumnak, így az eljárás első lépésében akármelyiket választhatjuk az 1 tizedestört előállítására. Az eljárás helyességéhez azt kell megmutatnunk, hogy a tizedestört-előállítás egyetlen valós számra mutat. Ezt meg lehet oldani határértékkel, de más konstrukciók a rendezést használják.[15]
Nyílegyenes választás a beágyazott intervallumok tétele, amely kimondja, hogy egymásba ágyazott zárt intervallumok végtelen sorozatának egy közös pontja van. Így b0,b1b2b3… az a szám, amely benne van a {b0, b0.b1, b0.b1b2, …} intervallumok mindegyikében.
Ez a tétel a valós számok egy még alapvetőbb tulajdonságán nyugszik: a legkisebb felső korlátok, azaz a szuprémumok létén. Ehhez definiálni kell b0-t a b1b2b3… approximáló sorozat legkisebb felső korlátjaként. Látható, hogy ez az eljárás konzisztens a felosztási folyamattal, amiből ismét következik, hogy 0,999… = 1.
Az, hogy egy valós számnak két különböző tizedestört alakja lehet, csupán annak a következménye, hogy van két, valós számokból álló halmaz, amelynek ugyanaz a legkisebb felső korlátja.[16]
Valós számok[szerkesztés]
Más megközelítések a valós számokat a racionális számok fölötti struktúraként tekintik. Az axiomatikus halmazelmélet szerint a 0-val kezdődő természetes számok mindegyikének van rákövetkezője. Az így definiált természetes számok ellentettjeikkel együtt kiadják az egész számokat, és ezek hányadosai pedig a racionális számokat. Ezeken a számkörökön belül aritmetikai műveletek is végezhetők: ezek a számok összeadhatók, kivonhatók, szorozhatók, oszthatók egymással. Sőt, rendezett struktúrákat adnak, így az egyik szám összehasonlítható egy másikkal, és nemcsak azt lehet megkérdezni, hogy egyenlőek-e, hanem lehet az egyik kisebb vagy nagyobb a másiknál.
Az előzőknél jóval nagyobb kiterjesztés a racionális számokról a valósakra áttérni. Többféle lehetőség is kínálkozik erre, ezek közül kettőt 1872-ben publikáltak: a Dedekind-szeleteket és a Cauchy-sorozatokat. A valós analízisről szóló jegyzetek nem tartalmazzák a 0,999… = 1 direkt bizonyítását, inkább az analízis axiómáival foglalkoznak. A legtöbb konstrukciónak az a célja, hogy bemutassa vagy igazolja a valós számok axiómáit, amelyek a fenti bizonyításokat támogatják. Néhány szerzőnek viszont az az ötlete, hogy elsőre a konstrukciókat mutassák be, mert úgy logikusabb a felépítés, és a végeredmények függetlenebbek.[17]
Dedekind-szeletek[szerkesztés]
A Dedekind-szeleteket használó megközelítés szerint minden valós szám a nála kisebb racionális számok halmaza.[18] Speciálisan, az 1 azoknak a racionális számoknak a halmaza, amelyek kisebbek 1-nél.[19] Minden pozitív tizedestört meghatároz egy Dedekind-szeletet: azoknak a véges tizedestörteknek a halmazát, amelyek levágással kaphatók belőle. Így a 0,999… valós szám tekinthető az olyan r valós számok halmazának, amelyekre r < 0 vagy r < 0,9 vagy r < 0,99 vagy r kisebb, mint egy alakú szám. 0,999… összes eleme kisebb, mint 1,[20] így eleme az 1 valós számnak. Visszafelé, az 1 elemeire , amiből . Mivel 0,999… és 1 ugyanazokat az elemeket tartalmazza, ezért a két halmaz, így a két szám egyenlő.
Cauchy-sorozatok[szerkesztés]
A valós számok konstrukciójának egy másik módja a Cauchy-sorozatokat használja.
Először is x és y távolságát az |x ‒ y| értékkel definiálja, ahol |z| a szokott értelemben vett abszolútérték-függvény. A továbbiakban a megközelítés ezt a távolságmértéket használja.[21]
A sorozatokat leképezésként értelmezi a pozitív egészek halmazáról a valós számok halmazába, ahol is n-nek a sorozat n-edik eleme felel meg. A valós számokat Cauchy-sorozatokként definiálja, ahol is két sorozatot egyenlőnek tekint, ha az (xn ‒ yn) sorozat határértéke 0.
Ebben a megközelítésben azt kell bizonyítani, hogy az
- 1 – 0, 1 – (9 / 10), 1 – (99 / 100), … = 1, (1 / 10), (1 /100), …
sorozat határértéke 0. A sorozat n-edik tagját tekintve elég megmutatni, hogy: Ez pedig nyilvánvaló, hiszen a 0,1 < 1 hányadosú mértani sor határértéke véges.
A Cauchy-sorozatokat használó definíciót elsőként Eduard Heine és Georg Cantor publikálta, mindketten 1872-ben.[22]
Általánosítások[szerkesztés]
A 0,999… = 1 állítás és bizonyításai többféleképpen is általánosíthatók.
- A nem nulla véges tizedestörtként felírható számoknak van egy másik alakjuk is, amely végtelen sok 9-cel végződik. Például 0,24999… = 0,25 a speciális esethez hasonlóan. Az ilyen számok halmaza sűrű.[23]
- Másrészt a tízes számrendszerbeli esethez hasonlóan minden számrendszerben felvetődik ugyanez a kérdés. Kettes számrendszerben 0,111… = 1, és hármas számrendszerben 0,222… = 1. A valós analízisről szóló könyvek rögtön ezzel az általánosítással foglalkoznak, és a kettes és a hármas számrendszerből hoznak példákat.[24]
Az 1 alternatív reprezentációja a nem egész alapú számrendszerekben is megjelenik. Például abban a számrendszerben, amelynek , az aranymetszési arány az alapja, az 1 két lehetséges reprezentációja 1,000… és 0,101010…; de végtelen sok olyan reprezentáció is van, amelyben szomszédos 1-esek is vannak. Sőt, majdnem minden 1 és 2 közötti számra 1-nek megszámlálhatatlanul sok kifejtése van. Másrészt megszámlálhatatlanul sok olyan alap van, amire az 1-nek csak egy másik kifejtése van az adott alapra nézve. Ezt az eredményt elsőként magyar matematikusok látták be, mégpedig Erdős Pál, Horváth Miklós és Joó István 1990 körül. 1998-ban Komornik Miklós és Paola Loreti meghatározta a legkisebb ilyen bázist, 1,787231650…-t; ahol is fennáll 1 = 0,11010011001011010010110011010011…; a jegyeket a Thue–Morse-sorozat adja, ez a felírás pedig nem periodikus.[25]
Egy még messzebb menő általánosítás a még általánosabb helyi értékes számrendszerekről szól. Ezekben is többféle reprezentáció létezik, és a nehézségek is ezzel együtt nőnek.
A kiegyensúlyozott hármas számrendszerben (ahol a jegyek 0, +1, -1), 1/2 = 0,111… = 1,111….
A faktoriális számrendszerben 1 = 1,000… = 0,1234….
Marko Petkovšek belátta, hogy a helyi értékes rendszerek használatának szükséges következménye a többféle számábrázolás. Minden, az összes valós számot ábrázoló számrendszerben sűrű azoknak a valós számoknak a halmaza, amelyek többféleképpen is reprezentálhatók.[26]
Alkalmazásai[szerkesztés]
Az egyik alkalmazás az elemi számelmélethez tartozik. 1802-ben H. Goodwin publikálta megfigyelését a végtelen szakaszos tizedestörtekről. Ha a tört nevezője a prímszámok egy bizonyos részéhez tartozik, akkor efféle dolgok történnek:
- 1/7 = 0,142857142857… és 142 + 857 = 999.
- 1/73 = 0,0136986301369863… és 0136 + 9863 = 9999.
E. Midy egy ennél általánosabb tételt, Midy tételét bizonyította be 1836-ban. A publikáció homályos volt, és tisztázatlan, hogy használta-e a 0,999…-ről szóló eredményt, de W. G. Leavitt egy modern bizonyítása igen. Ha bizonyítható, hogy a 0,b1b2b3… végtelen tizedestört egész szám, akkor ennek a 0,999…-nek kell lennie, ami a tételben szereplő 9-esek forrása.[27]

Az ez irányú próbálkozások motiválhatják a legnagyobb közös osztó, a moduláris aritmetika, a Fermat-prímek, a rendezés, a csoport és a kvadratikus reciprocitás fogalmának megértését.[28]
Visszatérve a valós analízisre, a 3-as számrendszerbeli analóg 0,222… = 1 kulcsszerepet játszik a legegyszerűbb fraktálok egyikében, a Cantor-halmazban:
- Az egységintervallumba eső szám akkor és csak akkor eleme a Cantor-halmaznak, ha felírható a hármas rendszerben csak a 0 és a 2 jegyek használatával.
A felírás n-edik jegye a pont helyére utal a konstrukció n-edik lépésében. Például a ²⁄3 a megszokott 0,2 vagy 0,2000… alakjában van adva, mert az első törléstől jobbra és az összes törléstől balra fekszik. Az 1⁄3 nem 0,1-ként, hanem 0,0222… -ként van reprezentálva, mert az első törléstől balra és az összes törléstől jobbra fekszik.[29]
A kilencesek Cantor más munkáiban is visszatérnek. Az egységintervallum pontjainak megszámlálhatatlanságát a Cantor-féle átlós eljárással is bizonyítani lehet. A bizonyításnak el kell kerülnie az olyan párokat, mint amilyen 0,2 és 0,1999… . Egy egyszerű módszer minden számot végtelen tizedestört alakba ír, tehát a véges tizedestörtekkét felírható számokat is így adja meg. Egy másik módszer kikerüli a végtelen szakaszos kilenceseket.[30] Cantor eredeti érvelése a kettes számrendszert használja, és a hármas számrendszerbeli felírásokat 2-es számrendszerbe transzformálva a Cantor-halmaz megszámlálhatatlan volta bizonyítható.[31]
Az állítás más számkörökben[szerkesztés]
Ámbár a valós számok egy nagyon hasznos számkör, a 0,999… valós számnak tekintése konvenció. Timothy Gowers érvelése szerint a 0,999… = 1 egyenlőség konvenció:
Ez azonban nem egy önkényes megállapodás, hiszen elvetése vagy a megszokott aritmetikai szabályok elvetését, vagy furcsa új objektumok bevezetését kívánja meg.[32]
Definiálhatók új számkörök, melyek más szabályokat használnak, vagy új objektumokat vezetnek be. Ezekben a számkörökben nem mindig működnek a valós számoknál alkalmazott bizonyítások, így újra kell vizsgálni a 0,999… = 1 kérdését, és egyes ilyen számrendszerekben ez az egyenlőség nem teljesül. Mások viszont inkább a valós számok kiterjesztései, mint független alternatívák, és így a 0,999… = 1 egyenlőség továbbra is fennáll.
Infinitezimálisok[szerkesztés]
A 0,999… = 1 egyes bizonyításai kihasználják, hogy a standard valós számok arkhimédészien rendezettek: nincsenek nemnulla infinitezimálisok. De vannak nem arkhimédészi rendezett algebrai struktúrák, a valós számok egyes alternatíváit is beleértve. A 0,999… jelentése attól függ, hogy melyik struktúrában tekintjük.
Például a duális számok magukban foglalnak egy infinitezimális elemet, amit ε jelöl. Ez megfelel a komplex testbővítés képzetes egységének, kivéve, hogy ε² = 0. A duális számokon megadható egy lexikografikus rendezés, amiben ε többszörösei nem arkhimédészi elemek lesznek.[33] Jegyezzük meg, hogy a duális számok körében továbbra is teljesül 0,999… = 1, mivel a duális számok a valós számok kiterjesztései. A duális számok között nincs legkisebb pozitív szám, mert ha van ε, akkor van ε/2 is.
A standard valós számoknak léteznek más alternatíváik is. Ezek konstruálhatók a toposzelmélet segítségével és a többértékű logikával, vagy speciális esetben a klasszikus logikával. Például vannak olyan konstrukciók, amelyekben az infinitezimális elemeknek nincs reciprokuk.[34]
A nem standard analízis arról ismert, hogy egy olyan számkörrel működik, ami infinitezimálisok teljes tömbjeit tartalmazza. Ez lehetőséget ad az analízis egy másfajta megközelítésére, ami talán intuitívabb, mint a standard változat.[35]
A. H. Lightstone 1972-ben foglalkozott a nem standard decimális kifejtésekkel, ahol a (0, 1) kiterjesztett valós számoknak egyértelmű a kiterjesztett decimális kifejtése. A 0,ddd…;…ddd… alakú jegysorozatokat kiterjesztett egész számokkal indexelte. Ebben a formalizmusban a 0,333… -nak két természetes kiterjesztése van:
- 0,333…;…000… nem létezik
- 0,333…;…333… = 1/3, mégpedig egész pontosan.[36]
A kombinatorikus számelmélet alternatív valós számokat ad meg, a végtelen kék-piros Hackenbush-stringeket részletes releváns példaként. 1974-ben Elwyn Berlekamp megfeleltette egymásnak a Hackenbush-stringeket és a valós számok kettes számrendszerbeli leírását az adattömörítés által motiválva. Például a LRRLRLRL… Hackenbush-string értéke 0,010101… = 1/3.
Az LRLLL… string, amely 0,111…-t jelent, infinitezimálisan kisebb egynél, a különbségük a szürreális 1/ω szám, ahol ω a legkisebb végtelen rendszám. A releváns játszma LRRRR… vagy másként 0,000….[37]
A kivonás eltörlése[szerkesztés]
A bizonyítás egy másik megkérdőjelezhető pontja az 1 ‒ 0,999… kivonás. Ha ez a kivonás nem végezhető el, akkor 0,999… < 1. Léteznek olyan struktúrák is, amelyekben működik az összeadás, de a kivonás nincs értelmezve: ilyenek például a kommutatív félcsoportok, a kommutatív monoidok és a félgyűrűk. Richman két ilyen rendszert tekintett, és belátta, hogy 0,999… < 1.
Először is Richman a nem negatív tizedes számokat végtelen tizedestörtekként definiálta. Megadott egy lexikografikus rendezést és egy összeadási műveletet. Ebben a rendszerben 0,999… < 1, mivel 0 < 1 az első helyen, de minden végtelen x-re, amire 0,999… + x = 1 + x. Így a tizedes számok körében az összeadás nem mindig megfordítható, és nincs köztük az 1⁄3 szám sem. A szorzás bevezetésével a tizedes számok pozitív, teljesen rendezett, kommutatív félgyűrűt alkotnak.[38]
A szorzás definiálásához Richman egy másik rendszert is bevezetett, amit D-szeletnek nevezett. Ez a tizedestörtek Dedekind-szeleteinek halmaza. Rendszerint ez a definíció a valós számokhoz vezet, de a d tizedestört két szeletet is megenged: (‒∞, d ) és (‒∞, d ], ez utóbbi a principális szelet. Ennek eredményeként a valós számok nehezen élnek együtt a tizedestörtekkel. Újra 0,999… < 1.
Nincsenek pozitív infinitezimálisok a D-szeletekben, de itt rengeteg negatív infinitezimális jelenik meg, például 0‒, amelynek nincs végtelen tizedestört alakja. Richman arra a következtetésre jutott, hogy 0,999… = 1 + 0‒, ahol a „0,999… + x = 1” egyenletnek nincs megoldása a tizedes számok körében.[39]
p-adikus számok[szerkesztés]
Amikor szóba kerül a 0,999…, akkor sokan azt hiszik, hogy van egy utolsó kilences a végtelenben. Az 1 ‒ 0,999… kivonás eredménye a 0,000…1 pozitív szám, ahol az 1 a végtelenben van. Az intuíció világos: ha a 0,999… utolsó kilenceséhez hozzáadunk egyet, az végigfut, lenulláz minden kilencest és az első helyen 1-et ad. Az ötlet egyebek között azon bukik meg, hogy nincs utolsó kilences a 0,999… számban.[40]
Máshol kell keresni a kilencesek egy olyan végtelen sorát, amiben van egy utolsó kilences.
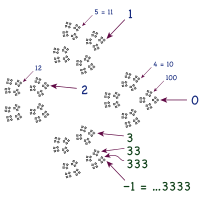
A p-adikus számok egy alternatív számrendszer, amellyel a számelmélet foglalkozik. Miként a valós számok, úgy a p-adikus számok is felépíthetők racionális számok Cauchy-sorozataként. Felfoghatók valós számokként, egy másik metrikában, egy másik helyi értékes rendszerrel. A konstrukció egy nem arkhimédészi metrikát használ, amiben 0 közelebb van p-hez, mint az 1, és pn közelebb van a nullához, mint p. A p-adikus számok testet alkotnak, ha p prím, és gyűrűt, ha összetett, mint amilyen a 10 is. Így a p-adikus számok körében műveletek végezhetők, és ehhez nem kellenek infinitezimálisok.
A 10-adikus számok körében a decimális kifejtések analógja balra folyik. A …999 10-adikus kifejtésben van utolsó kilences, de nincs első. Ha hozzáadunk egyet, akkor ez történik: 1 + …999 = …000 = 0, és így …999 = ‒1.[41]
Egy másik bizonyítás mértani sorokat használ. A …999 által implikált végtelen sor nem konvergál a szokásos valós metrikában, de a p-adikus metrikában igen. Így használható a formula:
A harmadik módszert egy hetedikes találta ki, aki kételkedett tanárának határértékes bizonyításában, hogy (a valós számokon) 0,999… = 1, de a tízzel szorzásos bizonyítás arra inspirálta, hogy ugyanezt a másik irányba is elvégezze (a 10-adikus számok körében): ha x = …999, akkor 10x = …990, így 10x = x – 9, tehát x = –1.[41]
Utolsó kiterjesztésként felvetődik még, hogy ha 0,999… = 1, és …999 = –1, akkor …999,999… egyenlő-e nullával. Ennek az egyenlőségnek nincs értelme sem a valós számok, sem a p-adikus számok körében, de kiderül, hogy van értelme, és igaz is, ha bevezetjük a dupla tizedestörteket a valós számok reprezentálására, ahol mind a tizedesvessző előtt, mind azután végtelen sok jegy állhat.[43]
Kapcsolódó problémák[szerkesztés]
- Zénón paradoxona a futóról egy hasonló paradoxon. A futó paradoxona matematikailag modellezhető, és ugyanúgy, mint a 0,999… = 1, a mértani sorok segítségével feloldható. Nincs tisztázva, hogy ez a matematikai felfogás megfelel-e a Zénón által kutatott metafizikai fogalmaknak.
- A matematikai folklórban elterjedt csokipapíros történet:[44]
Volt egy csokoládé, amibe reklámcéllal szelvényt is csomagoltak. Tíz ilyen szelvényért egy újabb tábla csokoládét lehetett kapni. Kérdés: hány tábla csokoládét ér egy ilyen tábla csokoládé, teljes csomagolásban?
A csomagolásban van egy tábla csokoládé, és egy szelvény is, amiből tízért lehet egy csokoládét kapni. Tehát ez egy tized csokoládé, a hozzá járó tized szelvénnyel. Ezzel a gondolatmenettel a teljes csomagolásban levő csokoládé értéke
Másrészt a teljes csomagolásban levő csokoládé értéke egész pontosan :
A csomagolásban van egy csokoládé, ez 1. Elég azt igazolni, hogy egy szelvény 1/9 csokoládét ér. Kilenc szelvényhez kérve egy csokit, és utólag a tíz (9+1) szelvénnyel fizetve ez is belátható: szelvény nem maradt, és a csoki is ki lett fizetve.[45]
- A nullával való osztás is előfordul a 0,999… -ről szóló népszerű vitákban, és szintén nagy figyelmet kap. Majdnem minden modern felépítés definiálatlanul hagyja a nullával való osztást, míg a legtöbb szerző definiálja 0,999… -et. Néhány más rendszer viszont definiálja, mint például a komplex analízis, ahol a végtelennel kibővített komplex síkon ennek semmi akadálya sincs; 1/0 tehát definiálható végtelennek.[46] Valóban, az eredmények mélyek, és sok mérnöki és fizikai problémára alkalmazhatók. Néhány kiemelkedő matematikus amellett érvelt, hogy először egy ilyen definíciót kell bevezetni, és csak aztán kell a számköröket tárgyalni.[47]
- A negatív nulla egy másik redundáns jelenség a számírással kapcsolatban. Az olyan számkörökben, mint például a valós számok, ahol 0 az additív semleges elem, a ‒0" szokásos értelmezése a 0 additív inverze, amiből következik, hogy ‒0 = 0.[48] Néhány tudományos alkalmazás azonban külön pozitív és negatív nullát használ, ahogy a legtöbb elterjedt számítógépes számírási rendszer. Például az egész számok tárolása előjellel és nagyságrenddel, vagy az IEEE floating-point standard szerinti lebegőpontos számok.[49]
Kulturális vonatkozások[szerkesztés]
Az internet növekedésével a 0,999…-ről szóló viták kiszabadultak az osztálytermekből, és helyet foglaltak a hírcsoportokban és a fórumokban, még azokban is, amelyeknek elvben semmi közük sincs a matematikához. A sci.math hírcsoportban népszerű időtöltéssé vált a 0,999…-ről érvelni, és erre a kérdésre a hírcsoport FAQ (gyakori kérdések) fejezetében is kitérnek.[50] A FAQ foglalkozik az ⅓-dal, a 10-zel való szorzással, a határértékekkel és a Cauchy-sorozatokkal.
Az általános érdeklődéssel kísért The Straight Dope 2003-as kiadása az ⅓-dal és a határértékekkel foglalkozik, és a félreértésekre is kitér.
A bennünk levő alsóbbrendű főemlős még mindig ellenáll, mondván: a 0,999… nem egy szám, hanem egy sor. Ahhoz, hogy egy számot találjunk, meg kell állítanunk, és akkor már 0,999~ = 1.
Ez nonszensz.[51]
A The Straight Dope idéz egy vitát, amely egy olyan üzenőfalról indult, amely leginkább videojátékokról szólt. Ugyanezzel a hévvel a 0,999… kérdése olyan népszerűvé vált a Blizzard Entertainment első hét évében a Battle.net fórumain, hogy Mike Morhaime, a vállalat elnöke sajtótájékoztatót tartott 2004. április 1-jén, hogy 0,999… = 1.
Nagy örömmel tölt el bennünket, hogy egyszer s mindenkorra lezárhatjuk ezt a fejezetet. Rengeteg fejfájásnak és aggodalomnak voltunk tanúi, hogy vajon 0,999… egyenlő-e vagy nem egyenlő 1-gyel, és most büszkén állíthatjuk, hogy a következő bizonyíték véglegesen és meggyőzően tárgyalja a kérdést ügyfeleink számára.[52]
Blizzard ezután két bizonyítást is közölt, amelyek a határértékeken és a 10-zel való szorzáson alapultak.
Jegyzetek[szerkesztés]
- ↑ Bunch p. 119; Tall and Schwarzenberger p. 6. Az utóbbi megjegyzés Burrelltől (p. 28): Talán a legmegbízhatóbb szám az 1, így különösen lesújtó, ha valaki a 0,999…-et 1-ként értelmezi.
- ↑ Tall és Schwarzenberger pp. 6–7; Tall 2000 p. 221
- ↑ Tall és Schwarzenberger p. 6; Tall 2000 p. 221
- ↑ Tall 2000 p. 221
- ↑ Tall 1976 pp. 10–14
- ↑ Pinto and Tall p. 5, Edwards és Ward pp. 416–417
- ↑ Mazur pp. 137–141
- ↑ Dubinsky et al. 261–262
- ↑ a b Vö. Ugyanezzel az érveléssel kettes számrendszerben: Silvanus P. Thompson: Calculus made easy. New York: St. Martin’s. 1998. ISBN 0-312-18548-0
- ↑ Rudin p. 61, Theorem 3.26; J. Stewart p. 706
- ↑ Euler 170. o.
- ↑ Kósa András: Ismerkedés a matematikai analízissel pp. 204, 210;
- ↑ Grattan-Guinness p. 69; Bonnycastle p. 177
- ↑ A határérték következik például Rudin p. 57, Theorem 3.20e.-ből. Direktebb megközelítéshez lásd Finney, Weir, Giordano (2001) Thomas' Calculus: Early Transcendentals 10ed, Addison-Wesley, New York. Section 8.1, example 2(a), example 6(b).
- ↑ Beals p. 22; I. Stewart p. 34
- ↑ Apostol p. 12
- ↑ A történelmi szintézis Griffiths és Hilton (p. xiv) nevéhez fűződik, 1970-ben, és Pugh (p. 10) 2001-ben; mindkettő előnyben részesíti a Dedekind-szeleteket az axiómákhoz képest. A szeletekhez lásd Pugh p. 17-et vagy Rudin p. 17-et; a logikához Pugh p. 10-et, Rudin p. ix-et vagy Munkres p. 30-at.
- ↑ Enderton p. 113
- ↑ Pontosabban, Rudin, Richman, és Enderton ezt a szeletet 1*, 1‒, és 1R szeletnek nevezi, amelyek mindegyike azonos az 1 valós számmal. Jegyezzük meg, hogy amit Rudin és Enderton Dedekind-szeletnek nevezett, azt Richman nem principális Dedekind-szeletnek hívta. Rudin pp. 17–20, Richman p. 399 vagy Enderton p. 119.
- ↑ Richman p. 399
- ↑ Griffiths & Hilton §24.2 "Sequences" p. 386
- ↑ A tizedes kifejtések fenti megközelítése a 0,999… = 1 bizonyításával együtt Griffiths & Hilton 1970 A comprehensive textbook of classical mathematics: A contemporary interpretation című művét követi. Griffiths & Hilton pp. viii, 395
- ↑ Petkovšek p. 408
- ↑ Protter és Morrey p. 503; Bartle and Sherbert p. 61
- ↑ Komornik és Loreti p. 636
- ↑ Petkovšek pp. 410–411
- ↑ Leavitt 1984 p. 301
- ↑ Lewittes pp. 1–3; Leavitt 1967 pp. 669, 673; Shrader-Frechette pp. 96–98
- ↑ Pugh p. 97; Alligood, Sauer, és Yorke pp. 150–152. Protter és Morrey (p. 507) és Pedrick (p. 29) gyakorló feladatként jelöli ezt a leírást.
- ↑ Maor (p. 60) és Mankiewicz (p. 151) az előbbi módszerhez; Mankiewicz Cantornak tulajdonítja, de az eredeti forrás tisztázatlan. Munkres (p. 50) említi az utóbbi módszert.
- ↑ Rudin p. 50, Pugh p. 98
- ↑ Gowers p. 60
- ↑ Berz 439–442
- ↑ John L. Bell (2003). „An Invitation to Smooth Infinitesimal Analysis” (PDF). (Hozzáférés: 2006. június 29.)
- ↑ A nem standard számok teljesebb leírásához lásd Robinson: Non-standard Analysis.
- ↑ Lightstone pp. 245–247. Nem vizsgálta a visszatérő kilenceseket a kifejtés standard részében.
- ↑ Berlekamp, Conway, és Guy (pp. 79–80, 307–311) 1-et, 1/3 -ot, és érinti 1/ω-t. A 0,111…-hez tartozó játék közvetlenül következik Berlekamp szabályából, és ezt tárgyalja A. N. Walker: Hackenstrings and the 0.999… 1 FAQ, 1999. [2006. június 16-i dátummal az eredetiből archiválva]. (Hozzáférés: 2006. június 29.)
- ↑ Richman pp. 397–399
- ↑ Richman pp. 398–400. Rudin (p. 23) ezt az alternatív konstrukciót a racionális számok felett tárgyalja az első fejezet utolsó gyakorlatában.
- ↑ Gardiner p. 98; Gowers p. 60
- ↑ a b Fjelstad p. 11
- ↑ Fjelstad pp. 14–15
- ↑ DeSua pp. 901–903
- ↑ Péter Rózsa: Játék a végtelennel. 9., jav. kiad. Budapest: Typotex. 2004. ISBN 978-963-279-092-3
- ↑ Péter Rózsa: Játék a végtelennel
- ↑ Példaként lásd J.B. Conway eljárását a Möbius-transzformációkon, pp. 47–57
- ↑ Maor p. 54
- ↑ Munkres p. 34, Exercise 1(c)
- ↑ Kroemer, Herbert; Kittel, Charles. Thermal Physics, 2e, W. H. Freeman, 462. o. (1980). ISBN 0-7167-1088-9
- ↑ Ahogy Richman (p. 396). megfigyelte. Hans de Vreught: sci.math FAQ: Why is 0.9999… = 1?, 1994. (Hozzáférés: 2006. június 29.)
- ↑ Cecil Adams: An infinite question: Why doesn't .999~ = 1?. The Straight Dope. The Chicago Reader, 2003. július 11. [2006. augusztus 15-i dátummal az eredetiből archiválva]. (Hozzáférés: 2006. szeptember 6.)
- ↑ Blizzard Entertainment® Announces .999~ (Repeating) = 1. Press Release. Blizzard Entertainment, 2004. április 1. [2007. január 20-i dátummal az eredetiből archiválva]. (Hozzáférés: 2006. szeptember 3.)
Fordítás[szerkesztés]
- Ez a szócikk részben vagy egészben a 0.999... című angol Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.
Források[szerkesztés]
- Alligood, Sauer, and Yorke. 4.1 Cantor Sets, Chaos: An introduction to dynamical systems. Springer (1996). ISBN 0-387-94677-2
- Apostol, Tom M.. Mathematical analysis, 2e, Addison-Wesley (1974). ISBN 0-201-00288-4
- Bartle, R.G. and D.R. Sherbert. Introduction to real analysis. Wiley (1982). ISBN 0-471-05944-7
- Beals, Richard. Analysis. Cambridge UP (2004). ISBN 0-521-60047-2
- Berlekamp, E.R.; J.H. Conway; and R.K. Guy. Winning Ways for your Mathematical Plays. Academic Press (1982). ISBN 0-12-091101-9
- Berz, Martin (1992). „Automatic differentiation as nonarchimedean analysis”. Computer Arithmetic and Enclosure Methods: 439–450, Elsevier.
- Bunch, Bryan H.. Mathematical fallacies and paradoxes. Van Nostrand Reinhold (1982). ISBN 0-442-24905-5
- Burrell, Brian. Merriam-Webster's Guide to Everyday Math: A Home and Business Reference. Merriam-Webster (1998). ISBN 0-87779-621-1
- Conway, John B.. Functions of one complex variable I, 2e, Springer-Verlag [1973] (1978). ISBN 0-387-90328-3
- Davies, Charles. The University Arithmetic: Embracing the Science of Numbers, and Their Numerous Applications. A.S. Barnes (1846)
- DeSua, Frank C. (1960. November). „A system isomorphic to the reals”. The American Mathematical Monthly 67, 900–903. o. DOI:10.2307/2309468.
- Dubinsky, Ed, Kirk Weller, Michael McDonald, and Anne Brown (2005). „Some historical issues and paradoxes regarding the concept of infinity: an APOS analysis: part 2”. Educational Studies in Mathematics 60, 253–266. o. DOI:10.1007/s10649-005-0473-0.
- Edwards, Barbara and Michael Ward (2004. May). „Surprises from mathematics education research: Student (mis)use of mathematical definitions” (PDF). The American Mathematical Monthly 111, 411–425. o. DOI:10.2307/4145268.
- Enderton, Herbert B.. Elements of set theory. Elsevier (1977). ISBN 0-12-238440-7
- Euler, Leonhard.szerk.: John Hewlett and Francis Horner, English translators.: Elements of Algebra, 3rd English, Orme Longman [1770] (1822)
- Fjelstad, Paul (1995. January). „The repeating integer paradox”. The College Mathematics Journal 26, 11–15. o. DOI:10.2307/2687285.
- Gardiner, Anthony. Understanding Infinity: The Mathematics of Infinite Processes. Dover [1982] (2003). ISBN 0-486-42538-X
- Gowers, Timothy. Mathematics: A Very Short Introduction. Oxford UP (2002). ISBN 0-19-285361-9
- Grattan-Guinness, Ivor. The development of the foundations of mathematical analysis from Euler to Riemann. MIT Press (1970). ISBN 0-262-07034-0
- Griffiths, H.B., P. J. Hilton. A Comprehensive Textbook of Classical Mathematics: A Contemporary Interpretation. London: Van Nostrand Reinhold. LCC QA37.2 G75 (1970). ISBN 0-442-02863-6
- Kempner, A.J. (1936. December). „Anormal Systems of Numeration”. The American Mathematical Monthly 43, 610–617. o. DOI:10.2307/2300532.
- Komornik, Vilmos; and Paola Loreti (1998). „Unique Developments in Non-Integer Bases”. The American Mathematical Monthly 105, 636–639. o. DOI:10.2307/2589246.
- Leavitt, W.G. (1967). „A Theorem on Repeating Decimals”. The American Mathematical Monthly 74, 669–673. o. DOI:10.2307/2314251.
- Leavitt, W.G. (1984. September). „Repeating Decimals”. The College Mathematics Journal 15, 299–308. o. DOI:10.2307/2686394.
- Lewittes, Joseph: Midy's Theorem for Periodic Decimals. New York Number Theory Workshop on Combinatorial and Additive Number Theory. arXiv, 2006
- Lightstone, A.H. (1972. March). „Infinitesimals”. The American Mathematical Monthly 79, 242–251. o. DOI:10.2307/2316619.
- Mankiewicz, Richard. The story of mathematics. Cassell (2000). ISBN 0-304-35473-2
- Maor, Eli. To infinity and beyond: a cultural history of the infinite. Birkhäuser (1987). ISBN 3-7643-3325-1
- Mazur, Joseph. Euclid in the Rainforest: Discovering Universal Truths in Logic and Math. Pearson: Pi Press (2005). ISBN 0-13-147994-6
- Munkres, James R.. Topology, 2e, Prentice-Hall [1975] (2000). ISBN 0-13-181629-2
- Núñez, Rafael (2006). „Do Real Numbers Really Move? Language, Thought, and Gesture: The Embodied Cognitive Foundations of Mathematics”. 18 Unconventional Essays on the Nature of Mathematics: 160–181, Springer. [2011. július 18-i dátummal az eredetiből archiválva]. ISBN 978-0-387-25717-4. Hozzáférés: 2009. augusztus 22.
- Pedrick, George. A First Course in Analysis. Springer (1994). ISBN 0-387-94108-8
- Petkovšek, Marko (1990. May). „Ambiguous Numbers are Dense”. American Mathematical Monthly 97, 408–411. o. DOI:10.2307/2324393.
- Pinto, Márcia and David Tall (2001). „Following students' development in a traditional university analysis course” (PDF). PME25: v4: 57–64. Hozzáférés: 2009. május 3.
- Protter, M.H. and C.B. Morrey. A first course in real analysis, 2e, Springer (1991). ISBN 0-387-97437-7
- Pugh, Charles Chapman. Real mathematical analysis. Springer-Verlag (2001). ISBN 0-387-95297-7
- Renteln, Paul and Allan Dundes (2005. January). „Foolproof: A Sampling of Mathematical Folk Humor” (PDF). Notices of the AMS 52, 24–34. o. (Hozzáférés: 2009. május 3.)
- Richman, Fred (1999. December). „Is 0.999… = 1?”. Mathematics Magazine 72 (5), 396–400. o. Free HTML preprint: Richman, Fred: Is 0.999… = 1?, 1999. június 8. [2006. február 3-i dátummal az eredetiből archiválva]. (Hozzáférés: 2006. augusztus 23.) Note: the journal article contains material and wording not found in the preprint.
- Robinson, Abraham. Non-standard analysis, Revised, Princeton University Press (1996). ISBN 0-691-04490-2
- Rosenlicht, Maxwell. Introduction to Analysis. Dover (1985). ISBN 0-486-65038-3
- Rudin, Walter. Principles of mathematical analysis, 3e, McGraw-Hill [1953] (1976). ISBN 0-07-054235-X
- Shrader-Frechette, Maurice (1978. March). „Complementary Rational Numbers”. Mathematics Magazine 51, 90–98. o.
- Smith, Charles and Charles Harrington. Arithmetic for Schools. Macmillan (1895)
- Sohrab, Houshang. Basic Real Analysis. Birkhäuser (2003). ISBN 0-8176-4211-0
- Stewart, Ian. The Foundations of Mathematics. Oxford UP (1977). ISBN 0-19-853165-6
- Stewart, James. Calculus: Early transcendentals, 4e, Brooks/Cole (1999). ISBN 0-534-36298-2
- D.O. Tall and R.L.E. Schwarzenberger (1978). „Conflicts in the Learning of Real Numbers and Limits” (PDF). Mathematics Teaching 82, 44–49. o. (Hozzáférés: 2009. május 3.)
- Tall, David (1976/7). „Conflicts and Catastrophes in the Learning of Mathematics” (PDF). Mathematical Education for Teaching 2, 2–18. o. (Hozzáférés: 2009. május 3.)
- Tall, David (2000). „Cognitive Development In Advanced Mathematics Using Technology” (PDF). Mathematics Education Research Journal 12, 210–230. o. (Hozzáférés: 2009. május 3.)
- von Mangoldt, Dr. Hans. Reihenzahlen, Einführung in die höhere Mathematik, 1st (német nyelven), Leipzig: Verlag von S. Hirzel (1911)
- Wallace, David Foster. Everything and more: a compact history of infinity. Norton (2003). ISBN 0-393-00338-8
- Bognárné, Nemetz , Tusnády. Ismerkedés a véletlennel, Középiskolai szakköri füzet
- Graham, R. L., D. E. Knuth, O. Patashnik. Konkrét matematika : a számítástudomány alapja. Budapest: Műszaki Könyvkiadó (1998)
- Kósa András. Ismerkedés a matematikai analízissel. Budapest: Műszaki Könyvkiadó (1981). ISBN 963-10-3820-3
- Kós Géza. Hogyan fogjunk oroszlánt?. KöMaL. Hozzáférés ideje: 2009. szeptember 23.
- Környei Imre, Turán Pál. Algebra. Budapest: Tankönyvkiadó Vállalat (1990)
- Mankiewicz, Richard. A matematika históriája. HVG könyvek (2003). ISBN 9637525300. Hozzáférés ideje: 2009. szeptember 23.[halott link]
- Pálfalvi Józsefné. Valós számok mint végtelen tizedestörtek, Matematika didaktikusan (2000). Hozzáférés ideje: 2009. szeptember 23.
- Péter Rózsa. Játék a végtelennel. Typotex (1999). ISBN 963 9132 47 0. Hozzáférés ideje: 2009. szeptember 23.
- Rudin, Walter. A matematikai analízis alapjai, Antos Péter, Somogyi Péter, Szabados Tamás (ford.), Budapest: Műszaki (1978)
- Stewart, Ian. A végtelen megszelídítése, Körmendi, Ágnes (ford.), Helikon Kiadó Kft (2008). ISBN 9789632271699
- Surányi László. A valós számok dedekind szeleteiről, Bolyai János forradalma. Surányi László honlapja. Hozzáférés ideje: 2009. szeptember 23.
- Urbán János. Határértékszámítás. Példatár. Mozaik Kiadó
További információk[szerkesztés]
- .999999… = 1? from cut-the-knot (angolul)
- Why does 0.9999… = 1 ? (angolul)
- Ask A Scientist: Repeating Decimals (angolul)
- Proof of the equality based on arithmetic (angolul)
- Repeating Nines (angolul)
- Point nine recurring equals one (angolul)
- David Tall's research on mathematics cognition (angolul)
- Warum 0,999 Periode nicht kleiner als 1 ist[halott link] (németül)
























![{\displaystyle [0;1],\quad [1;2],\quad [2;3],\dots ,\quad [9;10]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf48bbe2cfbcf007889d6f631e8c059856beb81e)








