Tizenkétszög
| Tizenkétszög | |
| Általános tizenkétszög | |
| Élek, csúcsok száma | 12 |
| Átlók száma | 54 |
| Belső szögek összege | 1800° |
| Szabályos tizenkétszög | |
 | |
| Schläfli-szimbólum | {12} |
| Szimmetriacsoport | diédercsoport (D12) |
| Terület: egységnyi oldalra | 11,196152 |
| Belső szög | 150° |
A geometriában a tizenkétszög egy tizenkétoldalú sokszög.
A szabályos sokszögek szögeire ismert képlet n=12 esetben a következőt adja:
tehát a szabályos tizenkétszög belső szögei 150 fokosak.
A szabályos tizenkétszög szerkesztése[szerkesztés]
A szabályos tizenkétszög szerkeszthető körzővel és vonalzóval.
Az alábbi animáció egy 23 lépéses szerkesztést mutat be. Vegyük észre, hogy a körzőnyílás nem változik 8. és a 11. lépés között.
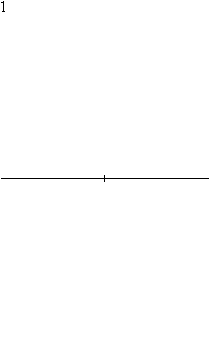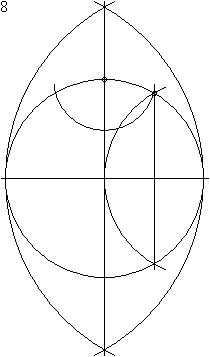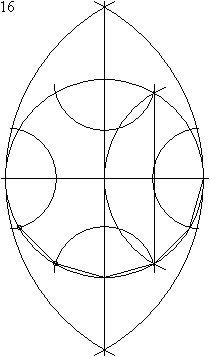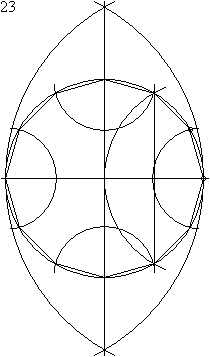
Terület[szerkesztés]
A szabályos sokszögek területére ismert képlet a oldalhosszra n=12 esetben:
ami a köré írt kör sugarának (R) függvényében a következőképpen alakul n=12 esetben:
a beírt kör sugarának (r) függvényeként pedig így:
A sík lefedése (csempézés)[szerkesztés]
Szabályos tizenkét szögeket használnak fel az alábbi periodikus csempézések:

|

|

|

|

|

|
Felhasználása[szerkesztés]
- Az ausztrál 50 centes, a fidzsi-szigeteki 50 centes, a tongani 50 seniti és a salamon-szigeteki 50 centes érmék szabályos tizenkétszög alakúak. A horvát kuna 25-ös érméje szintén. 2005 júliusig a román 5000 lejes érme szintén tizenkétszögletű volt. A kanadai penny érme is tizenkétszög alakú volt 1982 és 1996 között valamint a dél-vietnami 20 Ðong érme 1975-ig. A zambiai 50 ngwee (1992-ig) és a malawi 50 tambala (1995-ig) tizenkétszögletű volt. A mexikói 20 centes érme is tizenkétszög.
Lásd még[szerkesztés]
Külső hivatkozások[szerkesztés]
- Dodecagon and Kurschak's Tile and Theorem by Antonio Gutierrez from "Geometry Step by Step from the Land of the Incas"
- Weisstein, Eric W.: Dodecagon (angol nyelven). Wolfram MathWorld
- Kürschak's Tile and Theorem
- A tizenkétszög tulajdonságia animációval




