Savi disszociációs állandó

A Ka savi disszociációs állandó egy sav oldatbeli erősségének kvantitatív mértéke, a savak disszociációjának egyensúlyi állandója. Az egyensúlyt az alábbi módon írhatjuk fel:
- HA ⇌ A− + H+,
ahol HA egy általános sav, amelyből disszociáció során A− –a sav konjugált bázisa–, valamint egy hidrogénion (proton; H+) keletkezik, mely vizes oldatokban akvatált oxóniumion formájában létezik.
Az ábrabeli példán a HA az ecetsav, A− az acetátion. Ha a HA, A− és H+ részecskék egyensúlyban vannak, azt jelenti, hogy a koncentrációjuk nem változik az idő múlásával. A disszociációs állandót (mely a K egyensúlyi állandó a sav-bázis reakciókra vonatkoztatva) a [HA], [A−] és [H+] jelölésű egyensúlyi koncentrációk hányadosaként írják fel (a tört számlálójában a termék(ek) koncentrációjának szorzatával, a nevezőben pedig a kiindulási anyag(ok) koncentrációjának szorzatával):
Mivel Ka értéke több nagyságrendet átfoghat, ezért a gyakorlatban gyakran a savi disszociációs állandó tízes alapú logaritmusát használják. A −log10 Ka-val egyenlő pKa-t is szokták savi disszociációs állandónak nevezni:
A disszociáció mértéke annál kisebb, minél nagyobb pKa értéke. A gyenge savak pKa értéke vízben körülbelül a −2 és 12 közötti tartományba esik. A körülbelül −2-nél kisebb pKa értékű savakat erős savaknak nevezzük. Az erős savak híg vizes oldatukban csaknem teljesen disszociálnak: ezekben a nem disszociált sav szinte kimutathatatlanná válik. Erős savak pKa értéke megbecsülhető elméleti úton, vagy extrapolálható olyan nem vizes oldószerekben végzett mérésekből, amelyekben a disszociációs állandó kisebb – ilyen oldószer például az acetonitril és a dimetil-szulfoxid.
A savak savi disszociációs állandója közvetlen következménye a disszociációs reakció termodinamikájának: a pKa értéke egyenesen arányos a reakció standard szabadentalpia változásával. pKa értéke függ a hőmérséklettől, ez kvalitatíven a Le Chatelier-elv alapján magyarázható: ha a reakció endoterm, a pKa értéke a hőmérséklet növelésével csökken, míg exoterm reakció esetén ennek a fordítottja érvényes. A savi disszociációs állandó nagyságát befolyásoló tényezők közé tartozik Pauling savak erősségét taglaló szabályai, az induktív és mezomer effektusok, valamint a hidrogénkötés.
A savak és bázisok oldatbeli pontos viselkedése csak akkor érthető meg, ha pKa értéke ismert. Különösen igaz ez a pH-ra, melynek értéke akkor számítható ki, ha minden sav és bázis analitikai koncentrációja és pKa értéke ismert. Megfordítva: a savak és bázisok oldatbeli egyensúlyi koncentrációját ki lehet számítani, ha ismert a pH. Ezeket a számításokat a kémia, biológia, orvostudomány és geológia számos területén alkalmazzák. Például számos, a gyógyászatban használt anyag gyenge sav vagy bázis, melyek pKa értéke és a víz–oktanol megoszlási hányadosának ismeretében megbecsülhető, hogy az adott vegyület mekkora hányada kerül be a véráramba. A savi disszociációs állandó ismerete nélkülözhetetlen a vízkémiában és a kémiai oceanográfiában, ahol a víz savassága alapvető szerepet játszik. Az élő szervezetekben a sav-bázis homeosztázis és az enzimek kinetikája a sejtben és testben jelen levő számos sav és bázis pKa értékétől függ. A kémiában a pufferoldatok készítéséhez szükséges a pKa ismerete, de a fémionok és savak vagy bázisok közötti – komplexek képződésével járó – kölcsönhatás kvantitatív értelmezéséhez is tudni kell a pKa értékét. A pKa kísérletileg potenciometriás titrálással határozható meg, de a kb. 2-nél kisebb vagy kb. 11-nél nagyobb pKa érték esetén a pH mérés gyakorlati nehézségei miatt spektrofotometriás vagy mágneses magrezonanciás mérés válhat szükségessé.
Definíciók
[szerkesztés]Arrhenius eredeti definíciója szerint a sav olyan anyag, mely vizes oldatban H+ hidrogénion (proton) leadása közben disszociál:[1]
- HA ⇌ A− + H+.
Ennek a disszociációs reakciónak az egyensúlyi állandója a disszociációs állandó.
A leadott proton egy vízmolekulával egyesülve H3O+ oxóniumiont képez, ezért Arrhenius később javasolta, hogy a disszociációt sav-bázis reakcióként írják fel:
- HA + H2O ⇌ A− + H3O+.
A Brønsted–Lowry sav-bázis elmélet tovább általánosítva protoncsere reakciókról beszél:[2][3][4]
- sav + bázis ⇌ konjugált bázis + konjugált sav.
A sav protont ad le és konjugált bázissá alakul, miközben a protont felveszi a bázis, amely így konjugált savvá alakul. Egy HA sav vizes oldatában a bázis a víz, a konjugált bázis az A− és a konjugált sav az oxóniumion. A Brønsted–Lowry definíció más oldószerekre is alkalmazható, például dimetil-szulfoxidra: az S oldószer – a bázis – protont vesz fel és konjugált savvá (SH+) alakul.
Az oldatkémiában – az oldószertől függetlenül – gyakran használják a H+ rövidítést a szolvatált hidrogénion jelölésére.
Vizes oldatban a H+ nem protont, hanem szolvatált oxóniumiont jelöl.[5][6]
Egy sav vagy bázis konjugáltnak jelölése szövegfüggő. Egy B bázis BH+ konjugált savja a
- BH+ + OH− ⇌ B + H2O
egyenlet szerint disszociál, ami a
- H2O (sav) + B (bázis) ⇌ OH− (konjugált bázis) + BH+ (konjugált sav)
egyensúly fordítottja.
Az OH− hidroxidion – mely jól ismert bázis – a fenti reakcióban a víznek, mint savnak a konjugált bázisa. A savakat és bázisokat ezért egyszerűen csak protondonoroknak, illetve -akceptoroknak tekintjük.
A víz amfoter : savként és bázisként is reagálhat. További példa amfoter molekulára a hidrogén-karbonátion (HCO−3), amely a szénsav molekula (H2CO3) konjugált bázisa a
- H2CO3 + H2O ⇌ HCO−3 + H3O+
egyensúlyban, ugyanakkor a karbonátion (CO2−3) konjugált savja a
- HCO−3 + OH− ⇌ CO2−3 + H2O
reakciónak (ha az alsó nyíl irányába lejátszódó folyamatot tekintjük). A szénsav egyensúlyi reakciói fontosak az emberi test sav-bázis homeosztázisa szempontjából. A savi disszociáció tágabb definíciójába beletartozik a hidrolízis, melynek során protonok keletkeznek a vízmolekulák felhasadása során. Például a bórsav (B(OH)3), bár nem protondonor, mégis gyenge savként viselkedik az alábbi hidrolitikus egyensúly miatt:
- B(OH)3 + 2 H2O ⇌ B(OH)−4 + H3O+.
Hasonló módon a fémionok – például a [Al(H2O)6]3+) – hidrolízisük révén gyenge savként viselkednek:[7]
- [Al(H2O)6]3+ +H2O ⇌ [Al(H2O)5(OH)]2+ + H3O+.
Egyensúlyi állandó
[szerkesztés]A savi disszociációs állandó az egyensúlyi állandó egyik speciális példája. Egy adott egyértékű HA sav és A− konjugált bázisa között vízben fennálló
- HA + H2O ⇌ A− + H3O+
egyensúly K⊖ termodinamikai egyensúlyi állandója így definiálható:[8]
ahol {A} az A kémiai részecske aktivitása. Mivel az aktivitásnak nincs dimenziója, K⊖ dimenzió nélküli mennyiség. A disszociációs termékek aktivitásának szorzata a számlálóban, a reaktánsok aktivitásának szorzata a nevezőben szerepel.

Mivel az aktivitás a koncentráció és az aktivitási együttható (γ) szorzata, a fenti definíció felírható az alábbi formában is:
ahol [HA] a HA koncentrációját, Γ pedig az aktivitási együtthatók hányadosát jelöli.
Hogy kiküszöböljék az aktivitás alkalmazásából származó nehézségeket, a disszociációs együtthatókat, amikor lehetséges, nagy ionerősségű közegben határozzák meg, azaz olyan körülmények között, amikor Γ mindig állandónak vehető.[8] Ilyen közeg lehet például a 0,1 M nátrium-nitrát vagy 3 M kálium-perklorát oldat (1 M = 1 mol·dm−3, a moláris koncentráció mértékegysége). Ezen kívül – a legtöményebb oldatok kivételével – feltételezhető, hogy a víz koncentrációja – [H2O] – állandó, körülbelül 55 mol·dm−3. K⊖-t elosztva a konstans tagokkal, és az oxóniumion koncentrációját [H+]-val jelölve az alábbi kifejezést kapjuk:
- .
Ez az általánosan használt definíció.[9] A pKa-t mint −log10 Ka-t definiálják.
Ugyanakkor megjegyzendő, hogy az irodalomban közölt disszociációs állandók arra az adott közegre vonatkoznak, melyben a meghatározást végezték: a különböző körülmények között kapott értékek eltérnek egymástól, amint azt az ecetsavra mutatja a fenti illusztráció. Ha az irodalomban szereplő állandók más ionerősségre vonatkoznak, mint amely egy adott alkalmazáshoz szükséges, akkor ezek értékét a Brönstedt–Guggenheim–Scatchard-modell[10] (specific ion theory, SIT) vagy más elméletek segítségével korrigálni lehet.[11]
Noha úgy tűnhet, hogy Ka-nak koncentráció dimenziója van, valójában dimenzió nélküli mennyiség, ellenkező esetben nem lehetne a logaritmusát venni. A látszólagos ellentmondást az okozza, hogy a definiáló kifejezésből hiányzik a [H2O] állandó. Nem ritka azonban, hogy – különösen biokémiai egyensúlyokkal kapcsolatos szövegekben – dimenzióval megadott mérőszám szerepel, például „Ka = 300 M”.
Egyértékű savak
[szerkesztés]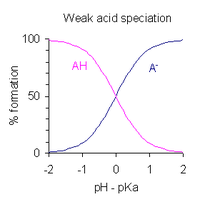
A Ka-t definiáló kifejezést átrendezve, és behelyettesítve a pH = −log10[H+] tagot, az alábbi összefüggéshez jutunk:
Ez a Henderson–Hasselbalch-egyenlet egyik formája, amely alapján az alábbi következtetések vonhatók le:
- Mivel 50%-os titráltságnál [AH]/[A−] = 1, és log(1) = 0, ezért 50%-os titráltságnál a pH megegyezik a pKa számértékével. Fordítva is igaz, hogy amikor pH = pKa, akkor AH és A− koncentrációja egyenlő.
- A puffertartomány körülbelül a pH = pKa ± 2 tartományra terjed ki, de a pufferelési képesség gyenge a pKa ± 1 tartományon kívül. pKa ± 1 esetén [AH]/[A−] = 10 vagy 1/10.
- Ha a pH ismert, akkor az [AH]/[A−] arányt ki lehet számítani. Ez az arány független a sav analitikai koncentrációjától.
Vízben a pKa meghatározható tartománya az erős savak mintegy −2-es értékétől a nagyon gyenge savak (vagy erős bázisok) kb. 12-es értékéig tart. Minden sav, melynek pKa-ja −2-nél kisebb, 99%-nál nagyobb mértékben disszociál 0-s pH-n (1 M savkoncentrációnál). Ez mint az oldószer kiegyenlítő hatása ismert, mivel minden ilyen sav a pKa-tól függetlenül ugyanolyan mértékben erős savként viselkedik. Hasonló módon minden bázis, melyre pKa nagyobb, mint a felső határérték, több mint 99%-ban deprotonált állapotban van jelen az oldatban minden elérehtő pH esetén, ezeket erős bázisnak nevezzük.[3]
Erős savra példa a hidrogén-klorid (HCl), melynek vízben a termodinamikai mennyiségekből becsült pKa-ja −9,3.[12] 1 mol·dm−3-es oldatban a nem disszociált sav koncentrációja kevesebb, mint 0,01%-a a disszociációs termékek koncentrációjának. Azt mondjuk, hogy a sósav vizes oldatban „teljesen disszociál”, mivel a nem disszociált sav mennyisége nem érzékelhető. Ha egy egyértékű sav pKa-ja és analitikai koncentrációja ismert, akkor a disszociáció mértéke és az oldat pH-ja egyszerűen kiszámítható..
Kívánt pH-jú pufferoldatot gyenge sav és konjugált bázisának elegyítésével készíthető. A gyakorlatban az elegyet lehet úgy készíteni, hogy a savat feloldjuk vízben, majd hozzáadjuk a szükséges mennyiségű erős savat vagy bázist. A sav pKa-ja a kívánt pH értéktől legfeljebb két egységgel különbözhet.
Többértékű savak
[szerkesztés]
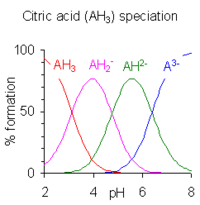
A többértékű savak olyan savak, amelyek egynél több proton leadására képesek. Az első proton disszociációs állandóját Ka1, a következő protonét Ka2 stb. jelölheti. Többértékű savra példa a foszforsav, amely három proton leadására képes.
egyensúly pKa értéke H3PO4 ⇌ H2PO−4 + H+ pKa1 = 2,15 H2PO−4 ⇌ HPO2−4 + H+ pKa2 = 7,20 HPO2−4 ⇌ PO3−4 + H+ pKa3 = 12,37
Ha az egyes pK-k között a különbség kb. négynél több, mint ebben a példában is, akkor minden egyes részecske önálló savnak tekinthető.[13] Valóban, a H2PO−4 sói kikristályosíthatók, ha az oldat pH-ját kb. 5,5-re állítjuk, míg a HPO2−4 sók mintegy 10-es pH-jú oldatból kristályosíthatók ki. A részecskék eloszlását ábrázoló diagramon látható, hogy a két ion koncentrációja 5,5-ös és 10-es pH-nál a legnagyobb.
Ha az egymást követő pK értékek között a különbség kevesebb, mint kb. négy, akkor átfedés van azon pH tartományok között, amelyekben az egyensúlyban részt vevő különböző részecskék léteznek. Minél kisebb a különbség, annál nagyobb az átfedés. Jobb oldalt a citromsav példája látható: a citromsav oldatok a teljes 2,5–7,5 pH tartományon belül pufferelnek.
Általában igaz, hogy az egymást követő pK értékek növekednek (Pauling első szabálya).[14] Például egy H2A kétértékű sav egyensúlyai a következők:
- H2A ⇌ HA− + H+
- HA− ⇌ A2− + H+
Látható, hogy a második protont egy negatívan töltött részecske adja le. Mivel a proton töltése pozitív, ezért plusz munka szükséges az eltávolításához – ez okozza a fent említett tendenciát. A foszforsavra (fentebb) megadott értékek - a H3VO4 vanádiumsavra kapott értékekhez hasonlóan - példázzák ezt a szabályt. Ha a szabály alól kivételt találunk, akkor az a szerkezetben bekövetkező jelentős változásra utal. A VO+2(aq) esetében a vanádium 6-os koordinációjú, oktaéderes elrendeződésű, míg a vanádiumsav tetraéderes, 4-es koordinációjú. Ez az alapja annak magyarázatának, hogy a vanádium(V) oxosavaknál pKa1 miért nagyobb mint pKa2.
egyensúly pKa értéke [VO2(H2O)4]+ ⇌ H3VO4 + H+ + 2H2O pKa1 = 4,2 H3VO4 ⇌ H2VO−4 + H+ pKa2 = 2,60 H2VO−4 ⇌ HVO2−4 + H+ pKa3 = 7,92 HVO2−4 ⇌ VO3−4 + H+ pKa4 = 13,27
A víz autoprotolízise
[szerkesztés]A víz savként és bázisként is viselkedhet. A
- 2 H2O ⇌ OH− + H3O+
egyensúly egyensúlyi állandóját az alábbi kifejezés adja meg:
Amennyiben a víz koncentrációja állandónak vehető – ami általában teljesül –, akkor a fenti kifejezést az alábbival helyettesíthetjük:
Kw értéke standard hőmérsékleten és nyomáson 1,0·10−14. A Kw vízionszorzat tehát csak a savi disszociációs állandó egyik különleges esete.
Bázisok
[szerkesztés]Történetileg a bázisok Kb egyensúlyi állandóját a B bázis protonálódásának asszociációs állandójaként definiálták, amikor is a konjugált sav, HB+ keletkezik.
- B + H2O ⇌ HB+ + OH−
A fentiekhez hasonló gondolatmenet alapján:
Vízben a hidroxidionok [OH−] koncentrációja kapcsolatban van a hidrogénion koncentrációval: Kw = [H+] [OH−], ezért
Kb kifejezésébe beírva [OH−] kifejezését az alábbi egyenletet kapjuk:
Ha Ka, Kb és Kw azonos hőmérséklet és ionerősség mellett lett meghatározva, akkor a kologaritmus alapján következik, hogy pKb = pKw − pKa. Vizes oldatban 25 °C-on pKw értéke 13,9965,[15] így pKb ≈ 14 − pKa.
Tulajdonképpen nincs arra szükség, hogy a pKa mellett külön definiáljuk a pKb-t, csak azért tettük meg, mert a régebbi irodalmakban még találkozhatunk pKb értékekkel.
Hőmérsékletfüggés
[szerkesztés]A van ’t Hoff-egyenlet szerint minden egyensúlyi állandó értéke függ a hőmérséklettől:[16]
R az egyetemes gázállandó, T a hőmérséklet kelvinben. Így exoterm reakció esetén (melyre a ΔH⊖ standardentalpia változás negatív) K csökken a hőmérséklet növelésével, de endoterm reakciónál (amikor ΔH⊖ pozitív) K a hőmérséklet emelésével nő.
Savasság nem vizes oldatokban
[szerkesztés]Az oldószerek valószínűleg jobban elősegítik az oldott savmolekulák disszociációját, ha fennállnak az alábbi körülmények:[17]
- Az oldószer hidrogénkötés kialakítására képes protikus oldószer.
- Az oldószer donorszáma magas, ezért erős Lewis-bázis.
- Az oldószer dielektromos állandója (relatív permittivitása) nagy, ami miatt jól oldja az ionos anyagokat.
Szerves vegyületek pKa értékét gyakran dimetil-szulfoxid (DMSO)[17] és acetonitril (AN) aprotikus oldószereket használva határozzák meg.[18]
| Oldószer | Donorszám[17] | Dielektromos állandó[17] |
|---|---|---|
| Acetonitril | 14 | 37 |
| Dimetil-szulfoxid | 30 | 47 |
| Víz | 18 | 78 |
A DMSO-t kiterjedten használják víz helyett, mivel dielektromos állandója a vízénél kisebb, és molekulája kevésbé poláris, emiatt a nem poláris, hidrofób anyagokat könnyebben oldja. A mérhető pKa tartománya kb. 1 és 30 közé esik. Az acetonitril a DMSO-nál kevésbé bázisos, így benne a savak általában gyengébbek, míg a bázisok többnyire erősebbek. Az alábbi táblázatokban meg van adva néhány 25 °C-on meghatározott pKa érték acetonitrilben (AN)[19][20][21] és dimetil-szulfoxidban (DMSO).[22] Összehasonlításként a vízre vonatkozó értékek is meg vannak adva.
| HA ⇌ A− + H+ | AN | DMSO | víz |
|---|---|---|---|
| p-toluolszulfonsav | 8,5 | 0,9 | erős |
| 2,4-Dinitrofenol | 16,66 | 5,1 | 3,9 |
| Benzoesav | 21,51 | 11,1 | 4,2 |
| Ecetsav | 23,51 | 12,6 | 4,756 |
| Fenol | 29,14 | 18,0 | 9,99 |
| BH+ ⇌ B + H+ | |||
| Pirrolidin | 19,56 | 10,8 | 11,4 |
| Trietil-amin | 18,82 | 9,0 | 10,72 |
| Protonszivacs | 18,62 | 7,5 | 12,1 |
| Piridin | 12,53 | 3,4 | 5,2 |
| Anilin | 10,62 | 3,6 | 9,4 |
Savas oldószerben a savak ionizációja kisebb mértékű, mint vízben. Például a hidrogén-klorid gyenge savként viselkedik, ha ecetsavban oldjuk. Ennek az az oka, hogy az ecetsav a víznél jóval gyengébb bázis.
- HCl + CH3CO2H ⇌ Cl− + CH3C(OH)+2
- sav + bázis ⇌ konjugált bázis + konjugált sav
Hasonlítsuk össze ezt a reakciót azzal, hogy mi történik, amikor az ecetsavat a savasabb, tiszta kénsavban oldjuk:[23]
- H2SO4 + CH3CO2H ⇌ HSO−4 + CH3C(OH)+2
Ebben a környezetben a kétségtelenül valószínűtlen geminális diol szerkezetű CH3C(OH)+2 részecske stabil. Vizes oldatokban a legkényelmesebb savassági függvény a pH-skála.[24] Nem vizes közegekre további savassági függvényeket javasoltak, ezek közül legnevezetesebb a Hammett-féle savassági függvény (H0) a szupersavas, valamint módosított változata (H−) a szuperbázisos közegekre.[25]

Aprotikus oldószerekben hidrogénkötés révén oligomerek keletkezhetnek, ilyen például a jól ismert ecetsav dimer. Hidrogénkötés jöhet létre egy sav és a konjugált bázisa között is. Ez a homokonjugációnak nevezett folyamat növeli a savak erősségét, azaz csökkenti az effektív pKa értéküket azáltal, hogy stabilizálja a konjugált bázist. A homokonjugáció a toluolszulfonsav protondonáló képességét acetonitriles oldatban közel 800-szorosára növeli.[26] Vizes oldatban nem lép fel homokonjugáció, mivel a víz erősebb hidrogénkötést létesít a konjugált bázissal, mint a savval.
Oldószerkeverékek
[szerkesztés]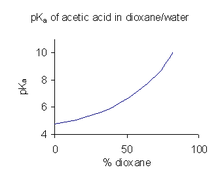
Ha egy vegyület vízben rosszul oldódik, akkor gyakori megoldás (például a gyógyszeriparban), hogy a pKa értékét egy olyan oldószerkeverékben – például víz/dioxán vagy víz/metanol elegyben – határozzák meg, amelyben jobb a vegyület oldhatósága.[28] A jobb oldalon látható példában pKa értéke meredeken emelkedik, ahogy nő a dioxán aránya, mivel a keverék dielektromos állandója csökken.
Az oldószerkeverékben mért pKa közvetlenül nem alkalmazható vizes oldatokra. Ennek az az oka, hogy amikor az oldószer standard állapotban van, akkor az aktivitása definíció szerint egy. Például a víz:dioxán 9:1 keverék standard állapota pontosan az ilyen arányú elegy, oldott anyag nélkül. Ahhoz, hogy vizes oldatokra használható pKa értéket kapjunk, a különböző összetételű oldószerkeverékre kapott értékeket kell extrapolálnunk a segédoldószer nulla koncentrációjára.
Ezeket a tényeket elfedi a pKa definiálására használt egyenlet, mivel abból kimarad az oldószer aktivitása. Egy adott oldószerkeverékben kapott pKa értékek azonban összehasonlíthatók egymással, ami megadja a savak relatív erősségét. Ugyanez igaz egy adott nem vizes oldószerben, például DMSO-ban meghatározott pKa értékekre is.
A tudomány 2008-as állása szerint nincs kidolgozva univerzális, oldószerfüggetlen skála a savi disszociációs állandókra, mivel nincs ismert módszer két különböző oldószer standard állapotának összehasonlítására.
A pKa értékét befolyásoló tényezők
[szerkesztés]Pauling második szabálya szerint egy XOm(OH)n összetételű sav első pKa-ja közelítőleg független n-től és X-től, és értéke m = 0 esetén közelítőleg 8; m = 1-nél 2; m = 2-nél −3 és m = 3 esetén < −10.[14] Ez összefüggésben van az X központi atom oxidációs állapotával: minél nagyobb az oxidációs fok, annál erősebb a sav. Például a HClO pKa-ja 7,2; a HClO2-é 2,0; a HClO3-é −1; a HClO4 pedig erős sav.



Szerves savak esetén az induktív- és mezomer-effektus befolyásolja a pKa értékét. Egyszerű példát kapunk, ha az ecetsav hidrogénatomjait elektronegatívabb klóratomokra cseréljük ki. A szubsztituens elektronvonzó hatása megkönnyíti az ionizációt, így a pKa értékei 0, 1, 2 és 3 klóratom jelenléte esetén rendre 4,7; 2,8; 1,3 és 0,7.[29] A Hammett-egyenlet általános kifejezést szolgáltat a szubsztituensek hatásának leírására.[30]
- log Ka = log Ka0 + ρσ.
Ka a szubsztituált vegyület disszociációs állandója, Ka0 a disszociációs állandó hidrogén szubsztituens esetén, ρ a szubsztituálatlan vegyületre jellemző tulajdonság és σ minden egyes szubsztituensre adott értékkel rendelkezik. Ha log Ka-t ábrázoljuk σ függvényében, egy egyenest kapunk, melynek y-tengelymetszete logKa0 és meredeksége ρ. Ez a lineáris szabadenergia összefüggések egyik példája, mivel log Ka arányos a standard szabadenergia változással. Hammett eredetileg[31] különböző, orto és para helyzetben szubsztituált benzoesav-származékok adatai alapján alkotta meg az összefüggést. Ez és más vizsgálatok lehetővé tették, hogy a szubsztituenseket elektronvonzó vagy elektronküldő erősségük alapján sorba állítsák, és hogy megkülönböztessék az induktív és mezomer effektust.[32][33]
Az alkoholok rendes körülmények között vízben nem viselkednek savként, de az OH csoport mellett egy kettős kötés jelenléte a keto-enol tautoméria révén lényegesen csökkentheti a pKa értékét, erre példa az aszkorbinsav. A diketon 2,4-pentándion (acetilaceton) a keto-enol egyensúly következtében szintén gyenge savként viselkedik. OH szubsztituenst tartalmazó aromás vegyületekben, mint például a fenolban, az aromás gyűrűvel kialakuló konjugáció jelentősen stabilizálja a deprotonált formát.
Fontosak lehetnek a szerkezeti tényezők is, ennek klasszikus példája a fumársav és a maleinsav közötti különbség. A fumársav (E)-1,4-but-2-éndisav, transz-izomer, míg a maleinsav a cisz-izomernek felel meg, (Z)-1,4-but-2-éndisav (lásd cisz-transz izoméria). A fumársav pKa értékei közelítőleg 3,5 és 4,5, ezzel szemben a maleinsav pKa értékei körülbelül 1,5 és 6,5. A nagy különbség oka, hogy amikor a cisz-izomer (a maleinsav) lead egy protont, erős intramolekuláris hidrogénkötés alakul ki a két közeli karboxilcsoport között. Ez elősegíti a hidrogén-maleátion képződését, és gátolja a második proton leadását. A transz-izomerben a két karboxilcsoport mindig távol van egymástól, így közöttük nem alakul ki hidrogénkötés.[34]
A protonszivacs (1,8-bisz(dimetilamino)naftalin) pKa-értéke 12,1, az egyik legerősebb ismert amin bázis. Erős bázisosságát a protonálódás révén megszűnő feszültségnek és az erős belső hidrogénkötésnek tulajdonítják.[35][36]
Termodinamika
[szerkesztés]Az egyensúlyi állandó kapcsolatban van a reakció standard szabadentalpia változásával, így a savi disszociációs állandó esetén
- ΔG⊖ = 2,303 RT pKa.
R az egyetemes gázállandó és T a Kelvinben kifejezett hőmérséklet. Vegyük észre, hogy pKa= −log Ka és 2,303 ≈ ln 10. 25 °C-on ΔG⊖ kJ·mol−1-ban = 5,708 pKa (1 kJ·mol−1 = 1000 joule per mol). A szabadentalpia egy entalpia és egy entrópia tagot tartalmaz:[37]
- ΔG⊖ = ΔH⊖ − TΔS⊖
A standard entalpiaváltozás kalorimetriásan vagy a van ’t Hoff-egyenlet segítségével határozható meg, bár a kalorimetria a preferált módszer. Ha mind a standard entalpiaváltozás, mind a savi disszociációs állandó meg van határozva, akkor a standard entrópiaváltozás a fenti egyenlet alapján könnyen kiszámítható. Az alábbi táblázatban szereplő entrópia tagok kísérletileg meghatározott pKa és ΔH⊖ értékekből lettek kiszámítva. Az adatok kritikusan lettek kiválasztva, és 25 °C-os vízre vonatkoznak, nulla ionerősség mellett.[37]
| Vegyület | Egyensúly | pKa | ΔH⊖ /kJ·mol−1 | −TΔS⊖ /kJ·mol−1 |
|---|---|---|---|---|
| HA = Ecetsav | HA ⇌ H+ + A− | 4,756 | −0,41 | 27,56 |
| H2A+ = GlicinH+ | H2A+ ⇌ HA + H+ | 2,351 | 4,00 | 9,419 |
| HA ⇌ H+ + A− | 9,78 | 44,20 | 11,6 | |
| H2A = Maleinsav | H2A ⇌ HA− + H+ | 1,92 | 1,10 | 9,85 |
| HA− ⇌ H+ + A2− | 6,27 | −3,60 | 39,4 | |
| H3A = Citromsav | H3A ⇌ H2A− + H+ | 3,128 | 4,07 | 13,78 |
| H2A− ⇌ HA2− + H+ | 4,76 | 2,23 | 24,9 | |
| HA2− ⇌ A3− + H+ | 6,40 | −3,38 | 39,9 | |
| HA = Bórsav | HA ⇌ H+ + A− | 9,237 | 13,80 | 38,92 |
| H3A = Foszforsav | H3A ⇌ H2A− + H+ | 2,148 | −8,00 | 20,26 |
| H2A− ⇌ HA2− + H+ | 7,20 | 3,60 | 37,5 | |
| HA2− ⇌ A3− + H+ | 12,35 | 16,00 | 54,49 | |
| HA− = Hidrogén-szulfát | HA− ⇌ A2− + H+ | 1,99 | −22,40 | 33,74 |
| H2A = Oxálsav | H2A ⇌ HA− + H+ | 1,27 | −3,90 | 11,15 |
| HA− ⇌ A2− + H+ | 4,266 | 7,00 | 31,35 |
| Vegyület | Egyensúly | pKa | ΔH⊖ /kJ·mol−1 | −TΔS⊖ /kJ·mol−1 |
|---|---|---|---|---|
| B = Ammónia | HB+ ⇌ B + H+ | 9,245 | 51,95 | 0,8205 |
| B = Metil-amin | HB+ ⇌ B + H+ | 10,645 | 55,34 | 5,422 |
| B = Trietil-amin | HB+ ⇌ B + H+ | 10,72 | 43,13 | 18,06 |
Az első dolog, amit meg kell jegyezni, hogy amikor pKa pozitív, akkor a reakció standard szabadentalpia-változása szintén pozitív, azaz a gyenge savak disszociációja nem önként végbemenő folyamat. Másodszor, a reakciók egy része exoterm, másik része endoterm, de ha ΔH⊖ negatív, akkor elsősorban −TΔS⊖ határozza meg, hogy ΔG⊖ pozitív-e. Végezetül az is megállapítható, hogy ezeknél a reakcióknál az entrópia hozzájárulás mindig kedvezőtlen.
Megjegyzendő, hogy a reakció standard szabadentalpia-változása a standardállapotú reaktánsokból keletkező standardállapotú termékekre vonatkozik. A szabadentalpia-változás egyensúlyban nulla, mivel a reaktánsok és termékek kémiai potenciálja egyensúlyban azonos.
Kísérleti meghatározás
[szerkesztés]
A pKa értékeket kísérletileg rendszerint nagy ionerősségű közegben, állandó hőmérsékleten végzett titrálás segítségével határozzák meg.[38] A szokásos eljárásban a vegyület adott közegbeli oldatát erős savval annyira megsavanyítják, hogy a vegyület teljesen protonálódjon. Az oldatot ezután egy erős bázissal addig titrálják, amíg a vizsgált vegyület minden protont le nem ad. A titrálás minden pontjában mérik a pH-t, üvegelektród és pH-mérő segítségével. Az egyensúlyi állandót a számított pH-értékeknek a kísérleti eredményekhez történő illesztésével határozzák meg, a legkisebb négyzetek módszerének felhasználásával.[39]
A hozzáadott erős bázis teljes térfogatának a titrálandó oldat eredeti térfogatához képest kicsinek kell lennie, hogy az ionerősség értéke csaknem állandó maradjon. Ez biztosítja, hogy pKa értéke a titrálás folyamán ne változzon.
A jobb oldalon az oxálsav számított titrálási görbéje látható. Az oxálsav pKa értékei 1,27 és 4,27, így a puffertartomány nagyjából az 1,3–4,3-as pH tartományba esik. A puffertartomány tartalmazza a pKa meghatározásához szükséges információt, mivel a sav és konjugált bázisának koncentrációja a puffertartományon belül változik.
A két puffertartomány között található egy végpont vagy ekvivalenciapont, ahol a pH körülbelül két egységgel nő. Ez a végpont nem túl éles, ami jellemző az olyan kétértékű savakra, melyeknek a puffertartománya kis mértékben átfed: pKa2−pKa1 ebben a példában körülbelül három. (Ha a pK értékek különbsége körülbelül kettőnél kisebb lenne, akkor a végpont nem lenne látható.) A második végpont 6,3-as pH körül kezdődik, és éles. Ez azt jelzi, hogy a vegyület az összes protont leadta. Ilyen esetben nincs pufferhatás, és a pH meredeken emelkedik kis mennyiségű erős bázis hozzáadásakor. A pH azonban nem nő végtelenül nagyra: körülbelül 11-es pH (pKw − 3) körül egy új puffertartomány kezdődik. Ez az a pont, ahol a víz öndisszociációja jelentőssé kezd válni.
Vizes oldatban üvegelektróddal nagyon nehéz 2-es pH-nál kisebb értéket mérni, mivel a Nernst-egyenlet ilyen kis pH-knál már nem érvényes. A körülbelül 2-nél kisebb vagy 11-nél nagyobb pK értékek meghatározásához spektrofotometriás[40] vagy NMR[9][41] mérések használhatók a pH mérése helyett vagy annak kiegészítéseként.[42]
Amennyiben nem használható üvegelektród, mint például a nem vizes oldatoknál, akkor gyakran spektrofotometriás módszert alkalmaznak.[20] Ez lehet abszorbancia vagy fluoreszcencia mérés. Mindkét esetben feltételezzük, hogy a mért mennyiség arányos a fénnyel kölcsönható részecskefajták hozzájárulásának összegével, abszorbanciamérés esetén a Lambert–Beer-törvény használható.
Könnyűvizes oldatok nem alkalmasak 1H NMR mérésekhez, helyette nehézvizet (D2O) kell használni. 13C NMR adatok azonban felhasználhatók normál vízben, 1H NMR spektrumok pedig használhatók nem vizes közegekkel. Az NMR-rel a kémiai eltolódás időbeli átlaga mérhető volt, mivel a protoncsere az NMR időskálájához képest gyors. Más izotópok kémiai eltolódása, például a 31P-é is mérhető NMR-rel.
Mikroállandók
[szerkesztés]
Egyes bázisok, mint például a spermin, több helyen is protonálódhatnak. Ebben a példában az első proton a láncvégi –NH2 vagy a két belső –NH– csoporthoz kapcsolódhat. Az egyik vagy másik nitrogénen protonált spermin disszociációjának pKa értékei a mikroállandók egyik példája. A mikroállandók közvetlenül nem határozhatók meg pH, abszorbancia, fluoreszcencia vagy NMR méréssel. A protonálódás helye ugyanakkor a biológiai funkció szempontjából nagyon fontos, ezért a mikroállandók meghatározására matematikai módszereket fejlesztettek ki.[43]
Alkalmazások és jelentősége
[szerkesztés]A pKa értékének ismerete fontos a sav-bázis egyensúlyokat tartalmazó oldatok kvantitatív leírásához. A biokémiában számos esetben alkalmazzák, például a fehérjék és aminosavak oldalláncának pKa értékei különösen fontos szerepet játszanak az enzimek aktivitásában és a fehérjék stabilitásában.[44] A fehérjék pKa-ját nem lehet mindig közvetlenül mérni, de elméleti módszerekkel ki lehet számítani őket. A biokémiai reakciók vizsgálatában széles körben használnak pufferoldatokat, hogy a fiziológiás vagy ahhoz közeli pH-n tartsák az oldatokat;[45] ezeknek az oldatoknak az összetétele a komponensek pKa értékeinek ismeretén alapul. A fontos pufferek közé tartozik a MOPS, ennek oldata 7,2-es pH-jú, valamint a tricin, melyet a gélelektroforézisben alkalmaznak.[46][47] A pufferhatás alapvető része a sav-bázis fiziológiának, beleértve a sav-bázis homeosztázist is,[48] és kulcsfontosságú az olyan zavarok megértésében, mint a sav-bázis kiegyensúlyozatlanság.[49][50][51] Egy molekula izoelektromos pontja a pK értékek függvénye, így különböző molekulák különböző izoelektromos ponttal rendelkeznek. Ezen a jelenségen alapul az izoelektromos fókuszálás nevű módszer,[52] melyet fehérjék kétdimenziós gélelektroforézises elválasztására használnak.
A pufferoldatok az analitikai kémiában is kulcsszerepet játszanak. Ha egy oldat pH-ját egy adott értéken kell tartani, akkor pufferoldatot alkalmaznak. A vizes oldatokkal szemben a pufferoldat pH-ja viszonylag érzéketlen a kis mennyiségű erős sav vagy lúg hozzáadásával szemben. Egy egyszerű oldat pufferkapacitása[53] akkor a legnagyobb, amikor pH = pKa. A sav-bázis extrakció során egy vegyületnek a szerves fázisba, például éterbe történő extrahálásának hatásfoka optimálható, ha a vizes fázis pH-ját valamilyen pufferrel beállítjuk a megfelelő értékre. Az optimális pH-n az elektromosan semleges részecske koncentrációja maximális, és jobban oldódik a kis dielektromos állandójú szerves oldószerekben, mint vízben. Ezt az eljárást gyenge savak és bázisok tisztítására alkalmazzák.[54]
A pH-indikátor olyan gyenge sav vagy bázis, amelynek a színe egy átmeneti pH-tartományban (az átcsapási tartományban) megváltozik. Ez a tartomány körülbelül pKa ± 1. Az univerzális indikátorok olyan indikátorkeverékek, melyek szomszédos pKa értékei körülbelül kettővel különböznek, így átcsapási tartományaik éppen csak átfednek.
A farmakológiában egy vegyület ionizációja megváltoztatja annak fizikai és makroszkopikus tulajdonságait, mint például az oldhatóságát vagy liofilicitását (log p). Egy vegyület ionizációja például növeli annak vízoldhatóságát, de csökkenti a liofilicitását. A gyógyszerfejlesztés során ezt használják fel a vegyület vérbeli koncentrációjának növelésére: az ionizációra képes csoport pKa értékét a megfelelő értékre módosítják.[55]
A pKa értékének ismerete fontos a koordinációs komplexek megértéséhez, melyek egy Mm+ fémion, mint Lewis-sav és L ligandum, mint Lewis-bázis közötti kölcsönhatás során keletkeznek. A ligandum azonban protonálódhat, ezért a komplexek keletkezése vizes oldatban az alábbi reakcióval írható le:
- [M(H2O)n]m+ +LH ⇌ [M(H2O)n−1L](m−1)+ + H3O+
Ahhoz, hogy meghatározzuk ennek a reakciónak – amelyben a ligandum lead egy protont – az egyensúlyi állandóját, ismerni kell a protonált ligandum Ka-ját. A gyakorlatban a ligandum többértékű is lehet, az EDTA4− például négy protont vehet fel, ilyen esetben az összes pKa értéket ismerni kell. A fémion ráadásul hidrolizálhat is, azaz gyenge savként viselkedhet, ezért a hidrolízis pK értékének is ismertnek kell lennie.[56]
A savakkal vagy bázisokkal kapcsolatos veszélyek értékeléséhez is szükség lehet a pKa értékek ismeretére.[57] A hidrogén-cianid például erősen mérgező gáz, mert a cianidion gátolja a vastartalmú citokróm c oxidáz enzimet. A hidrogén-cianid vizes oldatban gyenge sav, pKa-ja körülbelül 9. Erősen lúgos oldatban, mintegy 11-es pH fölött ezért „teljesen disszociált” állapotban van, így a hidrogén-cianid által okozott veszély jóval kisebb. A savas oldatok ellenben nagyon veszélyesek, mivel az összes cianid protonált, sav formában található. Cianid lenyelése – a citokróm c oxidázzal való reakció miatt – a pH-tól függetlenül potenciálisan halálos.
A környezettudományokban a sav-bázis egyensúlyok fontosak a tavak[58] és folyók szempontjából,[59][60] a huminsavak például fontos összetevői a természetes vizeknek. Egy másik példa a kémiai oceanográfia területéről:[61] a vas(III) különböző szalinitású tengervízben való oldhatóságának meghatározásához a vas-hidroxid oldhatósági szorzatával együtt meg kellett határozni a vas(III) hidrolízis termékek (Fe(OH)2+, Fe(OH)+2 és Fe(OH)3) képződésének pKa értékét is.[62]
Néhány anyag pKa értéke
[szerkesztés]Többféle módszer is létezik arra, hogy meghatározzák a vegyületek pKa-ját, ezért a különböző források között van némi eltérés.
A helyesen meghatározott értékek között a különbség jellemzően nem haladja meg a 0,1 egységet. Az alábbi adatok 25 °C-os vízre vonatkoznak.[3][63]
További értékek találhatók fentebb a termodinamika szakaszban.
| Kémiai név | Egyensúly | pKa |
|---|---|---|
| B = Adenin | BH2+2 ⇌ BH+ + H+ | 4,17 |
| BH+ ⇌ B + H+ | 9,65 | |
| H3A = Arzénsav | H3A ⇌ H2A− + H+ | 2,22 |
| H2A− ⇌ HA2− + H+ | 6,98 | |
| HA2− ⇌ A3− + H+ | 11,53 | |
| HA = Benzoesav | HA ⇌ H+ + A− | 4,204 |
| HA = Butánsav | HA ⇌ H+ + A− | 4,82 |
| H2A = Krómsav | H2A ⇌ HA− + H+ | 0,98 |
| HA− ⇌ A2− + H+ | 6,5 | |
| B = Kodein | BH+ ⇌ B + H+ | 8,17 |
| HA = Krezol | HA ⇌ H+ + A− | 10,29 |
| HA = Hangyasav | HA ⇌ H+ + A− | 3,751 |
| HA = Hidrogén-fluorid | HA ⇌ H+ + A− | 3,17 |
| HA = Hidrogén-cianid | HA ⇌ H+ + A− | 9,21 |
| HA = Hidrogén-szelenid | HA ⇌ H+ + A− | 3,89 |
| HA = Hidrogén-peroxid (90%) | HA ⇌ H+ + A− | 11,7 |
| HA = Tejsav | HA ⇌ H+ + A− | 3,86 |
| HA = Propánsav | HA ⇌ H+ + A− | 4,87 |
| HA = Fenol | HA ⇌ H+ + A− | 9,99 |
| H2A = L-(+)-aszkorbinsav | H2A ⇌ HA− + H+ | 4,17 |
| HA− ⇌ A2− + H+ | 11,57 |
Fordítás
[szerkesztés]- Ez a szócikk részben vagy egészben a Acid dissociation constant című angol Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.
Jegyzetek
[szerkesztés]- ↑ Miessler, G.. Inorganic Chemistry, 2nd, Prentice Hall (1991). ISBN 0134656598 Chapter 6: Acid-Base and Donor-Acceptor Chemistry
- ↑ Bell, R.P.. The Proton in Chemistry, 2nd, London: Chapman & Hall (1973) Számos szerves Brønsted savat tárgyal.
- ↑ a b c Shriver, D.F, Atkins, P.W.. Inorganic Chemistry, 3rd, Oxford: Oxford University Press (1999). ISBN 0198503318 Chapter 5: Acids and Bases
- ↑ Housecroft, C.E., Sharpe, A.G.. Inorganic Chemistry, 3rd, Prentice Hall (2008). ISBN 0131755536 Chapter 6: Acids, Bases and Ions in Aqueous Solution
- ↑ Headrick, J.M., Diken, E.G.; Walters, R. S.; Hammer, N. I.; Christie, R.A. ; Cui, J.; Myshakin, E.M.; Duncan, M.A.; Johnson, M.A.; Jordan, K.D. (2005). „Spectral Signatures of Hydrated Proton Vibrations in Water Clusters”. Science 308, 1765–69. o. DOI:10.1126/science.1113094.
- ↑ Smiechowski, M., Stangret, J. (2006). „Proton hydration in aqueous solution: Fourier transform infrared studies of HDO spectra”. J. Chem. Phys. 125, 204508–204522. o. DOI:10.1063/1.2374891.
- ↑ Burgess, J.. Metal Ions in Solution. Ellis Horwood (1978). ISBN 0853120277 Section 9.1 "Acidity of Solvated Cations" lists many pKa values.
- ↑ a b Rossotti, F.J.C., Rossotti, H.. The Determination of Stability Constants. McGraw–Hill (1961) Chapter 2: Activity and Concentration Quotients
- ↑ a b Popov, K., Ronkkomaki, H.; Lajunen, L.H.J. (2006). „Guidelines for NMR Measurements for Determination of High and Low pKa Values” (PDF). Pure Appl. Chem. 78 (3), 663–675. o. [2016. március 3-i dátummal az eredetiből archiválva]. DOI:10.1351/pac200678030663. (Hozzáférés: 2009. augusztus 3.)
- ↑ https://www.tankonyvtar.hu/hu/tartalom/tamop412A/2011_0025_vegy_3/ch01.html
- ↑ Project: Ionic Strength Corrections for Stability Constants. International Union of Pure and Applied Chemistry. [2008. október 29-i dátummal az eredetiből archiválva]. (Hozzáférés: 2008. november 23.)
- ↑ Dasent, W.E.. Inorganic Energetics: An Introduction. Cambridge University Press (1982). ISBN 0521284066 Chapter 5
- ↑ Brown, T.E., Lemay, H.E.; Bursten,B.E.; Murphy, C.; Woodward, P.. Chemistry: The Central Science, 11th, New York: Prentice-Hall, 689. o. (2008). ISBN 0136006175
- ↑ a b Greenwood, N.N.. Az elemek kémiája, 1., Budapest: Nemzeti Tankönyvkiadó, 67. o. (1999). ISBN 963-18-9144-5
- ↑ Lide, D.R.. CRC Handbook of Chemistry and Physics, Student Edition, 84th, CRC Press (2004). ISBN 0849305977 Section D–152
- ↑ Atkins, P.W., de Paula, J.. Fizikai kémia. Nemzeti Tankönyvkiadó (1998). ISBN 963-18-9163-1 9.4 fejezet: A hőmérséklet hatása az egyensúlyra
- ↑ a b c d Loudon, G. Marc (2005), Organic Chemistry (4th ed.), New York: Oxford University Press, pp. 317–318, ISBN 0-19-511999-1
- ↑ March, J., Smith, M.. Advanced Organic Chemistry, 6th, New York: John Wiley & Sons (2007). ISBN 978-0-471-72091-1 Chapter 8: Acids and Bases
- ↑ Kütt, A., Movchun, V.; Rodima, T,; Dansauer, T.; Rusanov, E.B. ; Leito, I.; Kaljurand, I.; Koppel, J.; Pihl, V.; Koppel, I.; Ovsjannikov, G.; Toom, L.; Mishima, M.; Medebielle, M.; Lork, E.; Röschenthaler, G-V.; Koppel, I.A.; Kolomeitsev, A.A. (2008). „Pentakis(trifluoromethyl)phenyl, a Sterically Crowded and Electron-withdrawing Group: Synthesis and Acidity of Pentakis(trifluoromethyl)benzene, -toluene, -phenol, and -aniline”. J. Org. Chem. 73 (7), 2607–2620. o. DOI:10.1021/jo702513w.
- ↑ a b Kütt, A., Leito, I.; Kaljurand, I.; Sooväli, L.; Vlasov, V.M.; Yagupolskii, L.M.; Koppel, I.A. (2006). „A Comprehensive Self-Consistent Spectrophotometric Acidity Scale of Neutral Brønsted Acids in Acetonitrile”. J. Org. Chem. 71 (7), 2829–2838. o. DOI:10.1021/jo060031y.
- ↑ Kaljurand, I., Kütt, A.; Sooväli, L.; Rodima, T.; Mäemets, V. Leito, I; Koppel, I.A. (2005). „Extension of the Self-Consistent Spectrophotometric Basicity Scale in Acetonitrile to a Full Span of 28 pKa Units: Unification of Different Basicity Scales”. J. Org. Chem. 70 (3), 1019–1028. o. DOI:10.1021/jo048252w.
- ↑ Bordwell pKa Table (Acidity in DMSO). (Hozzáférés: 2008. november 2.)
- ↑ Housecroft, C.E., Sharpe, A.G.. Inorganic Chemistry, 3rd, Prentice Hall (2008). ISBN 0131755536 Chapter 8: Non-Aqueous Media
- ↑ Rochester, C.H.. Acidity Functions. Academic Press (1970). ISBN 0125908504
- ↑ Olah, G.A, Prakash, S; Sommer, J. Superacids. New York: Wiley Interscience (1985). ISBN 0471884693
- ↑ Coetzee, J.F., Padmanabhan, G.R. (1965). „Proton Acceptor Power and Homoconjugation of Mono- and Diamines”. J. Amer. Chem. Soc. 87, 5005–5010. o. DOI:10.1021/ja00950a006.
- ↑ Pine, S.H., Hendrickson, J.B.; Cram, D.J.; Hammond, G.S. (1980). „Organic chemistry”, 203. o, Kiadó: McGraw–Hill.
- ↑ Box, K.J., Völgyi, G. Ruiz, R. Comer, J.E. Takács-Novák, K., Bosch, E. Ràfols, C. Rosés, M. (2007). „Physicochemical Properties of a New Multicomponent Cosolvent System for the pKa Determination of Poorly Soluble Pharmaceutical Compounds”. Helv. Chim. Acta 90 (8), 1538–1553. o. DOI:10.1002/hlca.200790161.
- ↑ Pauling, L.. The nature of the chemical bond and the structure of molecules and crystals; an introduction to modern structural chemistry, 3rd, Ithaca (NY): Cornell University Press, 277. o. (1960)
- ↑ Pine, S.H., Hendrickson, J.B.; Cram, D.J.; Hammond, G.S.. Organic Chemistry. McGraw–Hill (1980). ISBN 0070501157 Section 13-3: Quantitative Correlations of Substituent Effects (Part B) – The Hammett Equation
- ↑ Hammett, L.P. (1937). „The Effect of Structure upon the Reactions of Organic Compounds. Benzene Derivatives”. J. Amer. Chem. Soc. 59 (1), 96–103. o. DOI:10.1021/ja01280a022.
- ↑ Hansch, C., Leo, A.; Taft, R. W. (1991). „A Survey of Hammett Substituent Constants and Resonance and Field Parameters”. Chem. Rev. 91 (2), 165–195. o. DOI:10.1021/cr00002a004.
- ↑ Shorter, J (1997). „Compilation and critical evaluation of structure-reactivity parameters and equations: Part 2. Extension of the Hammett σ scale through data for the ionization of substituted benzoic acids in aqueous solvents at 25 C (Technical Report)” 69 (12), 2497–2510. o. DOI:10.1351/pac199769122497.
- ↑ Pine, S.H., Hendrickson, J.B.; Cram, D.J.; Hammond, G.S.. Organic chemistry. McGraw–Hill (1980). ISBN 0070501157 Section 6-2: Structural Effects on Acidity and Basicity
- ↑ Alder, R.W., Bowman, P.S.; Steele, W.R.S.; Winterman, D.R. (1968). „The Remarkable Basicity of 1,8-bis(dimethylamino)naphthalene”. Chem. Commun., 723–724. o, 723. o. DOI:10.1039/C19680000723.
- ↑ Alder, R.W. (1989). „Strain Effects on Amine Basicities”. Chem. Rev. 89, 1215–1223. o. DOI:10.1021/cr00095a015.
- ↑ a b Goldberg, R., Kishore, N.; Lennen, R. (2002). „Thermodynamic Quantities for the Ionization Reactions of Buffers” (PDF). J. Phys. Chem. Ref. Data 31, 231–370. o. [2009. október 13-i dátummal az eredetiből archiválva]. DOI:10.1063/1.1416902. (Hozzáférés: 2009. augusztus 3.)
- ↑ Martell, A.E., Motekaitis, R.J.. Determination and Use of Stability Constants. Wiley (1992). ISBN 0471188174 Chapter 4: Experimental Procedure for Potentiometric pH Measurement of Metal Complex Equilibria
- ↑ Leggett, D.J.. Computational Methods for the Determination of Formation Constants. Plenum (1985). ISBN 0306419572
- ↑ Allen, R.I., Box,K.J.; Comer, J.E.A.; Peake, C.; Tam, K.Y. (1998). „Multiwavelength Spectrophotometric Determination of Acid Dissociation Constants of Ionizable Drugs”. J. Pharm. Biomed. Anal. 17 (4–5), 699–641. o. DOI:10.1016/S0731-7085(98)00010-7.
- ↑ Szakács, Z., Hägele, G. (2004). „Accurate Determination of Low pK Values by 1H NMR Titration”. Talanta 62, 819–825. o. DOI:10.1016/j.talanta.2003.10.007.
- ↑ Box, K.J., Donkor, R.E. Jupp, P.A. Leader, I.P. Trew, D.F. Turner, C.H. (2008). „The Chemistry of Multi-Protic Drugs Part 1: A Potentiometric, Multi-Vavelength UV and NMR pH Titrimetric Study of the Micro-Speciation of SKI-606”. J. Pharm. Biomed. Anal. 47 (2), 303–311. o. DOI:10.1016/j.jpba.2008.01.015.
- ↑ Frassineti, C., Alderighi, L; Gans, P; Sabatini, A; Vacca, A; Ghelli, S. (2003). „Determination of Protonation Constants of Some Fluorinated Polyamines by Means of 13C NMR Data Processed by the New Computer Program HypNMR2000. Protonation Sequence in Polyamines.”. Anal. Bioanal. Chem. 376, 1041–1052. o. DOI:10.1007/s00216-003-2020-0.
- ↑ Onufriev, A., Case, D.A; Ullmann G.M. (2001). „A Novel View of pH Titration in Biomolecules”. Biochemistry 40, 3413–3419. o. DOI:10.1021/bi002740q.
- ↑ Good, N.E., Winget, G.D.; Winter, W.; Connolly, T.N.; Izawa, S.; Singh, R.M.M. (1966). „Hydrogen Ion Buffers for Biological Research”. Biochemistry 5 (2), 467–477. o. DOI:10.1021/bi00866a011.
- ↑ Dunn, M.J.. Gel Electrophoresis: Proteins. Bios Scientific Publishers (1993). ISBN 187274821X
- ↑ Martin, R.. Gel Electrophoresis: Nucleic Acids. Bios Scientific Publishers (1996). ISBN 1872748287
- ↑ Brenner, B.M. (Editor), Stein, J.H. (Editor). Acid–Base and Potassium Homeostasis. Churchill Livingstone (1979). ISBN 0443080178
- ↑ Scorpio, R.. Fundamentals of Acids, Bases, Buffers & Their Application to Biochemical Systems. Kendall/Hunt Pub. Co. (2000). ISBN 0787273740
- ↑ Beynon, R.J., Easterby, J.S.. Buffer Solutions: The Basics. Oxford: Oxford University Press (1996). ISBN 0199634424
- ↑ Perrin, D.D., Dempsey, B.. Buffers for pH and Metal Ion Control. London: Chapman & Hall (1974). ISBN 0412117002
- ↑ Garfin, D.(Editor), Ahuja, S. (Editor). Handbook of Isoelectric Focusing and Proteomics. Elsevier (2005). ISBN 0120887525U
- ↑ Hulanicki, A.. Reactions of Acids and Bases in Analytical Chemistry, Masson, M.R. (translation editor), Horwood (1987). ISBN 0853123306
- ↑ Eyal, A.M (1997). „Acid Extraction by Acid–Base-Coupled Extractants”. Ion Exchange and Solvent Extraction: A Series of Advances 13, 31–94. o.
- ↑ Avdeef, A.. Absorption and Drug Development: Solubility, Permeability, and Charge State. New York: Wiley (2003). ISBN 0471423653
- ↑ Beck, M.T., Nagypál, I.. Chemistry of Complex Equilibria. Horwood (1990). ISBN 0853121435
- ↑ van Leeuwen, C.J., Hermens, L. M.. Risk Assessment of Chemicals: An Introduction. Springer, 254–255. o. (1995). ISBN 0792337409
- ↑ Skoog, D.A, West, D.M.; Holler, J.F.; Crouch, S.R.. Fundamentals of Analytical Chemistry, 8th, Thomson Brooks/Cole (2004). ISBN 0-03-035523-0 Chapter 9-6: Acid Rain and the Buffer Capacity of Lakes
- ↑ Stumm, W., Morgan, J.J.. Water Chemistry. New York: Wiley (1996). ISBN 0471051969
- ↑ Snoeyink, V.L., Jenkins, D.. Aquatic Chemistry: Chemical Equilibria and Rates in Natural Waters. New York: Wiley (1980). ISBN 0471511854
- ↑ Millero, F.J.. Chemical Oceanography, 3rd, London: Taylor and Francis (2006). ISBN 0849322804
- ↑ Millero, F.J., Liu, X. (2002). „The Solubility of Iron in Seawater”. Marine chemistry 77, 43–54. o. DOI:10.1016/S0304-4203(01)00074-3.
- ↑ Speight, J.G.. Lange's Handbook of Chemistry, 18th, McGraw–Hill (2005). ISBN 0071432205 Chapter 8

![{\displaystyle K_{\mathrm {a} }=\mathrm {\frac {[A^{-}][H^{+}]}{[HA]}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/4df1424aa532585fc7ad6dd660a596705ee31a2b)


![{\displaystyle K^{\ominus }=\mathrm {{\frac {[A^{-}][H_{3}O^{+}]}{[HA][H_{2}O]}}\cdot {\frac {\gamma _{A^{-}}\gamma _{H_{3}O^{+}}}{\gamma _{HA}\gamma _{H_{2}O}}}=\mathrm {\frac {[A^{-}][H_{3}O^{+}]}{[HA][H_{2}O]}} \cdot \Gamma } }](https://wikimedia.org/api/rest_v1/media/math/render/svg/50bc1984363b2e1c656497ef5eee5386f2dd997e)
![{\displaystyle \mathrm {pH} =\mathrm {p} K_{\mathrm {a} }-\log \mathrm {\frac {[AH]}{[A^{-}]}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/5aeae35bc89259be2d76c855efb0f2abeb595aae)
![{\displaystyle K_{\mathrm {a} }=\mathrm {\frac {[H_{3}O^{+}][OH^{-}]}{[H_{2}O]^{2}}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0fd2af6a4e208433b23af32cd7afa504c549f0e)
![{\displaystyle K_{\mathrm {w} }=[\mathrm {H_{3}O} ^{+}][\mathrm {OH} ^{-}]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b28e22a7001351bdc196d0c1d2e7ea94f3b2842f)
![{\displaystyle K_{\mathrm {b} }=\mathrm {\frac {[HB^{+}][OH^{-}]}{[B]}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e8602a5fa0751164332991a802fe0f0a9226ba2)
![{\displaystyle \mathrm {[OH^{-}]} ={\frac {K_{\mathrm {w} }}{\mathrm {[H^{+}]} }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab7f583da9f8b50145990ffa4342919930edfa16)
![{\displaystyle K_{\mathrm {b} }={\frac {[\mathrm {HB^{+}} ]K_{\mathrm {w} }}{\mathrm {[B][H^{+}]} }}={\frac {K_{\mathrm {w} }}{K_{\mathrm {a} }}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55e99b9289faff1c69f7cc5b289e461e363515a5)
