Riemann-sejtés
A Riemann-sejtés, amelyet először Bernhard Riemann fogalmazott meg 1859-ben, egyetlen számelméleti tárgyú dolgozatában, a Riemann-féle zéta-függvény zérushelyeinek eloszlásával foglalkozik (és így a prímszámok lehető legegyenletesebb eloszlását állítja). Sokan (így például Erdős Pál is) az egész matematika legfontosabb problémájának, koronagyémántjának tartják. Egyike a Hilbert-problémáknak, és az egymillió dollárt érő millenniumi problémáknak is. A legtöbb matematikus igaznak tartja, bár például John Edensor Littlewood és Atle Selberg hangoztatott kétségeket.
A Riemann-féle zéta-függvény ζ(s) egyváltozós, komplex számokon értelmezett függvény, értelmezési tartománya a teljes komplex számsík, s = 1 kivételével. Ha s>1 valós szám, akkor a konvergens
sor állítja elő, ez még akkor is konvergens, ha s komplex, de valós része 1-nél nagyobb. Így például az ismert Euler-féle formula miatt ζ(2)=π²/6. Ha s valós része nem 1-nél nagyobb, akkor analitikus folytatással kapjuk a függvény értékeit.
Vannak úgynevezett triviális gyökhelyei a negatív páros számokban, azaz az s = −2, s = −4, s = −6, … értékeknél. A Riemann-sejtés a nem triviális esetekkel foglalkozik, és kimondja:
A Riemann-féle ζ-függvény minden nem triviális gyökének a valós része 1/2.
Tehát a nemtriviális gyökök az 1/2 + it alakú számokból álló úgynevezett kritikus egyenesen vannak, ahol t valós szám és i a képzetes egység.
Ekvivalens állítások
[szerkesztés]Számos, elsőre egyszerűnek tűnő állítás valójában ekvivalens a Riemann-hipotézissel, például:
1. minden természetes számra teljesül
ahol az első szám legkisebb közös többszörösét jelöli.
2. Robin tétele: Guy Robin 1984-ben bizonyította, hogy a következő állítás:
ahol σ(n) az osztóösszeg-függvény, és γ az Euler–Mascheroni-állandó; szintén ekvivalens a Riemann-sejtéssel.[1]
3. Lagarias tétele: 2002-ben Jeffrey Lagarias megmutatta, hogy a Riemann-sejtés ekvivalens a σ(n) osztóösszeg-függvényre vonatkozó következő felső becsléssel:
minden n természetes számra, ahol Hn a harmonikus sorozat ().[2]
A Riemann-féle zéta-függvény
[szerkesztés]
A Riemann-féle zéta-függvény egy komplex értékű függvény. Definíciója a komplex sík tartományán a következő:
ahol s a komplex szám. Ezt a függvényt kiterjesztik a komplex síkra, kivéve az egyet, ahol pólusa van.
Fontos tulajdonsága, hogy kapcsolódik a prímszámokhoz, továbbá összekapcsolja a komplex függvénytant a számelmélettel, és rá alapul a Riemann-sejtés. Mindezek miatt a sejtésnek számos következménye van a számelmélet különböző területein. Leonhard Euler 1748-ban ezzel az összefüggéssel mutatta meg a kapcsolatot:
ahol a végtelen szorzat befutja a prímszámokat. Ez az összefüggés a számelmélet alaptételének és a mértani sor összegképletének közvetlen következménye.
Ezzel a képlettel a Riemann-féle zéta-függvény a teljes komplex síkra kiterjeszthető, kivéve az egyszeres pólust, tehát meromorf függvényt kapunk.
- ,
ahol a teljes gammafüggvény, és a Bernoulli-számok. Az első néhány Bernoulli-szám:
Jelentősége
[szerkesztés]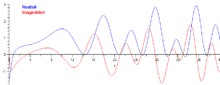
Kapcsolat a prímszámokkal
[szerkesztés]Már Riemann is felismerte a zéta-függvény és a prímszámok közötti kapcsolatot. Cikkében analitikus kifejezést keresett a prímszámláló függvényre. A kapcsolathoz a következő képletből indult ki:
Ennek logaritmusát véve:
Végül az
integrállal sikerült Riemann-nak a zéta-függvény logaritmusát analitikusan kifejeznie. Ehhez
ami minden x-nél kisebb prímhatványra összegzi az -t. Például,
Ez egy lépcsős függvény. Így integrálképlete:
A Fourier-analízis mestereként Riemann inverz Mellin-transzformációval a következőre jutott:
ahol c > 1. A továbbiakban a kszí-függvénnyel kezdett el foglalkozni:
Innen már egyszerű volt a második nem triviális kifejezést megkapnia -re:
A továbbiakban ezt behelyettesítette helyére:
Ennek nehézkes kiértékelése ellenére sikerült a következőre jutnia:
ahol az integrállogaritmus. Ezután egy Möbius-inverzióval összekapcsolta a és a függvényeket:
ami egy mélyebb összefüggést ad a prímszámok és a zéta-függvény gyökei között.
Megjegyzés: Numerikus számítás esetén a Riemann-képletben az összegben -t -szel kell helyettesíteni, ahol a komplex integrálexponenciális függvény, mivel kiértékelésekor a logaritmus főágára nem biztos, hogy teljesül , így hamis eredményre jutnánk.
Következmények
[szerkesztés]Ha a Riemann-sejtés igaz, akkor a prímszámok számának becslése pontosítható: (Helge von Koch 1901):[3]
Sőt, Koch eredménye ekvivalens a Riemann-sejtéssel. Az előbbi összefüggés egy másik alakja:
egy konstans erejéig, és ennek egy szigorú gyengítése (ami nem ekvivalens):
tetszőleges -ra.
Az analitikus számelméletben sok eredmény, sőt a kriptográfiában is fontos gyors prímtesztek is csak a Riemann-sejtést feltéve vannak bizonyítva. Michael Berry fizikus szerint a zéta-függvény komplex gyökeiben kódoltan megjelennek a prímszámok eloszlásának fluktuációi az aszimptotikus logaritmikus eloszlás körül. A pontos eloszlás ismeretében pontosabb kijelentések tehetők arról, hogy egy tartományban mennyi prímszám van.
A sejtés egy különben kaotikusan viselkedő függvény egy szimmetriatulajdonságáról szól. A zéta-függvény kaotikusságát mutatja, hogy minden, az azonosan nullától különböző analitikus függvényt egy 1/4 sugarú körben approximál. Ez a szimmetria maga valószínűleg egy alapvető elméletet rejt, ahogy például a nagy Fermat-tétel is az elliptikus görbék moduláris függvényekkel való paraméterezését, amit a Langlands-program vizsgált.
Története
[szerkesztés]Eredete
[szerkesztés]A sejtést Bernhard Riemann vetette fel, amikor a zéta- és a gammafüggvény szorzatát tanulmányozta. Ez írható az
- ,
alakban. Erről Riemann kiderítette, hogy invariáns arra, hogy felcseréljük az -t -sel. Más szavakkal, megfelel az
függvényegyenletnek. Az helyettesítéssel nyerte a következőt minden -re:
Ennek a tükrözésnek a tengelye az 1/2 valós részű komplex számok egyenese, ami pontonként fix. Riemann ugyan valós gyökökről írt, de ezzel arra gondolt, hogy az kritikus sávban a
egyenlet csak valós t-kre oldható meg.
Gyökmentes tartomány
[szerkesztés]Az analitikus számelméletben a komplex számokat általában s=σ+ti alakban szokták felírni, tehát σ a valós rész, t a képzetes rész. A sejtés tehát az, hogy a 0≤σ≤1 sávba eső gyökökre σ=½ teljesül. Először Jacques Hadamard és Charles Jean de la Vallée-Poussin igazolta, hogy nincs a σ=1 egyenesen gyök. Ebből már következik a prímszámtétel és mint utóbb kiderült, ekvivalens is vele. De la Vallée Poussin azt is igazolta, hogy ha s=σ+ti, akkor
teljesül.
Ezt Littlewood javította meg 1922-ben:
A következő eredményt Korobov és Vinogradov adta 1958-ban:
minden ε>0-ra.
A legjobb eredmény szerint[4] ha |t| ≥ 3, akkor
Általánosítási kísérlet
[szerkesztés]Pólya György 1919-ben felállította azt az erősebb sejtést, hogy tetszőleges x természetes számra azon számok száma, amiknek páratlan sok prímtényezője van (összesen), legalább annyi, mint amennyinek páros. Ezt C. Brian Haselgrove 1958-ban megcáfolta, nem igaz például x=906 180 359-re.
Hamis riasztások
[szerkesztés]- 1885-ben Stieltjes rövid jegyzetet publikált a párizsi akadémia Comptes Rendusjében és egy Hermite-nek írt levelében megerősítette, hogy bebizonyította a Mertens-sejtést, ami erősebb, mint a Riemann-sejtés. Bizonyítást azonban haláláig nem publikált, és jegyzetei között sem találták nyomát.
- A kiváló matematikus, Johan Jensen 1899-es cikkében megemlítette, hogy bebizonyította a Riemann-sejtést.
- 1943-ban Hans Rademacher az utolsó pillanatban vonta vissza cikkét a Transactions of the American Mathematical Society c. folyóiratból, miután Siegel megtalálta a hibát.
- 1961-ben az odesszai egyetem folyóiratában publikálta hibás bizonyítását N. I. Gavrilov. Később külön brosúrában majd könyvben is megjelentette, az ogyesszai illetve a lembergi egyetem kiadásában.
- 2004. június 8-án a Purdue Egyetem sajtóközleményében jelentette be Louis de Branges, hogy fáradozásai sikerrel jártak: bizonyítását feltette a világhálóra. Sajnos ebben egy olyan megközelítést használt, amelynek a cáfolatát már 1998-ban bemutatták.[5] De Branges ezen kívül még számos hibás bizonyítást adott az invariáns alterek problémájára, a mérhető számosságok nemlétezésére és a Riemann-sejtésre. A Bieberbach-problémára adott 1984-es bizonyítása azonban utóbb helyesnek (pontosabban javíthatónak) bizonyult.
- 2007-ben tette közzé a Riemann-sejtés cáfolatát Tribikram Pati. Bizonyítását hibásnak mutatta ki például Bernhard Johann Krötz.[6]
Általánosításai
[szerkesztés]Az általánosított Riemann-sejtésen rendszerint a következőt értik:[7]
Tetszőleges Dirichlet-karakterhez tartozó Dirichlet-sor analitikus folytatásának
a kritikus sávban az összes gyökére teljesül, hogy Ennek a Riemann-sejtés egy speciális esete. Andrew Granville belátta, hogy ez az általánosított Riemann-sejtés ekvivalens a Goldbach-sejtéssel.[7]
Kapcsolatai más sejtésekkel
[szerkesztés]Az analitikus számelméletben más sejtések is kapcsolatba hozhatók a Riemann-sejtéssel.
A Merstens-sejtés azt állítja, hogy minden -re. Itt a Möbius-függvény és a Mertens-függvény. A Riemann-sejtésnél szigorúbb sejtést 1985-ben megcáfolták.[8]
Arnaud Denjoy valószínűségi értelmezést adott a Riemann-sejtésnek.[9] Legyen egy véletlen sorozat az (1, -1) elemekből egyenlő valószínűséggel. Ekkor minden -ra
ami azt jelenti, hogy a nullától való távolság legfeljebb olyan gyorsan nő, mint . Ha itt a Möbius-függvény, akkor a Riemann-hipotézis ekvivalens azzal, hogy ez az aszimptotikus növekedés az összegre is érvényes.(Littlewood 1912)[10] Littlewood továbbá azt is belátta, hogy a Riemann-sejtés a következővel is ekvivalens: Minden esetén a tart a nullához, ha x tart a végtelenhez. A Riemann-hipotézis értelmezhető úgy, hogy a Möbius-függvény eloszlása véletlenszerű.
Továbbá következik egy korlát is a prímszámtétel hibájának növekedésére. Koch eredménye azonban ekvivalens a Riemann-hipotézissel.[11]
A következőből következik a Riemann-hipotézis:
A Lindelöf-sejtés a zéta-függvény növekedéséről a kritikus egyenes mentén gyengébb a Riemann-sejtésnél, de nincs bizonyítva.
Riesz Marcell 1916-ban megmutatta az ekvivalenciát a Riesz-függvény aszimptotikus viselkedésével kapcsolatos sejtéssel. Jerome Franel 1924-ben egy Farey-sorokról tett kijelentéssel kapcsolatban bizonyított ekvivalenciát. Ez azt állítja, hogy a (0,1) intervallum racionális számainak rendezése lineáris formába és a Farey-sorok sorrendje egy jóldefiniált matematikai értelemben annyira eltér, amennyire csak lehet.
Jeffrey Lagarias 1992-ben egy ekvivalens sejtést fogalmazott meg az elemi számelmélet eszközeivel.[12]
Bizonyítási ötletek a fizikából
[szerkesztés]A bizonyítás újabb ötletei a fizikából származnak. Már David Hilbertnek és Pólya Györgynek feltűnt, hogy a Riemann-sejtés következne abból, hogy ha a gyökök egy (1/2 + i T) operátor sajátértékei lennének, ahol T hermitikus, tehát minden sajátértéke valós, mint a kvantummechanika Hamilton-operátorainak. Az 1970-es években Hugh Montgomery beszélgetve Freeman Dysonnal arra jutott, hogy az egymást követő gyökök távolsága hasonló eloszlást mutat, mint a véletlen unitérmátrixok sajátértékei. Ezt Andrew Odlyzko numerikus számításokkal megerősítette. Az 1990-es években fizikusok is, mint Michael Berry keresték az ezeket megalapozó rendszert, a kvantumkáosz elméletének rendszerében. Ez további támogatást kapott a Riemann-féle zéta-függvény explicit képleteinek és a Selberg-nyomformuláinak analógiájától, ami egy Riemann-felületen értelmezett Laplace-Beltrami-operátor sajátértékeit hozza kapcsolatba a zárt geodetikus görbék hosszával, és a kvantumkáosz Gutzwiller-képletével. Ez összekapcsolja egy klasszikus kaotikus rendszer, mint kvantummechanikai rendszer sajátértékeket (energiákat) a klasszikus eset periodikus pályáival. Ezek a nyomformulák azonosságot fejeznek ki a gyökök, pályaperiódusok és sajátértékek között.
Az Alain Connes által 1996-ban megadott operátor gyorsan illeszkedik. Mindazonáltal nem tudta kizárni a kritikus egyenesen kívüli gyökök létét.[13]
Egy további, a fizikából származó ötlet a Jang-Li-gyökök, amelyek a statikus mechanika analitikus folytatásának állapotösszegei. Jang Csen-ning és Li Cseng-tao bizonyították Pólya György egy eredményéből, hogy bizonyos modellek esetén a gyökök egy körön, más modellekben egy egyenesen helyezkednek el. A gyökök helye a fázisátmenetek alatti viselkedést határozza meg, hasonlóan, mint a Riemann-féle zéta-függvény a prímek elhelyezkedését.
Ezek mögött a következő analógia rejlik: A prímszámok elemi részecskék, amelyek a szorzás által kölcsönhatásba lépnek egymással, és így építik fel az összetett számokat. Ezzel együtt mindegyiket az összeadás építi fel. A zéta-függvényben ez a két aspektus összekapcsolódik.
Freeman Dyson 2009-ben az egydimenziós kvázikristályokkal hozta kapcsolatba a sejtést.[14]
Jegyzetek
[szerkesztés]- ↑ Robin, G.: Grandes Valeurs de la fonction somme des diviseurs et hypothèse de Riemann. J. Math. Pures Appl. 63, 187-213, 1984. Robin cikke.
- ↑ Lagarias, J.: An Elementary Problem Equivalent to the Riemann Hypothesis[halott link]. Amer. Math. Monthly 109 (2002), 534--543.
- ↑ Helge von Koch: Sur la distribution des nombres premiers, Acta Mathematica, Band 24, 1901, S. 159–182
- ↑ Ford, K. Vinogradov's integral and bounds for the Riemann zeta function, Proc. London Math. Soc. (3) 85 (2002), pp. 565-633
- ↑ Matthew Watkins: proposed (dis)proofs of the Riemann Hypothesis
- ↑ Jason Dyer: Riemann Hypothesis disproof #296
- ↑ a b Granville: Refinements of Goldbach’s Conjecture
- ↑ A. M. Odlyzko, H. J. J. te Riele: Disproof of the Mertens conjecture. In: J. reine angew. Math., Band 357, 1985, S. 138–160, dtc.umn.edu
- ↑ Denjoy: L’Hypothése de Riemann sur la distribution des zéros de , reliée à la théorie des probabilités. In: Comptes Rendus Acad. Sc., Band 192, 1931, S. 656–658. Edwards: Riemanns Zeta Function, 1974, S. 268. Edwards kommentiert diese Interpretation so: though it is quite absurd when considered carefully, gives a fleeting glimmer of plausibility to the Riemann hypothesis.
- ↑ Littlewood: Quelques conséquences de l’hypothèse que la fonction n’a pas de zéros dans le demi-plan . In: Comptes Rendus, Band 154, 1912, S. 263–266. Edwards, loc. cit. S. 261.
- ↑ Edwards: Riemann’s Zeta function, Kapitel 5
- ↑ Lagarias: An elementary problem equivalent to the Riemann hypothesis. In: American Mathematical Monthly, Band 109, 2002, S. 534–543
- ↑ Connes: Trace formula in non commutative geometry and the zeros of the Riemann zeta function. 1998
- ↑ Dyson: Birds and Frogs. (PDF) Notices AMS 2009
Fordítás
[szerkesztés]- Ez a szócikk részben vagy egészben a Riemannsche Vermutung című német Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.
Források
[szerkesztés]- Professor Chris Caldwell: The Riemann Hypothesis. The Prime pages. The University of Tennessee at Martin, 1994–2007. [2004. október 10-i dátummal az eredetiből archiválva]. (Hozzáférés: 2004. október 16.)
- A Purdue egyetem sajtóközleménye
- M. Watkins oldala az állítólagos bizonyításokról Archiválva 2004. október 13-i dátummal a Wayback Machine-ben
- Marcus du Sautoy: Die Musik der Primzahlen. Auf den Spuren des größten Rätsels der Mathematik. München: dtv / C. H. Beck. 2003–2004. ISBN 3-423-34299-4 (a sejtés története)
- John Derbyshire: Prime obsession – Bernhard Riemann and the greatest unsolved problem in Mathematics. Washington: (kiadó nélkül). 2003. ISBN 0-309-08549-7
- Andrew Granville: Refinements of Goldbach’s Conjecture, and the generalized Riemann hypothesis. Poznań: Faculty of Mathematics and Computer Science of Adam Mickiewicz University. 2007. 159–173. o. = Functiones et Approximatio, Commentarii Mathematici, 37.
- Harold Edwards: Riemann’s Zeta Function. New York 1974, Dover 1991, ISBN 0-486-41740-9.
- Karl Sabbagh: Dr. Riemann’s Zeros. (hely nélkül): Atlantic. 2002.
- Edward Charles Titchmarsh: The Theory of the Riemann Zeta-Function. Átd. D. R. Heath-Brown. Oxford: (kiadó nélkül). 1987. ISBN 0-19-853369-1
- P. Borwein – S. Choi – B. Rooney – A. Weirathmueller: The Riemann hypothesis. A resource for the afficionado and virtuoso alike. New York: Canad. Math. Soc., Springer. 2008. = CMS Books in Mathematics, 27. ISBN 978-0-387-72125-5
- Julan Havil: Gamma – Eulers Konstante, Primzahlstrände und die Riemannsche Vermutung. (hely nélkül): Springer. 2007.
- Jürg Kramer: Die Riemannsche Vermutung. 2002. 90–95. o. = Elemente der Mathematik, 57.
- Dan Rockmore: Stalking the Riemann Hypothesis. (hely nélkül): Pantheon. 2005.
További információk
[szerkesztés]- John Derbyshire: Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. (hely nélkül): Joseph Henry Press. 2003. ISBN 0-309-08549-7 arch Hozzáférés: 2004. október 16.
- Karl Sabbagh: The Riemann Hypothesis. (hely nélkül): Farrar, Straus and Giroux. 2003. ISBN 0-374-25007-3
- Simonovits András: Válogatott fejezetek a matematika történetéből. (hely nélkül): Typotex. 2009. 133. o. ISBN 978-963-279-026-8



![{\displaystyle |\log([1,2,\dots ,n])-n|\leq {\sqrt {n}}\left(\log n\right)^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0681cd10a4f5bdb8066d20dddb97236abce87e58)
![{\displaystyle [1,2,\dots ,n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4683d2249d0d7087ae5c05e742cc479a5a6b843)







































































