Görbe vonalú affin Descartes-féle koordinátákA görbe vonalú koordináta-rendszerek az
E
n
{\displaystyle E^{n}}
diffeomorfak a Descartes-féle koordináta-rendszer koordinátavonalaival.[1]
A leggyakrabban alkalmazott görbe vonalú koordináta-rendszerek:
A szóban forgó feladattól függően egy megfelelően választott görbe vonalú koordináta-rendszerben a számítások egyszerűbbek lehetnek, mint a Descartes-koordináta-rendszerben. Például a sugaras szimmetriájú feladatokhoz célszerűbb lehet a gömbkoordináták választása.
A következők elsősorban a háromdimenziós térre vonatkoztathatók, ám nagy részük általánosítható más dimenziókra is.
A Descartes-koordináták transzformációja [ szerkesztés ] Egy
n
{\displaystyle n}
n
{\displaystyle n}
koordináta-rendszer erejéig határozza meg.
A Descartes-féle koordináta-rendszerben az
x
i
{\displaystyle x_{i}}
u
i
{\displaystyle u_{i}}
x
1
=
x
1
(
u
1
,
u
2
,
…
,
u
n
)
{\displaystyle x_{1}=x_{1}\left(u_{1},u_{2},\ldots ,u_{n}\right)\ }
x
2
=
x
2
(
u
1
,
u
2
,
…
,
u
n
)
{\displaystyle x_{2}=x_{2}\left(u_{1},u_{2},\ldots ,u_{n}\right)\ }
x
n
=
x
n
(
u
1
,
u
2
,
…
,
u
n
)
{\displaystyle x_{n}=x_{n}\left(u_{1},u_{2},\ldots ,u_{n}\right)}
Ez egy egyenletrendszer, ami invertálható, tehát megoldható az
u
i
{\displaystyle u_{i}}
u
1
=
u
1
(
x
1
,
x
2
,
…
,
x
n
)
{\displaystyle u_{1}=u_{1}\left(x_{1},x_{2},\ldots ,x_{n}\right)\ }
u
2
=
u
2
(
x
1
,
x
2
,
…
,
x
n
)
{\displaystyle u_{2}=u_{2}\left(x_{1},x_{2},\ldots ,x_{n}\right)\ }
u
n
=
u
n
(
x
1
,
x
2
,
…
,
x
n
)
{\displaystyle u_{n}=u_{n}\left(x_{1},x_{2},\ldots ,x_{n}\right)}
ha az inverz funkcionáldetermináns nem nulla vagy végtelen:
det
(
J
_
_
−
1
)
=
det
∂
(
u
1
,
u
2
,
…
,
u
n
)
∂
(
x
1
,
x
2
,
…
,
x
n
)
≠
0
{\displaystyle \det \left({\underline {\underline {J}}}^{-1}\right)=\det {\frac {\partial (u_{1},u_{2},\ldots ,u_{n})}{\partial (x_{1},x_{2},\ldots ,x_{n})}}\neq 0}
Az inverz transzformációnak is folytonosan differenciálhatónak kell lennie.
A transzformáció reguláris azokban a pontokban, melyeknek egyértelmű a megfeleltetése. A többi pontban szinguláris. Ekkor teljesül, hogy ha egy
P
{\displaystyle P}
(
x
1
,
x
2
,
…
,
x
n
)
{\displaystyle (x_{1},x_{2},\ldots ,x_{n})}
P
{\displaystyle P}
(
u
1
,
u
2
,
…
,
u
n
)
{\displaystyle (u_{1},u_{2},\ldots ,u_{n})}
{
x
i
}
{\displaystyle \{x_{i}\}}
{
u
i
}
{\displaystyle \{u_{i}\}}
Egy transzformációegyenletekre vonatkozó tétel szerint a fent leírtak alapján a Descartes-féle koordináta-rendszerrel együtt definiálható egy görbe vonalú koordináta-rendszer.
Koordinátavonalak, -felületek és tengelyek [ szerkesztés ] Itt ui helyett qi : koordinátavonalak, -felületek és tengelyek (egy kiválasztott hely bázisvektorai szerint) A gömbkoordináta-rendszer koordinátavonalai, -felületei és tengelyei. Felületek: r – gömbök, θ – kúpok, φ – félsíkok; Vonalak: r – egyenes sugarak, θ – vertikális félkörök, φ – horizontális körök; Tengelyek: r – egyenes sugarak, θ – érintők a vertikális félkörökhöz, φ – érintők a horizontális körökhöz Ebben a szakaszban a háromdimenziós térben szemléltetjük a koordinátavonalakat, -felületeket és tengelyeket.
A koordinátafelületek megkaphatók egy koordináta rögzítésével és a többi változtatásával:
r
→
i
j
(
α
,
β
)
=
r
→
(
u
i
=
α
,
u
j
=
β
,
u
k
=
const
)
{\displaystyle {\vec {r}}_{ij}(\alpha ,\beta )={\vec {r}}\,(u_{i}=\alpha ,u_{j}=\beta ,u_{k}={\text{const}})}
i
≠
j
≠
k
≠
i
{\displaystyle i\neq j\neq k\neq i}
Minden nem szinguláris ponton át az
u
k
=
const
{\displaystyle u_{k}={\text{const}}}
A koordinátavonalak úgy kaphatók, hogy két koordinátát rögzítünk, azaz
u
i
=
const
,
u
j
=
const
{\displaystyle u_{i}={\text{const}},\ u_{j}={\text{const}}}
i
≠
j
{\displaystyle i\neq j}
r
→
k
(
γ
)
=
r
→
(
u
i
=
const
,
u
j
=
const
,
u
k
=
γ
)
{\displaystyle {\vec {r}}_{k}(\gamma )={\vec {r}}\,(u_{i}={\text{const}},u_{j}={\text{const}},u_{k}=\gamma )}
i
≠
j
≠
k
≠
i
{\displaystyle i\neq j\neq k\neq i}
A fenti feltétel azt jelenti a funkcionáldetermináns számára, hogy a háromdimenziós tér minden pontján át három koordinátavonalnak kell áthaladnia, különben a pont nem reguláris.
Például a gömbkoordináták esetén a
z
{\displaystyle z}
φ
=
const
{\displaystyle \varphi ={\text{const}}}
φ
{\displaystyle \varphi }
azimut ). Így a
z
{\displaystyle z}
z
=
r
cos
ϑ
{\displaystyle z=r\cos \vartheta }
ϕ
{\displaystyle \phi }
Ha a különböző koordinátavonalak derékszögben metszik egymást, akkor a koordináta-rendszer ortogonális.
A koordinátatengelyeket a koordinátavonalak érintőiként definiáljuk. Ez a Descartes-féle koordináta-rendszertől és az affin koordináta-rendszerektől különböző koordináta-rendszerekben azt jelenti, hogy a tengelyek függnek a helytől. Emiatt helyi koordinátákról beszélünk.
Egy vektor koordinátákkal való ábrázolásához bázisra van szükség. Ehhez egy
n
{\displaystyle n}
n
{\displaystyle n}
Csak egyenesvonalú esetben állandóak a bázisvektorok; valóban görbe vonalú koordináta-rendszer esetén a bázis, így a koordináták is függenek a helytől. Emiatt ezeket a bázisokat helyi bázisoknak nevezik. Mind a bázisvektorok, mind a koordináták helyfüggők. Egyenes vonalú koordináta-rendszerekben a bázis globális, azaz nem függ a helytől. A helytől kizárólag a koordináták függnek.
Helyi bázis előállítására két módszer létezik:
kovariáns bázis
kontravariáns bázis A két bázis reciprok, illetve duális egymással. Holonóm bázisoknak is nevezik őket. Különböznek abban, hogyan transzformálódnak koordinátaváltáskor – a két transzformáció inverze egymásnak.
Az adott sokaság minden pontjában egyidejűleg létezik mindkét bázis. Így egy tetszőleges vektor ábrázolható egyikben vagy másikban. Az
a
u
i
{\displaystyle a_{u_{i}}}
b
→
u
i
{\displaystyle {\vec {b}}_{u_{i}}}
a
u
i
∗
{\displaystyle a_{u_{i}}^{\,*}}
b
→
u
i
∗
{\displaystyle {\vec {b}}_{u_{i}}^{\,*}}
a
→
=
∑
i
=
1
n
a
u
i
b
→
u
i
=
∑
i
=
1
n
a
u
i
∗
b
→
u
i
∗
{\displaystyle {\vec {a}}=\sum \limits _{i=1}^{n}a_{u_{i}}{\vec {b}}_{u_{i}}=\sum \limits _{i=1}^{n}a_{u_{i}}^{\,*}{\vec {b}}_{u_{i}}^{\,*}}
Ez a keresztbe párosítás biztosítja, hogy
a
→
{\displaystyle {\vec {a}}}
Egy vektor (koordinátavektor) kontravariáns, ha a koordináták kontravariánsak, és a bázis kovariáns. Egy vektor (koordinátavektor) kovariáns, ha a koordináták kovariánsak, és a bázis kontravariáns.
Egy v vektor (pirossal sárgával , balra:e 1 , e 2 , e 3 ), érintővektorok a koordinátagörbékhez (feketével ) és • egy kovektor bázisban vagy kobázisban (kékkel , jobbra:e 1 , e 2 , e 3 ), normálvektorok a koordinátafelületekhez (szürkével általános (nem feltétlenül ortogonális) görbe vonalú (q 1 , q 2 , q 3 ) koordinátákban. A bázis és a kobázis nem egyezik, kivéve, ha a rendszer ortogonális[2] A kovariáns bázis vektorai minden pontban érintőlegesek valamelyik koordinátavonalhoz.
Normált és természetes bázis [ szerkesztés ] A koordinátavonalak érintő-egységvektorai bázist alkotnak, ami kovariáns bázisvektorokból áll:
e
→
u
i
=
∂
r
→
∂
u
i
|
∂
r
→
∂
u
i
|
{\displaystyle {\vec {e}}_{u_{i}}={\frac {\frac {\partial {\vec {r}}}{\partial u_{i}}}{\left|{\frac {\partial {\vec {r}}}{\partial u_{i}}}\right|}}}
Ezek az egységvektorok a helytől függően fordulnak
e
→
u
i
=
e
→
u
i
(
u
1
,
u
2
,
…
,
u
n
)
{\displaystyle {\vec {e}}_{u_{i}}={\vec {e}}_{u_{i}}\left(u_{1},u_{2},\ldots ,u_{n}\right)}
A
h
u
i
{\displaystyle h_{u_{i}}}
h
u
i
:=
|
∂
r
→
∂
u
i
|
{\displaystyle h_{u_{i}}:=\left|{\frac {\partial {\vec {r}}}{\partial u_{i}}}\right|}
e
→
u
i
=
1
h
u
i
∂
r
→
∂
u
i
{\displaystyle \displaystyle {\vec {e}}_{u_{i}}={\frac {1}{h_{u_{i}}}}{\frac {\partial {\vec {r}}}{\partial u_{i}}}}
A nem normált vektorok alkotják a természetes bázist, amiből a normálással a normált bázis nyerhető. Itt a természetes bázis vektorait
b
→
u
i
{\displaystyle {\vec {b}}_{u_{i}}}
e
→
u
i
{\displaystyle {\vec {e}}_{u_{i}}}
b
→
u
i
=
∂
r
→
∂
u
i
=
h
u
i
e
→
u
i
{\displaystyle {\vec {b}}_{u_{i}}={\frac {\partial {\vec {r}}}{\partial u_{i}}}=h_{u_{i}}{\vec {e}}_{u_{i}}}
Kontravariáns koordináták [ szerkesztés ] Az új bázisokkal az összes
a
→
{\displaystyle {\vec {a}}}
e
→
u
i
{\displaystyle {\vec {e}}_{u_{i}}}
b
→
u
i
{\displaystyle {\vec {b}}_{u_{i}}}
a
→
=
∑
i
=
1
n
a
u
i
e
→
u
i
=
∑
i
=
1
n
a
~
u
i
b
→
u
i
ahol
a
~
u
i
=
a
u
i
h
u
i
,
b
→
u
i
=
h
u
i
e
→
u
i
{\displaystyle {\vec {a}}=\sum \limits _{i=1}^{n}{a_{u_{i}}{\vec {e}}_{u_{i}}}=\sum \limits _{i=1}^{n}{{\tilde {a}}_{u_{i}}{\vec {b}}_{u_{i}}}\quad {\text{ahol}}\quad {\tilde {a}}_{u_{i}}={\frac {a_{u_{i}}}{h_{u_{i}}}},\quad {\vec {b}}_{u_{i}}=h_{u_{i}}{\vec {e}}_{u_{i}}}
ahol
a
u
i
{\displaystyle a_{u_{i}}}
a
~
u
i
{\displaystyle {\tilde {a}}_{u_{i}}}
u
i
{\displaystyle u_{i}}
a
u
i
{\displaystyle a_{u_{i}}}
a
~
u
i
{\displaystyle {\tilde {a}}_{u_{i}}}
a
~
u
i
{\displaystyle {\tilde {a}}_{u_{i}}}
a
i
{\displaystyle a^{i}}
Egy
a
u
i
e
→
u
i
=
a
~
u
i
b
→
u
i
{\displaystyle {a_{u_{i}}{\vec {e}}_{u_{i}}}={{\tilde {a}}_{u_{i}}{\vec {b}}_{u_{i}}}}
a
u
i
{\displaystyle a_{u_{i}}}
a
~
u
i
{\displaystyle {\tilde {a}}_{u_{i}}}
b
→
u
i
{\displaystyle {\vec {b}}_{u_{i}}}
|
a
u
i
|
=
|
a
u
i
e
→
u
i
|
=
|
a
~
u
i
b
→
u
i
|
=
|
a
~
u
i
|
|
b
→
u
i
|
=
|
a
~
u
i
|
|
h
u
i
|
{\displaystyle |a_{u_{i}}|=|a_{u_{i}}{\vec {e}}_{u_{i}}|=|{\tilde {a}}_{u_{i}}{\vec {b}}_{u_{i}}|=|{\tilde {a}}_{u_{i}}|\,|{\vec {b}}_{u_{i}}|=|{\tilde {a}}_{u_{i}}|\,|h_{u_{i}}|}
Ha a vektor fizikai mennyiséget jelöl, akkor a természetes bázis hossza tartalmazhat mértékegységet is, ami így összeszorzódik a koordinátákkal. Ez körülményes lehet. Normált bázis esetén azonban a mértékegység teljes egészében a koordinátán múlik. Ezért az
a
u
i
{\displaystyle a_{u_{i}}}
e
→
u
i
{\displaystyle {\vec {e}}_{u_{i}}}
Megkülönböztetésként az
a
~
u
i
{\displaystyle {\tilde {a}}_{u_{i}}}
b
→
u
i
{\displaystyle {\vec {b}}_{u_{i}}}
A bázisvektorok és koordináták viselkedése a transzformáció során, Jacobi-mátrix [ szerkesztés ] Helyi kovariáns bázis transzformációja általános görbe vonalú koordináták esetén A természetes bázisvektorok definíciójából következően az
{
u
i
}
{\displaystyle \{u_{i}\}}
{
x
i
}
{\displaystyle \{x_{i}\}}
b
→
u
k
=
∂
r
→
∂
u
k
=
∑
j
∂
x
j
∂
u
k
∂
r
→
∂
x
j
=
∑
j
∂
x
j
∂
u
k
e
→
x
j
{\displaystyle {\vec {b}}_{u_{k}}={\frac {\partial {\vec {r}}}{\partial u_{k}}}=\sum _{j}{\frac {\partial x_{j}}{\partial u_{k}}}{\frac {\partial {\vec {r}}}{\partial x_{j}}}=\sum _{j}{\frac {\partial x_{j}}{\partial u_{k}}}{\vec {e}}_{x_{j}}}
A természetes bázisvektorok egyszerűen viselkednek a transzformáció során. Normált bázis esetén a
h
u
i
{\displaystyle h_{u_{i}}}
b
→
u
k
=
∑
j
∂
x
j
∂
u
k
e
→
x
j
⟹
h
u
k
e
→
u
k
=
∑
j
∂
x
j
∂
u
k
e
→
x
j
{\displaystyle {\vec {b}}_{u_{k}}=\sum _{j}{\frac {\partial x_{j}}{\partial u_{k}}}{\vec {e}}_{x_{j}}\quad \Longrightarrow \quad h_{u_{k}}{\vec {e}}_{u_{k}}=\sum _{j}{\frac {\partial x_{j}}{\partial u_{k}}}{\vec {e}}_{x_{j}}}
Egy tetszőleges
a
→
{\displaystyle {\vec {a}}}
a
→
=
∑
i
a
x
i
e
→
x
i
=
∑
i
,
k
a
x
i
δ
i
k
e
→
x
k
=
∑
i
,
j
,
k
a
x
i
∂
u
j
∂
x
i
∂
x
k
∂
u
j
e
→
x
k
=
∑
i
,
j
a
x
i
∂
u
j
∂
x
i
b
→
u
j
=
∑
j
a
~
u
j
b
→
u
j
{\displaystyle {\vec {a}}=\sum _{i}a_{x_{i}}{\vec {e}}_{x_{i}}=\sum _{i,k}a_{x_{i}}\delta _{ik}{\vec {e}}_{x_{k}}=\sum _{i,j,k}a_{x_{i}}{\frac {\partial u_{j}}{\partial x_{i}}}{\frac {\partial x_{k}}{\partial u_{j}}}{\vec {e}}_{x_{k}}=\sum _{i,j}a_{x_{i}}{\frac {\partial u_{j}}{\partial x_{i}}}{\vec {b}}_{u_{j}}=\sum _{j}{\tilde {a}}_{u_{j}}{\vec {b}}_{u_{j}}}
Így kapható a koordináták viselkedése a transzformáció során:
a
~
u
i
=
∑
j
a
x
j
∂
u
i
∂
x
j
⟹
a
u
i
h
u
i
=
∑
j
a
x
j
∂
u
i
∂
x
j
{\displaystyle {\tilde {a}}_{u_{i}}=\sum _{j}a_{x_{j}}{\frac {\partial u_{i}}{\partial x_{j}}}\quad \Longrightarrow \quad {\frac {a_{u_{i}}}{h_{u_{i}}}}=\sum _{j}a_{x_{j}}{\frac {\partial u_{i}}{\partial x_{j}}}}
Míg a kovariáns vektorok esetén a
J
k
j
=
∂
x
j
∂
u
k
{\displaystyle J_{kj}={\tfrac {\partial x_{j}}{\partial u_{k}}}}
J
k
j
−
1
=
∂
u
j
∂
x
k
{\displaystyle J_{kj}^{-1}={\tfrac {\partial u_{j}}{\partial x_{k}}}}
A tenzoranalízisben a vektorok viselkedését a fenti transzformációs viselkedéssel definiálják. Maga a
r
→
{\displaystyle {\vec {r}}}
d
r
→
=
∑
i
b
→
u
i
d
u
i
{\displaystyle \textstyle \mathrm {d} {\vec {r}}=\sum _{i}{\vec {b}}_{u_{i}}\mathrm {d} u_{i}}
A Descartes-féle koordináták transzformációjának Jacobi-mátrixa megegyezik azzal a mátrixszal, melyben a természetes bázis oszlopvektorokként szerepel:
J
_
_
=
∂
(
x
1
,
x
2
,
…
,
x
n
)
∂
(
u
1
,
u
2
,
…
,
u
n
)
=
(
∂
x
1
/
∂
u
1
∂
x
1
/
∂
u
2
…
∂
x
1
/
∂
u
n
∂
x
2
/
∂
u
1
∂
x
2
/
∂
u
2
…
∂
x
2
/
∂
u
n
⋮
⋮
⋮
∂
x
n
/
∂
u
1
∂
x
n
/
∂
u
2
…
∂
x
n
/
∂
u
n
)
=
(
|
|
|
b
→
u
1
b
→
u
2
…
b
→
u
n
|
|
|
)
≡
[
b
→
u
1
,
b
→
u
2
,
…
,
b
→
u
n
]
{\displaystyle {\underline {\underline {J}}}={\frac {\partial (x_{1},x_{2},\ldots ,x_{n})}{\partial (u_{1},u_{2},\ldots ,u_{n})}}=\left({\begin{array}{cccc}\partial x_{1}/\partial u_{1}&\partial x_{1}/\partial u_{2}&\ldots &\partial x_{1}/\partial u_{n}\\\partial x_{2}/\partial u_{1}&\partial x_{2}/\partial u_{2}&\ldots &\partial x_{2}/\partial u_{n}\\\vdots &\vdots &&\vdots \\\partial x_{n}/\partial u_{1}&\partial x_{n}/\partial u_{2}&\ldots &\partial x_{n}/\partial u_{n}\end{array}}\right)=\left({\begin{array}{cccc}|&|&&|\\{\vec {b}}_{u_{1}}&{\vec {b}}_{u_{2}}&\ldots &{\vec {b}}_{u_{n}}\\|&|&&|\end{array}}\right)\equiv [{\vec {b}}_{u_{1}},{\vec {b}}_{u_{2}},\ldots ,{\vec {b}}_{u_{n}}]}
Az inverz funkcionáldeterminánsra vonatkozó
det
(
J
_
_
−
1
)
≠
0
{\displaystyle \det \left({\underline {\underline {J}}}^{-1}\right)\neq 0}
e
→
x
k
=
∑
j
∂
u
j
∂
x
k
b
→
u
j
=
∑
j
(
J
−
1
)
k
j
b
→
u
j
{\displaystyle {\vec {e}}_{x_{k}}=\sum _{j}{\frac {\partial u_{j}}{\partial x_{k}}}{\vec {b}}_{u_{j}}=\sum _{j}(J^{-1})_{kj}{\vec {b}}_{u_{j}}}
Ez megfelel az
b
→
=
A
_
_
v
→
{\displaystyle {\vec {b}}={\underline {\underline {A}}}{\vec {v}}}
v
→
{\displaystyle {\vec {v}}}
v
→
{\displaystyle {\vec {v}}}
{
b
→
u
j
}
{\displaystyle \{{\vec {b}}_{u_{j}}\}}
A
_
_
{\displaystyle {\underline {\underline {A}}}}
det
A
_
_
{\displaystyle \det {\underline {\underline {A}}}}
{
b
→
u
j
}
{\displaystyle \{{\vec {b}}_{u_{j}}\}}
A duális
{
b
→
u
i
∗
}
{\displaystyle \{{\vec {b}}_{u_{i}}^{*}\}}
Metrikus tenzor és Gram-determináns [ szerkesztés ] A természetes bázisvektorok skalárszorzatai definiálják a
g
{\displaystyle g}
metrikus tenzor komponenseit:
g
i
j
=
b
→
u
i
⋅
b
→
u
j
=
h
u
i
h
u
j
e
→
u
i
⋅
e
→
u
j
=
h
u
i
h
u
j
cos
(
∢
(
e
→
u
i
,
e
→
u
j
)
)
{\displaystyle g_{ij}={\vec {b}}_{u_{i}}\cdot {\vec {b}}_{u_{j}}=h_{u_{i}}h_{u_{j}}{\vec {e}}_{u_{i}}\cdot {\vec {e}}_{u_{j}}=h_{u_{i}}h_{u_{j}}\cos \!\left(\sphericalangle ({\vec {e}}_{u_{i}},{\vec {e}}_{u_{j}})\right)}
Vegyük észre, hogy a metrikus tenzor a skaláris szorzás kommutativitás miatt szimmetrikus:
g
i
j
=
b
→
u
i
⋅
b
→
u
j
=
b
→
u
j
⋅
b
→
u
i
=
g
j
i
{\displaystyle g_{ij}={\vec {b}}_{u_{i}}\cdot {\vec {b}}_{u_{j}}={\vec {b}}_{u_{j}}\cdot {\vec {b}}_{u_{i}}=g_{ji}}
Emiatt a metrikus tenzornak
N
(
N
+
1
)
/
2
{\displaystyle N(N+1)/2}
N
2
{\displaystyle N^{2}}
A metrikus tenzor írható, mint a Jacobi-mátrix és transzponáltjának szorzata:
g
_
_
=
J
_
_
T
J
_
_
=
[
b
→
u
1
,
b
→
u
2
,
…
,
b
→
u
n
]
T
[
b
→
u
1
,
b
→
u
2
,
…
,
b
→
u
n
]
=
(
b
→
u
1
⋅
b
→
u
1
…
b
→
u
1
⋅
b
→
u
n
⋮
⋮
b
→
u
n
⋅
b
→
u
1
…
b
→
u
n
⋅
b
→
u
n
)
{\displaystyle {\underline {\underline {g}}}={\underline {\underline {J}}}^{T}{\underline {\underline {J}}}=[{\vec {b}}_{u_{1}},{\vec {b}}_{u_{2}},\ldots ,{\vec {b}}_{u_{n}}]^{T}[{\vec {b}}_{u_{1}},{\vec {b}}_{u_{2}},\ldots ,{\vec {b}}_{u_{n}}]=\left({\begin{array}{ccc}{\vec {b}}_{u_{1}}\cdot {\vec {b}}_{u_{1}}&\ldots &{\vec {b}}_{u_{1}}\cdot {\vec {b}}_{u_{n}}\\\vdots &&\vdots \\{\vec {b}}_{u_{n}}\cdot {\vec {b}}_{u_{1}}&\ldots &{\vec {b}}_{u_{n}}\cdot {\vec {b}}_{u_{n}}\end{array}}\right)}
A
g
i
j
{\displaystyle g_{ij}}
{
a
~
u
i
}
{\displaystyle \{{\tilde {a}}_{u_{i}}\}}
skálázási tényezők .
A
h
u
i
{\displaystyle h_{u_{i}}}
g
i
i
{\displaystyle g_{ii}}
|
b
→
u
i
|
=
b
→
u
i
⋅
b
→
u
i
{\displaystyle |{\vec {b}}_{u_{i}}|={\sqrt {{\vec {b}}_{u_{i}}\cdot {\vec {b}}_{u_{i}}}}}
h
u
i
=
g
i
i
{\displaystyle h_{u_{i}}={\sqrt {g_{ii}}}}
A metrikus tenzor determinánsa a
g
{\displaystyle g}
Gram-determináns :
det
g
_
_
=
g
{\displaystyle \det {\underline {\underline {g}}}=g}
g
=
det
(
J
T
J
)
=
det
J
T
det
J
=
(
det
J
)
2
{\displaystyle g=\det(J^{T}J)=\det J^{T}\det J=(\det J)^{2}}
det
[
b
→
u
1
,
b
→
u
2
,
…
,
b
→
u
n
]
≡
det
J
=
±
g
{\displaystyle \det[{\vec {b}}_{u_{1}},{\vec {b}}_{u_{2}},\ldots ,{\vec {b}}_{u_{n}}]\equiv \det J=\pm {\sqrt {g}}}
ahol az előjel a bázis irányításától függ. A normált bázisvektorokból alkotott determináns a multilinearitás miatt adja, hogy:
det
[
e
→
u
1
,
e
→
u
2
,
…
,
e
→
u
n
]
=
det
[
h
u
1
−
1
b
→
u
1
,
h
u
2
−
1
b
→
u
2
,
…
,
h
u
n
−
1
b
→
u
n
]
=
det
[
b
→
u
1
,
b
→
u
2
,
…
,
b
→
u
n
]
h
u
1
h
u
2
⋯
h
u
n
=
±
g
h
u
1
h
u
2
⋯
h
u
n
{\displaystyle \det[{\vec {e}}_{u_{1}},{\vec {e}}_{u_{2}},\ldots ,{\vec {e}}_{u_{n}}]=\det[h_{u_{1}}^{-1}{\vec {b}}_{u_{1}},h_{u_{2}}^{-1}{\vec {b}}_{u_{2}},\ldots ,h_{u_{n}}^{-1}{\vec {b}}_{u_{n}}]={\frac {\det[{\vec {b}}_{u_{1}},{\vec {b}}_{u_{2}},\ldots ,{\vec {b}}_{u_{n}}]}{h_{u_{1}}h_{u_{2}}\cdots h_{u_{n}}}}={\frac {\pm {\sqrt {g}}}{h_{u_{1}}h_{u_{2}}\cdots h_{u_{n}}}}}
A metrikus tenzor
g
i
j
{\displaystyle g^{ij}}
Cramer-szabály miatt, hogy:
g
i
j
:=
(
g
−
1
)
i
j
=
A
i
j
g
{\displaystyle g^{ij}:=(g^{-1})_{ij}={\frac {A^{ij}}{g}}}
ahol
A
i
j
{\displaystyle A^{ij}}
g
{\displaystyle g}
g
:=
det
g
_
_
=
∑
i
,
j
g
i
j
A
j
i
⟹
∂
g
∂
g
i
j
=
A
j
i
{\displaystyle g:=\det {\underline {\underline {g}}}=\sum _{i,j}g_{ij}A^{ji}\quad \Longrightarrow \quad {\frac {\partial g}{\partial g_{ij}}}=A^{ji}}
és az inverz metrikus tenzorra:
g
i
j
=
1
g
∂
g
∂
g
j
i
{\displaystyle g^{ij}={\frac {1}{g}}{\frac {\partial g}{\partial g_{ji}}}}
Ortogonális koordináta-rendszerek [ szerkesztés ] Ha az
n
{\displaystyle n}
n
{\displaystyle n}
e
→
u
i
{\displaystyle {\vec {e}}_{u_{i}}}
R
n
{\displaystyle \mathbb {R} ^{n}}
e
→
u
i
⋅
e
→
u
j
=
δ
i
j
{\displaystyle {\vec {e}}_{u_{i}}\cdot {\vec {e}}_{u_{j}}=\delta _{ij}}
i
,
j
=
1
,
2
,
…
,
n
{\displaystyle i,j=1,2,\ldots ,n}
δ
:
{\displaystyle \delta :\ }
Kronecker-delta )A természetes bázisvektorokra:
g
i
j
=
b
→
u
i
⋅
b
→
u
j
=
h
u
i
h
u
j
δ
i
j
=
h
u
i
2
δ
i
j
{\displaystyle g_{ij}={\vec {b}}_{u_{i}}\cdot {\vec {b}}_{u_{j}}=h_{u_{i}}h_{u_{j}}\delta _{ij}=h_{u_{i}}^{2}\delta _{ij}}
Így az ortogonális bázisvektorok esetén a metrikus tenzor diagonális:
g
_
_
=
(
h
u
1
2
0
…
0
0
h
u
2
2
…
0
⋮
⋮
⋮
0
0
…
h
u
3
2
)
{\displaystyle {\underline {\underline {g}}}=\left({\begin{array}{cccc}h_{u_{1}}^{2}&0&\ldots &0\\0&h_{u_{2}}^{2}&\ldots &0\\\vdots &\vdots &&\vdots \\0&0&\ldots &h_{u_{3}}^{2}\end{array}}\right)}
Az inverz metrikus tenzor ortognális koordináták esetén:
(
g
−
1
)
i
j
≡
g
i
j
=
h
u
i
−
2
δ
i
j
{\displaystyle (g^{-1})_{ij}\equiv g^{ij}=h_{u_{i}}^{-2}\delta _{ij}}
g
_
_
−
1
=
(
1
/
h
u
1
2
0
…
0
0
1
/
h
u
2
2
…
0
⋮
⋮
⋮
0
0
…
1
/
h
u
n
2
)
{\displaystyle {\underline {\underline {g}}}^{-1}=\left({\begin{array}{cccc}1/h_{u_{1}}^{2}&0&\ldots &0\\0&1/h_{u_{2}}^{2}&\ldots &0\\\vdots &\vdots &&\vdots \\0&0&\ldots &1/h_{u_{n}}^{2}\end{array}}\right)}
A Gram-determináns is egyszerűbb:
g
=
h
u
1
2
h
u
2
2
⋯
h
u
n
2
{\displaystyle g=h_{u_{1}}^{2}h_{u_{2}}^{2}\cdots h_{u_{n}}^{2}}
A természetes, illetve normált bázisvektorok esetén a determináns:
det
[
b
→
u
1
,
b
→
u
2
,
…
,
b
→
u
n
]
=
g
=
h
u
1
h
u
2
⋯
h
u
3
⟺
det
[
e
→
u
1
,
e
→
u
2
,
…
,
e
→
u
n
]
=
1
{\displaystyle \det[{\vec {b}}_{u_{1}},{\vec {b}}_{u_{2}},\ldots ,{\vec {b}}_{u_{n}}]={\sqrt {g}}=h_{u_{1}}h_{u_{2}}\cdots h_{u_{3}}\quad \iff \quad \det[{\vec {e}}_{u_{1}},{\vec {e}}_{u_{2}},\ldots ,{\vec {e}}_{u_{n}}]=1}
Ha az ortonormált bázis jobbkezes, akkor teljesülnek a következők:
e
→
u
i
×
e
→
u
j
=
ε
i
j
k
e
→
u
k
{\displaystyle {\vec {e}}_{u_{i}}\times {\vec {e}}_{u_{j}}=\varepsilon _{ijk}{\vec {e}}_{u_{k}}}
i
,
j
,
k
=
1
,
2
,
3
{\displaystyle i,j,k=1,2,3}
ε
{\displaystyle \varepsilon }
Levi-Civita-szimbólum )Bővebben:
e
→
u
1
×
e
→
u
2
=
e
→
u
3
e
→
u
2
×
e
→
u
3
=
e
→
u
1
e
→
u
3
×
e
→
u
1
=
e
→
u
2
e
→
u
2
×
e
→
u
1
=
−
e
→
u
3
e
→
u
3
×
e
→
u
2
=
−
e
→
u
1
e
→
u
1
×
e
→
u
3
=
−
e
→
u
2
{\displaystyle {\begin{aligned}{\vec {e}}_{u_{1}}\times {\vec {e}}_{u_{2}}&={\vec {e}}_{u_{3}}\quad &{\vec {e}}_{u_{2}}\times {\vec {e}}_{u_{3}}&={\vec {e}}_{u_{1}}\quad &{\vec {e}}_{u_{3}}\times {\vec {e}}_{u_{1}}&={\vec {e}}_{u_{2}}\\{\vec {e}}_{u_{2}}\times {\vec {e}}_{u_{1}}&=-{\vec {e}}_{u_{3}}&{\vec {e}}_{u_{3}}\times {\vec {e}}_{u_{2}}&=-{\vec {e}}_{u_{1}}&{\vec {e}}_{u_{1}}\times {\vec {e}}_{u_{3}}&=-{\vec {e}}_{u_{2}}\end{aligned}}}
Egyenes vonalú koordináta-rendszerek [ szerkesztés ] Általában a görbe vonalú koordináta-rendszerekben nincs globális bázis, mivel a koordinátavonalak nem egyenesek. Globális bázis csak abban a speciális esetben létezik, hogyha a koordinátavonalak egyenesek. Ekkor a koordinátafelületek síkok, seregeik párhuzamos síkseregeket alkotnak. Ekkor a transzformációs egyenletek így alakulnak:
x
i
=
∑
j
=
1
n
A
i
j
u
j
+
b
i
⟺
J
i
j
≡
∂
x
i
∂
u
j
=
A
i
j
{\displaystyle x_{i}=\sum _{j=1}^{n}A_{ij}u_{j}+b_{i}\quad \iff \quad J_{ij}\equiv {\frac {\partial x_{i}}{\partial u_{j}}}=A_{ij}}
ahol
A
i
j
{\displaystyle A_{ij}}
b
i
{\displaystyle b_{i}}
J
{\displaystyle J}
A
{\displaystyle A}
b
→
u
i
{\displaystyle {\vec {b}}_{u_{i}}}
A
{\displaystyle A}
i
{\displaystyle i}
Duális bázis: kontravariáns bázis [ szerkesztés ] A kontravariőns bázisvektorok minden pontban merőlegesek a megfelelő koordinátafelületekre. Duálisak a kovariáns bázisvektorokra. Egy vektor kontravariáns komponensei megkaphatók a kontravariáns bázisvektorokra való vetítéssel.
Ortogonális koordináták [ szerkesztés ] A
a
→
=
∑
j
=
1
n
a
u
j
e
→
u
j
{\displaystyle {\vec {a}}=\sum \limits _{j=1}^{n}{a_{u_{j}}{\vec {e}}_{u_{j}}}}
a
u
i
{\displaystyle a_{u_{i}}}
e
→
u
i
⋅
e
→
u
j
=
δ
i
j
{\displaystyle {\vec {e}}_{u_{i}}\cdot {\vec {e}}_{u_{j}}=\delta _{ij}}
e
→
u
i
⋅
a
→
=
∑
j
=
1
n
a
u
j
e
→
u
i
⋅
e
→
u
j
=
∑
j
=
1
n
a
u
j
δ
i
j
=
a
u
i
{\displaystyle {\vec {e}}_{u_{i}}\cdot {\vec {a}}=\sum \limits _{j=1}^{n}{a_{u_{j}}{\vec {e}}_{u_{i}}\cdot {\vec {e}}_{u_{j}}}=\sum \limits _{j=1}^{n}{a_{u_{j}}\delta _{ij}}=a_{u_{i}}}
Nem derékszögű koordináta-rendszerekben egy vektor egy kovariáns koordinátája megkapható a
e
→
u
i
⋅
a
→
{\displaystyle {\vec {e}}_{u_{i}}\cdot {\vec {a}}}
a
u
i
{\displaystyle a_{u_{i}}}
e
→
u
i
⋅
e
→
u
j
=
δ
i
j
{\displaystyle {\vec {e}}_{u_{i}}\cdot {\vec {e}}_{u_{j}}=\delta _{ij}}
metrikus tenzor nem diagonális. Ehhez szükség van a duális tér és a duális bázis fogalmára.
Duális tér és duális bázis [ szerkesztés ] Az érintővektorok
V
{\displaystyle V}
V
∗
{\displaystyle V^{*}}
f
:
V
→
K
,
v
→
↦
f
[
v
→
]
{\displaystyle f\colon \ V\rightarrow K,\ {\vec {v}}\mapsto f[{\vec {v}}]}
V
∗
{\displaystyle V^{*}}
V
{\displaystyle V}
e
→
i
∗
[
e
→
j
]
=
δ
i
j
{\displaystyle {\vec {e}}_{i}^{\,*}[{\vec {e}}_{j}]=\delta _{ij}}
Definiáljuk továbbá a következő bilineáris formát:
⟨
⋅
,
⋅
⟩
:
V
∗
×
V
→
K
,
⟨
f
,
v
→
⟩
=
f
[
v
→
]
{\displaystyle \langle \cdot ,\cdot \rangle \colon \ V^{*}\times V\rightarrow K,\ \langle f,{\vec {v}}\rangle =f[{\vec {v}}]}
e
→
i
∗
∈
V
∗
{\displaystyle {\vec {e}}_{i}^{\,*}\in V^{\,*}}
e
→
j
∈
V
{\displaystyle {\vec {e}}_{j}\in V}
⟨
e
→
i
∗
,
e
→
j
⟩
=
δ
i
j
{\displaystyle \langle {\vec {e}}_{i}^{\,*},{\vec {e}}_{j}\rangle =\delta _{ij}}
Véges dimenziós
V
{\displaystyle V}
V
∗
{\displaystyle V^{*}}
V
{\displaystyle V}
V
≅
V
∗
{\displaystyle V\cong V^{\,*}}
E
n
{\displaystyle E^{n}}
R
n
{\displaystyle \mathbb {R} ^{n}}
⟨
w
→
∗
,
v
→
⟩
=
∑
i
=
1
n
w
i
∗
v
i
≡
w
→
∗
⋅
v
→
=
w
→
g
_
_
v
→
{\displaystyle \langle {\vec {w}}^{\,*},{\vec {v}}\rangle =\sum _{i=1}^{n}w_{i}^{\,*}\,v_{i}\equiv {\vec {w}}^{\,*}\cdot {\vec {v}}={\vec {w}}{\underline {\underline {g}}}{\vec {v}}}
skalárszorzattal, így a duális vektorok azonosíthatók vektorokként. Itt
K
=
R
{\displaystyle K=\mathbb {R} }
V
=
R
n
{\displaystyle V=\mathbb {R} ^{n}}
V
∗
=
R
n
{\displaystyle V^{\,*}=\mathbb {R} ^{n}}
A duális bázist úgy definiálják, hogy a
e
→
u
j
{\displaystyle {\vec {e}}_{u_{j}}}
e
→
u
i
∗
{\displaystyle {\vec {e}}_{u_{i}}^{\ *}}
e
→
u
j
{\displaystyle {\vec {e}}_{u_{j}}}
e
→
u
i
∗
⋅
e
→
u
j
=
δ
i
j
ahol
b
→
u
j
=
h
u
j
e
→
u
j
,
b
→
u
i
∗
=
1
h
u
i
e
→
u
i
∗
{\displaystyle {\vec {e}}_{u_{i}}^{\ *}\cdot {\vec {e}}_{u_{j}}=\delta _{ij}\quad {\text{ahol}}\quad {\vec {b}}_{u_{j}}=h_{u_{j}}{\vec {e}}_{u_{j}}\ ,\quad {\vec {b}}_{u_{i}}^{\ *}={\frac {1}{h_{u_{i}}}}{\vec {e}}_{u_{i}}^{\ *}}
legyen. Hasonlóan, a
b
→
u
j
{\displaystyle {\vec {b}}_{u_{j}}}
b
→
u
i
∗
{\displaystyle {\vec {b}}_{u_{i}}^{\ *}}
b
→
u
i
∗
⋅
b
→
u
j
=
δ
i
j
{\displaystyle {\vec {b}}_{u_{i}}^{\ *}\cdot {\vec {b}}_{u_{j}}=\delta _{ij}}
A
b
→
u
j
{\displaystyle {\vec {b}}_{u_{j}}}
e
→
u
i
∗
{\displaystyle {\vec {e}}_{u_{i}}^{\ *}}
[
b
→
u
1
∗
,
b
→
u
2
∗
,
…
,
b
→
u
n
∗
]
T
[
b
→
u
1
,
b
→
u
2
,
…
,
b
→
u
n
]
=
E
_
_
{\displaystyle [{\vec {b}}_{u_{1}}^{\ *},{\vec {b}}_{u_{2}}^{\ *},\ldots ,{\vec {b}}_{u_{n}}^{\ *}]^{T}[{\vec {b}}_{u_{1}},{\vec {b}}_{u_{2}},\ldots ,{\vec {b}}_{u_{n}}]={\underline {\underline {E}}}}
Mivel a kovariáns bázisvektorokból, mint oszlopokból alkotott Jacobi-mátrix megfelel annak, hogy
J
_
_
=
[
b
→
u
1
,
b
→
u
2
,
…
,
b
→
u
n
]
{\displaystyle {\underline {\underline {J}}}=[{\vec {b}}_{u_{1}},{\vec {b}}_{u_{2}},\ldots ,{\vec {b}}_{u_{n}}]}
J
_
_
−
1
=
[
b
→
u
1
∗
,
b
→
u
2
∗
,
…
,
b
→
u
n
∗
]
T
{\displaystyle {\underline {\underline {J}}}^{-1}=[{\vec {b}}_{u_{1}}^{\ *},{\vec {b}}_{u_{2}}^{\ *},\ldots ,{\vec {b}}_{u_{n}}^{\ *}]^{T}}
Tehát a duális bázisvektorok megkaphatók a Jacobi-mátrix invertálásával.
A kontravariáns bázisvektorok Gram-determinánsa megegyezik a kovariáns bázisvektorokból alkotott mátrix determinánsának inverzével:
det
[
b
→
u
1
∗
,
b
→
u
2
∗
,
…
,
b
→
u
n
∗
]
T
=
det
(
J
−
1
)
=
1
det
(
J
)
=
1
g
{\displaystyle \det[{\vec {b}}_{u_{1}}^{\ *},{\vec {b}}_{u_{2}}^{\ *},\ldots ,{\vec {b}}_{u_{n}}^{\ *}]^{T}=\det(J^{-1})={\frac {1}{\det(J)}}={\frac {1}{\sqrt {g}}}}
Kovariáns komponensek [ szerkesztés ] Az új bázisban az összes
a
→
{\displaystyle {\vec {a}}}
e
→
u
i
∗
{\displaystyle {\vec {e}}_{u_{i}}^{\ *}}
b
→
u
i
∗
{\displaystyle {\vec {b}}_{u_{i}}^{\ *}}
a
→
=
∑
i
=
1
n
a
u
i
∗
e
→
u
i
∗
=
∑
i
=
1
n
a
~
u
i
∗
b
→
u
i
∗
ahol
a
~
u
i
∗
=
h
u
i
a
u
i
∗
,
b
→
u
i
∗
=
1
h
u
i
e
→
u
i
∗
{\displaystyle {\vec {a}}=\sum \limits _{i=1}^{n}{a_{u_{i}}^{\ *}{\vec {e}}_{u_{i}}^{\ *}}=\sum \limits _{i=1}^{n}{{\tilde {a}}_{u_{i}}^{\ *}{\vec {b}}_{u_{i}}^{\ *}}\quad {\text{ahol}}\quad {\tilde {a}}_{u_{i}}^{\ *}=h_{u_{i}}a_{u_{i}}^{\ *},\quad {\vec {b}}_{u_{i}}^{\ *}={\frac {1}{h_{u_{i}}}}{\vec {e}}_{u_{i}}^{\ *}}
Itt
a
u
i
∗
{\displaystyle a_{u_{i}}^{\ *}}
a
~
u
i
∗
{\displaystyle {\tilde {a}}_{u_{i}}^{\ *}}
a
u
i
∗
{\displaystyle a_{u_{i}}^{\ *}}
a
~
u
i
∗
{\displaystyle {\tilde {a}}_{u_{i}}^{\ *}}
a
~
u
i
∗
{\displaystyle {\tilde {a}}_{u_{i}}^{\ *}}
A koordináták mint a bázivektorokra vett vetületek [ szerkesztés ] Egy
a
→
=
∑
j
=
1
n
a
u
j
e
→
u
j
{\displaystyle {\vec {a}}=\sum _{j=1}^{n}{a_{u_{j}}{\vec {e}}_{u_{j}}}}
a
u
i
{\displaystyle a_{u_{i}}}
e
→
u
i
∗
{\displaystyle {\vec {e}}_{u_{i}}^{\ *}}
e
→
i
{\displaystyle {\vec {e}}^{i}}
e
→
u
i
∗
⋅
a
→
=
∑
j
=
1
n
a
u
j
e
→
u
i
∗
⋅
e
→
u
j
=
∑
j
=
1
n
a
u
j
δ
i
j
=
a
u
i
{\displaystyle {\vec {e}}_{u_{i}}^{\ *}\cdot {\vec {a}}=\sum \limits _{j=1}^{n}{a_{u_{j}}{\vec {e}}_{u_{i}}^{\ *}\cdot {\vec {e}}_{u_{j}}}=\sum \limits _{j=1}^{n}{a_{u_{j}}\delta _{ij}}=a_{u_{i}}}
Ortonormális bázisvektorok esetén a ko- és kontravariáns bázisvektorok megegyezne, így a ko- és kontravariáns koordináták is.
Általában, egy tetszőleges vektor ábrázolható ko- és kontravariáns bázisban:
a
→
=
∑
i
=
1
n
a
u
i
b
→
u
i
=
∑
i
=
1
n
a
u
i
∗
b
→
u
i
∗
{\displaystyle {\vec {a}}=\sum \limits _{i=1}^{n}a_{u_{i}}{\vec {b}}_{u_{i}}=\sum \limits _{i=1}^{n}a_{u_{i}}^{\,*}{\vec {b}}_{u_{i}}^{\,*}}
Így a kontravariáns bázis a kovariáns koordinátákkal, és a kovariáns bázis a kontravariáns koordinátákkal kombinálódik. Ez a tulajdonság megőrzi a vektorokat a koordináta-rendszer megváltoztatásakor.
Mindkét oldalt megszorozva
b
→
u
j
{\displaystyle {\vec {b}}_{u_{j}}}
∑
i
=
1
n
a
u
i
b
→
u
i
⋅
b
→
u
j
⏟
g
i
j
=
∑
i
=
1
n
a
u
i
∗
b
→
u
i
∗
⋅
b
→
u
j
⏟
δ
i
j
⇒
a
u
j
∗
=
∑
i
=
1
n
g
i
j
a
u
i
⇒
a
u
i
=
∑
i
=
1
n
g
i
j
−
1
a
u
j
∗
{\displaystyle \sum \limits _{i=1}^{n}a_{u_{i}}\underbrace {{\vec {b}}_{u_{i}}\cdot {\vec {b}}_{u_{j}}} _{g_{ij}}=\sum \limits _{i=1}^{n}a_{u_{i}}^{\,*}\underbrace {{\vec {b}}_{u_{i}}^{\,*}\cdot {\vec {b}}_{u_{j}}} _{\delta _{ij}}\quad \Rightarrow \quad a_{u_{j}}^{\,*}=\sum \limits _{i=1}^{n}g_{ij}a_{u_{i}}\quad \Rightarrow \quad a_{u_{i}}=\sum \limits _{i=1}^{n}g_{ij}^{-1}a_{u_{j}}^{\,*}}
Így a
g
i
j
=
b
→
u
i
⋅
b
→
u
j
{\displaystyle g_{ij}={\vec {b}}_{u_{i}}\cdot {\vec {b}}_{u_{j}}}
g
i
j
−
1
=
b
→
u
i
∗
⋅
b
→
u
j
∗
{\displaystyle g_{ij}^{-1}={\vec {b}}_{u_{i}}^{\,*}\cdot {\vec {b}}_{u_{j}}^{\,*}}
a
u
i
{\displaystyle a_{u_{i}}}
a
u
j
∗
{\displaystyle a_{u_{j}}^{\,*}}
Ortogonális koordináták [ szerkesztés ] Ortogonális koordináta-rendszerekben egybeesnek a bázisvektorok és a duális bázisvektorok normáltjai. Ez a természetes bázisokra azt jelenti, hogy a megfelelő bázisvektorok párhuzamosak, és egy
h
u
i
2
{\displaystyle h_{u_{i}}^{2}}
e
→
u
i
∗
=
e
→
u
i
⟺
h
u
i
b
→
u
i
∗
=
1
h
u
i
b
→
u
i
≡
e
→
u
i
{\displaystyle {\vec {e}}_{u_{i}}^{\ *}={\vec {e}}_{u_{i}}\quad \iff \quad h_{u_{i}}{\vec {b}}_{u_{i}}^{\ *}={\frac {1}{h_{u_{i}}}}{\vec {b}}_{u_{i}}\equiv {\vec {e}}_{u_{i}}}
Normált bázisok esetén a koordináták megegyeznek:
a
u
i
∗
=
a
u
i
⟺
1
h
u
i
a
~
u
i
∗
=
h
u
i
a
~
u
i
≡
a
u
i
{\displaystyle a_{u_{i}}^{\ *}=a_{u_{i}}\quad \iff \quad {\frac {1}{h_{u_{i}}}}{\tilde {a}}_{u_{i}}^{\ *}=h_{u_{i}}{\tilde {a}}_{u_{i}}\equiv a_{u_{i}}}
Három dimenzióban a duális bázisvektorok kifejezhetők a bázisvektorok vektorszorzatát elosztva a bázisvektorok
det
(
e
→
u
1
,
e
→
u
2
,
e
→
u
3
)
{\displaystyle \det({\vec {e}}_{u_{1}},{\vec {e}}_{u_{2}},{\vec {e}}_{u_{3}})}
det
(
b
→
u
1
,
b
→
u
2
,
b
→
u
3
)
=
g
{\displaystyle \det({\vec {b}}_{u_{1}},{\vec {b}}_{u_{2}},{\vec {b}}_{u_{3}})={\sqrt {g}}}
e
→
u
1
∗
=
e
→
u
2
×
e
→
u
3
det
(
e
→
u
1
,
e
→
u
2
,
e
→
u
3
)
,
e
→
u
2
∗
=
e
→
u
3
×
e
→
u
1
det
(
e
→
u
1
,
e
→
u
2
,
e
→
u
3
)
,
e
→
u
3
∗
=
e
→
u
1
×
e
→
u
2
det
(
e
→
u
1
,
e
→
u
2
,
e
→
u
3
)
{\displaystyle {\vec {e}}_{u_{1}}^{\,*}={\frac {{\vec {e}}_{u_{2}}\times {\vec {e}}_{u_{3}}}{\det({\vec {e}}_{u_{1}},{\vec {e}}_{u_{2}},{\vec {e}}_{u_{3}})}}\ ,\quad \quad {\vec {e}}_{u_{2}}^{\,*}={\frac {{\vec {e}}_{u_{3}}\times {\vec {e}}_{u_{1}}}{\det({\vec {e}}_{u_{1}},{\vec {e}}_{u_{2}},{\vec {e}}_{u_{3}})}}\ ,\quad \quad {\vec {e}}_{u_{3}}^{\,*}={\frac {{\vec {e}}_{u_{1}}\times {\vec {e}}_{u_{2}}}{\det({\vec {e}}_{u_{1}},{\vec {e}}_{u_{2}},{\vec {e}}_{u_{3}})}}}
Kompaktabban, a normált bázisvektorokkal:
∑
k
=
1
3
ϵ
i
j
k
e
→
u
k
∗
=
e
→
u
i
×
e
→
u
j
det
(
e
→
u
1
,
e
→
u
2
,
e
→
u
3
)
{\displaystyle \sum _{k=1}^{3}\epsilon _{ijk}{\vec {e}}_{u_{k}}^{\,*}={\frac {{\vec {e}}_{u_{i}}\times {\vec {e}}_{u_{j}}}{\det({\vec {e}}_{u_{1}},{\vec {e}}_{u_{2}},{\vec {e}}_{u_{3}})}}}
és a természetes bázisvektorokkal:
∑
k
=
1
3
ϵ
i
j
k
b
→
u
k
∗
=
b
→
u
i
×
b
→
u
j
g
{\displaystyle \sum _{k=1}^{3}\epsilon _{ijk}{\vec {b}}_{u_{k}}^{\,*}={\frac {{\vec {b}}_{u_{i}}\times {\vec {b}}_{u_{j}}}{\sqrt {g}}}}
Míg a (kovariáns) bázisvektorok érintik a koordinátavonalakat, addig a (kontravariáns) duális bázis vektorai merőlegesek a koordinátafelületekre. Például, ha
e
→
u
2
{\displaystyle {\vec {e}}_{u_{2}}}
e
→
u
3
{\displaystyle {\vec {e}}_{u_{3}}}
e
→
u
1
∗
{\displaystyle {\vec {e}}_{u_{1}}^{\,*}}
Megfordítva, a kontravariáns bázisvektorokkal hasonlóan kifejezhetők a kovariáns bázisvektorok. Tehát a vektorszorzatot elosztjuk a
det
(
b
→
u
1
∗
,
b
→
u
2
∗
,
b
→
u
3
∗
)
=
1
/
g
{\displaystyle \det({\vec {b}}_{u_{1}}^{\ *},{\vec {b}}_{u_{2}}^{\ *},{\vec {b}}_{u_{3}}^{\ *})=1/{\sqrt {g}}}
det
(
e
→
u
1
∗
,
e
→
u
2
∗
,
e
→
u
3
∗
)
{\displaystyle \det({\vec {e}}_{u_{1}}^{\,*},{\vec {e}}_{u_{2}}^{\,*},{\vec {e}}_{u_{3}}^{\,*})}
∑
k
=
1
3
ϵ
i
j
k
e
→
u
k
=
e
→
u
i
∗
×
e
→
u
j
∗
det
(
e
→
u
1
∗
,
e
→
u
2
∗
,
e
→
u
3
∗
)
=
det
(
e
→
u
1
,
e
→
u
2
,
e
→
u
3
)
e
→
u
i
∗
×
e
→
u
j
∗
{\displaystyle \sum _{k=1}^{3}\epsilon _{ijk}{\vec {e}}_{u_{k}}={\frac {{\vec {e}}_{u_{i}}^{\,*}\times {\vec {e}}_{u_{j}}^{\,*}}{\det({\vec {e}}_{u_{1}}^{\,*},{\vec {e}}_{u_{2}}^{\,*},{\vec {e}}_{u_{3}}^{\,*})}}=\det({\vec {e}}_{u_{1}},{\vec {e}}_{u_{2}},{\vec {e}}_{u_{3}})\,{\vec {e}}_{u_{i}}^{\,*}\times {\vec {e}}_{u_{j}}^{\,*}}
∑
k
=
1
3
ϵ
i
j
k
b
→
u
k
=
b
→
u
i
∗
×
b
→
u
j
∗
det
(
b
→
u
1
∗
,
b
→
u
2
∗
,
b
→
u
3
∗
)
=
det
(
b
→
u
1
,
b
→
u
2
,
b
→
u
3
)
b
→
u
i
∗
×
b
→
u
j
∗
=
g
b
→
u
i
∗
×
b
→
u
j
∗
{\displaystyle \sum _{k=1}^{3}\epsilon _{ijk}{\vec {b}}_{u_{k}}={\frac {{\vec {b}}_{u_{i}}^{\ *}\times {\vec {b}}_{u_{j}}^{\ *}}{\det({\vec {b}}_{u_{1}}^{\ *},{\vec {b}}_{u_{2}}^{\ *},{\vec {b}}_{u_{3}}^{\ *})}}=\det({\vec {b}}_{u_{1}},{\vec {b}}_{u_{2}},{\vec {b}}_{u_{3}}){\vec {b}}_{u_{i}}^{\ *}\times {\vec {b}}_{u_{j}}^{\ *}={\sqrt {g}}\,{\vec {b}}_{u_{i}}^{\ *}\times {\vec {b}}_{u_{j}}^{\ *}}
Ha a kovariáns vektorok jobbsodrású bázist alkotnak, akkor a kontravariáns bázisvektorok is jobbsodratú koordináta-rendszert alkotnak. A két determináns szorzatának ugyanis egynek kell lennie.
Egy
n
{\displaystyle n}
tenzor kifejezhető
n
{\displaystyle n}
v
→
1
⊗
v
→
2
⊗
…
⊗
v
→
n
{\displaystyle {\vec {v}}_{1}\otimes {\vec {v}}_{2}\otimes \ldots \otimes {\vec {v}}_{n}}
A tenzorszorzás nem kommutatív, így a vektorok sorrendje nem cserélhető fel. Az
{
u
i
}
{\displaystyle \{u_{i}\}}
ϕ
:
R
n
→
R
{\displaystyle \phi :\mathbb {R} ^{n}\to \mathbb {R} }
koordinátatranszformáció során nem változtatnak értéket:
ϕ
(
u
i
)
=
ϕ
~
(
u
~
i
)
{\displaystyle \phi (u_{i})={\tilde {\phi }}({\tilde {u}}_{i})}
A vektorok kétfélék lehetnek, ko- és kontravariáns módon ábrázolhatók, ami
n
{\displaystyle n}
2
n
{\displaystyle 2^{n}}
Egy másodfokú tenzor négyféleképpen ábrázolható:
T
_
_
=
v
→
⊗
w
→
=
∑
i
,
j
=
1
n
v
u
i
w
u
j
b
→
u
i
∗
⊗
b
→
u
j
∗
=
∑
i
,
j
=
1
n
v
u
i
∗
w
u
j
∗
b
→
u
i
⊗
b
→
u
j
=
∑
i
,
j
=
1
n
v
u
i
w
u
j
∗
b
→
u
i
∗
⊗
b
→
u
j
=
∑
i
,
j
=
1
n
v
u
i
∗
w
u
j
b
→
u
i
⊗
b
→
u
j
∗
{\displaystyle {\underline {\underline {T}}}={\vec {v}}\otimes {\vec {w}}=\sum \limits _{i,j=1}^{n}v_{u_{i}}w_{u_{j}}{\vec {b}}_{u_{i}}^{\ *}\otimes {\vec {b}}_{u_{j}}^{\ *}=\sum \limits _{i,j=1}^{n}v_{u_{i}}^{\,*}w_{u_{j}}^{\,*}{\vec {b}}_{u_{i}}\otimes {\vec {b}}_{u_{j}}=\sum \limits _{i,j=1}^{n}v_{u_{i}}w_{u_{j}}^{\,*}{\vec {b}}_{u_{i}}^{\ *}\otimes {\vec {b}}_{u_{j}}=\sum \limits _{i,j=1}^{n}v_{u_{i}}^{\,*}w_{u_{j}}{\vec {b}}_{u_{i}}\otimes {\vec {b}}_{u_{j}}^{\ *}}
A négy eset: (tiszta) kontravariáns, (tiszta) kovariáns, kontra-kovaráns, ko-kovariáns.
Az egységtenzor, melyet az
I
_
_
⋅
v
→
=
v
→
{\displaystyle {\underline {\underline {I}}}\cdot {\vec {v}}={\vec {v}}}
I
_
_
=
∑
i
,
j
=
1
n
g
i
j
b
→
u
i
∗
⊗
b
→
u
j
∗
=
∑
i
,
j
=
1
n
g
i
j
b
→
u
i
⊗
b
→
u
j
=
∑
i
=
1
n
b
→
u
i
∗
⊗
b
→
u
i
=
∑
i
=
1
n
b
→
u
i
⊗
b
→
u
i
∗
{\displaystyle {\underline {\underline {I}}}=\sum \limits _{i,j=1}^{n}g_{ij}\,{\vec {b}}_{u_{i}}^{\ *}\otimes {\vec {b}}_{u_{j}}^{\ *}=\sum \limits _{i,j=1}^{n}g^{ij}\,{\vec {b}}_{u_{i}}\otimes {\vec {b}}_{u_{j}}=\sum \limits _{i=1}^{n}{\vec {b}}_{u_{i}}^{\ *}\otimes {\vec {b}}_{u_{i}}=\sum \limits _{i=1}^{n}{\vec {b}}_{u_{i}}\otimes {\vec {b}}_{u_{i}}^{\ *}}
Két vektor skalárszorzata:
v
→
⋅
w
→
=
∑
i
=
1
n
v
u
i
w
u
i
∗
=
∑
i
=
1
n
v
u
i
∗
w
u
i
=
∑
i
,
j
=
1
n
v
u
i
∗
g
i
j
w
u
j
∗
=
∑
i
,
j
=
1
n
v
u
i
g
i
j
w
u
j
{\displaystyle {\vec {v}}\cdot {\vec {w}}=\sum \limits _{i=1}^{n}v_{u_{i}}w_{u_{i}}^{\,*}=\sum \limits _{i=1}^{n}v_{u_{i}}^{\,*}w_{u_{i}}=\sum \limits _{i,j=1}^{n}v_{u_{i}}^{\,*}g^{ij}w_{u_{j}}^{\,*}=\sum \limits _{i,j=1}^{n}v_{u_{i}}g_{ij}w_{u_{j}}}
Ez megfelel a
v
→
⊗
w
→
{\displaystyle {\vec {v}}\otimes {\vec {w}}}
Egy harmadfokú tenzor nyolcféleképpen ábrázolható:
T
_
_
_
=
a
→
⊗
b
→
⊗
c
→
=
∑
i
,
j
,
k
=
1
n
a
u
i
b
u
j
c
u
k
b
→
u
i
∗
⊗
b
→
u
j
∗
⊗
b
→
u
k
∗
=
∑
i
,
j
,
k
=
1
n
a
u
i
b
u
j
c
u
k
∗
b
→
u
i
∗
⊗
b
→
u
j
∗
⊗
b
→
u
k
=
…
=
∑
i
,
j
,
k
=
1
n
a
u
i
∗
b
u
j
∗
c
u
k
∗
b
→
u
i
⊗
b
→
u
j
⊗
b
→
u
k
{\displaystyle {\underline {\underline {\underline {T}}}}={\vec {a}}\otimes {\vec {b}}\otimes {\vec {c}}=\sum \limits _{i,j,k=1}^{n}a_{u_{i}}b_{u_{j}}c_{u_{k}}{\vec {b}}_{u_{i}}^{\ *}\otimes {\vec {b}}_{u_{j}}^{\ *}\otimes {\vec {b}}_{u_{k}}^{\ *}=\sum \limits _{i,j,k=1}^{n}a_{u_{i}}b_{u_{j}}c_{u_{k}}^{\,*}{\vec {b}}_{u_{i}}^{\ *}\otimes {\vec {b}}_{u_{j}}^{\ *}\otimes {\vec {b}}_{u_{k}}=\ldots =\sum \limits _{i,j,k=1}^{n}a_{u_{i}}^{\,*}b_{u_{j}}^{\,*}c_{u_{k}}^{\,*}{\vec {b}}_{u_{i}}\otimes {\vec {b}}_{u_{j}}\otimes {\vec {b}}_{u_{k}}}
Három dimenzióban a teljesen antiszimmetrikus tenzor adódik, mint:
Az első reláció a Descartes-féle írásmód, a következő kettő pedig a görbe vonalú tenzorverzió leírásai közül kettő.
E
_
_
_
=
∑
i
,
j
,
k
=
1
n
ϵ
i
j
k
e
→
x
i
⊗
e
→
x
j
⊗
e
→
x
k
=
∑
i
,
j
,
k
=
1
n
E
i
j
k
b
→
u
i
∗
⊗
b
→
u
j
∗
⊗
b
→
u
k
∗
=
…
=
∑
i
,
j
,
k
=
1
n
E
i
j
k
b
→
u
i
⊗
b
→
u
j
⊗
b
→
u
k
{\displaystyle {\underline {\underline {\underline {\mathcal {E}}}}}=\sum \limits _{i,j,k=1}^{n}\epsilon _{ijk}{\vec {e}}_{x_{i}}\otimes {\vec {e}}_{x_{j}}\otimes {\vec {e}}_{x_{k}}=\sum \limits _{i,j,k=1}^{n}{\mathcal {E}}_{ijk}{\vec {b}}_{u_{i}}^{\ *}\otimes {\vec {b}}_{u_{j}}^{\ *}\otimes {\vec {b}}_{u_{k}}^{\ *}=\ldots =\sum \limits _{i,j,k=1}^{n}{\mathcal {E}}^{ijk}{\vec {b}}_{u_{i}}\otimes {\vec {b}}_{u_{j}}\otimes {\vec {b}}_{u_{k}}}
ϵ
i
j
k
=
det
[
e
→
x
i
,
e
→
x
j
,
e
→
x
k
]
≡
det
[
e
→
x
i
,
e
→
x
j
,
e
→
x
k
]
,
E
i
j
k
=
det
[
b
→
u
i
,
b
→
u
j
,
b
→
u
k
]
=
g
ϵ
i
j
k
,
E
i
j
k
=
det
[
b
→
u
i
∗
,
b
→
u
j
∗
,
b
→
u
k
∗
]
=
1
g
ϵ
i
j
k
{\displaystyle \epsilon _{ijk}=\det[{\vec {e}}_{x_{i}},{\vec {e}}_{x_{j}},{\vec {e}}_{x_{k}}]\equiv \det[{\vec {e}}_{x_{i}},{\vec {e}}_{x_{j}},{\vec {e}}_{x_{k}}]\ ,\quad {\mathcal {E}}_{ijk}=\det[{\vec {b}}_{u_{i}},{\vec {b}}_{u_{j}},{\vec {b}}_{u_{k}}]={\sqrt {g}}\,\epsilon _{ijk}\ ,\quad {\mathcal {E}}^{ijk}=\det[{\vec {b}}_{u_{i}}^{\ *},{\vec {b}}_{u_{j}}^{\ *},{\vec {b}}_{u_{k}}^{\ *}]={\frac {1}{\sqrt {g}}}\,\epsilon ^{ijk}}
A bázisvektorok deriváltjai [ szerkesztés ] A bázisvektorok deriváltjai görbe vonalú koordináta-rendszerekben a következőképpen különböznek a Descartes-féle koordináta-rendszerekben megszokottól. Mivel általában a koordinátagörbék nem egyenesek, és a bázisvektorok függenek a helytől, a bázisvektorokat is differenciálni kell. A szorzatszabályt alkalmazva:
∂
a
→
∂
u
k
=
∑
i
=
1
n
∂
(
a
u
i
e
→
u
i
)
∂
u
k
=
∑
i
=
1
n
[
∂
a
u
i
∂
u
k
e
→
u
i
+
a
u
i
∂
e
→
u
i
∂
u
k
]
{\displaystyle {\frac {\partial {\vec {a}}}{\partial u_{k}}}=\sum \limits _{i=1}^{n}{\frac {\partial \left(a_{u_{i}}{\vec {e}}_{u_{i}}\right)}{\partial u_{k}}}=\sum \limits _{i=1}^{n}{\left[{\frac {\partial a_{u_{i}}}{\partial u_{k}}}{\vec {e}}_{u_{i}}+a_{u_{i}}{\frac {\partial {\vec {e}}_{u_{i}}}{\partial u_{k}}}\right]}}
Illetve a természetes bázisban:
∂
a
→
∂
u
k
=
∑
i
=
1
n
∂
(
a
~
u
i
b
→
u
i
)
∂
u
k
=
∑
i
=
1
n
[
∂
a
~
u
i
∂
u
k
b
→
u
i
+
a
~
u
i
∂
b
→
u
i
∂
u
k
]
{\displaystyle {\frac {\partial {\vec {a}}}{\partial u_{k}}}=\sum \limits _{i=1}^{n}{\frac {\partial \left({\tilde {a}}_{u_{i}}{\vec {b}}_{u_{i}}\right)}{\partial u_{k}}}=\sum \limits _{i=1}^{n}{\left[{\frac {\partial {\tilde {a}}_{u_{i}}}{\partial u_{k}}}{\vec {b}}_{u_{i}}+{\tilde {a}}_{u_{i}}{\frac {\partial {\vec {b}}_{u_{i}}}{\partial u_{k}}}\right]}}
Christoffel-szimbólum [ szerkesztés ] Az
b
→
u
i
{\displaystyle {\vec {b}}_{u_{i}}}
u
k
{\displaystyle u_{k}}
{
b
→
u
j
|
j
=
1
,
2
,
…
,
n
}
{\displaystyle \{{\vec {b}}_{u_{j}}|j=1,2,\ldots ,n\}}
∂
b
→
u
i
∂
u
k
=
∑
j
=
1
n
Γ
k
i
j
b
→
u
j
{\displaystyle {\frac {\partial {\vec {b}}_{u_{i}}}{\partial u_{k}}}=\sum _{j=1}^{n}\Gamma _{ki}^{j}{\vec {b}}_{u_{j}}}
A
Γ
k
i
j
{\displaystyle \Gamma _{ki}^{j}}
Γ
k
i
j
=
b
→
u
j
∗
∂
b
→
u
i
∂
u
k
=
∑
l
g
j
l
b
→
u
l
∂
b
→
u
i
∂
u
k
=
∑
l
g
j
l
Γ
k
i
,
l
=
(
∇
u
j
)
⋅
∂
2
r
→
∂
u
k
∂
u
i
=
∑
l
∂
u
j
∂
x
l
∂
2
x
l
∂
u
k
∂
u
i
{\displaystyle \Gamma _{ki}^{j}={\vec {b}}_{u_{j}}^{\,*}{\frac {\partial {\vec {b}}_{u_{i}}}{\partial u_{k}}}=\sum _{l}g^{jl}{\vec {b}}_{u_{l}}^{\,}{\frac {\partial {\vec {b}}_{u_{i}}}{\partial u_{k}}}=\sum _{l}g^{jl}\Gamma _{ki,l}=(\nabla u_{j})\cdot {\frac {\partial ^{2}{\vec {r}}}{\partial u_{k}\partial u_{i}}}=\sum _{l}{\frac {\partial u_{j}}{\partial x_{l}}}{\frac {\partial ^{2}x_{l}}{\partial u_{k}\partial u_{i}}}}
A
Γ
k
i
,
l
{\displaystyle \Gamma _{ki,l}}
d
b
→
u
i
=
∑
j
,
k
=
1
n
Γ
k
i
j
b
→
u
j
d
u
k
{\displaystyle \mathrm {d} {\vec {b}}_{u_{i}}=\sum _{j,k=1}^{n}\Gamma _{ki}^{j}{\vec {b}}_{u_{j}}\mathrm {d} u_{k}}
Egy vektor deriváltja kifejezhető Christoffel-szimbólumokkal:
∂
a
→
∂
u
k
=
∑
i
=
1
n
[
∂
a
~
u
i
∂
u
k
b
→
u
i
+
∑
j
=
1
n
a
~
u
i
Γ
k
i
j
b
→
u
j
]
=
∑
i
=
1
n
[
∂
a
~
u
i
∂
u
k
+
∑
j
=
1
n
a
~
u
j
Γ
k
j
i
]
b
→
u
i
{\displaystyle {\frac {\partial {\vec {a}}}{\partial u_{k}}}=\sum \limits _{i=1}^{n}\left[{\frac {\partial {\tilde {a}}_{u_{i}}}{\partial u_{k}}}{\vec {b}}_{u_{i}}+\sum _{j=1}^{n}{\tilde {a}}_{u_{i}}\Gamma _{ki}^{j}{\vec {b}}_{u_{j}}\right]=\sum \limits _{i=1}^{n}\left[{\frac {\partial {\tilde {a}}_{u_{i}}}{\partial u_{k}}}+\sum _{j=1}^{n}{\tilde {a}}_{u_{j}}\Gamma _{kj}^{i}\right]{\vec {b}}_{u_{i}}}
Itt a második egyenlőségjelnél felcseréltük az
i
{\displaystyle i}
j
{\displaystyle j}
b
→
u
i
{\displaystyle {\vec {b}}_{u_{i}}}
Erre alapozható egy vektor kovariáns deriváltja:
∇
u
k
a
~
u
i
=
∂
a
~
u
i
∂
u
k
+
∑
j
=
1
n
a
~
u
j
Γ
k
j
i
{\displaystyle \nabla _{u_{k}}{\tilde {a}}_{u_{i}}={\frac {\partial {\tilde {a}}_{u_{i}}}{\partial u_{k}}}+\sum _{j=1}^{n}{\tilde {a}}_{u_{j}}\Gamma _{kj}^{i}}
Az első term az
a
→
{\displaystyle {\vec {a}}}
a
~
u
i
{\displaystyle {\tilde {a}}_{u_{i}}}
u
k
{\displaystyle u_{k}}
Christoffel-szimbólumok eltűnnek, és a kovariáns derivált megegyezik a parciális deriválttal.
A kovariáns derivált a sokaság geometriájának további geometriai szerkezetét tárja fel, ami lehetővé teszi különböző vektorterek és érintőterek vektorainak összehasonlítását. Így a kovariáns derivált különböző vektorterek differenciálgeometriai összefüggését állítja elő. Ez ahhoz szükséges például, hogy kiszámítsák egy
γ
→
(
t
)
{\displaystyle {\vec {\gamma }}(t)}
γ
→
′
(
t
+
Δ
t
)
{\displaystyle {\vec {\gamma }}^{\,\prime }(t+\Delta t)}
γ
→
′
(
t
)
{\displaystyle {\vec {\gamma }}^{\,\prime }(t)}
A metrikus tenzorok kovariáns deriváltjának koordinátái eltűnnek:
∇
u
k
g
i
j
=
∇
u
k
g
i
j
=
0
{\displaystyle \nabla _{u_{k}}g_{ij}=\nabla _{u_{k}}g^{ij}=0}
A kovariáns deriválttal általánosíthatók az irány szerinti deriváltak:
∇
w
→
a
→
=
∑
i
,
k
=
1
n
(
w
~
u
k
∂
a
~
u
i
∂
u
k
+
∑
j
=
1
n
w
~
u
k
a
~
u
j
Γ
k
j
i
)
b
→
u
i
{\displaystyle \nabla _{\vec {w}}{\vec {a}}=\sum _{i,k=1}^{n}\left({\tilde {w}}_{u_{k}}{\frac {\partial {\tilde {a}}_{u_{i}}}{\partial u_{k}}}+\sum _{j=1}^{n}{\tilde {w}}_{u_{k}}{\tilde {a}}_{u_{j}}\Gamma _{kj}^{i}\right){\vec {b}}_{u_{i}}}
Például ha egy görbe egy Riemann-sokaság geodetikus vonala , akkor definíció szerint két pont között a legrövidebb
γ
:
R
→
R
n
,
t
↦
r
→
(
t
)
{\displaystyle \gamma :\,\mathbb {R} \to \mathbb {R} ^{n},\,t\mapsto {\vec {r}}(t)}
∇
γ
˙
γ
˙
=
0
{\displaystyle \nabla _{\dot {\gamma }}{\dot {\gamma }}=0}
r
→
˙
{\displaystyle {\dot {\vec {r}}}}
γ
{\displaystyle \gamma }
R
n
{\displaystyle \mathbb {R} ^{n}}
∇
r
→
˙
r
→
˙
=
∑
i
,
k
=
1
n
(
d
u
k
d
t
⏟
u
˙
k
∂
u
˙
i
∂
u
k
+
∑
j
=
1
n
u
˙
k
u
˙
j
Γ
k
j
i
)
b
→
u
i
=
∑
i
=
1
n
(
d
u
˙
i
d
t
+
∑
j
,
k
=
1
n
u
˙
k
u
˙
j
Γ
k
j
i
)
b
→
u
i
{\displaystyle \nabla _{\dot {\vec {r}}}{\dot {\vec {r}}}=\sum _{i,k=1}^{n}{\Biggl (}\underbrace {\frac {\mathrm {d} u_{k}}{\mathrm {d} t}} _{{\dot {u}}_{k}}{\frac {\partial {\dot {u}}_{i}}{\partial u_{k}}}+\sum _{j=1}^{n}{\dot {u}}_{k}{\dot {u}}_{j}\Gamma _{kj}^{i}{\Biggr )}{\vec {b}}_{u_{i}}=\sum _{i=1}^{n}\left({\frac {\mathrm {d} {\dot {u}}_{i}}{\mathrm {d} t}}+\sum _{j,k=1}^{n}{\dot {u}}_{k}{\dot {u}}_{j}\Gamma _{kj}^{i}\right){\vec {b}}_{u_{i}}}
A Christoffel-szimbólumok a
∇
{\displaystyle \nabla }
Mivel a tekintetbe vett sokaságok (szemi)-Riemann-sokaságok (itt eltűnik a torziótenzor), azért a
∇
{\displaystyle \nabla }
∇
w
→
a
→
−
∇
a
→
w
→
{\displaystyle \nabla _{\vec {w}}{\vec {a}}-\nabla _{\vec {a}}{\vec {w}}}
L
w
→
a
→
≡
[
w
→
,
a
→
]
{\displaystyle L_{\vec {w}}{\vec {a}}\equiv [{\vec {w}},{\vec {a}}]}
∇
w
→
a
→
{\displaystyle \nabla _{\vec {w}}{\vec {a}}}
w
→
{\displaystyle {\vec {w}}}
L
w
→
a
→
{\displaystyle L_{\vec {w}}{\vec {a}}}
A Christoffel-szimbólumok tulajdonságai [ szerkesztés ] Schwarz tétele, illetve a
∇
{\displaystyle \nabla }
∂
b
→
u
i
∂
u
j
=
∂
2
r
→
∂
u
j
∂
u
i
=
∂
2
r
→
∂
u
i
∂
u
j
=
∂
b
→
u
j
∂
u
i
⟹
Γ
i
j
k
=
Γ
j
i
k
{\displaystyle {\frac {\partial {\vec {b}}_{u_{i}}}{\partial u_{j}}}={\frac {\partial ^{2}{\vec {r}}}{\partial u_{j}\partial u_{i}}}={\frac {\partial ^{2}{\vec {r}}}{\partial u_{i}\partial u_{j}}}={\frac {\partial {\vec {b}}_{u_{j}}}{\partial u_{i}}}\quad \Longrightarrow \quad \Gamma _{ij}^{k}=\Gamma _{ji}^{k}}
Ez alapján a Christoffel-szimbólumok a
g
i
j
{\displaystyle g_{ij}}
metrikus együtthatók alapján:
Γ
k
i
,
l
=
1
2
(
∂
g
i
l
∂
u
k
+
∂
g
k
l
∂
u
i
−
∂
g
k
i
∂
u
l
)
⟹
Γ
k
i
j
=
∑
l
=
1
n
g
j
l
2
(
∂
g
i
l
∂
u
k
+
∂
g
k
l
∂
u
i
−
∂
g
k
i
∂
u
l
)
{\displaystyle \Gamma _{ki,l}={\frac {1}{2}}\left({\frac {\partial g_{il}}{\partial u_{k}}}+{\frac {\partial g_{kl}}{\partial u_{i}}}-{\frac {\partial g_{ki}}{\partial u_{l}}}\right)\quad \Longrightarrow \quad \Gamma _{ki}^{j}=\sum _{l=1}^{n}{\frac {g^{jl}}{2}}\left({\frac {\partial g_{il}}{\partial u_{k}}}+{\frac {\partial g_{kl}}{\partial u_{i}}}-{\frac {\partial g_{ki}}{\partial u_{l}}}\right)}
Ez következik abból a relációból, hogy:
∂
g
i
j
∂
u
k
=
∂
(
b
→
u
i
⋅
b
→
u
j
)
∂
u
k
=
∂
b
→
u
i
∂
u
k
⋅
b
→
u
j
+
b
→
u
i
⋅
∂
b
→
u
j
∂
u
k
=
∑
l
Γ
i
k
l
b
→
u
l
⋅
b
→
u
j
+
∑
l
Γ
j
k
l
b
→
u
i
⋅
b
→
u
l
=
∑
l
Γ
i
k
l
g
j
l
+
∑
l
Γ
j
k
l
g
i
l
=
Γ
i
k
,
j
+
Γ
j
k
,
i
{\displaystyle {\frac {\partial g_{ij}}{\partial u_{k}}}={\frac {\partial ({\vec {b}}_{u_{i}}\cdot {\vec {b}}_{u_{j}})}{\partial u_{k}}}={\frac {\partial {\vec {b}}_{u_{i}}}{\partial u_{k}}}\cdot {\vec {b}}_{u_{j}}+{\vec {b}}_{u_{i}}\cdot {\frac {\partial {\vec {b}}_{u_{j}}}{\partial u_{k}}}=\sum _{l}\Gamma _{ik}^{l}{\vec {b}}_{u_{l}}\cdot {\vec {b}}_{u_{j}}+\sum _{l}\Gamma _{jk}^{l}{\vec {b}}_{u_{i}}\cdot {\vec {b}}_{u_{l}}=\sum _{l}\Gamma _{ik}^{l}g_{jl}+\sum _{l}\Gamma _{jk}^{l}g_{il}=\Gamma _{ik,j}+\Gamma _{jk,i}}
és
∂
k
g
i
j
{\displaystyle \partial _{k}g_{ij}}
∂
i
g
j
k
{\displaystyle \partial _{i}g_{jk}}
∂
j
g
k
i
{\displaystyle \partial _{j}g_{ki}}
A duális bázisvektorok deriváltjára a következő összefüggést kapjuk:
Γ
k
i
j
=
b
→
u
j
∗
⋅
∂
b
→
u
i
∂
u
k
=
∂
∂
u
k
b
→
u
j
∗
⋅
b
→
u
i
⏞
δ
i
j
⏟
0
−
∂
b
→
u
j
∗
∂
u
k
⋅
b
→
u
i
=
−
∂
b
→
u
j
∗
∂
u
k
⋅
b
→
u
i
⟹
∂
b
→
u
j
∗
∂
u
k
=
−
Γ
k
i
j
b
→
u
i
∗
{\displaystyle \Gamma _{ki}^{j}={\vec {b}}_{u_{j}}^{\,*}\cdot {\frac {\partial {\vec {b}}_{u_{i}}}{\partial u_{k}}}=\underbrace {{\frac {\partial }{\partial u_{k}}}\overbrace {{\vec {b}}_{u_{j}}^{\,*}\cdot {\vec {b}}_{u_{i}}} ^{\delta _{ij}}} _{0}-{\frac {\partial {\vec {b}}_{u_{j}}^{\,*}}{\partial u_{k}}}\cdot {\vec {b}}_{u_{i}}=-{\frac {\partial {\vec {b}}_{u_{j}}^{\,*}}{\partial u_{k}}}\cdot {\vec {b}}_{u_{i}}\quad \Longrightarrow \quad {\frac {\partial {\vec {b}}_{u_{j}}^{\,*}}{\partial u_{k}}}=-\Gamma _{ki}^{j}{\vec {b}}_{u_{i}}^{\,*}}
Ez alapján a kovariáns komponensek kovariáns deriváltjai:
∂
a
→
∂
u
k
=
∑
i
=
1
n
∂
(
a
~
u
i
∗
b
→
u
i
∗
)
∂
u
k
=
∑
i
=
1
n
[
∂
a
~
u
i
∗
∂
u
k
−
∑
j
a
~
u
j
∗
Γ
k
i
j
]
b
→
u
i
∗
⟹
∇
u
k
a
~
u
i
∗
=
∂
a
~
u
i
∗
∂
u
k
−
∑
j
=
1
n
a
~
u
j
∗
Γ
k
i
j
{\displaystyle {\frac {\partial {\vec {a}}}{\partial u_{k}}}=\sum \limits _{i=1}^{n}{\frac {\partial \left({\tilde {a}}_{u_{i}}^{\,*}{\vec {b}}_{u_{i}}^{\ *}\right)}{\partial u_{k}}}=\sum \limits _{i=1}^{n}\left[{\frac {\partial {\tilde {a}}_{u_{i}}^{\,*}}{\partial u_{k}}}-\sum _{j}{\tilde {a}}_{u_{j}}^{\,*}\Gamma _{ki}^{j}\right]{\vec {b}}_{u_{i}}^{\,*}\quad \Longrightarrow \quad \nabla _{u_{k}}{\tilde {a}}_{u_{i}}^{\,*}={\frac {\partial {\tilde {a}}_{u_{i}}^{\,*}}{\partial u_{k}}}-\sum _{j=1}^{n}{\tilde {a}}_{u_{j}}^{\,*}\Gamma _{ki}^{j}}
Fontos megjegyezni, hogy a Christoffel-szimbólumok három indexükkel nem írnak le harmadfokú tenzort, mivel nem mutatják a tenzoroknál megkövetelt viselkedést a transzformációkkal szemben:
Γ
¯
i
j
k
:=
∑
l
,
m
,
n
∂
u
¯
k
∂
u
l
∂
u
m
∂
u
¯
i
∂
u
n
∂
u
¯
j
Γ
m
n
l
+
∑
n
∂
u
¯
k
∂
u
n
∂
2
u
n
∂
u
¯
i
∂
u
¯
j
{\displaystyle {\bar {\Gamma }}_{ij}^{k}:=\sum _{l,m,n}{\frac {\partial {\bar {u}}_{k}}{\partial u_{l}}}{\frac {\partial u_{m}}{\partial {\bar {u}}_{i}}}{\frac {\partial u_{n}}{\partial {\bar {u}}_{j}}}\Gamma _{mn}^{l}+\sum _{n}{\frac {\partial {\bar {u}}_{k}}{\partial u_{n}}}{\frac {\partial ^{2}u_{n}}{\partial {\bar {u}}_{i}\partial {\bar {u}}_{j}}}}
A transzformációs formulában szereplő második tag miatt nincs szó tenzorról. Emiatt a Christoffel-szimbólumokat jelölik úgy is, hogy ne lehessen tenzornak nézni őket:
Γ
i
j
k
=
{
k
i
j
}
illetve
Γ
i
j
,
k
=
[
i
j
,
k
]
{\displaystyle \Gamma _{ij}^{k}=\left\{{\begin{array}{c}k\\ij\end{array}}\right\}\quad {\text{illetve}}\quad \Gamma _{ij,k}=\left[ij,k\right]}
A transzformációval szembeni viselkedésről tett kijelentés általánosítható: Egy tenzor parciális deriváltjának indexe (
i
{\displaystyle i}
∂
i
A
{\displaystyle \partial _{i}A}
∂
i
∂
j
A
{\displaystyle \partial _{i}\partial _{j}A}
i
,
j
{\displaystyle i,j}
n
{\displaystyle n}
∇
i
∇
j
A
{\displaystyle \nabla _{i}\nabla _{j}A}
i
{\displaystyle i}
j
{\displaystyle j}
Görbe vonalú koordináták három dimenzióban [ szerkesztés ] Vektorszorzat és alternáló tenzor [ szerkesztés ] Descartes-koordinátákban a vektorszorzás az
ϵ
i
j
k
{\displaystyle \epsilon ^{ijk}}
v
→
×
w
→
=
∑
i
j
k
ϵ
i
j
k
v
j
w
k
e
→
i
∗
=
∑
i
j
k
ϵ
i
j
k
v
j
∗
w
k
∗
e
→
i
ahol
ϵ
i
j
k
=
ϵ
i
j
k
=
det
[
e
→
i
,
e
→
j
,
e
→
k
]
{\displaystyle {\vec {v}}\times {\vec {w}}=\sum _{ijk}\epsilon _{ijk}v_{j}w_{k}{\vec {e}}_{i}^{\,*}=\sum _{ijk}\epsilon ^{ijk}v_{j}^{\,*}w_{k}^{\,*}{\vec {e}}_{i}\quad {\text{ahol}}\quad \epsilon _{ijk}=\epsilon ^{ijk}=\det[{\vec {e}}_{i},{\vec {e}}_{j},{\vec {e}}_{k}]}
Görbe vonalú
{
u
i
}
{\displaystyle \{u_{i}\}}
E
i
j
k
=
det
[
b
→
u
i
,
b
→
u
j
,
b
→
u
k
]
=
g
ϵ
i
j
k
,
E
i
j
k
=
det
[
b
→
u
i
∗
,
b
→
u
j
∗
,
b
→
u
k
∗
]
=
1
g
ϵ
i
j
k
{\displaystyle {\mathcal {E}}_{ijk}=\det[{\vec {b}}_{u_{i}},{\vec {b}}_{u_{j}},{\vec {b}}_{u_{k}}]={\sqrt {g}}\,\epsilon _{ijk}\ ,\quad {\mathcal {E}}^{ijk}=\det[{\vec {b}}_{u_{i}}^{\ *},{\vec {b}}_{u_{j}}^{\ *},{\vec {b}}_{u_{k}}^{\ *}]={\frac {1}{\sqrt {g}}}\,\epsilon ^{ijk}}
alternáló tenzor használható:
v
→
×
w
→
=
∑
i
j
k
E
i
j
k
v
~
u
j
w
~
u
k
b
→
u
i
∗
=
∑
i
j
k
E
i
j
k
v
~
u
j
∗
w
~
u
k
∗
b
→
u
i
=
g
|
b
→
u
1
∗
b
→
u
2
∗
b
→
u
3
∗
v
~
u
1
v
~
u
2
v
~
u
3
w
~
u
1
w
~
u
2
w
~
u
3
|
=
1
g
|
b
→
u
1
b
→
u
2
b
→
u
3
v
~
u
1
∗
v
~
u
2
∗
v
~
u
3
∗
w
~
u
1
∗
w
~
u
2
∗
w
~
u
3
∗
|
{\displaystyle {\begin{aligned}{\vec {v}}\times {\vec {w}}&=\sum _{ijk}{\mathcal {E}}_{ijk}{\tilde {v}}_{u_{j}}{\tilde {w}}_{u_{k}}{\vec {b}}_{u_{i}}^{\,*}=\sum _{ijk}{\mathcal {E}}^{ijk}{\tilde {v}}_{u_{j}}^{\,*}{\tilde {w}}_{u_{k}}^{\,*}{\vec {b}}_{u_{i}}\\&={\sqrt {g}}\left|{\begin{matrix}{\vec {b}}_{u_{1}}^{\ *}&{\vec {b}}_{u_{2}}^{\ *}&{\vec {b}}_{u_{3}}^{\ *}\\{\tilde {v}}_{u_{1}}&{\tilde {v}}_{u_{2}}&{\tilde {v}}_{u_{3}}\\{\tilde {w}}_{u_{1}}&{\tilde {w}}_{u_{2}}&{\tilde {w}}_{u_{3}}\end{matrix}}\right|={\frac {1}{\sqrt {g}}}\left|{\begin{matrix}{\vec {b}}_{u_{1}}&{\vec {b}}_{u_{2}}&{\vec {b}}_{u_{3}}\\{\tilde {v}}_{u_{1}}^{\,*}&{\tilde {v}}_{u_{2}}^{\,*}&{\tilde {v}}_{u_{3}}^{\,*}\\{\tilde {w}}_{u_{1}}^{\,*}&{\tilde {w}}_{u_{2}}^{\,*}&{\tilde {w}}_{u_{3}}^{\,*}\end{matrix}}\right|\end{aligned}}}
Ez levezethető abból, hogy
b
→
u
j
×
b
→
u
k
=
∑
i
g
ϵ
i
j
k
b
→
u
i
∗
{\displaystyle {\vec {b}}_{u_{j}}\times {\vec {b}}_{u_{k}}=\sum _{i}{\sqrt {g}}\,\epsilon _{ijk}{\vec {b}}_{u_{i}}^{\,*}}
E
i
j
k
:=
(
b
→
u
j
×
b
→
u
k
)
⋅
b
→
u
i
=
∑
l
g
ϵ
l
j
k
b
→
u
l
∗
⋅
b
→
u
i
⏟
δ
l
,
i
=
g
ϵ
i
j
k
{\displaystyle {\mathcal {E}}_{ijk}:=\left({\vec {b}}_{u_{j}}\times {\vec {b}}_{u_{k}}\right)\cdot {\vec {b}}_{u_{i}}=\sum _{l}{\sqrt {g}}\,\epsilon _{ljk}\underbrace {{\vec {b}}_{u_{l}}^{\,*}\cdot {\vec {b}}_{u_{i}}} _{\delta _{l,i}}={\sqrt {g}}\,\epsilon _{ijk}}
v
→
×
w
→
=
∑
j
k
(
v
~
u
j
b
→
u
j
)
×
(
w
~
u
k
b
→
u
k
)
=
∑
j
k
v
~
u
j
w
~
u
k
(
b
→
u
j
×
b
→
u
k
)
=
∑
i
j
k
v
~
u
j
w
~
u
k
g
ϵ
i
j
k
⏟
E
i
j
k
b
→
u
i
∗
{\displaystyle {\vec {v}}\times {\vec {w}}=\sum _{jk}\left({\tilde {v}}_{u_{j}}{\vec {b}}_{u_{j}}\right)\times \left({\tilde {w}}_{u_{k}}{\vec {b}}_{u_{k}}\right)=\sum _{jk}{\tilde {v}}_{u_{j}}{\tilde {w}}_{u_{k}}\left({\vec {b}}_{u_{j}}\times {\vec {b}}_{u_{k}}\right)=\sum _{ijk}{\tilde {v}}_{u_{j}}{\tilde {w}}_{u_{k}}\underbrace {{\sqrt {g}}\,\epsilon _{ijk}} _{{\mathcal {E}}_{ijk}}{\vec {b}}_{u_{i}}^{\,*}}
A következő számításból látható, hogy
E
i
j
k
{\displaystyle {\mathcal {E}}_{ijk}}
E
i
j
k
:=
det
[
∂
r
→
∂
u
i
,
∂
r
→
∂
u
j
,
∂
r
→
∂
u
k
]
=
det
[
∑
l
∂
x
l
∂
u
i
∂
r
→
∂
x
l
⏟
e
→
l
,
∑
m
∂
x
m
∂
u
j
∂
r
→
∂
x
m
⏟
e
→
m
,
∑
n
∂
x
n
∂
u
k
∂
r
→
∂
x
n
⏟
e
→
n
]
=
∑
l
,
m
,
n
∂
x
l
∂
u
i
∂
x
m
∂
u
j
∂
x
n
∂
u
k
det
[
e
→
l
,
e
→
m
,
e
→
n
]
⏟
ϵ
l
m
n
{\displaystyle {\begin{aligned}{\mathcal {E}}_{ijk}:=\det \!\left[{\frac {\partial {\vec {r}}}{\partial u_{i}}},{\frac {\partial {\vec {r}}}{\partial u_{j}}},{\frac {\partial {\vec {r}}}{\partial u_{k}}}\right]&=\det \!{\Biggl [}\sum _{l}{\frac {\partial x_{l}}{\partial u_{i}}}\underbrace {\frac {\partial {\vec {r}}}{\partial x_{l}}} _{{\vec {e}}_{l}},\sum _{m}{\frac {\partial x_{m}}{\partial u_{j}}}\underbrace {\frac {\partial {\vec {r}}}{\partial x_{m}}} _{{\vec {e}}_{m}},\sum _{n}{\frac {\partial x_{n}}{\partial u_{k}}}\underbrace {\frac {\partial {\vec {r}}}{\partial x_{n}}} _{{\vec {e}}_{n}}{\Biggr ]}\\&=\sum _{l,m,n}{\frac {\partial x_{l}}{\partial u_{i}}}{\frac {\partial x_{m}}{\partial u_{j}}}{\frac {\partial x_{n}}{\partial u_{k}}}\underbrace {\det \!\left[{\vec {e}}_{l},{\vec {e}}_{m},{\vec {e}}_{n}\right]} _{\epsilon _{lmn}}\end{aligned}}}
A vektorszorzat a normált bázisban:
v
→
×
w
→
=
∑
i
j
k
E
i
j
k
v
u
j
w
u
k
e
→
u
i
∗
h
u
j
h
u
k
h
u
i
=
∑
i
j
k
E
i
j
k
h
u
j
v
u
j
∗
h
u
k
w
u
k
∗
h
u
i
e
→
u
i
=
g
|
h
u
1
−
1
e
→
u
1
∗
h
u
2
−
1
e
→
u
2
∗
h
u
3
−
1
e
→
u
3
∗
h
u
1
−
1
v
u
1
h
u
2
−
1
v
u
2
h
u
3
−
1
v
u
3
h
u
1
−
1
w
u
1
h
u
2
−
1
w
u
2
h
u
3
−
1
w
u
3
|
=
1
g
|
h
u
1
e
→
u
1
h
u
2
e
→
u
2
h
u
3
e
→
u
3
h
u
1
v
u
1
∗
h
u
2
v
u
2
∗
h
u
3
v
u
3
∗
h
u
1
w
u
1
∗
h
u
2
w
u
2
∗
h
u
3
w
u
3
∗
|
{\displaystyle {\begin{aligned}{\vec {v}}\times {\vec {w}}&=\sum _{ijk}{\mathcal {E}}_{ijk}{\frac {v_{u_{j}}w_{u_{k}}{\vec {e}}_{u_{i}}^{\,*}}{h_{u_{j}}h_{u_{k}}h_{u_{i}}}}=\sum _{ijk}{\mathcal {E}}^{ijk}h_{u_{j}}v_{u_{j}}^{\,*}h_{u_{k}}w_{u_{k}}^{\,*}h_{u_{i}}{\vec {e}}_{u_{i}}\\&={\sqrt {g}}\left|{\begin{matrix}h_{u_{1}}^{-1}{\vec {e}}_{u_{1}}^{\ *}&h_{u_{2}}^{-1}{\vec {e}}_{u_{2}}^{\ *}&h_{u_{3}}^{-1}{\vec {e}}_{u_{3}}^{\ *}\\h_{u_{1}}^{-1}v_{u_{1}}&h_{u_{2}}^{-1}v_{u_{2}}&h_{u_{3}}^{-1}v_{u_{3}}\\h_{u_{1}}^{-1}w_{u_{1}}&h_{u_{2}}^{-1}w_{u_{2}}&h_{u_{3}}^{-1}w_{u_{3}}\end{matrix}}\right|={\frac {1}{\sqrt {g}}}\left|{\begin{matrix}h_{u_{1}}{\vec {e}}_{u_{1}}&h_{u_{2}}{\vec {e}}_{u_{2}}&h_{u_{3}}{\vec {e}}_{u_{3}}\\h_{u_{1}}v_{u_{1}}^{\,*}&h_{u_{2}}v_{u_{2}}^{\,*}&h_{u_{3}}v_{u_{3}}^{\,*}\\h_{u_{1}}w_{u_{1}}^{\,*}&h_{u_{2}}w_{u_{2}}^{\,*}&h_{u_{3}}w_{u_{3}}^{\,*}\end{matrix}}\right|\end{aligned}}}
Koordinátafelületek: belső geometria [ szerkesztés ] Az általánosság megszorítás nélkül feltesszük, hogy az
u
3
=
const
{\displaystyle u_{3}={\text{const}}}
b
→
u
3
∗
{\displaystyle {\vec {b}}_{u_{3}}^{\,*}}
n
→
=
b
→
u
1
×
b
→
u
2
=
g
b
→
u
3
∗
{\displaystyle {\vec {n}}={\vec {b}}_{u_{1}}\times {\vec {b}}_{u_{2}}={\sqrt {g}}\,{\vec {b}}_{u_{3}}^{\,*}}
Konvenció szerint
R
3
{\displaystyle \mathbb {R} ^{3}}
első alapforma ):
E
=
(
∂
r
→
∂
u
1
)
2
=
b
→
u
1
2
=
h
u
1
2
=
g
11
{\displaystyle E=\left({\frac {\partial {\vec {r}}}{\partial u_{1}}}\right)^{2}={\vec {b}}_{u_{1}}^{\ 2}=h_{u_{1}}^{2}=g_{11}}
F
=
∂
r
→
∂
u
1
⋅
∂
r
→
∂
u
2
=
b
→
u
1
⋅
b
→
u
2
=
h
u
1
h
u
2
e
→
u
1
⋅
e
→
u
2
=
g
12
{\displaystyle F={\frac {\partial {\vec {r}}}{\partial u_{1}}}\cdot {\frac {\partial {\vec {r}}}{\partial u_{2}}}={\vec {b}}_{u_{1}}\cdot {\vec {b}}_{u_{2}}=h_{u_{1}}h_{u_{2}}{\vec {e}}_{u_{1}}\cdot {\vec {e}}_{u_{2}}=g_{12}}
G
=
(
∂
r
→
∂
u
2
)
2
=
b
→
u
2
2
=
h
u
2
2
=
g
22
{\displaystyle G=\left({\frac {\partial {\vec {r}}}{\partial u_{2}}}\right)^{2}={\vec {b}}_{u_{2}}^{\ 2}=h_{u_{2}}^{2}=g_{22}}
Ortogonális koordinátákban
e
→
u
i
⋅
e
→
u
j
=
δ
i
j
{\displaystyle {\vec {e}}_{u_{i}}\cdot {\vec {e}}_{u_{j}}=\delta _{ij}}
F
=
0
{\displaystyle F=0}
A felület metrikus tenzora és ennek Gram-determinánsa:
g
~
_
_
=
(
E
F
F
G
)
⇒
g
~
=
det
g
~
_
_
=
E
G
−
F
2
=
b
→
u
1
2
b
→
u
2
2
−
(
b
→
u
1
⋅
b
→
u
2
)
2
=
(
b
→
u
1
×
b
→
u
2
)
2
{\displaystyle {\underline {\underline {\tilde {g}}}}=\left({\begin{array}{cc}E&F\\F&G\end{array}}\right)\quad \Rightarrow \quad {\tilde {g}}=\det {\underline {\underline {\tilde {g}}}}=EG-F^{2}={\vec {b}}_{u_{1}}^{\ 2}{\vec {b}}_{u_{2}}^{\ 2}-({\vec {b}}_{u_{1}}\cdot {\vec {b}}_{u_{2}})^{2}=({\vec {b}}_{u_{1}}\times {\vec {b}}_{u_{2}})^{2}}
A felület funkcionáldeterminánsa:
g
~
=
E
G
−
F
2
=
|
b
→
u
1
×
b
→
u
2
|
=
det
[
b
→
u
1
,
b
→
u
2
,
n
^
]
{\displaystyle {\sqrt {\tilde {g}}}={\sqrt {EG-F^{2}}}=\left|{\vec {b}}_{u_{1}}\times {\vec {b}}_{u_{2}}\right|=\det \left[{\vec {b}}_{u_{1}},{\vec {b}}_{u_{2}},{\hat {n}}\right]}
ahol
n
^
=
n
→
/
|
n
→
|
{\displaystyle {\hat {n}}={\vec {n}}/|{\vec {n}}|}
Az inverz metrikus tenzor:
g
~
_
_
−
1
=
1
g
~
(
G
−
F
−
F
E
)
{\displaystyle {\underline {\underline {\tilde {g}}}}^{-1}={\frac {1}{\tilde {g}}}\left({\begin{array}{cc}G&-F\\-F&E\end{array}}\right)}
Koordinátafelületek: Külső geometria [ szerkesztés ] A következőkben a görög betűs indexek az 1,2 értékeket veszik fel, és a felület koordinátáit és bázisvektorait jelölik.
A
n
^
{\displaystyle {\hat {n}}}
u
β
{\displaystyle u_{\beta }}
parciális deriváltja előállítható a
e
→
α
{\displaystyle {\vec {e}}_{\alpha }}
n
^
⋅
n
^
=
1
{\displaystyle {\hat {n}}\cdot {\hat {n}}=1}
n
^
⋅
∂
β
n
^
=
0
{\displaystyle {\hat {n}}\cdot \partial _{\beta }{\hat {n}}=0}
∂
β
n
^
{\displaystyle \partial _{\beta }{\hat {n}}}
n
^
{\displaystyle {\hat {n}}}
h
{\displaystyle h}
∂
β
n
^
=
−
∑
α
=
1
2
h
β
α
e
→
α
=
−
∑
α
=
1
2
h
α
β
e
→
α
∗
{\displaystyle \partial _{\beta }{\hat {n}}=-\sum _{\alpha =1}^{2}h_{\ \beta }^{\alpha }{\vec {e}}_{\alpha }=-\sum _{\alpha =1}^{2}h_{\alpha \beta }{\vec {e}}_{\alpha }^{\ *}}
A szakirodalom a
h
{\displaystyle h}
h
α
β
{\displaystyle h_{\alpha \beta }}
h
α
β
=
−
e
→
α
⋅
∂
β
n
^
=
−
∂
β
(
e
→
α
⋅
n
^
)
⏟
=
0
+
n
^
⋅
∂
β
e
→
α
=
n
^
⋅
∂
β
e
→
α
=
1
g
~
det
[
b
→
u
1
,
b
→
u
2
,
∂
β
e
→
α
]
{\displaystyle h_{\alpha \beta }=-{\vec {e}}_{\alpha }\cdot \partial _{\beta }{\hat {n}}=-\partial _{\beta }\underbrace {({\vec {e}}_{\alpha }\cdot {\hat {n}})} _{=0}+{\hat {n}}\cdot \partial _{\beta }{\vec {e}}_{\alpha }={\hat {n}}\cdot \partial _{\beta }{\vec {e}}_{\alpha }={\frac {1}{\sqrt {{\tilde {g}}^{\,}}}}\det \left[{\vec {b}}_{u_{1}},{\vec {b}}_{u_{2}},\partial _{\beta }{\vec {e}}_{\alpha }\right]}
ahol
n
^
=
(
b
→
u
1
×
b
→
u
2
)
/
g
~
{\displaystyle {\hat {n}}=\left({\vec {b}}_{u_{1}}\times {\vec {b}}_{u_{2}}\right)/{\sqrt {\tilde {g}}}}
h
α
β
=
n
^
⋅
∂
2
r
→
∂
u
β
∂
u
α
=
∑
i
,
j
,
k
=
1
3
1
g
~
ϵ
i
j
k
∂
x
i
∂
u
1
∂
x
j
∂
u
1
∂
2
x
k
∂
u
β
∂
u
α
=:
(
L
M
M
N
)
α
β
{\displaystyle h_{\alpha \beta }={\hat {n}}\cdot {\frac {\partial ^{2}{\vec {r}}}{\partial u_{\beta }\partial u_{\alpha }}}=\sum _{i,j,k=1}^{3}{\frac {1}{\sqrt {{\tilde {g}}^{\,}}}}\epsilon _{ijk}{\frac {\partial x_{i}}{\partial u_{1}}}{\frac {\partial x_{j}}{\partial u_{1}}}{\frac {\partial ^{2}x_{k}}{\partial u_{\beta }\partial u_{\alpha }}}=:\left({\begin{array}{cc}L&M\\M&N\end{array}}\right)_{\alpha \beta }}
lásd második alapforma .
A
h
α
β
{\displaystyle h_{\alpha \beta }}
n
^
=
e
→
3
∗
{\displaystyle {\hat {n}}={\vec {e}}_{3}^{\ *}}
h
α
β
=
n
^
⋅
∂
β
e
→
α
=
n
^
⋅
∑
i
=
1
3
e
→
i
Γ
α
β
i
=
∑
i
=
1
3
e
→
3
∗
⋅
e
→
i
⏟
δ
i
3
Γ
α
β
i
=
Γ
α
β
3
{\displaystyle h_{\alpha \beta }={\hat {n}}\cdot \partial _{\beta }{\vec {e}}_{\alpha }={\hat {n}}\cdot \sum _{i=1}^{3}{\vec {e}}_{i}\Gamma _{\alpha \beta }^{i}=\sum _{i=1}^{3}\underbrace {{\vec {e}}_{3}^{\ *}\cdot {\vec {e}}_{i}} _{\delta _{i}^{3}}\Gamma _{\alpha \beta }^{i}=\Gamma _{\alpha \beta }^{3}}
Innen a Gauß-Weingarten-egyenletek :
∂
β
e
→
α
=
∑
γ
=
1
2
Γ
α
β
γ
e
→
γ
+
h
α
β
n
^
,
∂
β
n
^
=
−
∑
γ
=
1
2
h
β
γ
e
→
γ
{\displaystyle \partial _{\beta }{\vec {e}}_{\alpha }=\sum _{\gamma =1}^{2}\Gamma _{\alpha \beta }^{\gamma }{\vec {e}}_{\gamma }+h_{\alpha \beta }{\hat {n}}\ ,\quad \partial _{\beta }{\hat {n}}=-\sum _{\gamma =1}^{2}h_{\ \beta }^{\gamma }{\vec {e}}_{\gamma }}
A második alapforma függ a felület helyzetétől a körülvevő térben, és a görbületi számításokhoz szükséges. A
h
β
α
{\displaystyle h_{\ \beta }^{\alpha }}
h
β
α
=
∑
γ
=
1
2
g
~
α
γ
h
γ
β
=
1
g
~
(
G
L
−
F
M
G
M
−
F
N
−
F
L
+
E
M
−
F
M
+
E
N
)
β
α
{\displaystyle h_{\ \beta }^{\alpha }=\sum _{\gamma =1}^{2}{\tilde {g}}^{\alpha \gamma }h_{\gamma \beta }={\frac {1}{\tilde {g}}}\left({\begin{array}{cc}GL-FM&GM-FN\\-FL+EM&-FM+EN\end{array}}\right)_{\ \beta }^{\alpha }}
a főgörbületek (
h
β
α
{\displaystyle h_{\ \beta }^{\alpha }}
H
=
trace
(
h
β
α
)
/
2
{\displaystyle H=\operatorname {trace} \left(h_{\ \beta }^{\alpha }\right)/2}
K
=
det
(
h
β
α
)
{\displaystyle K=\det \left(h_{\ \beta }^{\alpha }\right)}
A Riemann-féle görbületi tenzor kifejezhető a
R
α
β
γ
ν
=
h
β
ν
h
α
γ
−
h
γ
ν
h
α
β
{\displaystyle R_{\ \alpha \beta \gamma }^{\nu }=h_{\ \beta }^{\nu }h_{\alpha \gamma }-h_{\ \gamma }^{\nu }h_{\alpha \beta }}
∇
γ
h
α
β
−
∇
β
h
α
γ
=
0
{\displaystyle \nabla _{\gamma }h_{\alpha \beta }-\nabla _{\beta }h_{\alpha \gamma }=0}
Mainardi-Codazzi-egyenletek .
Integrációs elemek három dimenzióban [ szerkesztés ] Egy vektoriális
d
r
→
{\displaystyle \mathrm {d} {\vec {r}}}
d
r
→
=
∑
i
=
1
3
∂
r
→
∂
u
i
d
u
i
=
∑
i
=
1
3
b
→
u
i
d
u
i
=
∑
i
=
1
3
e
→
u
i
h
u
i
d
u
i
{\displaystyle {\text{d}}{\vec {r}}=\sum \limits _{i=1}^{3}{{\frac {\partial {\vec {r}}}{\partial u_{i}}}{\text{d}}u_{i}}=\sum \limits _{i=1}^{3}{{\vec {b}}_{u_{i}}{\text{d}}u_{i}}=\sum \limits _{i=1}^{3}{{\vec {e}}_{u_{i}}h_{u_{i}}{\text{d}}u_{i}}}
Az
u
i
{\displaystyle u_{i}}
d
r
→
u
i
=
b
→
u
i
d
u
i
=
e
→
u
i
h
u
i
d
u
i
{\displaystyle \operatorname {d} {\vec {r}}_{u_{i}}={\vec {b}}_{u_{i}}\operatorname {d} u_{i}={\vec {e}}_{u_{i}}h_{u_{i}}\operatorname {d} u_{i}}
Ügyeljünk arra, hogy
d
r
→
u
i
{\displaystyle \operatorname {d} {\vec {r}}_{u_{i}}}
A skaláris útelem vagy hosszelem, illetve ívelem definíció szerint
d
s
=
|
d
r
→
|
{\displaystyle {\text{d}}s=|{\text{d}}{\vec {r}}\,|}
d
s
=
d
r
→
2
=
∑
i
=
1
3
d
r
→
u
i
⋅
d
r
→
u
i
=
∑
i
,
j
=
1
3
b
→
u
i
⋅
b
→
u
j
d
u
i
d
u
j
=
∑
i
,
j
=
1
3
g
i
j
d
u
i
d
u
j
=
g
11
(
d
u
1
)
2
+
g
22
(
d
u
2
)
2
+
g
33
(
d
u
3
)
2
+
2
g
12
d
u
1
d
u
2
+
2
g
13
d
u
1
d
u
3
+
2
g
23
d
u
2
d
u
3
{\displaystyle {\begin{aligned}{\text{d}}s&={\sqrt {{\text{d}}{\vec {r}}\,^{2}}}={\sqrt {\sum _{i=1}^{3}\operatorname {d} {\vec {r}}_{u_{i}}\cdot \operatorname {d} {\vec {r}}_{u_{i}}}}={\sqrt {\sum _{i,j=1}^{3}{\vec {b}}_{u_{i}}\cdot {\vec {b}}_{u_{j}}{\text{d}}u_{i}{\text{d}}u_{j}}}={\sqrt {\sum _{i,j=1}^{3}g_{ij}\,{\text{d}}u_{i}{\text{d}}u_{j}}}\\&={\sqrt {g_{11}\left({\text{d}}u_{1}\right)^{2}+g_{22}\left({\text{d}}u_{2}\right)^{2}+g_{33}\left({\text{d}}u_{3}\right)^{2}+2g_{12}{\text{d}}u_{1}{\text{d}}u_{2}+2g_{13}{\text{d}}u_{1}{\text{d}}u_{3}+2g_{23}{\text{d}}u_{2}{\text{d}}u_{3}}}\end{aligned}}}
Normált bázisvektorokkal:
d
s
=
(
h
u
1
d
u
1
)
2
+
⋯
+
2
(
e
→
u
1
⋅
e
→
u
2
)
h
u
1
h
u
2
d
u
1
d
u
2
+
⋯
{\displaystyle {\text{d}}s={\sqrt {\left(h_{u_{1}}{\text{d}}u_{1}\right)^{2}+\dots +2\left({\vec {e}}_{u_{1}}\cdot {\vec {e}}_{u_{2}}\right)h_{u_{1}}h_{u_{2}}{\text{d}}u_{1}{\text{d}}u_{2}+\cdots }}}
Az
e
→
u
i
⋅
e
→
u
j
=
δ
i
j
{\displaystyle {\vec {e}}_{u_{i}}\cdot {\vec {e}}_{u_{j}}=\delta _{ij}}
g
i
j
=
h
u
i
2
δ
i
j
{\displaystyle g_{ij}=h_{u_{i}}^{2}\delta _{ij}}
d
s
=
(
h
u
1
d
u
1
)
2
+
(
h
u
2
d
u
2
)
2
+
(
h
u
3
d
u
3
)
2
{\displaystyle {\text{d}}s={\sqrt {\left(h_{u_{1}}{\text{d}}u_{1}\right)^{2}+\left(h_{u_{2}}{\text{d}}u_{2}\right)^{2}+\left(h_{u_{3}}{\text{d}}u_{3}\right)^{2}}}}
Speciálisan, ha a görbe a
u
3
=
const
{\displaystyle u_{3}={\text{const}}}
d
s
=
(
h
u
1
d
u
1
)
2
+
(
h
u
2
d
u
2
)
2
+
2
(
e
→
u
1
⋅
e
→
u
2
)
h
u
1
h
u
2
d
u
1
d
u
2
=
E
(
d
u
1
)
2
+
G
(
d
u
2
)
2
+
2
F
d
u
1
d
u
2
{\displaystyle {\begin{aligned}{\text{d}}s&={\sqrt {\left(h_{u_{1}}{\text{d}}u_{1}\right)^{2}+\left(h_{u_{2}}{\text{d}}u_{2}\right)^{2}+2\left({\vec {e}}_{u_{1}}\cdot {\vec {e}}_{u_{2}}\right)h_{u_{1}}h_{u_{2}}{\text{d}}u_{1}{\text{d}}u_{2}}}\\&={\sqrt {E\left({\text{d}}u_{1}\right)^{2}+G\left({\text{d}}u_{2}\right)^{2}+2F{\text{d}}u_{1}{\text{d}}u_{2}}}\end{aligned}}}
Egy koordinátafelület felszíneleme:
d
A
→
=
∑
i
=
1
3
d
A
→
i
ahol
ϵ
i
j
k
d
A
→
i
=
±
d
r
→
u
j
×
d
r
→
u
k
=
±
b
→
u
j
×
b
→
u
k
d
u
j
d
u
k
=
±
g
b
→
u
i
∗
d
u
j
d
u
k
{\displaystyle {\text{d}}{\vec {A}}=\sum _{i=1}^{3}{\text{d}}{\vec {A}}_{i}\quad {\text{ahol}}\quad \epsilon _{ijk}{\text{d}}{\vec {A}}_{i}=\pm {\text{d}}{\vec {r}}_{u_{j}}\times {\text{d}}{\vec {r}}_{u_{k}}=\pm {\vec {b}}_{u_{j}}\times {\vec {b}}_{u_{k}}\,{\text{d}}u_{j}{\text{d}}u_{k}=\pm {\sqrt {g}}\,{\vec {b}}_{u_{i}}^{\ *}\,{\text{d}}u_{j}{\text{d}}u_{k}}
Az előjelet az irányítás adja meg. A
d
A
=
|
d
A
→
|
{\displaystyle {\text{d}}A=|{\text{d}}{\vec {A}}|}
Az általánosság megszorítása nélkül tekinthetjük az
u
3
=
const
{\displaystyle u_{3}={\text{const}}}
d
A
→
3
=
±
d
r
→
u
1
×
d
r
→
u
2
=
±
b
→
u
1
×
b
→
u
2
d
u
1
d
u
2
=
±
g
b
→
u
3
∗
d
u
1
d
u
2
{\displaystyle {\text{d}}{\vec {A}}_{3}=\pm {\text{d}}{\vec {r}}_{u_{1}}\times {\text{d}}{\vec {r}}_{u_{2}}=\pm {\vec {b}}_{u_{1}}\times {\vec {b}}_{u_{2}}\,{\text{d}}u_{1}{\text{d}}u_{2}=\pm {\sqrt {g}}\,{\vec {b}}_{u_{3}}^{\ *}\,{\text{d}}u_{1}{\text{d}}u_{2}}
d
A
3
=
|
d
A
→
3
|
=
|
b
→
u
1
×
b
→
u
2
|
d
u
1
d
u
2
=
|
g
b
→
u
3
∗
|
d
u
1
d
u
2
=
|
n
→
|
d
u
1
d
u
2
=
b
→
u
1
2
b
→
u
2
2
−
(
b
→
u
1
⋅
b
→
u
2
)
2
d
u
1
d
u
2
=
E
G
−
F
2
d
u
1
d
u
2
=
g
~
d
u
1
d
u
2
{\displaystyle {\begin{aligned}{\text{d}}A_{3}&=\left|{\text{d}}{\vec {A}}_{3}\right|=\left|{\vec {b}}_{u_{1}}\times {\vec {b}}_{u_{2}}\right|{\text{d}}u_{1}{\text{d}}u_{2}=\left|{\sqrt {g}}\,{\vec {b}}_{u_{3}}^{\ *}\right|{\text{d}}u_{1}{\text{d}}u_{2}=\left|{\vec {n}}\right|{\text{d}}u_{1}{\text{d}}u_{2}\\&={\sqrt {{\vec {b}}_{u_{1}}^{\ 2}{\vec {b}}_{u_{2}}^{\ 2}-\left({\vec {b}}_{u_{1}}\cdot {\vec {b}}_{u_{2}}\right)^{2}}}{\text{d}}u_{1}{\text{d}}u_{2}={\sqrt {EG-F^{2}}}\,{\text{d}}u_{1}{\text{d}}u_{2}={\sqrt {\tilde {g}}}\,{\text{d}}u_{1}{\text{d}}u_{2}\end{aligned}}}
Normált bázisvektorokkal:
d
A
→
3
=
±
e
→
u
1
×
e
→
u
2
h
u
1
h
u
2
d
u
1
d
u
2
{\displaystyle {\text{d}}{\vec {A}}_{3}=\pm {\vec {e}}_{u_{1}}\times {\vec {e}}_{u_{2}}h_{u_{1}}h_{u_{2}}{\text{d}}u_{1}{\text{d}}u_{2}}
d
A
3
=
|
e
→
u
1
×
e
→
u
2
|
|
h
u
1
h
u
2
|
d
u
1
d
u
2
{\displaystyle {\text{d}}A_{3}=\left|{\vec {e}}_{u_{1}}\times {\vec {e}}_{u_{2}}\right|\left|h_{u_{1}}h_{u_{2}}\right|{\text{d}}u_{1}{\text{d}}u_{2}}
Ortogonális koordináták esetén:
d
A
→
3
=
±
e
→
u
3
h
u
1
h
u
2
d
u
1
d
u
2
=
±
e
→
u
3
E
G
d
u
1
d
u
2
{\displaystyle {\text{d}}{\vec {A}}_{3}=\pm {\vec {e}}_{u_{3}}h_{u_{1}}h_{u_{2}}{\text{d}}u_{1}{\text{d}}u_{2}=\pm {\vec {e}}_{u_{3}}{\sqrt {EG}}\,{\text{d}}u_{1}{\text{d}}u_{2}}
d
A
3
=
|
h
u
1
h
u
2
|
d
u
1
d
u
2
=
E
G
d
u
1
d
u
2
{\displaystyle {\text{d}}A_{3}=\left|h_{u_{1}}h_{u_{2}}\right|{\text{d}}u_{1}{\text{d}}u_{2}={\sqrt {EG}}\,{\text{d}}u_{1}{\text{d}}u_{2}}
A térfogatelem:
d
V
=
|
d
r
→
u
1
⋅
(
d
r
→
u
2
×
d
r
→
u
3
)
|
=
|
det
[
d
r
→
u
1
,
d
r
→
u
1
,
d
r
→
u
3
]
|
=
|
det
[
b
→
u
1
,
b
→
u
2
,
b
→
u
3
]
|
d
u
1
d
u
2
d
u
3
=
|
g
|
d
u
1
d
u
2
d
u
3
{\displaystyle {\text{d}}V=\left|{\text{d}}{\vec {r}}_{u_{1}}\cdot \left({\text{d}}{\vec {r}}_{u_{2}}\times {\text{d}}{\vec {r}}_{u_{3}}\right)\right|=\left|\det[{\text{d}}{\vec {r}}_{u_{1}},{\text{d}}{\vec {r}}_{u_{1}},{\text{d}}{\vec {r}}_{u_{3}}]\right|=\left|\det[{\vec {b}}_{u_{1}},{\vec {b}}_{u_{2}},{\vec {b}}_{u_{3}}]\right|{\text{d}}u_{1}{\text{d}}u_{2}{\text{d}}u_{3}=\left|{\sqrt {g}}\right|{\text{d}}u_{1}{\text{d}}u_{2}{\text{d}}u_{3}}
ahol azonosítható a
g
{\displaystyle {\sqrt {g}}}
Normált bázisvektorokra:
d
V
=
|
det
[
e
→
u
1
,
e
→
u
2
,
e
→
u
3
]
|
|
h
u
1
h
u
2
h
u
3
|
d
u
1
d
u
2
d
u
3
=
|
g
|
d
u
1
d
u
2
d
u
3
{\displaystyle {\text{d}}V=\left|\det[{\vec {e}}_{u_{1}},{\vec {e}}_{u_{2}},{\vec {e}}_{u_{3}}]\right|\left|h_{u_{1}}h_{u_{2}}h_{u_{3}}\right|{\text{d}}u_{1}{\text{d}}u_{2}{\text{d}}u_{3}=\left|{\sqrt {g}}\right|{\text{d}}u_{1}{\text{d}}u_{2}{\text{d}}u_{3}}
Ortogonáls koordinátákban:
d
V
=
|
h
u
1
h
u
2
h
u
3
|
d
u
1
d
u
2
d
u
3
{\displaystyle {\text{d}}V=\left|h_{u_{1}}h_{u_{2}}h_{u_{3}}\right|{\text{d}}u_{1}{\text{d}}u_{2}{\text{d}}u_{3}}
Differenciáloperátorok három dimenzióban [ szerkesztés ] Az ortogonális koordináta-rendszerek speciális esete több különböző szempontból is fontos, például mérnökök és fizikusok számára. Többek között azért, mert a leggyakrabban használt görbe vonalú koordináta-rendszerek, például a gömbi és az elliptikus, ortogonálisak. Más szempontból azért is fontosak, mert itt nem kell foglalkozni a kovariáns, a kontravariáns, a duális, a gamma-együttható és további kapcsolódó fogalmakkal. Továbbá a bázisok mindig ortogonálisak, habár nem mindig normáltak. Ortonormált rendszert a normált bázisok alkotnak. A normált vektorokat
^
{\displaystyle {\hat {}}}
Ortogonális koordináta-rendszerekben a következő differenciáloperátorokat adják meg: gradiens , divergencia , rotáció , Laplace-operátor . Egy
ϕ
(
r
)
{\displaystyle \phi (\mathbf {r} )}
d
i
v
a
(
r
)
{\displaystyle {\rm {{div}\ \mathbf {a} (\mathbf {r} )}}}
skalármező , illetve
r
o
t
a
{\displaystyle {\rm {{rot}\ \mathbf {a} }}}
vektormező a forrás- és örvénysűrűséget jelenti. Jelentésük független a koordinátáktól.
A
Φ
(
u
)
{\displaystyle \Phi (\mathbf {u} )}
∇
→
Φ
=
∑
i
=
1
3
e
→
u
i
1
h
u
i
∂
Φ
∂
u
i
=
e
→
u
1
1
h
u
1
∂
Φ
∂
u
1
+
e
→
u
2
1
h
u
2
∂
Φ
∂
u
2
+
e
→
u
3
1
h
u
3
∂
Φ
∂
u
3
{\displaystyle {\begin{aligned}{\vec {\nabla }}\Phi &=\sum \limits _{i=1}^{3}{{\vec {e}}_{u_{i}}{\frac {1}{h_{u_{i}}}}{\frac {\partial \Phi }{\partial u_{i}}}}\\&={\vec {e}}_{u_{1}}{\frac {1}{h_{u_{1}}}}{\frac {\partial \Phi }{\partial u_{1}}}+{\vec {e}}_{u_{2}}{\frac {1}{h_{u_{2}}}}{\frac {\partial \Phi }{\partial u_{2}}}+{\vec {e}}_{u_{3}}{\frac {1}{h_{u_{3}}}}{\frac {\partial \Phi }{\partial u_{3}}}\end{aligned}}}
Vegyük észre, hogy nemcsak
Φ
{\displaystyle \Phi }
h
{\displaystyle h}
u -tól.
Egy vektormező divergenciája:
∇
→
⋅
a
→
=
1
h
u
1
h
u
2
h
u
3
∑
j
=
1
3
∂
∂
u
j
(
h
u
1
h
u
2
h
u
3
h
u
j
a
u
j
)
=
1
h
u
1
h
u
2
h
u
3
[
∂
∂
u
1
(
h
u
2
h
u
3
a
u
1
)
+
∂
∂
u
2
(
h
u
1
h
u
3
a
u
2
)
+
∂
∂
u
3
(
h
u
1
h
u
2
a
u
3
)
]
{\displaystyle {\begin{aligned}{\vec {\nabla }}\cdot {\vec {a}}&={\frac {1}{h_{u_{1}}h_{u_{2}}h_{u_{3}}}}\sum _{j=1}^{3}{\frac {\partial }{\partial u_{j}}}\left({\frac {h_{u_{1}}h_{u_{2}}h_{u_{3}}}{h_{u_{j}}}}a_{u_{j}}\right)\\&={\frac {1}{h_{u_{1}}h_{u_{2}}h_{u_{3}}}}\left[{\frac {\partial }{\partial u_{1}}}\left(h_{u_{2}}h_{u_{3}}a_{u_{1}}\right)+{\frac {\partial }{\partial u_{2}}}\left(h_{u_{1}}h_{u_{3}}a_{u_{2}}\right)+{\frac {\partial }{\partial u_{3}}}\left(h_{u_{1}}h_{u_{2}}a_{u_{3}}\right)\right]\end{aligned}}}
Egy vektormező rotációja:
∇
→
×
a
→
=
1
h
u
1
h
u
2
h
u
3
∑
i
,
j
,
k
=
1
3
ϵ
i
j
k
h
u
i
e
→
u
i
∂
∂
u
j
(
h
u
k
a
u
k
)
=
1
h
u
1
h
u
2
h
u
3
|
h
u
1
e
→
u
1
h
u
2
e
→
u
2
h
u
3
e
→
u
3
∂
∂
u
1
∂
∂
u
2
∂
∂
u
3
h
u
1
a
u
1
h
u
2
a
u
2
h
u
3
a
u
3
|
=
e
→
u
1
h
u
2
h
u
3
(
∂
(
h
u
3
a
u
3
)
∂
u
2
−
∂
(
h
u
2
a
u
2
)
∂
u
3
)
+
e
→
u
2
h
u
1
h
u
3
(
∂
(
h
u
1
a
u
1
)
∂
u
3
−
∂
(
h
u
3
a
u
3
)
∂
u
1
)
+
e
→
u
3
h
u
1
h
u
2
(
∂
(
h
u
2
a
u
2
)
∂
u
1
−
∂
(
h
u
1
a
u
1
)
∂
u
2
)
{\displaystyle {\begin{aligned}{\vec {\nabla }}\times {\vec {a}}&={\frac {1}{h_{u_{1}}h_{u_{2}}h_{u_{3}}}}\sum _{i,j,k=1}^{3}\epsilon _{ijk}h_{u_{i}}{\vec {e}}_{u_{i}}{\frac {\partial }{\partial u_{j}}}\left(h_{u_{k}}a_{u_{k}}\right)\\&={\frac {1}{h_{u_{1}}h_{u_{2}}h_{u_{3}}}}\left|{\begin{matrix}h_{u_{1}}{\vec {e}}_{u_{1}}&h_{u_{2}}{\vec {e}}_{u_{2}}&h_{u_{3}}{\vec {e}}_{u_{3}}\\{\frac {\partial }{\partial u_{1}}}&{\frac {\partial }{\partial u_{2}}}&{\frac {\partial }{\partial u_{3}}}\\h_{u_{1}}a_{u_{1}}&h_{u_{2}}a_{u_{2}}&h_{u_{3}}a_{u_{3}}\end{matrix}}\right|\\&={\frac {{\vec {e}}_{u_{1}}}{h_{u_{2}}h_{u_{3}}}}\left({\frac {\partial (h_{u_{3}}a_{u_{3}})}{\partial u_{2}}}-{\frac {\partial (h_{u_{2}}a_{u_{2}})}{\partial u_{3}}}\right)+{\frac {{\vec {e}}_{u_{2}}}{h_{u_{1}}h_{u_{3}}}}\left({\frac {\partial (h_{u_{1}}a_{u_{1}})}{\partial u_{3}}}-{\frac {\partial (h_{u_{3}}a_{u_{3}})}{\partial u_{1}}}\right)+{\frac {{\vec {e}}_{u_{3}}}{h_{u_{1}}h_{u_{2}}}}\left({\frac {\partial (h_{u_{2}}a_{u_{2}})}{\partial u_{1}}}-{\frac {\partial (h_{u_{1}}a_{u_{1}})}{\partial u_{2}}}\right)\end{aligned}}}
A Laplace-operátor:
Δ
Φ
=
1
h
u
1
h
u
2
h
u
3
∑
j
=
1
3
∂
∂
u
j
(
h
u
1
h
u
2
h
u
3
h
u
j
2
∂
Φ
∂
u
j
)
=
1
h
u
1
h
u
2
h
u
3
[
∂
∂
u
1
(
h
u
2
h
u
3
h
u
1
∂
Φ
∂
u
1
)
+
∂
∂
u
2
(
h
u
1
h
u
3
h
u
2
∂
Φ
∂
u
2
)
+
∂
∂
u
3
(
h
u
1
h
u
2
h
u
3
∂
Φ
∂
u
3
)
]
{\displaystyle {\begin{aligned}\Delta \Phi &={\frac {1}{h_{u_{1}}h_{u_{2}}h_{u_{3}}}}\sum _{j=1}^{3}{\frac {\partial }{\partial u_{j}}}\left({\frac {h_{u_{1}}h_{u_{2}}h_{u_{3}}}{h_{u_{j}}^{2}}}{\frac {\partial \Phi }{\partial u_{j}}}\right)\\&={\frac {1}{h_{u_{1}}h_{u_{2}}h_{u_{3}}}}\left[{\frac {\partial }{\partial u_{1}}}\left({\frac {h_{u_{2}}h_{u_{3}}}{h_{u_{1}}}}{\frac {\partial \Phi }{\partial u_{1}}}\right)+{\frac {\partial }{\partial u_{2}}}\left({\frac {h_{u_{1}}h_{u_{3}}}{h_{u_{2}}}}{\frac {\partial \Phi }{\partial u_{2}}}\right)+{\frac {\partial }{\partial u_{3}}}\left({\frac {h_{u_{1}}h_{u_{2}}}{h_{u_{3}}}}{\frac {\partial \Phi }{\partial u_{3}}}\right)\right]\end{aligned}}}
Tehát nem elég a
Δ
=
∇
2
{\displaystyle \Delta =\nabla ^{2}}
Δ
Φ
=
d
i
v
g
r
a
d
ϕ
{\displaystyle \Delta \Phi ={\rm {{div\ grad}\ \phi }}}
Két dimenzióban több hasznos koordináta-rendszert konform leképezéssel hoztak létre. Ezek nemcsak hogy derékszögűek, hanem szögtartóak tetszőleges szögre. Ez azt is jelenti, hogy két bázisvektor hosszának aránya mindig egy, például
|
h
u
k
|
:
|
h
u
1
|
,
k
=
2
,
3
,
…
,
{\displaystyle |h_{u_{k}}|:|h_{u_{1}}|,\ k=2,3,\dots ,}
k -tól függetlenül, különben a gömbből ellipszoid lenne.
Differenciáloperátorok általános koordináta-rendszerben [ szerkesztés ] A következőkben a természetes bázist, és a tenzoranalízisben megszokott jelöléseket használjuk. Azaz a felső index kontravarianciát, az alsó index kovarianciát jelez. Legyen továbbá
Φ
{\displaystyle \Phi }
a
→
=
a
i
b
→
i
=
a
i
b
→
i
{\displaystyle {\vec {a}}=a^{i}{\vec {b}}_{i}=a_{i}{\vec {b}}^{\,\,i}}
Továbbá az írásmód
∂
i
=
∂
∂
x
i
{\displaystyle \partial _{i}={\tfrac {\partial }{\partial x^{i}}}}
Γ
i
k
j
{\displaystyle \Gamma _{ik}^{j}}
∂
k
b
→
i
=
∑
j
Γ
i
k
j
b
→
j
{\displaystyle \partial _{k}{\vec {b}}_{i}=\sum _{j}\Gamma _{ik}^{j}{\vec {b}}_{j}}
∇
i
{\displaystyle \nabla _{i}}
∇
k
Φ
=
∂
k
Φ
{\displaystyle \nabla _{k}\Phi =\partial _{k}\Phi }
∇
k
a
i
=
∂
k
a
i
+
∑
j
Γ
k
j
i
a
j
{\displaystyle \nabla _{k}a^{i}=\partial _{k}a^{i}+\sum _{j}\Gamma _{kj}^{i}a^{j}}
∇
k
a
i
=
∂
k
a
i
−
∑
j
Γ
k
i
j
a
j
{\displaystyle \nabla _{k}a_{i}=\partial _{k}a_{i}-\sum _{j}\Gamma _{ki}^{j}a_{j}}
Skalármező gradiense:
g
r
a
d
Φ
=
∑
i
(
∇
i
Φ
)
b
→
i
=
∑
i
(
∂
i
Φ
)
b
→
i
{\displaystyle \mathrm {grad} \,\Phi =\sum _{i}(\nabla _{i}\Phi ){\vec {b}}^{\,\,i}=\sum _{i}(\partial _{i}\Phi ){\vec {b}}^{\,\,i}}
Tenzormező gradiense:
Egy
n
≥
1
{\displaystyle n\geq 1}
A
{\displaystyle A}
g
r
a
d
A
=
A
⊗
∇
=
∑
k
(
∂
k
A
)
⊗
b
→
k
{\displaystyle \mathrm {grad} \,A=A\otimes \nabla =\sum _{k}(\partial _{k}A)\otimes {\vec {b}}^{\,\,k}}
g
r
a
d
A
=
∇
⊗
A
=
∑
k
b
→
k
⊗
(
∂
k
A
)
{\displaystyle \mathrm {grad} \,A=\nabla \otimes A=\sum _{k}{\vec {b}}^{\,\,k}\otimes (\partial _{k}A)}
A továbbiakban a jobbgradienst használjuk.
Vektormező gradiense:
g
r
a
d
a
→
=
∑
k
(
∂
k
a
→
)
⊗
b
→
k
=
∑
i
,
k
(
∇
k
a
i
)
b
→
i
⊗
b
→
k
=
∑
i
,
k
(
∂
k
a
i
+
a
l
Γ
l
k
i
)
b
→
i
⊗
b
→
k
=
∑
i
,
k
(
∇
k
a
i
)
b
→
i
⊗
b
→
k
=
∑
i
,
k
(
∂
k
a
i
−
a
l
Γ
i
k
l
)
b
→
i
⊗
b
→
k
{\displaystyle {\begin{aligned}\mathrm {grad} \,{\vec {a}}&=\sum _{k}(\partial _{k}{\vec {a}})\otimes {\vec {b}}^{\,\,k}\\&=\sum _{i,k}(\nabla _{k}a^{i}){\vec {b}}_{i}\otimes {\vec {b}}^{\,\,k}=\sum _{i,k}(\partial _{k}a^{i}+a^{l}\Gamma _{lk}^{i}){\vec {b}}_{i}\otimes {\vec {b}}^{\,\,k}\\&=\sum _{i,k}(\nabla _{k}a_{i}){\vec {b}}^{\,\,i}\otimes {\vec {b}}^{\,\,k}=\sum _{i,k}(\partial _{k}a_{i}-a_{l}\Gamma _{ik}^{l}){\vec {b}}^{\,\,i}\otimes {\vec {b}}^{\,\,k}\end{aligned}}}
Másodfokú tenzor gradiense:
g
r
a
d
a
→
=
∑
k
(
∂
k
a
→
)
⊗
b
→
k
=
∑
i
,
k
(
∇
k
a
i
)
b
→
i
⊗
b
→
k
=
∑
i
,
k
(
∂
k
a
i
+
a
l
Γ
l
k
i
)
b
→
i
⊗
b
→
k
=
∑
i
,
k
(
∇
k
a
i
)
b
→
i
⊗
b
→
k
=
∑
i
,
k
(
∂
k
a
i
−
a
l
Γ
i
k
l
)
b
→
i
⊗
b
→
k
{\displaystyle {\begin{aligned}\mathrm {grad} \,{\vec {a}}&=\sum _{k}(\partial _{k}{\vec {a}})\otimes {\vec {b}}^{\,\,k}\\&=\sum _{i,k}(\nabla _{k}a^{i}){\vec {b}}_{i}\otimes {\vec {b}}^{\,\,k}=\sum _{i,k}(\partial _{k}a^{i}+a^{l}\Gamma _{lk}^{i}){\vec {b}}_{i}\otimes {\vec {b}}^{\,\,k}\\&=\sum _{i,k}(\nabla _{k}a_{i}){\vec {b}}^{\,\,i}\otimes {\vec {b}}^{\,\,k}=\sum _{i,k}(\partial _{k}a_{i}-a_{l}\Gamma _{ik}^{l}){\vec {b}}^{\,\,i}\otimes {\vec {b}}^{\,\,k}\end{aligned}}}
Vektormező divergenciája:
d
i
v
a
→
=
Tr
(
g
r
a
d
a
→
)
=
∑
i
∇
i
a
i
=
∑
i
∂
i
a
i
+
∑
i
,
j
Γ
i
j
i
a
j
=
∑
i
,
k
∇
i
a
k
g
i
k
=
∑
k
(
∑
i
∂
i
a
k
−
∑
i
,
j
Γ
i
k
j
a
j
)
g
i
k
=
∑
i
1
g
∂
i
(
g
a
i
)
{\displaystyle {\begin{aligned}\mathrm {div} \,{\vec {a}}&=\operatorname {Tr} (\mathrm {grad} \,{\vec {a}})\\&=\sum _{i}\nabla _{i}a^{i}=\sum _{i}\partial _{i}a^{i}+\sum _{i,j}\Gamma _{ij}^{i}a^{j}\\&=\sum _{i,k}\nabla _{i}a_{k}g^{ik}=\sum _{k}\left(\sum _{i}\partial _{i}a_{k}-\sum _{i,j}\Gamma _{ik}^{j}a_{j}\right)g^{ik}\\&=\sum _{i}{\frac {1}{\sqrt {g}}}\partial _{i}({\sqrt {g}}a^{i})\end{aligned}}}
Tenzormező divergenciája:
Az
n
≥
2
{\displaystyle n\geq 2}
A
{\displaystyle A}
d
i
v
A
=
A
⋅
∇
{\displaystyle \mathrm {div} \,A=A\cdot \nabla }
d
i
v
A
=
∇
⋅
A
{\displaystyle \mathrm {div} \,A=\nabla \cdot A}
Másodfokú tenzor divergenciája:
div
S
_
_
=
∑
i
,
j
,
k
∂
k
[
S
i
j
b
→
i
⊗
b
→
j
]
⋅
b
→
k
=
∑
i
,
j
,
k
[
∇
k
S
i
j
]
b
→
i
⊗
b
→
j
⋅
b
→
k
⏟
δ
j
k
=
∑
i
,
k
[
∇
k
S
i
k
]
b
→
i
=
∑
i
,
j
,
k
∂
k
[
S
i
j
b
→
i
⊗
b
→
j
]
⋅
b
→
k
=
∑
i
,
j
,
k
[
∇
k
S
i
j
]
b
→
i
⊗
b
→
j
⋅
b
→
k
⏟
δ
j
k
=
∑
i
,
k
[
∇
k
S
i
k
]
b
→
i
=
∑
i
,
j
,
k
∂
k
[
S
j
i
b
→
i
⊗
b
→
j
]
⋅
b
→
k
=
∑
i
,
j
,
k
[
∇
k
S
j
i
]
b
→
i
⊗
b
→
j
⋅
b
→
k
⏟
g
j
k
=
∑
i
,
k
[
∇
k
S
i
k
]
b
→
i
=
∑
i
,
j
,
k
∂
k
[
S
i
j
b
→
i
⊗
b
→
j
]
⋅
b
→
k
=
∑
i
,
j
,
k
[
∇
k
S
i
j
]
b
→
i
⊗
b
→
j
⋅
b
→
k
⏟
g
j
k
=
∑
i
,
k
[
∇
k
S
i
k
]
b
→
i
{\displaystyle {\begin{aligned}\operatorname {div} {\underline {\underline {S}}}&=\sum _{i,j,k}\partial _{k}[S^{ij}\,{\vec {b}}_{i}\otimes {\vec {b}}_{j}]\cdot {\vec {b}}^{~k}=\sum _{i,j,k}\left[\nabla _{k}S^{ij}\right]{\vec {b}}_{i}\otimes \underbrace {{\vec {b}}_{j}\cdot {\vec {b}}^{~k}} _{\delta _{j}^{k}}=\sum _{i,k}\left[\nabla _{k}S^{ik}\right]{\vec {b}}_{i}\\&=\sum _{i,j,k}\partial _{k}[S_{i}^{~j}\,{\vec {b}}^{~i}\otimes {\vec {b}}_{j}]\cdot {\vec {b}}^{~k}=\sum _{i,j,k}\left[\nabla _{k}S_{i}^{~j}\right]{\vec {b}}^{~i}\otimes \underbrace {{\vec {b}}_{j}\cdot {\vec {b}}^{~k}} _{\delta _{j}^{k}}=\sum _{i,k}\left[\nabla _{k}S_{i}^{~k}\right]{\vec {b}}^{~i}\\&=\sum _{i,j,k}\partial _{k}[S_{~j}^{i}\,{\vec {b}}_{i}\otimes {\vec {b}}^{~j}]\cdot {\vec {b}}^{~k}=\sum _{i,j,k}\left[\nabla _{k}S_{~j}^{i}\right]{\vec {b}}_{i}\otimes \underbrace {{\vec {b}}^{~j}\cdot {\vec {b}}^{~k}} _{g^{jk}}=\sum _{i,k}\left[\nabla _{k}S^{ik}\right]{\vec {b}}_{i}\\&=\sum _{i,j,k}\partial _{k}[S_{ij}\,{\vec {b}}^{~i}\otimes {\vec {b}}^{~j}]\cdot {\vec {b}}^{~k}=\sum _{i,j,k}\left[\nabla _{k}S_{ij}\right]{\vec {b}}^{~i}\otimes \underbrace {{\vec {b}}^{~j}\cdot {\vec {b}}^{~k}} _{g^{jk}}=\sum _{i,k}\left[\nabla _{k}S_{i}^{~k}\right]{\vec {b}}^{~i}\end{aligned}}}
Tenzormező rotációja:
Egy
n
≥
1
{\displaystyle n\geq 1}
A
{\displaystyle A}
r
o
t
A
=
A
⊗
∇
{\displaystyle \mathrm {rot} \,A=A\otimes \nabla }
r
o
t
A
=
∇
⊗
A
{\displaystyle \mathrm {rot} \,A=\nabla \otimes A}
A továbbiakban a jobbrotációt használjuk:
r
o
t
A
=
A
⊗
∇
=
−
A
×
∇
=
−
∂
k
A
×
b
→
k
{\displaystyle \mathrm {rot} \,A=A\otimes \nabla =-A\times \nabla =-\partial _{k}A\times {\vec {b}}^{\ k}}
Vektormező rotációja:
r
o
t
a
→
=
∑
i
,
j
,
k
E
i
j
k
∇
i
a
j
b
→
k
=
1
g
∑
i
,
j
,
k
ϵ
i
j
k
(
∂
i
a
j
)
b
→
k
=
1
g
|
b
→
1
b
→
2
b
→
3
∂
1
∂
2
∂
3
a
1
a
2
a
3
|
=
1
g
∑
i
,
j
,
k
,
l
ϵ
i
j
k
(
∂
i
a
l
g
j
l
)
b
→
k
=
∑
i
,
j
,
k
E
i
j
k
∇
i
a
j
b
→
k
=
g
∑
i
,
j
,
k
ϵ
i
j
k
(
∂
i
a
j
)
b
→
k
=
g
|
b
→
1
b
→
2
b
→
3
∂
1
∂
2
∂
3
a
1
a
2
a
3
|
{\displaystyle {\begin{aligned}\mathrm {rot} \,{\vec {a}}&=\sum _{i,j,k}{\mathcal {E}}^{ijk}\nabla _{i}a_{j}{\vec {b}}_{k}={\frac {1}{\sqrt {g}}}\sum _{i,j,k}\epsilon ^{ijk}(\partial _{i}a_{j}){\vec {b}}_{k}={\frac {1}{\sqrt {g}}}\left|{\begin{matrix}{\vec {b}}_{1}&{\vec {b}}_{2}&{\vec {b}}_{3}\\\partial _{1}&\partial _{2}&\partial _{3}\\a_{1}&a_{2}&a_{3}\end{matrix}}\right|={\frac {1}{\sqrt {g}}}\sum _{i,j,k,l}\epsilon ^{ijk}(\partial _{i}a^{l}g_{jl}){\vec {b}}_{k}\\&=\sum _{i,j,k}{\mathcal {E}}_{ijk}\nabla ^{i}a^{j}{\vec {b}}^{\ k}={\sqrt {g}}\sum _{i,j,k}\epsilon _{ijk}(\partial ^{i}a^{j}){\vec {b}}^{\ k}={\sqrt {g}}\left|{\begin{matrix}{\vec {b}}^{\ 1}&{\vec {b}}^{\ 2}&{\vec {b}}^{\ 3}\\\partial ^{1}&\partial ^{2}&\partial ^{3}\\a^{1}&a^{2}&a^{3}\end{matrix}}\right|\end{aligned}}}
Skalármező Laplace-operátora:
Δ
Φ
=
d
i
v
(
g
r
a
d
Φ
)
=
∑
i
∇
i
(
∇
i
Φ
)
=
∑
i
,
j
∇
i
g
i
j
∇
j
Φ
=
∑
i
,
j
∂
i
g
i
j
∂
j
Φ
+
∑
i
,
j
,
k
Γ
i
j
i
g
j
k
∂
k
Φ
=
∑
i
,
j
1
g
∂
i
(
g
g
i
j
∂
j
Φ
)
{\displaystyle {\begin{aligned}\Delta \Phi &=\mathrm {div} (\mathrm {grad} \,\Phi )\\&=\sum _{i}\nabla _{i}(\nabla ^{i}\Phi )=\sum _{i,j}\nabla _{i}g^{ij}\nabla _{j}\Phi =\sum _{i,j}\partial _{i}g^{ij}\partial _{j}\Phi +\sum _{i,j,k}\Gamma _{ij}^{i}g^{jk}\partial _{k}\Phi \\&=\sum _{i,j}{\frac {1}{\sqrt {g}}}\partial _{i}({\sqrt {g}}\,g^{ij}\partial _{j}\Phi )\end{aligned}}}
Gradiens és totális differenciál [ szerkesztés ] A következőkben a gradiens görbe vonalú koordináta-rendszerben vezetjük be. A helyvektor totális differenciálja előáll, mint:
d
r
→
=
∑
j
∂
j
r
→
d
u
j
=
∑
j
b
→
j
d
u
j
⇒
b
→
i
⋅
d
r
→
=
∑
j
b
→
i
⋅
b
→
j
⏟
δ
j
i
d
u
j
=
d
u
i
{\displaystyle \mathrm {d} {\vec {r}}=\sum _{j}\partial _{j}{\vec {r}}\,\mathrm {d} u^{j}=\sum _{j}{\vec {b}}_{j}\,\mathrm {d} u^{j}\quad \Rightarrow \quad {\vec {b}}^{\,\,i}\cdot \mathrm {d} {\vec {r}}=\sum _{j}\underbrace {{\vec {b}}^{\,\,i}\cdot {\vec {b}}_{j}} _{\delta _{j}^{i}}\,\mathrm {d} u^{j}=\mathrm {d} u^{i}}
Legyen most
Φ
{\displaystyle \Phi }
d
u
i
{\displaystyle \mathrm {d} u^{i}}
d
Φ
=
∑
i
(
∂
i
Φ
)
d
u
i
=
∑
i
(
∂
i
Φ
)
b
→
i
⋅
d
r
→
{\displaystyle \mathrm {d} \Phi =\sum _{i}(\partial _{i}\Phi )\,\mathrm {d} u^{i}=\sum _{i}(\partial _{i}\Phi )\,{\vec {b}}^{\,\,i}\cdot \mathrm {d} {\vec {r}}}
A
∇
Φ
{\displaystyle \nabla \Phi }
d
Φ
=
⟨
∇
Φ
,
d
r
→
⟩
=
∇
Φ
⋅
d
r
→
{\displaystyle \mathrm {d} \Phi =\langle \nabla \Phi ,\mathrm {d} {\vec {r}}\rangle =\nabla \Phi \cdot \mathrm {d} {\vec {r}}}
és azonosítható, mint:
∇
Φ
=
∑
i
(
∂
i
Φ
)
b
→
i
=
∑
i
∂
Φ
∂
u
i
b
→
i
{\displaystyle \nabla \Phi =\sum _{i}(\partial _{i}\Phi )\,{\vec {b}}^{\,\,i}=\sum _{i}{\frac {\partial \Phi }{\partial u^{i}}}\,{\vec {b}}^{\,\,i}}
Ortogonális koordinátákban egy kovariáns bázisvektor
b
→
i
=
h
i
e
→
i
{\displaystyle {\vec {b}}_{i}=h_{i}{\vec {e}}_{i}}
b
→
i
=
1
h
i
e
→
i
{\displaystyle {\vec {b}}^{\,\,i}={\frac {1}{h_{i}}}{\vec {e}}_{i}}
∇
Φ
=
∑
i
∂
Φ
∂
u
i
b
→
i
=
∑
i
∂
Φ
∂
u
i
1
h
i
e
→
i
{\displaystyle \nabla \Phi =\sum _{i}{\frac {\partial \Phi }{\partial u^{i}}}\,{\vec {b}}^{\,\,i}=\sum _{i}{\frac {\partial \Phi }{\partial u^{i}}}\,{\frac {1}{h_{i}}}{\vec {e}}_{i}}
Φ
=
u
k
{\displaystyle \Phi =u^{k}}
b
→
k
{\displaystyle {\vec {b}}^{\,\,k}}
u
k
=
const.
{\displaystyle u^{k}={\text{const.}}}
∇
u
k
=
∑
i
(
∂
i
u
k
)
b
→
i
=
∑
i
∂
u
k
∂
u
i
⏟
δ
i
k
b
→
i
=
b
→
k
{\displaystyle \nabla u^{k}=\sum _{i}(\partial _{i}u^{k})\,{\vec {b}}^{\,\,i}=\sum _{i}\underbrace {\frac {\partial u^{k}}{\partial u^{i}}} _{\delta _{i}^{k}}\,{\vec {b}}^{\,\,i}={\vec {b}}^{\,\,k}}
Speciális Christoffel-szimbólumok [ szerkesztés ] A divergencia kiszámításához szükség van a
Γ
i
j
i
{\displaystyle \Gamma _{ij}^{i}}
g
{\displaystyle g}
∑
i
Γ
i
j
i
=
∑
i
,
k
g
k
i
2
∂
g
i
k
∂
u
j
=
∑
i
,
k
1
2
g
∂
g
∂
g
i
k
∂
g
i
k
∂
u
j
=
1
2
g
∂
g
∂
u
j
=
1
2
g
∂
j
g
=
1
g
∂
j
g
{\displaystyle \sum _{i}\Gamma _{ij}^{i}=\sum _{i,k}{\cfrac {g^{ki}}{2}}{\frac {\partial g_{ik}}{\partial u^{j}}}=\sum _{i,k}{\cfrac {1}{2g}}{\frac {\partial g}{\partial g_{ik}}}{\frac {\partial g_{ik}}{\partial u^{j}}}={\cfrac {1}{2g}}{\frac {\partial g}{\partial u^{j}}}={\frac {1}{2g}}\partial _{j}g={\frac {1}{\sqrt {g}}}\partial _{j}{\sqrt {g}}}
ami következik abból, hogy
g
i
j
=
1
g
∂
g
∂
g
j
i
{\displaystyle g^{ij}={\frac {1}{g}}{\frac {\partial g}{\partial g_{ji}}}}
∑
i
j
g
i
j
∂
g
i
j
∂
u
k
=
∑
i
j
l
Γ
i
k
l
g
l
j
g
i
j
+
∑
i
j
l
Γ
j
k
l
g
i
l
g
i
j
=
∑
i
l
Γ
i
k
l
δ
l
i
+
∑
j
l
Γ
j
k
l
δ
l
j
=
∑
i
Γ
i
k
i
+
∑
j
Γ
j
k
j
=
2
∑
i
Γ
i
k
i
{\displaystyle \sum _{ij}g^{ij}{\frac {\partial g_{ij}}{\partial u_{k}}}=\sum _{ijl}\Gamma _{ik}^{l}g_{lj}g^{ij}+\sum _{ijl}\Gamma _{jk}^{l}g_{il}g^{ij}=\sum _{il}\Gamma _{ik}^{l}\delta _{l}^{i}+\sum _{jl}\Gamma _{jk}^{l}\delta _{l}^{j}=\sum _{i}\Gamma _{ik}^{i}+\sum _{j}\Gamma _{jk}^{j}=2\sum _{i}\Gamma _{ik}^{i}}
Így a divergencia és a Laplace-operátor:
d
i
v
a
→
=
∑
i
∂
i
a
i
+
∑
i
,
j
Γ
j
i
j
a
i
=
∑
i
∂
i
a
i
+
∑
i
1
g
(
∂
i
g
)
a
i
=
∑
i
1
g
∂
i
(
g
a
i
)
{\displaystyle {\begin{aligned}\mathrm {div} \,{\vec {a}}&=\sum _{i}\partial _{i}a^{i}+\sum _{i,j}\Gamma _{ji}^{j}a^{i}=\sum _{i}\partial _{i}a^{i}+\sum _{i}{\frac {1}{\sqrt {g}}}(\partial _{i}{\sqrt {g}})a^{i}=\sum _{i}{\frac {1}{\sqrt {g}}}\partial _{i}({\sqrt {g}}a^{i})\end{aligned}}}
Δ
Φ
=
∑
i
∂
i
g
i
j
∂
j
Φ
+
∑
i
,
j
,
k
Γ
k
i
k
g
i
j
∂
j
Φ
=
∑
i
∂
i
g
i
j
∂
j
Φ
+
∑
i
,
j
1
g
(
∂
i
g
)
g
i
j
∂
j
Φ
=
∑
i
,
j
1
g
∂
i
(
g
g
i
j
∂
j
Φ
)
{\displaystyle {\begin{aligned}\Delta \Phi &=\sum _{i}\partial _{i}g^{ij}\partial _{j}\Phi +\sum _{i,j,k}\Gamma _{ki}^{k}g^{ij}\partial _{j}\Phi =\sum _{i}\partial _{i}g^{ij}\partial _{j}\Phi +\sum _{i,j}{\frac {1}{\sqrt {g}}}(\partial _{i}{\sqrt {g}})g^{ij}\partial _{j}\Phi =\sum _{i,j}{\frac {1}{\sqrt {g}}}\partial _{i}({\sqrt {g}}\,g^{ij}\partial _{j}\Phi )\end{aligned}}}
Koordinátafüggetlen divergencia [ szerkesztés ] A divergencia koordinátafüggetlen ábrázolása a következő forrássűrűséget vezeti be:
div
F
→
=
lim
Δ
V
→
0
1
Δ
V
∮
∂
(
Δ
V
)
d
A
→
⋅
F
→
{\displaystyle \operatorname {div} {\vec {F}}=\lim _{\Delta V\to 0}{\frac {1}{\Delta V}}\oint \limits _{\partial (\Delta V)}\!\mathrm {d} {\vec {A}}\cdot {\vec {F}}}
ahol
Δ
V
{\displaystyle \Delta V}
d
A
→
⋅
F
→
{\displaystyle \mathrm {d} {\vec {A}}\cdot {\vec {F}}}
∂
(
Δ
V
)
{\displaystyle \partial (\Delta V)}
r
→
=
(
u
0
1
,
u
0
2
,
u
0
3
)
{\displaystyle {\vec {r}}=(u_{0}^{1},u_{0}^{2},u_{0}^{3})}
b
→
i
Δ
u
i
=
e
→
i
h
i
Δ
u
i
{\displaystyle {\vec {b}}_{i}\Delta u^{i}={\vec {e}}_{i}h_{i}\Delta u^{i}}
u
i
{\displaystyle u^{i}}
u
i
∈
I
i
:=
[
u
0
i
,
u
0
i
+
Δ
u
i
]
{\displaystyle u^{i}\in I^{i}:=[u_{0}^{i},u_{0}^{i}+\Delta u^{i}]}
h
i
Δ
u
i
{\displaystyle h_{i}\Delta u^{i}}
e
→
i
{\displaystyle {\vec {e}}_{i}}
Δ
V
=
|
det
[
b
→
1
,
b
→
2
,
b
→
3
]
|
Δ
u
1
Δ
u
2
Δ
u
3
=
g
Δ
u
1
Δ
u
2
Δ
u
3
{\displaystyle \Delta V=\left|\det[{\vec {b}}_{1},{\vec {b}}_{2},{\vec {b}}_{3}]\right|\Delta u^{1}\Delta u^{2}\Delta u^{3}={\sqrt {g}}\,\Delta u^{1}\Delta u^{2}\Delta u^{3}}
A paralelepipedont az
u
i
=
u
0
i
=
c
o
n
s
t
{\displaystyle u^{i}=u_{0}^{i}=\mathrm {const} }
u
i
=
u
0
i
+
Δ
u
i
=
c
o
n
s
t
{\displaystyle u^{i}=u_{0}^{i}+\Delta u^{i}=\mathrm {const} }
u
i
=
u
0
i
=
c
o
n
s
t
{\displaystyle u^{i}=u_{0}^{i}=\mathrm {const} }
d
A
→
i
=
±
∑
j
,
k
=
1
3
ϵ
i
j
k
b
→
j
×
b
→
k
d
u
j
d
u
k
=
±
∑
j
,
k
=
1
3
ϵ
i
j
k
g
b
→
i
d
u
j
d
u
k
{\displaystyle {\text{d}}{\vec {A}}^{i}=\pm \sum _{j,k=1}^{3}\epsilon _{ijk}{\vec {b}}_{j}\times {\vec {b}}_{k}\,{\text{d}}u^{j}{\text{d}}u^{k}=\pm \sum _{j,k=1}^{3}\epsilon _{ijk}{\sqrt {g}}\,{\vec {b}}^{\ i}\,{\text{d}}u^{j}{\text{d}}u^{k}}
és a
F
→
=
∑
l
F
l
b
→
l
{\displaystyle {\vec {F}}=\sum _{l}F^{l}{\vec {b}}_{l}}
d
A
→
i
⋅
F
→
=
±
∑
j
,
k
,
l
=
1
3
ϵ
i
j
k
g
F
l
b
→
i
⋅
b
→
l
⏟
δ
l
i
d
u
j
d
u
k
=
±
∑
j
,
k
=
1
3
ϵ
i
j
k
g
F
i
d
u
j
d
u
k
{\displaystyle \mathrm {d} {\vec {A}}^{i}\cdot {\vec {F}}=\pm \sum _{j,k,l=1}^{3}\epsilon _{ijk}{\sqrt {g}}\,F^{l}\underbrace {{\vec {b}}^{\ i}\cdot {\vec {b}}_{l}} _{\delta _{l}^{i}}\,{\text{d}}u^{j}{\text{d}}u^{k}=\pm \sum _{j,k=1}^{3}\epsilon _{ijk}{\sqrt {g}}\,F^{i}\,{\text{d}}u^{j}{\text{d}}u^{k}}
így a
u
1
=
u
0
1
{\displaystyle u^{1}=u_{0}^{1}}
−
d
A
→
1
{\displaystyle -\mathrm {d} {\vec {A}}^{\,1}}
−
d
A
→
1
{\displaystyle -\mathrm {d} {\vec {A}}^{\,1}}
Φ
1
a
=
∫
(
u
2
,
u
3
)
∈
I
2
×
I
3
[
−
d
A
→
1
⋅
F
→
]
(
u
0
1
,
u
2
,
u
3
)
=
∫
u
0
2
u
0
2
+
Δ
u
2
d
u
2
∫
u
0
3
u
0
3
+
Δ
u
3
d
u
3
[
−
g
F
1
]
(
u
0
1
,
u
2
,
u
3
)
≈
[
−
g
F
1
]
(
u
0
1
,
u
0
2
,
u
0
3
)
Δ
u
2
Δ
u
3
{\displaystyle {\begin{aligned}\Phi _{1a}&=\int \limits _{(u^{2},u^{3})\in I^{2}\times I^{3}}\!\left[-\mathrm {d} {\vec {A}}^{\,1}\cdot {\vec {F}}\right]_{(u_{0}^{1},u^{2},u^{3})}=\int \limits _{u_{0}^{2}}^{u_{0}^{2}+\Delta u^{2}}\!\mathrm {d} u^{2}\int \limits _{u_{0}^{3}}^{u_{0}^{3}+\Delta u^{3}}\!\mathrm {d} u^{3}\left[-{\sqrt {g}}\,F^{1}\right]_{(u_{0}^{1},u^{2},u^{3})}\\&\approx \left[-{\sqrt {g}}\,F^{1}\right]_{(u_{0}^{1},u_{0}^{2},u_{0}^{3})}\Delta u^{2}\Delta u^{3}\end{aligned}}}
és a
u
1
=
u
0
1
+
Δ
u
1
{\displaystyle u^{1}=u_{0}^{1}+\Delta u^{1}}
Φ
1
b
=
∫
(
u
2
,
u
3
)
∈
I
2
×
I
3
[
d
A
→
1
⋅
F
→
]
(
u
0
1
+
Δ
u
1
,
u
2
,
u
3
)
=
∫
u
0
2
u
0
2
+
Δ
u
2
d
u
2
∫
u
0
3
u
0
3
+
Δ
u
3
d
u
3
[
g
F
1
]
(
u
0
1
+
Δ
u
1
,
u
2
,
u
3
)
≈
[
g
F
1
]
(
u
0
1
+
Δ
u
1
,
u
0
2
,
u
0
3
)
Δ
u
2
Δ
u
3
≈
[
g
F
1
]
(
u
0
1
,
u
0
2
,
u
0
3
)
Δ
u
2
Δ
u
3
+
[
∂
g
F
1
∂
u
1
]
(
u
0
1
,
u
0
2
,
u
0
3
)
Δ
u
1
Δ
u
2
Δ
u
3
{\displaystyle {\begin{aligned}\Phi _{1b}&=\int \limits _{(u^{2},u^{3})\in I^{2}\times I^{3}}\!\left[\mathrm {d} {\vec {A}}^{\,1}\cdot {\vec {F}}\right]_{(u_{0}^{1}+\Delta u^{1},u^{2},u^{3})}=\int \limits _{u_{0}^{2}}^{u_{0}^{2}+\Delta u^{2}}\!\mathrm {d} u^{2}\int \limits _{u_{0}^{3}}^{u_{0}^{3}+\Delta u^{3}}\!\mathrm {d} u^{3}\left[{\sqrt {g}}\,F^{1}\right]_{(u_{0}^{1}+\Delta u^{1},u^{2},u^{3})}\\&\approx \left[{\sqrt {g}}\,F^{1}\right]_{(u_{0}^{1}+\Delta u^{1},u_{0}^{2},u_{0}^{3})}\Delta u^{2}\Delta u^{3}\approx \left[{\sqrt {g}}\,F^{1}\right]_{(u_{0}^{1},u_{0}^{2},u_{0}^{3})}\Delta u^{2}\Delta u^{3}+\left[{\frac {\partial {\sqrt {g}}\,F^{1}}{\partial u^{1}}}\right]_{(u_{0}^{1},u_{0}^{2},u_{0}^{3})}\Delta u^{1}\Delta u^{2}\Delta u^{3}\end{aligned}}}
itt az integrandust az
(
u
0
1
,
u
0
2
,
u
0
3
)
{\displaystyle (u_{0}^{1},u_{0}^{2},u_{0}^{3})}
Δ
u
i
{\displaystyle \Delta u^{i}}
Φ
1
=
Φ
1
a
+
Φ
1
b
=
[
∂
g
F
1
∂
u
1
]
(
u
0
1
,
u
0
2
,
u
0
3
)
Δ
u
1
Δ
u
2
Δ
u
3
{\displaystyle \Phi _{1}=\Phi _{1a}+\Phi _{1b}=\left[{\frac {\partial {\sqrt {g}}\,F^{1}}{\partial u^{1}}}\right]_{(u_{0}^{1},u_{0}^{2},u_{0}^{3})}\Delta u^{1}\Delta u^{2}\Delta u^{3}}
A többi koordinátára hasonlóan:
1
Δ
V
∮
∂
(
Δ
V
)
d
A
→
⋅
F
→
=
1
Δ
V
∑
i
=
1
3
Φ
i
=
1
g
Δ
u
1
Δ
u
2
Δ
u
3
∑
i
=
1
3
∂
g
F
i
∂
u
i
Δ
u
1
Δ
u
2
Δ
u
3
=
1
g
∑
i
=
1
3
∂
g
F
i
∂
u
i
{\displaystyle {\frac {1}{\Delta V}}\oint \limits _{\partial (\Delta V)}\!\mathrm {d} {\vec {A}}\cdot {\vec {F}}={\frac {1}{\Delta V}}\sum _{i=1}^{3}\Phi _{i}={\frac {1}{{\sqrt {g}}\,\Delta u^{1}\Delta u^{2}\Delta u^{3}}}\sum _{i=1}^{3}{\frac {\partial {\sqrt {g}}\,F^{i}}{\partial u^{i}}}\Delta u^{1}\Delta u^{2}\Delta u^{3}={\frac {1}{\sqrt {g}}}\sum _{i=1}^{3}{\frac {\partial {\sqrt {g}}\,F^{i}}{\partial u^{i}}}}
így a divergencia a természetes
F
i
{\displaystyle F^{i}}
F
~
i
{\displaystyle {\tilde {F}}^{i}}
div
F
→
=
1
g
∑
i
∂
i
g
F
i
=
1
g
∑
i
∂
i
g
F
~
i
/
h
i
{\displaystyle \operatorname {div} {\vec {F}}={\frac {1}{\sqrt {g}}}\sum _{i}\partial _{i}{\sqrt {g}}\,F^{i}={\frac {1}{\sqrt {g}}}\sum _{i}\partial _{i}{\sqrt {g}}\,{\tilde {F}}^{i}/h_{i}}
Ortogonális koordinátákban:
div
F
→
=
1
h
1
h
2
h
3
∑
i
∂
i
h
1
h
2
h
3
h
i
F
~
i
{\displaystyle \operatorname {div} {\vec {F}}={\frac {1}{h_{1}h_{2}h_{3}}}\sum _{i}\partial _{i}{\frac {h_{1}h_{2}h_{3}}{h_{i}}}{\tilde {F}}^{i}}
Koordinátafüggetlen rotáció [ szerkesztés ] A rotáció koordinátafüggetlen definíciója:
(
rot
F
→
)
⋅
n
^
=
lim
Δ
A
→
0
1
Δ
A
∮
∂
(
Δ
A
)
F
→
⋅
d
r
→
{\displaystyle (\operatorname {rot} {\vec {F}})\cdot {\hat {n}}=\lim _{\Delta A\to 0}{\frac {1}{\Delta A}}\oint \limits _{\partial (\Delta A)}\!{\vec {F}}\cdot \mathrm {d} {\vec {r}}}
ahol
Δ
A
{\displaystyle \Delta A}
n
^
{\displaystyle {\hat {n}}}
∫
d
r
→
⋅
F
→
{\displaystyle \int \mathrm {d} {\vec {r}}\cdot {\vec {F}}}
∂
(
Δ
A
)
{\displaystyle \partial (\Delta A)}
A továbbiakban egy
n
^
=
b
→
3
/
|
b
→
3
|
{\displaystyle {\hat {n}}={\vec {b}}^{\;3}/|{\vec {b}}^{\;3}|}
(
rot
F
→
)
⋅
n
^
=
∑
i
=
1
3
(
rot
F
→
)
i
b
→
i
⋅
b
→
3
|
b
→
3
|
=
(
rot
F
→
)
3
1
|
b
→
3
|
{\displaystyle (\operatorname {rot} {\vec {F}})\cdot {\hat {n}}=\sum _{i=1}^{3}(\operatorname {rot} {\vec {F}})^{i}{\vec {b}}_{i}\cdot {\frac {{\vec {b}}^{\;3}}{|{\vec {b}}^{\;3}|}}=(\operatorname {rot} {\vec {F}})^{3}{\frac {1}{|{\vec {b}}^{\;3}|}}}
Legyen
Δ
A
{\displaystyle \Delta A}
r
→
=
(
u
0
1
,
u
0
2
,
u
0
3
)
{\displaystyle {\vec {r}}=(u_{0}^{1},u_{0}^{2},u_{0}^{3})}
b
→
1
Δ
u
1
{\displaystyle {\vec {b}}_{1}\Delta u^{1}}
b
→
2
Δ
u
2
{\displaystyle {\vec {b}}_{2}\Delta u^{2}}
Δ
A
=
|
b
→
1
Δ
u
1
×
b
→
2
Δ
u
2
|
=
g
|
b
→
3
|
Δ
u
1
Δ
u
2
{\displaystyle \Delta A=|{\vec {b}}_{1}\Delta u^{1}\times {\vec {b}}_{2}\Delta u^{2}|={\sqrt {g}}\,|{\vec {b}}^{\;3}|\,\Delta u^{1}\Delta u^{2}}
Az integráció ennek a paralelogrammának az éleit járja körbe:
[
u
0
1
,
u
0
2
]
→
d
r
→
=
b
→
1
d
u
1
γ
1
[
u
0
1
+
Δ
u
1
,
u
0
2
]
→
d
r
→
=
b
→
2
d
u
2
γ
2
[
u
0
1
+
Δ
u
1
,
u
0
2
+
Δ
u
2
]
→
d
r
→
=
b
→
1
d
u
1
γ
3
[
u
0
1
,
u
0
2
+
Δ
u
2
]
→
d
r
→
=
b
→
2
d
u
2
γ
4
[
u
0
1
,
u
0
2
]
{\displaystyle [u_{0}^{1},u_{0}^{2}]{\xrightarrow[{\mathrm {d} {\vec {r}}={\vec {b}}_{1}\mathrm {d} u^{1}}]{\gamma _{1}}}[u_{0}^{1}+\Delta u^{1},u_{0}^{2}]{\xrightarrow[{\mathrm {d} {\vec {r}}={\vec {b}}_{2}\mathrm {d} u^{2}}]{\gamma _{2}}}[u_{0}^{1}+\Delta u^{1},u_{0}^{2}+\Delta u^{2}]{\xrightarrow[{\mathrm {d} {\vec {r}}={\vec {b}}_{1}\mathrm {d} u^{1}}]{\gamma _{3}}}[u_{0}^{1},u_{0}^{2}+\Delta u^{2}]{\xrightarrow[{\mathrm {d} {\vec {r}}={\vec {b}}_{2}\mathrm {d} u^{2}}]{\gamma _{4}}}[u_{0}^{1},u_{0}^{2}]}
Ha
F
→
=
∑
i
=
1
3
F
i
b
→
i
{\displaystyle {\vec {F}}=\sum _{i=1}^{3}F_{i}{\vec {b}}^{\,\,i}}
F
→
⋅
d
r
→
=
F
1
d
u
1
{\displaystyle {\vec {F}}\cdot \mathrm {d} {\vec {r}}=F_{1}\,\mathrm {d} u^{1}}
γ
1
{\displaystyle \gamma _{1}}
γ
3
{\displaystyle \gamma _{3}}
F
→
⋅
d
r
→
=
F
2
d
u
2
{\displaystyle {\vec {F}}\cdot \mathrm {d} {\vec {r}}=F_{2}\,\mathrm {d} u^{2}}
γ
2
{\displaystyle \gamma _{2}}
γ
4
{\displaystyle \gamma _{4}}
Az 1 és 3 út menti integrálok összefoglalva:
∫
γ
1
+
γ
3
F
→
⋅
d
r
→
=
∫
u
0
1
u
0
1
+
Δ
u
1
[
F
1
]
(
u
1
,
u
0
2
,
u
0
3
)
d
u
1
+
∫
u
0
1
+
Δ
u
1
u
0
1
[
F
1
]
(
u
1
,
u
0
2
+
Δ
u
2
,
u
0
3
)
d
u
1
=
∫
u
0
1
u
0
1
+
Δ
u
1
(
[
F
1
]
(
u
1
,
u
0
2
,
u
0
3
)
−
[
F
1
]
(
u
1
,
u
0
2
+
Δ
u
2
,
u
0
3
)
)
d
u
1
{\displaystyle {\begin{aligned}\int _{\gamma _{1}+\gamma _{3}}\!{\vec {F}}\cdot \mathrm {d} {\vec {r}}&=\int \limits _{u_{0}^{1}}^{u_{0}^{1}+\Delta u^{1}}\!\left[F_{1}\right]_{(u^{1},u_{0}^{2},u_{0}^{3})}\mathrm {d} u^{1}+\int \limits _{u_{0}^{1}+\Delta u^{1}}^{u_{0}^{1}}\!\left[F_{1}\right]_{(u^{1},u_{0}^{2}+\Delta u^{2},u_{0}^{3})}\mathrm {d} u^{1}\\&=\int \limits _{u_{0}^{1}}^{u_{0}^{1}+\Delta u^{1}}\!\left(\left[F_{1}\right]_{(u^{1},u_{0}^{2},u_{0}^{3})}-\left[F_{1}\right]_{(u^{1},u_{0}^{2}+\Delta u^{2},u_{0}^{3})}\right)\mathrm {d} u^{1}\end{aligned}}}
Ha az integrandust az
(
u
0
1
,
u
0
2
,
u
0
3
)
{\displaystyle (u_{0}^{1},u_{0}^{2},u_{0}^{3})}
Δ
u
1
{\displaystyle \Delta u^{1}}
u
0
1
{\displaystyle u_{0}^{1}}
u
1
{\displaystyle u^{1}}
∫
γ
1
+
γ
3
F
→
⋅
d
r
→
≈
∫
u
0
1
u
0
1
+
Δ
u
1
(
−
[
∂
F
1
∂
u
2
]
(
u
0
1
,
u
0
2
,
u
0
3
)
Δ
u
2
)
d
u
1
=
−
[
∂
F
1
∂
u
2
]
(
u
0
1
,
u
0
2
,
u
0
3
)
Δ
u
2
Δ
u
1
{\displaystyle \int _{\gamma _{1}+\gamma _{3}}\!{\vec {F}}\cdot \mathrm {d} {\vec {r}}\approx \int \limits _{u_{0}^{1}}^{u_{0}^{1}+\Delta u^{1}}\!\left(-\left[{\frac {\partial F_{1}}{\partial u^{2}}}\right]_{(u_{0}^{1},u_{0}^{2},u_{0}^{3})}\Delta u^{2}\right)\mathrm {d} u^{1}=-\left[{\frac {\partial F_{1}}{\partial u^{2}}}\right]_{(u_{0}^{1},u_{0}^{2},u_{0}^{3})}\Delta u^{2}\Delta u^{1}}
Analóg módon, a 2 és a 4 út menti integrálra adódik, hogy:
∫
γ
2
+
γ
4
F
→
⋅
d
r
→
=
∫
u
0
2
u
0
2
+
Δ
u
2
(
[
F
2
]
(
u
0
1
+
Δ
u
1
,
u
2
,
u
0
3
)
−
[
F
2
]
(
u
0
1
,
u
2
,
u
0
3
)
)
⏟
≈
[
∂
F
2
∂
u
1
]
(
u
0
1
,
u
0
2
,
u
0
3
)
Δ
u
1
d
u
2
≈
[
∂
F
2
∂
u
1
]
(
u
0
1
,
u
0
2
,
u
0
3
)
Δ
u
1
Δ
u
2
{\displaystyle {\begin{aligned}\int _{\gamma _{2}+\gamma _{4}}\!{\vec {F}}\cdot \mathrm {d} {\vec {r}}&=\int \limits _{u_{0}^{2}}^{u_{0}^{2}+\Delta u^{2}}\!\underbrace {\left(\left[F_{2}\right]_{(u_{0}^{1}+\Delta u^{1},u^{2},u_{0}^{3})}-\left[F_{2}\right]_{(u_{0}^{1},u^{2},u_{0}^{3})}\right)} _{\approx \left[{\frac {\partial F_{2}}{\partial u^{1}}}\right]_{(u_{0}^{1},u_{0}^{2},u_{0}^{3})}\Delta u^{1}}\mathrm {d} u^{2}\approx \left[{\frac {\partial F_{2}}{\partial u^{1}}}\right]_{(u_{0}^{1},u_{0}^{2},u_{0}^{3})}\Delta u^{1}\Delta u^{2}\end{aligned}}}
Összevetve a cirkuláció
u
3
=
u
0
3
{\displaystyle u^{3}=u_{0}^{3}}
Δ
A
{\displaystyle \Delta A}
∮
∂
(
Δ
A
)
F
→
⋅
d
r
→
≈
[
∂
F
2
∂
u
1
−
∂
F
1
∂
u
2
]
(
u
0
1
,
u
0
2
,
u
0
3
)
Δ
u
1
Δ
u
2
{\displaystyle \oint \limits _{\partial (\Delta A)}\!{\vec {F}}\cdot \mathrm {d} {\vec {r}}\approx \left[{\frac {\partial F_{2}}{\partial u^{1}}}-{\frac {\partial F_{1}}{\partial u^{2}}}\right]_{(u_{0}^{1},u_{0}^{2},u_{0}^{3})}\Delta u^{1}\Delta u^{2}}
Δ
u
1
,
Δ
u
2
→
0
{\displaystyle \Delta u^{1},\Delta u^{2}\to 0}
(
u
0
1
,
u
0
2
,
u
0
3
)
{\displaystyle (u_{0}^{1},u_{0}^{2},u_{0}^{3})}
(
rot
F
→
)
3
1
|
b
→
3
|
=
lim
Δ
A
→
0
1
g
|
b
→
3
|
Δ
u
1
Δ
u
2
[
∂
F
2
∂
u
1
−
∂
F
1
∂
u
2
]
Δ
u
1
Δ
u
2
⟹
(
rot
F
→
)
3
=
1
g
[
∂
1
F
2
−
∂
2
F
1
]
{\displaystyle (\operatorname {rot} {\vec {F}})^{3}{\frac {1}{|{\vec {b}}^{\;3}|}}=\lim _{\Delta A\to 0}{\frac {1}{{\sqrt {g}}\,|{\vec {b}}^{\;3}|\,\Delta u^{1}\Delta u^{2}}}\left[{\frac {\partial F_{2}}{\partial u^{1}}}-{\frac {\partial F_{1}}{\partial u^{2}}}\right]\Delta u^{1}\Delta u^{2}\quad \implies \quad (\operatorname {rot} {\vec {F}})^{3}={\frac {1}{\sqrt {g}}}\left[\partial _{1}F_{2}-\partial _{2}F_{1}\right]}
Hasonló eredményeket kaphatunk a többi koordinátára is a koordináták ciklikus cseréjével. Így a rotáció azzal, hogy:
E
i
j
k
=
ε
i
j
k
/
g
{\displaystyle {\mathcal {E}}^{ijk}=\varepsilon ^{ijk}/{\sqrt {g}}}
(
rot
F
→
)
i
=
1
g
∑
j
k
ε
i
j
k
∂
j
F
k
⟹
rot
F
→
=
∑
i
j
k
b
→
i
E
i
j
k
∂
j
F
k
{\displaystyle \left(\operatorname {rot} {\vec {F}}\right)^{i}={\frac {1}{\sqrt {g}}}\sum _{jk}\varepsilon ^{ijk}\partial _{j}\,F_{k}\quad \implies \quad \operatorname {rot} {\vec {F}}=\sum _{ijk}{\vec {b}}_{i}{\mathcal {E}}^{ijk}\partial _{j}\,F_{k}}
A természetes
F
k
{\displaystyle F_{k}}
F
n
{\displaystyle F^{n}}
F
k
=
∑
n
g
k
n
F
n
{\displaystyle F_{k}=\sum _{n}g_{kn}F^{n}}
F
n
=
F
~
n
/
h
n
{\displaystyle F^{n}={\tilde {F}}^{n}/h_{n}}
b
→
i
=
h
i
e
→
i
{\displaystyle {\vec {b}}_{i}=h_{i}{\vec {e}}_{i}}
Ha a koordináták ortogonálisak, akkor
g
k
n
=
h
k
2
δ
k
n
{\displaystyle g_{kn}=h_{k}^{2}\delta _{kn}}
F
k
=
h
k
2
F
k
{\displaystyle F_{k}=h_{k}^{2}F^{k}}
g
=
h
1
h
2
h
3
{\displaystyle {\sqrt {g}}=h_{1}h_{2}h_{3}}
F
~
k
{\displaystyle {\tilde {F}}^{k}}
F
k
=
h
k
F
~
k
{\displaystyle F_{k}=h_{k}{\tilde {F}}^{k}}
rot
F
→
=
1
h
1
h
2
h
3
∑
i
j
k
h
i
e
→
i
ε
i
j
k
∂
j
(
h
k
F
~
k
)
{\displaystyle \operatorname {rot} {\vec {F}}={\frac {1}{h_{1}h_{2}h_{3}}}\sum _{ijk}h_{i}{\vec {e}}_{i}\varepsilon ^{ijk}\partial _{j}\,(h_{k}{\tilde {F}}^{k})}
A rotáció mint antiszimmetrikus tenzor [ szerkesztés ] A rotáció képletében feltűnnek a
∇
i
a
j
−
∇
j
a
i
{\displaystyle \nabla _{i}a_{j}-\nabla _{j}a_{i}}
∇
i
a
j
−
∇
j
a
i
=
∂
i
a
j
−
Γ
i
j
k
a
k
−
∂
j
a
i
+
Γ
j
i
k
a
k
=
∂
i
a
j
−
∂
j
a
i
⟺
∑
i
,
k
ϵ
i
j
k
Γ
i
k
l
=
−
∑
i
,
k
ϵ
i
j
k
Γ
i
k
l
=
0
{\displaystyle \nabla _{i}a_{j}-\nabla _{j}a_{i}=\partial _{i}a_{j}-\Gamma _{ij}^{k}a_{k}-\partial _{j}a_{i}+\Gamma _{ji}^{k}a_{k}=\partial _{i}a_{j}-\partial _{j}a_{i}\quad \iff \quad \sum _{i,k}\epsilon ^{ijk}\Gamma _{ik}^{l}=-\sum _{i,k}\epsilon ^{ijk}\Gamma _{ik}^{l}=0}
Ez a mennyiség egy másodfokú antiszimmetrikus tenzort ábrázol, a
a
→
{\displaystyle {\vec {a}}}
Példák görbevonalú koordináta-rendszerekre [ szerkesztés ] Ortogonális koordináta-rendszerek [ szerkesztés ]
ρ
≥
0
,
0
≤
ϕ
<
2
π
,
−
∞
<
z
<
∞
{\displaystyle \rho \geq 0\,,\quad 0\leq \phi <2\pi \,,\quad -\infty <z<\infty }
x
=
ρ
cos
ϕ
,
y
=
ρ
sin
ϕ
,
z
=
z
{\displaystyle x=\rho \cos \phi \,,\quad y=\rho \sin \phi \,,\quad z=z}
r
≥
0
,
0
≤
θ
≤
π
,
0
≤
ϕ
<
2
π
{\displaystyle r\geq 0\,,\quad 0\leq \theta \leq \pi \,,\quad 0\leq \phi <2\pi }
x
=
r
sin
θ
cos
ϕ
,
y
=
r
sin
θ
sin
ϕ
,
z
=
r
cos
θ
{\displaystyle x=r\sin \theta \cos \phi \,,\quad y=r\sin \theta \sin \phi \,,\quad z=r\cos \theta }
−
∞
<
u
<
∞
,
v
≥
0
,
−
∞
<
z
<
∞
{\displaystyle -\infty <u<\infty \,,\quad v\geq 0\,,\quad -\infty <z<\infty }
x
=
(
u
2
−
v
2
)
/
2
,
y
=
u
v
,
z
=
z
{\displaystyle x=(u^{2}-v^{2})/2\,,\quad y=uv\,,\quad z=z}
u
≥
0
,
v
≥
0
,
0
≤
ϕ
<
2
π
{\displaystyle u\geq 0\,,\quad v\geq 0\,,\quad 0\leq \phi <2\pi }
x
=
u
v
cos
ϕ
,
y
=
u
v
sin
ϕ
,
z
=
(
u
2
−
v
2
)
/
2
{\displaystyle x=uv\cos \phi \,,\quad y=uv\sin \phi \,,\quad z=(u^{2}-v^{2})/2}
ξ
≥
0
,
0
≤
ϕ
<
2
π
,
−
∞
<
z
<
∞
{\displaystyle \xi \geq 0\,,\quad 0\leq \phi <2\pi \,,\quad -\infty <z<\infty }
x
=
a
ch
ξ
cos
ϕ
,
y
=
a
sh
ξ
sin
ϕ
,
z
=
z
{\displaystyle x=a\operatorname {ch} \xi \cos \phi \,,\quad y=a\operatorname {sh} \xi \sin \phi \,,\quad z=z}
ξ
≥
0
,
0
≤
θ
≤
π
,
0
≤
ϕ
<
2
π
{\displaystyle \xi \geq 0\,,\quad 0\leq \theta \leq \pi \,,\quad 0\leq \phi <2\pi }
x
=
a
sh
ξ
sin
θ
cos
ϕ
,
y
=
a
sh
ξ
sin
θ
sin
ϕ
,
z
=
a
ch
ξ
cos
θ
{\displaystyle x=a\operatorname {sh} \xi \sin \theta \cos \phi \,,\quad y=a\operatorname {sh} \xi \sin \theta \sin \phi \,,\quad z=a\operatorname {ch} \xi \cos \theta }
ξ
≥
0
,
−
π
/
2
≤
ϑ
≤
π
/
2
,
0
≤
ϕ
<
2
π
{\displaystyle \xi \geq 0\,,\quad -\pi /2\leq \vartheta \leq \pi /2\,,\quad 0\leq \phi <2\pi }
x
=
a
ch
ξ
cos
ϑ
cos
ϕ
,
y
=
a
ch
ξ
cos
ϑ
sin
ϕ
,
z
=
a
sh
ξ
sin
ϑ
{\displaystyle x=a\operatorname {ch} \xi \cos \vartheta \cos \phi \,,\quad y=a\operatorname {ch} \xi \cos \vartheta \sin \phi \,,\quad z=a\operatorname {sh} \xi \sin \vartheta }
0
≤
u
<
2
π
,
−
∞
<
v
<
∞
,
−
∞
<
z
<
∞
{\displaystyle 0\leq u<2\pi \,,\quad -\infty <v<\infty \,,\quad -\infty <z<\infty }
x
=
a
sh
v
ch
v
−
cos
u
,
y
=
a
sin
u
ch
v
−
cos
u
,
z
=
z
{\displaystyle x={\frac {a\operatorname {sh} v}{\operatorname {ch} v-\cos u}}\,,\quad y={\frac {a\sin u}{\operatorname {ch} v-\cos u}}\,,\quad z=z}
x
2
a
2
−
λ
+
y
2
b
2
−
λ
+
z
2
c
2
−
λ
=
1
,
λ
<
c
2
<
b
2
<
a
2
x
2
a
2
−
μ
+
y
2
b
2
−
μ
+
z
2
c
2
−
μ
=
1
,
c
2
<
μ
<
b
2
<
a
2
x
2
a
2
−
ν
+
y
2
b
2
−
ν
+
z
2
c
2
−
ν
=
1
,
c
2
<
b
2
<
ν
<
a
2
{\displaystyle {\begin{aligned}{\frac {x^{2}}{a^{2}-\lambda }}+{\frac {y^{2}}{b^{2}-\lambda }}+{\frac {z^{2}}{c^{2}-\lambda }}&=1\ ,\quad \lambda <c^{2}<b^{2}<a^{2}\\{\frac {x^{2}}{a^{2}-\mu }}+{\frac {y^{2}}{b^{2}-\mu }}+{\frac {z^{2}}{c^{2}-\mu }}&=1\ ,\quad c^{2}<\mu <b^{2}<a^{2}\\{\frac {x^{2}}{a^{2}-\nu }}+{\frac {y^{2}}{b^{2}-\nu }}+{\frac {z^{2}}{c^{2}-\nu }}&=1\ ,\quad c^{2}<b^{2}<\nu <a^{2}\end{aligned}}}
Nem ortogonális koordináta-rendszer [ szerkesztés ] Alternatív elliptikus hengerkoordináták:
(
ξ
,
ϕ
,
z
)
{\displaystyle (\xi ,\phi ,z)}
ξ
≥
0
,
0
≤
ϕ
<
2
π
,
−
∞
<
z
<
∞
{\displaystyle \xi \geq 0\,,\quad 0\leq \phi <2\pi \,,\quad -\infty <z<\infty }
x
=
a
ξ
cos
ϕ
,
y
=
b
ξ
sin
ϕ
,
z
=
z
{\displaystyle x=a\xi \cos \phi \,,\quad y=b\xi \sin \phi \,,\quad z=z}
Differenciálgeometria [ szerkesztés ] A görbe vonalú koordináták egyik hagyományos alkalmazását a differenciálgeometriában találjuk meg, speciálisan differenciálható sokaságok atlaszaiban. A következőkben összefüggéseket vezetünk le a differenciálformák kalkulusához, amelyek ezen számítások alapján koordinátafüggetlenül ábrázolhatók.
Legyen
M
{\displaystyle M}
n
{\displaystyle n}
ω
{\displaystyle \omega }
k
{\displaystyle k}
p
∈
M
{\displaystyle p\in M}
ω
p
{\displaystyle \omega _{p}}
k
{\displaystyle k}
T
p
M
{\displaystyle T_{p}M}
ω
p
{\displaystyle \omega _{p}}
lineáris funkcionál , ami vektormező
k
{\displaystyle k}
ω
p
:
T
p
M
×
…
×
T
p
M
⏟
k
-szor
→
R
{\displaystyle \omega _{p}\colon \underbrace {T_{p}M\times \ldots \times T_{p}M} _{k{\text{-szor}}}\to \mathbb {R} }
Itt
ω
p
{\displaystyle \omega _{p}}
Λ
k
(
T
p
∗
M
)
=
T
p
∗
M
∧
…
∧
T
p
∗
M
{\displaystyle \Lambda ^{k}(T_{p}^{*}M)=T_{p}^{*}M\wedge \ldots \wedge T_{p}^{*}M}
Λ
0
(
T
∗
M
)
=
C
∞
(
M
,
R
)
{\displaystyle \Lambda ^{0}(T^{*}M)=C^{\infty }(M,\mathbb {R} )}
Λ
1
(
T
∗
M
)
=
T
∗
M
{\displaystyle \Lambda ^{1}(T^{*}M)=T^{*}M}
M
{\displaystyle M}
k
{\displaystyle k}
Λ
k
(
T
∗
M
)
=
⨆
p
∈
M
Λ
k
(
T
p
∗
M
)
{\displaystyle \textstyle \Lambda ^{k}(T^{*}M)=\bigsqcup _{p\in M}\Lambda ^{k}(T_{p}^{*}M)}
Ω
k
(
M
)
{\displaystyle \Omega ^{k}(M)}
A tenzoranalízisben
ω
p
{\displaystyle \omega _{p}}
k
{\displaystyle k}
k
{\displaystyle k}
Differenciálformák: ábrázolás koordinátákkal [ szerkesztés ] Legyen
U
{\displaystyle U}
M
{\displaystyle M}
(
U
,
x
)
{\displaystyle (U,x)}
(
x
1
,
…
,
x
n
)
{\displaystyle (x^{1},\ldots ,x^{n})}
p
∈
U
{\displaystyle p\in U}
{
b
→
i
∣
i
=
1
,
…
n
}
=
{
∂
i
≡
∂
∂
x
i
∣
i
=
1
,
…
n
}
{\displaystyle \left\{{\vec {b}}_{i}\mid i=1,\ldots n\right\}=\left\{\partial _{i}\equiv {\frac {\partial }{\partial x^{i}}}\mid i=1,\ldots n\right\}}
a
T
p
M
{\displaystyle T_{p}M}
{
b
→
i
∣
i
=
1
,
…
n
}
=
{
d
x
i
∈
Ω
1
M
∣
i
=
1
,
…
n
}
{\displaystyle \left\{{\vec {b}}^{\ i}\mid i=1,\ldots n\right\}=\left\{\mathrm {d} x^{i}\in \Omega ^{1}M\mid i=1,\ldots n\right\}}
a hozzá tartozó duális bázis. A dualitást
d
x
i
∂
j
=
δ
j
i
{\displaystyle \mathrm {d} x^{i}\,\partial _{j}=\delta _{j}^{i}}
T
p
∗
M
=
Λ
1
(
T
p
∗
M
)
⊂
Ω
1
M
{\displaystyle T_{p}^{*}M=\Lambda ^{1}(T_{p}^{*}M)\subset \Omega ^{1}M}
T
p
M
{\displaystyle T_{p}M}
d
x
i
{\displaystyle \mathrm {d} x^{i}}
k
{\displaystyle k}
∧
{\displaystyle \wedge }
d
x
i
∧
d
x
j
{\displaystyle \mathrm {d} x^{i}\wedge \mathrm {d} x^{j}}
k
{\displaystyle k}
{
d
x
i
1
∧
…
∧
d
x
i
k
∈
Ω
k
M
∣
1
≤
i
1
<
…
<
i
k
≤
n
}
{\displaystyle \{\mathrm {d} x^{i_{1}}\wedge \ldots \wedge \mathrm {d} x^{i_{k}}\in \Omega ^{k}M\mid 1\leq i_{1}<\ldots <i_{k}\leq n\}}
a
T
p
∗
M
{\displaystyle T_{p}^{*}M}
Λ
k
(
T
p
∗
M
)
{\displaystyle \Lambda ^{k}(T_{p}^{*}M)}
ω
∈
Ω
k
(
M
)
{\displaystyle \omega \in \Omega ^{k}(M)}
(
U
,
x
)
{\displaystyle (U,x)}
ω
=
∑
1
≤
i
1
<
…
<
i
k
≤
n
w
i
1
,
…
,
i
k
(
x
)
d
x
i
1
∧
…
∧
d
x
i
k
{\displaystyle \omega =\sum _{1\leq i_{1}<\ldots <i_{k}\leq n}w_{i_{1},\ldots ,i_{k}}(x)\,\mathrm {d} x^{i_{1}}\wedge \ldots \wedge \mathrm {d} x^{i_{k}}}
Például egy 2-forma:
ω
=
∑
1
≤
i
<
j
≤
n
w
i
j
(
x
)
d
x
i
∧
d
x
j
=
∑
1
≤
i
<
j
≤
n
w
i
j
(
x
)
(
d
x
i
⊗
d
x
j
−
d
x
j
⊗
d
x
i
)
{\displaystyle \omega =\sum _{1\leq i<j\leq n}w_{ij}(x)\,\mathrm {d} x^{i}\wedge \mathrm {d} x^{j}=\sum _{1\leq i<j\leq n}w_{ij}(x)\,\left(\mathrm {d} x^{i}\otimes \mathrm {d} x^{j}-\mathrm {d} x^{j}\otimes \mathrm {d} x^{i}\right)}
ami megfelel egy másodfokú antiszimmetrikus kovariáns tenzormezőnek. Az
n
=
3
{\displaystyle n=3}
ω
=
∑
i
,
j
=
1
i
<
j
3
w
i
j
(
x
)
d
x
i
∧
d
x
j
=
w
12
(
x
)
d
x
1
∧
d
x
2
+
w
13
(
x
)
d
x
1
∧
d
x
3
+
w
23
(
x
)
d
x
2
∧
d
x
3
{\displaystyle \omega =\sum _{\underset {i<j}{i,j=1}}^{3}w_{ij}(x)\,\mathrm {d} x^{i}\wedge \mathrm {d} x^{j}=w_{12}(x)\,\mathrm {d} x^{1}\wedge \mathrm {d} x^{2}+w_{13}(x)\,\mathrm {d} x^{1}\wedge \mathrm {d} x^{3}+w_{23}(x)\,\mathrm {d} x^{2}\wedge \mathrm {d} x^{3}}
A skalár- és vektormezők kapcsolata a differenciálformákkal [ szerkesztés ] Differenciálható skalármezők esetén teljesül az azonosság: az
f
:
M
→
R
{\displaystyle f\colon \,M\to \mathbb {R} }
C
∞
(
M
,
R
)
=
Ω
0
M
{\displaystyle C^{\infty }(M,\mathbb {R} )=\Omega ^{0}M}
A következő izomorfiával egy
v
→
∈
C
∞
(
M
,
R
n
)
{\displaystyle {\vec {v}}\in C^{\infty }(M,\mathbb {R} ^{n})}
⟨
⋅
∣
⋅
⟩
{\displaystyle \left\langle \cdot \mid \cdot \right\rangle }
Einstein-féle összegkonvenciót is:
C
∞
(
M
,
R
n
)
⟶
≅
Ω
1
M
,
v
→
=
v
i
b
→
i
↦
⟨
v
→
∣
⋅
⟩
=
v
i
⟨
b
→
i
∣
⋅
⟩
=
v
i
d
x
i
{\displaystyle C^{\infty }(M,\mathbb {R} ^{n}){\overset {\cong }{\longrightarrow }}\Omega ^{1}M\ ,\quad {\vec {v}}=v_{i}{\vec {b}}^{\ i}\mapsto \left\langle {\vec {v}}\mid \cdot \right\rangle =v_{i}\left\langle {\vec {b}}^{\ i}\mid \cdot \right\rangle =v_{i}\mathrm {d} x^{i}}
A Hodge-Stern-operátorral egy skalármezőhöz hozzárendelhető egy
n
{\displaystyle n}
(
n
−
1
)
{\displaystyle (n-1)}
Művelet érintő- és koérintővektorok [ szerkesztés ] A flat, bé
♭
{\displaystyle \flat }
♯
{\displaystyle \sharp }
g
_
_
=
⟨
∂
i
∣
∂
j
⟩
d
x
i
⊗
d
x
j
{\displaystyle {\underline {\underline {g}}}=\left\langle \partial _{i}\mid \partial _{j}\right\rangle \mathrm {d} x^{i}\otimes \mathrm {d} x^{j}}
Riemann-metrika indukál, és az érintővektorokat a koérintővektorokra, illetve megfordítva képezik le:
♯
:
T
p
M
→
T
p
∗
M
,
v
i
e
i
→
↦
v
i
g
i
j
b
→
j
=
v
j
b
→
j
,
v
i
∂
i
↦
v
j
d
x
j
{\displaystyle \sharp :\,T_{p}M\to T_{p}^{*}M\ ,\quad v^{i}{\vec {e_{i}}}\mapsto v^{i}g_{ij}{\vec {b}}^{\ j}=v_{j}{\vec {b}}^{\ j}\ ,\quad v^{i}\partial _{i}\mapsto v_{j}\mathrm {d} x^{j}}
♭
:
T
p
∗
M
→
T
p
M
,
v
i
b
→
i
↦
v
i
g
i
j
b
→
j
=
v
j
b
→
j
,
v
i
d
x
i
↦
v
j
∂
j
{\displaystyle \flat :\,T_{p}^{*}M\to T_{p}M\ ,\quad v_{i}{\vec {b}}^{\ i}\mapsto v_{i}g^{ij}{\vec {b}}_{j}=v^{j}{\vec {b}}_{j}\ ,\quad v_{i}\mathrm {d} x^{i}\mapsto v^{j}\partial _{j}}
A tenzor notációban ez az indexek emelésének és süllyesztésének felel meg.
Az
n
{\displaystyle n}
k
{\displaystyle k}
n
−
k
{\displaystyle n-k}
Hodge-Stern-operátor :
∗
:
Ω
k
M
⟶
≅
Ω
n
−
k
M
{\displaystyle *:\,\Omega ^{k}M{\overset {\cong }{\longrightarrow }}\Omega ^{n-k}M}
Mindkét vektortér dimenziója
(
n
k
)
≡
(
n
n
−
k
)
{\displaystyle {\binom {n}{k}}\equiv {\binom {n}{n-k}}}
Három dimenzióban, azaz
n
=
3
{\displaystyle n=3}
Ω
0
M
↔
∗
Ω
3
M
,
ρ
↦
ρ
det
(
⋅
,
⋅
,
⋅
)
=
ρ
d
x
1
∧
d
x
2
∧
d
x
3
{\displaystyle \Omega ^{0}M{\overset {*}{\leftrightarrow }}\Omega ^{3}M\ ,\quad \rho \mapsto \rho \,\det(\cdot ,\cdot ,\cdot )=\rho \,\mathrm {d} x^{1}\wedge \mathrm {d} x^{2}\wedge \mathrm {d} x^{3}}
és egy 1-formához egy 2-formát
Ω
1
M
↔
∗
Ω
2
M
,
⟨
v
→
∣
⋅
⟩
=
v
i
d
u
i
↦
det
(
v
→
,
⋅
,
⋅
)
=
ϵ
j
k
i
v
i
d
x
j
∧
d
x
k
{\displaystyle \Omega ^{1}M{\overset {*}{\leftrightarrow }}\Omega ^{2}M\ ,\quad \left\langle {\vec {v}}\mid \cdot \right\rangle =v_{i}\mathrm {d} u^{i}\mapsto \det({\vec {v}},\cdot ,\cdot )=\epsilon _{\ jk}^{i}v_{i}\,\mathrm {d} x^{j}\wedge \mathrm {d} x^{k}}
Így egy differenciálható
a
→
{\displaystyle {\vec {a}}}
a
1
d
x
1
+
a
2
d
x
2
+
a
3
d
x
3
{\displaystyle a_{1}\mathrm {d} x^{1}+a_{2}\mathrm {d} x^{2}+a_{3}\mathrm {d} x^{3}}
a
1
d
x
2
∧
d
x
3
+
a
2
d
x
3
∧
d
x
1
+
a
3
d
x
1
∧
d
x
2
{\displaystyle a_{1}\,\mathrm {d} x^{2}\wedge \mathrm {d} x^{3}+a_{2}\,\mathrm {d} x^{3}\wedge \mathrm {d} x^{1}+a_{3}\,\mathrm {d} x^{1}\wedge \mathrm {d} x^{2}}
f
{\displaystyle f}
f
{\displaystyle f}
f
d
x
1
∧
d
x
2
∧
d
x
3
{\displaystyle f\,\mathrm {d} x^{1}\wedge \mathrm {d} x^{2}\wedge \mathrm {d} x^{3}}
Egy
k
{\displaystyle k}
(
k
+
1
)
{\displaystyle (k+1)}
De-Rham-komplexus . Két külső derivált láncolása identikus nullával. Ebből levezethetők a vektoranalízis integráltételei, a Stokes-tétel , Gauß integráltétele és a Green-tétel .
↑ William M. Boothby: An Introduction to Differential Manifolds and Riemannian Geometry . 2. überarbeitete Auflage. Academic Press, 2002.
↑ Gravitation . W.H. Freeman & Co (1973). ISBN 0-7167-0344-0 Günter Bärwolff : Höhere Mathematik für Naturwissenschaftler und Ingenieure. 2. Auflage, 1. korrigierte Nachdruck. Spektrum Akademischer Verlag, München u. a. 2009, ISBN 978-3-8274-1688-9 .Wolfgang Kühnel : Differentialgeometrie. Kurven – Flächen – Mannigfaltigkeiten. 4. überarbeitete Auflage. Vieweg, Wiesbaden 2008, ISBN 978-3-8348-0411-2 .Siegfried Kästner: Vektoren, Tensoren, Spinoren. Eine Einführung in den Tensorkalkül unter Berücksichtigung der physikalischen Anwendung. 2. verbesserte Auflage. Akademie-Verlag, Berlin 1964.
Murray R. Spiegel, Dennis Spellman, Seymour Lipschutz: Vector Analysis . Schaum’s Outlines. 2. Auflage. McGraw-Hill, 2009, ISBN 978-0-07-161545-7 .
Heinz Schade, Klaus Neemann: Tensoranalysis . 3. überarbeitete Auflage. de Gruyter, Berlin 2009, ISBN 978-3-11-020696-8 .
Klaus Jänich : Vektoranalysis . 5. Auflage. Springer-Verlag, Berlin 2005, ISBN 978-3-540-23741-9 .Ez a szócikk részben vagy egészben a Krummlinige Koordinaten



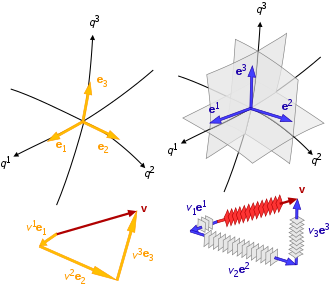
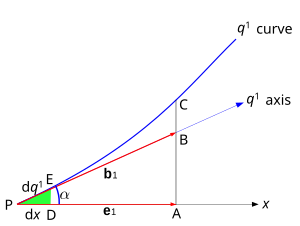






















































![{\displaystyle {\underline {\underline {J}}}={\frac {\partial (x_{1},x_{2},\ldots ,x_{n})}{\partial (u_{1},u_{2},\ldots ,u_{n})}}=\left({\begin{array}{cccc}\partial x_{1}/\partial u_{1}&\partial x_{1}/\partial u_{2}&\ldots &\partial x_{1}/\partial u_{n}\\\partial x_{2}/\partial u_{1}&\partial x_{2}/\partial u_{2}&\ldots &\partial x_{2}/\partial u_{n}\\\vdots &\vdots &&\vdots \\\partial x_{n}/\partial u_{1}&\partial x_{n}/\partial u_{2}&\ldots &\partial x_{n}/\partial u_{n}\end{array}}\right)=\left({\begin{array}{cccc}|&|&&|\\{\vec {b}}_{u_{1}}&{\vec {b}}_{u_{2}}&\ldots &{\vec {b}}_{u_{n}}\\|&|&&|\end{array}}\right)\equiv [{\vec {b}}_{u_{1}},{\vec {b}}_{u_{2}},\ldots ,{\vec {b}}_{u_{n}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5db6f62458e26ac98fdd91460f916361a1e2e9d)













![{\displaystyle {\underline {\underline {g}}}={\underline {\underline {J}}}^{T}{\underline {\underline {J}}}=[{\vec {b}}_{u_{1}},{\vec {b}}_{u_{2}},\ldots ,{\vec {b}}_{u_{n}}]^{T}[{\vec {b}}_{u_{1}},{\vec {b}}_{u_{2}},\ldots ,{\vec {b}}_{u_{n}}]=\left({\begin{array}{ccc}{\vec {b}}_{u_{1}}\cdot {\vec {b}}_{u_{1}}&\ldots &{\vec {b}}_{u_{1}}\cdot {\vec {b}}_{u_{n}}\\\vdots &&\vdots \\{\vec {b}}_{u_{n}}\cdot {\vec {b}}_{u_{1}}&\ldots &{\vec {b}}_{u_{n}}\cdot {\vec {b}}_{u_{n}}\end{array}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2994cd79d3472f88bd63a3429650105aeea0918b)







![{\displaystyle \det[{\vec {b}}_{u_{1}},{\vec {b}}_{u_{2}},\ldots ,{\vec {b}}_{u_{n}}]\equiv \det J=\pm {\sqrt {g}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f04da35a1146737d842ee177c802393fc72334e)
![{\displaystyle \det[{\vec {e}}_{u_{1}},{\vec {e}}_{u_{2}},\ldots ,{\vec {e}}_{u_{n}}]=\det[h_{u_{1}}^{-1}{\vec {b}}_{u_{1}},h_{u_{2}}^{-1}{\vec {b}}_{u_{2}},\ldots ,h_{u_{n}}^{-1}{\vec {b}}_{u_{n}}]={\frac {\det[{\vec {b}}_{u_{1}},{\vec {b}}_{u_{2}},\ldots ,{\vec {b}}_{u_{n}}]}{h_{u_{1}}h_{u_{2}}\cdots h_{u_{n}}}}={\frac {\pm {\sqrt {g}}}{h_{u_{1}}h_{u_{2}}\cdots h_{u_{n}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/913f59e132d536a875b3bd7cff792c4b72ab087c)














![{\displaystyle \det[{\vec {b}}_{u_{1}},{\vec {b}}_{u_{2}},\ldots ,{\vec {b}}_{u_{n}}]={\sqrt {g}}=h_{u_{1}}h_{u_{2}}\cdots h_{u_{3}}\quad \iff \quad \det[{\vec {e}}_{u_{1}},{\vec {e}}_{u_{2}},\ldots ,{\vec {e}}_{u_{n}}]=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8dbb2dc92ac48136ad6ea0125adb25375f97372)















![{\displaystyle f\colon \ V\rightarrow K,\ {\vec {v}}\mapsto f[{\vec {v}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b82ffe9599445d35cb42a01a11d4df655e54c0c7)
![{\displaystyle {\vec {e}}_{i}^{\,*}[{\vec {e}}_{j}]=\delta _{ij}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c0658fe3e59a7e6ca55acc312b2cac25c2e20a9)
![{\displaystyle \langle \cdot ,\cdot \rangle \colon \ V^{*}\times V\rightarrow K,\ \langle f,{\vec {v}}\rangle =f[{\vec {v}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cce9bc4bc47df72d50fc99372c7dedbf0fbe0a86)














![{\displaystyle [{\vec {b}}_{u_{1}}^{\ *},{\vec {b}}_{u_{2}}^{\ *},\ldots ,{\vec {b}}_{u_{n}}^{\ *}]^{T}[{\vec {b}}_{u_{1}},{\vec {b}}_{u_{2}},\ldots ,{\vec {b}}_{u_{n}}]={\underline {\underline {E}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/39efb2609f63076cc25f59679aa3972a36d881d6)
![{\displaystyle {\underline {\underline {J}}}=[{\vec {b}}_{u_{1}},{\vec {b}}_{u_{2}},\ldots ,{\vec {b}}_{u_{n}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02fd902ef5b6def82a959c51a8d1a13914666755)
![{\displaystyle {\underline {\underline {J}}}^{-1}=[{\vec {b}}_{u_{1}}^{\ *},{\vec {b}}_{u_{2}}^{\ *},\ldots ,{\vec {b}}_{u_{n}}^{\ *}]^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2265b4be2579759fba8e5395f7a6b6763d15d1e9)
![{\displaystyle \det[{\vec {b}}_{u_{1}}^{\ *},{\vec {b}}_{u_{2}}^{\ *},\ldots ,{\vec {b}}_{u_{n}}^{\ *}]^{T}=\det(J^{-1})={\frac {1}{\det(J)}}={\frac {1}{\sqrt {g}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8ef27f6bc11c9dfcc332b7cdb6784531b7f0e38)




































![{\displaystyle \epsilon _{ijk}=\det[{\vec {e}}_{x_{i}},{\vec {e}}_{x_{j}},{\vec {e}}_{x_{k}}]\equiv \det[{\vec {e}}_{x_{i}},{\vec {e}}_{x_{j}},{\vec {e}}_{x_{k}}]\ ,\quad {\mathcal {E}}_{ijk}=\det[{\vec {b}}_{u_{i}},{\vec {b}}_{u_{j}},{\vec {b}}_{u_{k}}]={\sqrt {g}}\,\epsilon _{ijk}\ ,\quad {\mathcal {E}}^{ijk}=\det[{\vec {b}}_{u_{i}}^{\ *},{\vec {b}}_{u_{j}}^{\ *},{\vec {b}}_{u_{k}}^{\ *}]={\frac {1}{\sqrt {g}}}\,\epsilon ^{ijk}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/635c4dbe75507c440b35338f2a0a30dd5781b4e0)
![{\displaystyle {\frac {\partial {\vec {a}}}{\partial u_{k}}}=\sum \limits _{i=1}^{n}{\frac {\partial \left(a_{u_{i}}{\vec {e}}_{u_{i}}\right)}{\partial u_{k}}}=\sum \limits _{i=1}^{n}{\left[{\frac {\partial a_{u_{i}}}{\partial u_{k}}}{\vec {e}}_{u_{i}}+a_{u_{i}}{\frac {\partial {\vec {e}}_{u_{i}}}{\partial u_{k}}}\right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f299be145e5e456967a8d7b8445a426b601502eb)
![{\displaystyle {\frac {\partial {\vec {a}}}{\partial u_{k}}}=\sum \limits _{i=1}^{n}{\frac {\partial \left({\tilde {a}}_{u_{i}}{\vec {b}}_{u_{i}}\right)}{\partial u_{k}}}=\sum \limits _{i=1}^{n}{\left[{\frac {\partial {\tilde {a}}_{u_{i}}}{\partial u_{k}}}{\vec {b}}_{u_{i}}+{\tilde {a}}_{u_{i}}{\frac {\partial {\vec {b}}_{u_{i}}}{\partial u_{k}}}\right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79406073ca48f4cc8ea78e5b60c76c60ef4fe4bd)







![{\displaystyle {\frac {\partial {\vec {a}}}{\partial u_{k}}}=\sum \limits _{i=1}^{n}\left[{\frac {\partial {\tilde {a}}_{u_{i}}}{\partial u_{k}}}{\vec {b}}_{u_{i}}+\sum _{j=1}^{n}{\tilde {a}}_{u_{i}}\Gamma _{ki}^{j}{\vec {b}}_{u_{j}}\right]=\sum \limits _{i=1}^{n}\left[{\frac {\partial {\tilde {a}}_{u_{i}}}{\partial u_{k}}}+\sum _{j=1}^{n}{\tilde {a}}_{u_{j}}\Gamma _{kj}^{i}\right]{\vec {b}}_{u_{i}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79dcb4820c2333c86b10ba0cabc46ad88da5eb9b)














![{\displaystyle L_{\vec {w}}{\vec {a}}\equiv [{\vec {w}},{\vec {a}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5d573f1ba8d995311797e7dd27a368b42ff27d2)










![{\displaystyle {\frac {\partial {\vec {a}}}{\partial u_{k}}}=\sum \limits _{i=1}^{n}{\frac {\partial \left({\tilde {a}}_{u_{i}}^{\,*}{\vec {b}}_{u_{i}}^{\ *}\right)}{\partial u_{k}}}=\sum \limits _{i=1}^{n}\left[{\frac {\partial {\tilde {a}}_{u_{i}}^{\,*}}{\partial u_{k}}}-\sum _{j}{\tilde {a}}_{u_{j}}^{\,*}\Gamma _{ki}^{j}\right]{\vec {b}}_{u_{i}}^{\,*}\quad \Longrightarrow \quad \nabla _{u_{k}}{\tilde {a}}_{u_{i}}^{\,*}={\frac {\partial {\tilde {a}}_{u_{i}}^{\,*}}{\partial u_{k}}}-\sum _{j=1}^{n}{\tilde {a}}_{u_{j}}^{\,*}\Gamma _{ki}^{j}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b7cf6dde8b9245a6031adc5894b7eb814852925)

![{\displaystyle \Gamma _{ij}^{k}=\left\{{\begin{array}{c}k\\ij\end{array}}\right\}\quad {\text{illetve}}\quad \Gamma _{ij,k}=\left[ij,k\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0aee4e0cb56fbef496415086a456d09d2d7a1888)





![{\displaystyle {\vec {v}}\times {\vec {w}}=\sum _{ijk}\epsilon _{ijk}v_{j}w_{k}{\vec {e}}_{i}^{\,*}=\sum _{ijk}\epsilon ^{ijk}v_{j}^{\,*}w_{k}^{\,*}{\vec {e}}_{i}\quad {\text{ahol}}\quad \epsilon _{ijk}=\epsilon ^{ijk}=\det[{\vec {e}}_{i},{\vec {e}}_{j},{\vec {e}}_{k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0baff8043d2f9e8e3eab27a5c6867a7e7e453135)
![{\displaystyle {\mathcal {E}}_{ijk}=\det[{\vec {b}}_{u_{i}},{\vec {b}}_{u_{j}},{\vec {b}}_{u_{k}}]={\sqrt {g}}\,\epsilon _{ijk}\ ,\quad {\mathcal {E}}^{ijk}=\det[{\vec {b}}_{u_{i}}^{\ *},{\vec {b}}_{u_{j}}^{\ *},{\vec {b}}_{u_{k}}^{\ *}]={\frac {1}{\sqrt {g}}}\,\epsilon ^{ijk}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c2764b7e12c0185447d36eaa08fd7eb0973afbf)





![{\displaystyle {\begin{aligned}{\mathcal {E}}_{ijk}:=\det \!\left[{\frac {\partial {\vec {r}}}{\partial u_{i}}},{\frac {\partial {\vec {r}}}{\partial u_{j}}},{\frac {\partial {\vec {r}}}{\partial u_{k}}}\right]&=\det \!{\Biggl [}\sum _{l}{\frac {\partial x_{l}}{\partial u_{i}}}\underbrace {\frac {\partial {\vec {r}}}{\partial x_{l}}} _{{\vec {e}}_{l}},\sum _{m}{\frac {\partial x_{m}}{\partial u_{j}}}\underbrace {\frac {\partial {\vec {r}}}{\partial x_{m}}} _{{\vec {e}}_{m}},\sum _{n}{\frac {\partial x_{n}}{\partial u_{k}}}\underbrace {\frac {\partial {\vec {r}}}{\partial x_{n}}} _{{\vec {e}}_{n}}{\Biggr ]}\\&=\sum _{l,m,n}{\frac {\partial x_{l}}{\partial u_{i}}}{\frac {\partial x_{m}}{\partial u_{j}}}{\frac {\partial x_{n}}{\partial u_{k}}}\underbrace {\det \!\left[{\vec {e}}_{l},{\vec {e}}_{m},{\vec {e}}_{n}\right]} _{\epsilon _{lmn}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c397ee851b09754aaf567507da0aace2558681c2)










![{\displaystyle {\sqrt {\tilde {g}}}={\sqrt {EG-F^{2}}}=\left|{\vec {b}}_{u_{1}}\times {\vec {b}}_{u_{2}}\right|=\det \left[{\vec {b}}_{u_{1}},{\vec {b}}_{u_{2}},{\hat {n}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a50ce1b4df653e35c9ce6b51e739f713e8b4d8f)











![{\displaystyle h_{\alpha \beta }=-{\vec {e}}_{\alpha }\cdot \partial _{\beta }{\hat {n}}=-\partial _{\beta }\underbrace {({\vec {e}}_{\alpha }\cdot {\hat {n}})} _{=0}+{\hat {n}}\cdot \partial _{\beta }{\vec {e}}_{\alpha }={\hat {n}}\cdot \partial _{\beta }{\vec {e}}_{\alpha }={\frac {1}{\sqrt {{\tilde {g}}^{\,}}}}\det \left[{\vec {b}}_{u_{1}},{\vec {b}}_{u_{2}},\partial _{\beta }{\vec {e}}_{\alpha }\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e193d43e01330afc9714d31b66506553109a66bb)





























![{\displaystyle {\text{d}}V=\left|{\text{d}}{\vec {r}}_{u_{1}}\cdot \left({\text{d}}{\vec {r}}_{u_{2}}\times {\text{d}}{\vec {r}}_{u_{3}}\right)\right|=\left|\det[{\text{d}}{\vec {r}}_{u_{1}},{\text{d}}{\vec {r}}_{u_{1}},{\text{d}}{\vec {r}}_{u_{3}}]\right|=\left|\det[{\vec {b}}_{u_{1}},{\vec {b}}_{u_{2}},{\vec {b}}_{u_{3}}]\right|{\text{d}}u_{1}{\text{d}}u_{2}{\text{d}}u_{3}=\left|{\sqrt {g}}\right|{\text{d}}u_{1}{\text{d}}u_{2}{\text{d}}u_{3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/391591bb604d4ba0eac4d6c1f33d4a86eb4f03bf)

![{\displaystyle {\text{d}}V=\left|\det[{\vec {e}}_{u_{1}},{\vec {e}}_{u_{2}},{\vec {e}}_{u_{3}}]\right|\left|h_{u_{1}}h_{u_{2}}h_{u_{3}}\right|{\text{d}}u_{1}{\text{d}}u_{2}{\text{d}}u_{3}=\left|{\sqrt {g}}\right|{\text{d}}u_{1}{\text{d}}u_{2}{\text{d}}u_{3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/56edf417c905ca98da059630fb3480a1a5859f86)








![{\displaystyle {\begin{aligned}{\vec {\nabla }}\cdot {\vec {a}}&={\frac {1}{h_{u_{1}}h_{u_{2}}h_{u_{3}}}}\sum _{j=1}^{3}{\frac {\partial }{\partial u_{j}}}\left({\frac {h_{u_{1}}h_{u_{2}}h_{u_{3}}}{h_{u_{j}}}}a_{u_{j}}\right)\\&={\frac {1}{h_{u_{1}}h_{u_{2}}h_{u_{3}}}}\left[{\frac {\partial }{\partial u_{1}}}\left(h_{u_{2}}h_{u_{3}}a_{u_{1}}\right)+{\frac {\partial }{\partial u_{2}}}\left(h_{u_{1}}h_{u_{3}}a_{u_{2}}\right)+{\frac {\partial }{\partial u_{3}}}\left(h_{u_{1}}h_{u_{2}}a_{u_{3}}\right)\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/462e86bf56f37042927523d352417dbb2351d0bd)

![{\displaystyle {\begin{aligned}\Delta \Phi &={\frac {1}{h_{u_{1}}h_{u_{2}}h_{u_{3}}}}\sum _{j=1}^{3}{\frac {\partial }{\partial u_{j}}}\left({\frac {h_{u_{1}}h_{u_{2}}h_{u_{3}}}{h_{u_{j}}^{2}}}{\frac {\partial \Phi }{\partial u_{j}}}\right)\\&={\frac {1}{h_{u_{1}}h_{u_{2}}h_{u_{3}}}}\left[{\frac {\partial }{\partial u_{1}}}\left({\frac {h_{u_{2}}h_{u_{3}}}{h_{u_{1}}}}{\frac {\partial \Phi }{\partial u_{1}}}\right)+{\frac {\partial }{\partial u_{2}}}\left({\frac {h_{u_{1}}h_{u_{3}}}{h_{u_{2}}}}{\frac {\partial \Phi }{\partial u_{2}}}\right)+{\frac {\partial }{\partial u_{3}}}\left({\frac {h_{u_{1}}h_{u_{2}}}{h_{u_{3}}}}{\frac {\partial \Phi }{\partial u_{3}}}\right)\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5afa5b918c8337645bef87ae4780bbc4d85f7fb)




















![{\displaystyle {\begin{aligned}\operatorname {div} {\underline {\underline {S}}}&=\sum _{i,j,k}\partial _{k}[S^{ij}\,{\vec {b}}_{i}\otimes {\vec {b}}_{j}]\cdot {\vec {b}}^{~k}=\sum _{i,j,k}\left[\nabla _{k}S^{ij}\right]{\vec {b}}_{i}\otimes \underbrace {{\vec {b}}_{j}\cdot {\vec {b}}^{~k}} _{\delta _{j}^{k}}=\sum _{i,k}\left[\nabla _{k}S^{ik}\right]{\vec {b}}_{i}\\&=\sum _{i,j,k}\partial _{k}[S_{i}^{~j}\,{\vec {b}}^{~i}\otimes {\vec {b}}_{j}]\cdot {\vec {b}}^{~k}=\sum _{i,j,k}\left[\nabla _{k}S_{i}^{~j}\right]{\vec {b}}^{~i}\otimes \underbrace {{\vec {b}}_{j}\cdot {\vec {b}}^{~k}} _{\delta _{j}^{k}}=\sum _{i,k}\left[\nabla _{k}S_{i}^{~k}\right]{\vec {b}}^{~i}\\&=\sum _{i,j,k}\partial _{k}[S_{~j}^{i}\,{\vec {b}}_{i}\otimes {\vec {b}}^{~j}]\cdot {\vec {b}}^{~k}=\sum _{i,j,k}\left[\nabla _{k}S_{~j}^{i}\right]{\vec {b}}_{i}\otimes \underbrace {{\vec {b}}^{~j}\cdot {\vec {b}}^{~k}} _{g^{jk}}=\sum _{i,k}\left[\nabla _{k}S^{ik}\right]{\vec {b}}_{i}\\&=\sum _{i,j,k}\partial _{k}[S_{ij}\,{\vec {b}}^{~i}\otimes {\vec {b}}^{~j}]\cdot {\vec {b}}^{~k}=\sum _{i,j,k}\left[\nabla _{k}S_{ij}\right]{\vec {b}}^{~i}\otimes \underbrace {{\vec {b}}^{~j}\cdot {\vec {b}}^{~k}} _{g^{jk}}=\sum _{i,k}\left[\nabla _{k}S_{i}^{~k}\right]{\vec {b}}^{~i}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0de855d4603967fec4d22dd592f8f7c2e7d11f5d)






























![{\displaystyle u^{i}\in I^{i}:=[u_{0}^{i},u_{0}^{i}+\Delta u^{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c440d0e7610b5446d22a50ad9dbd7d3e720bac08)


![{\displaystyle \Delta V=\left|\det[{\vec {b}}_{1},{\vec {b}}_{2},{\vec {b}}_{3}]\right|\Delta u^{1}\Delta u^{2}\Delta u^{3}={\sqrt {g}}\,\Delta u^{1}\Delta u^{2}\Delta u^{3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ab8e3a99276b491f660dfa7364f9f20037ac41e)







![{\displaystyle {\begin{aligned}\Phi _{1a}&=\int \limits _{(u^{2},u^{3})\in I^{2}\times I^{3}}\!\left[-\mathrm {d} {\vec {A}}^{\,1}\cdot {\vec {F}}\right]_{(u_{0}^{1},u^{2},u^{3})}=\int \limits _{u_{0}^{2}}^{u_{0}^{2}+\Delta u^{2}}\!\mathrm {d} u^{2}\int \limits _{u_{0}^{3}}^{u_{0}^{3}+\Delta u^{3}}\!\mathrm {d} u^{3}\left[-{\sqrt {g}}\,F^{1}\right]_{(u_{0}^{1},u^{2},u^{3})}\\&\approx \left[-{\sqrt {g}}\,F^{1}\right]_{(u_{0}^{1},u_{0}^{2},u_{0}^{3})}\Delta u^{2}\Delta u^{3}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c7b251feee03267407cf1b2af3f860d7db57cf1)

![{\displaystyle {\begin{aligned}\Phi _{1b}&=\int \limits _{(u^{2},u^{3})\in I^{2}\times I^{3}}\!\left[\mathrm {d} {\vec {A}}^{\,1}\cdot {\vec {F}}\right]_{(u_{0}^{1}+\Delta u^{1},u^{2},u^{3})}=\int \limits _{u_{0}^{2}}^{u_{0}^{2}+\Delta u^{2}}\!\mathrm {d} u^{2}\int \limits _{u_{0}^{3}}^{u_{0}^{3}+\Delta u^{3}}\!\mathrm {d} u^{3}\left[{\sqrt {g}}\,F^{1}\right]_{(u_{0}^{1}+\Delta u^{1},u^{2},u^{3})}\\&\approx \left[{\sqrt {g}}\,F^{1}\right]_{(u_{0}^{1}+\Delta u^{1},u_{0}^{2},u_{0}^{3})}\Delta u^{2}\Delta u^{3}\approx \left[{\sqrt {g}}\,F^{1}\right]_{(u_{0}^{1},u_{0}^{2},u_{0}^{3})}\Delta u^{2}\Delta u^{3}+\left[{\frac {\partial {\sqrt {g}}\,F^{1}}{\partial u^{1}}}\right]_{(u_{0}^{1},u_{0}^{2},u_{0}^{3})}\Delta u^{1}\Delta u^{2}\Delta u^{3}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa1230d1bd84dbb4c677198a4034d558efdc51dc)


![{\displaystyle \Phi _{1}=\Phi _{1a}+\Phi _{1b}=\left[{\frac {\partial {\sqrt {g}}\,F^{1}}{\partial u^{1}}}\right]_{(u_{0}^{1},u_{0}^{2},u_{0}^{3})}\Delta u^{1}\Delta u^{2}\Delta u^{3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44d56bbb205d59eda9a102c5e1185d06887ceeff)














![{\displaystyle [u_{0}^{1},u_{0}^{2}]{\xrightarrow[{\mathrm {d} {\vec {r}}={\vec {b}}_{1}\mathrm {d} u^{1}}]{\gamma _{1}}}[u_{0}^{1}+\Delta u^{1},u_{0}^{2}]{\xrightarrow[{\mathrm {d} {\vec {r}}={\vec {b}}_{2}\mathrm {d} u^{2}}]{\gamma _{2}}}[u_{0}^{1}+\Delta u^{1},u_{0}^{2}+\Delta u^{2}]{\xrightarrow[{\mathrm {d} {\vec {r}}={\vec {b}}_{1}\mathrm {d} u^{1}}]{\gamma _{3}}}[u_{0}^{1},u_{0}^{2}+\Delta u^{2}]{\xrightarrow[{\mathrm {d} {\vec {r}}={\vec {b}}_{2}\mathrm {d} u^{2}}]{\gamma _{4}}}[u_{0}^{1},u_{0}^{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3aade1d40f655007278827bbec87fd88f2ca6e5f)







![{\displaystyle {\begin{aligned}\int _{\gamma _{1}+\gamma _{3}}\!{\vec {F}}\cdot \mathrm {d} {\vec {r}}&=\int \limits _{u_{0}^{1}}^{u_{0}^{1}+\Delta u^{1}}\!\left[F_{1}\right]_{(u^{1},u_{0}^{2},u_{0}^{3})}\mathrm {d} u^{1}+\int \limits _{u_{0}^{1}+\Delta u^{1}}^{u_{0}^{1}}\!\left[F_{1}\right]_{(u^{1},u_{0}^{2}+\Delta u^{2},u_{0}^{3})}\mathrm {d} u^{1}\\&=\int \limits _{u_{0}^{1}}^{u_{0}^{1}+\Delta u^{1}}\!\left(\left[F_{1}\right]_{(u^{1},u_{0}^{2},u_{0}^{3})}-\left[F_{1}\right]_{(u^{1},u_{0}^{2}+\Delta u^{2},u_{0}^{3})}\right)\mathrm {d} u^{1}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82ae7db59f7bc73d1a0ba5711d5da04488b4e969)



![{\displaystyle \int _{\gamma _{1}+\gamma _{3}}\!{\vec {F}}\cdot \mathrm {d} {\vec {r}}\approx \int \limits _{u_{0}^{1}}^{u_{0}^{1}+\Delta u^{1}}\!\left(-\left[{\frac {\partial F_{1}}{\partial u^{2}}}\right]_{(u_{0}^{1},u_{0}^{2},u_{0}^{3})}\Delta u^{2}\right)\mathrm {d} u^{1}=-\left[{\frac {\partial F_{1}}{\partial u^{2}}}\right]_{(u_{0}^{1},u_{0}^{2},u_{0}^{3})}\Delta u^{2}\Delta u^{1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4fd9c7add8e7aa77e9e51e57dd74a5c897bbf9e1)
![{\displaystyle {\begin{aligned}\int _{\gamma _{2}+\gamma _{4}}\!{\vec {F}}\cdot \mathrm {d} {\vec {r}}&=\int \limits _{u_{0}^{2}}^{u_{0}^{2}+\Delta u^{2}}\!\underbrace {\left(\left[F_{2}\right]_{(u_{0}^{1}+\Delta u^{1},u^{2},u_{0}^{3})}-\left[F_{2}\right]_{(u_{0}^{1},u^{2},u_{0}^{3})}\right)} _{\approx \left[{\frac {\partial F_{2}}{\partial u^{1}}}\right]_{(u_{0}^{1},u_{0}^{2},u_{0}^{3})}\Delta u^{1}}\mathrm {d} u^{2}\approx \left[{\frac {\partial F_{2}}{\partial u^{1}}}\right]_{(u_{0}^{1},u_{0}^{2},u_{0}^{3})}\Delta u^{1}\Delta u^{2}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59b158ab8e8f79c8b66fec592668443dea4221ba)

![{\displaystyle \oint \limits _{\partial (\Delta A)}\!{\vec {F}}\cdot \mathrm {d} {\vec {r}}\approx \left[{\frac {\partial F_{2}}{\partial u^{1}}}-{\frac {\partial F_{1}}{\partial u^{2}}}\right]_{(u_{0}^{1},u_{0}^{2},u_{0}^{3})}\Delta u^{1}\Delta u^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97cf0e2454c320abc075f263d4416dfc6b9ecb62)

![{\displaystyle (\operatorname {rot} {\vec {F}})^{3}{\frac {1}{|{\vec {b}}^{\;3}|}}=\lim _{\Delta A\to 0}{\frac {1}{{\sqrt {g}}\,|{\vec {b}}^{\;3}|\,\Delta u^{1}\Delta u^{2}}}\left[{\frac {\partial F_{2}}{\partial u^{1}}}-{\frac {\partial F_{1}}{\partial u^{2}}}\right]\Delta u^{1}\Delta u^{2}\quad \implies \quad (\operatorname {rot} {\vec {F}})^{3}={\frac {1}{\sqrt {g}}}\left[\partial _{1}F_{2}-\partial _{2}F_{1}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e23c16251a83d91161e1d93e8084fbcb2a6708e)



























































































