Kvadratrix

A kvadratrix (triszektrix, Hippiász-görbe, Hippiász görbéje, Hippiász-féle kvadratrix, Hippiász-féle triszektrix, D(e)inosztratosz-féle kvadratrix stb.) a matematikában egy nevezetes síkgörbe, amelynek feltalálását az éliszi Hippiásznak (i. e. 460 körül – i. e. 400 körül) tulajdonítják.[1]
Nevezetessége abban áll, hogy egy, az euklideszi síkon rendelkezésre álló quadratrix segítségével - amint erre már az említett Hippiász, ill. később Deinosztratosz is rámutatott - megoldhatóak lennének a szögharmadolás (triszekció) és a körnégyszögesítés (kvadratúra) nevű, klasszikus és híres antik görög geometriai problémák. Minthogy azonban a görbe összes pontja nem szerkeszthető meg euklideszi módon, ezért a kvadratrix nem jelent „szabályos” megoldást. Közelítő jellegű megoldásra viszont alkalmas.
Története[szerkesztés]
A neves angol matematikatörténész, T. L. Heath szerint Hippiász i. e. 420 körül találhatta fel a görbét;[2] Hippiász műve azonban, amelyben leírta a kvadratrixot (ha egyáltalán létezett), nem maradt fenn.
Bizonyos jelek arra utalnak, hogy a rhodoszi Geminusnak még volt egy példánya ebből a műből, és az tartalmazta annak leírását, hogyan kell a görbét a szögfelosztáshoz és körnégyszögesítéshez felhasználni; ma már egy példányt sem ismerünk belőle.[3]
Azonban Papposz, a neves görög életrajzíró egyik műve (a Szünagogé, i. e. 340.; IV. könyv.) tárgyalja a görbe definícióját.
Teljesen bizonyos viszont, hogy Deinosztratosz ismerte a görbét, és felhasználta a – nem-euklideszi módon való – körnégyszögesítéshez.
Származtatása[szerkesztés]
A görbe elemi és eredeti származtatása[szerkesztés]
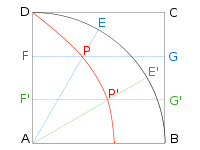

Legyen ABCD négyzet, az R = AB = AD sugárral az A körül írt negyedkörrel együtt.
- Tekintsük az AD helyzetből az AB helyzetbe egyenletesen (állandó sebességgel) forgó - a mellékelt ábrán az óramutatók járásával egyező módon járó, negatív forgásszöget leíró - sugarat! Legyen ennek helyzete a mozgás valamely t időpillanatában AE, pontosabban - mivel az E=E(t) pont függ a „t” időtől - AE(t)!
- Tekintsük továbbá az DC helyzetből a AB helyzetbe egyenletesen (állandó sebességgel) eltolt (tehát kezdeti helyzetével mindig párhuzamosan mozgó, a szomszédos oldalakra pedig mindig merőleges) négyzetoldalt (v. egyenest). Legyen ennek az egyenesnek a t időpontban metszéspontja az AD oldallal F(t), a BC oldallal G(t)!
Mozogjon továbbá az AD sugár és a CD egyenes(szakasz) úgy, hogy mozgásuk egyszerre kezdődjön és egyszerre is érjen véget!
Ez esetben a két mozgó alakzat, vagyis az AE sugár és a FG egyenes metszéspontjainak (P(t)) mértani helye épp a kvadratrix. Ez a metszéspont mellesleg mindig létezik (bár ennek bizonyításával sem a görögök, sem az utánuk jövők vélhetően nem foglalkoztak), és a származtató vonalak egyetlenegy helyzetét kivéve (a végsőt, amikor mindkettő, a sugár és az eltolt négyzetoldal, egybeesik az AB szakasszal), mindig egyértelmű. De ebben a „kivételes”, irreguláris helyzetben is definiálható, differenciálgeometriai módszerrel, a görbének olyan pontja az AB szakaszon), hogy azzal kiegészítve is egy folytonos és egyszerű görbét kapjunk (ld. még folytonos folytatás).
Bár megtévesztően másképp látszhat, a két mozgás nem ugyanolyan gyors (annak ellenére, hogy ugyanakkor kezdődik és ugyanakkor fejeződik be), hiszen az E pont jóval hosszabb utat tesz meg, mint az F és G pontok. Válasszuk időegységnek a lezajló mozgások időtartamát, ennek előnye, hogy ekkor az alakzatok által megtett út egyezik a sebességükkel:
- az E pont egységnyi idő alatt K utat tesz meg (K a negyedkör kerülete, R a sugarának hossza), ahol K = (2Rπ)/ 4 = Rπ/2
- az F és G pontok egységnyi idő alatt R utat tesznek meg,
tehát az E pont, ill. az AB sugár sebessége épp π/2-szerese az FG szakasz sebességének (azaz körülbelül 1,57-szorosa), adott időtartam alatt mindig ennyiszer nagyobb utat tesz meg a sugár köríven fekvő végpontja.
Az „irreguláris” pont[szerkesztés]
A görbének van egy „irreguláris” pontja, nevezetesen a t=1 időpillanatnak megfelelő pont (az I. ábrán a „legalsó”, az AB szakaszon lévő, betűjelölés nélküli, piros pont) a Hippiász-féle konstrukcióval nem kapható meg. Hippiász módszerével ugyanis a t=1 időpillanatban nem pontot kapnánk, hanem az egész AB szakaszt, hiszen e pillanatban a sugár már legördült az AB-szakasszá, és az eltolás is az AB-be vitte a DC-n átmenő négyzetoldalt, tehát az AE(1) = AB szakasz metszetét kellene az F(1)G(1) = AB szakasszal képezni, ami maga az AB szakasz.
Bizonyítható azonban, hogy az AB szakaszon pontosan egy olyan pont található, amely a P(t) metszéspontok halmazának (az összes 0≤t<1 értékre) az euklideszi síkon mint metrikus térben a torlódási pontja ; mégpedig az a P(1) := Q osztópont, amelyre AQ:AB = 2/π. Szemléletesen ez azt jelenti, hogy ha egyre inkább közeledünk a t=1 időpillanat felé, azaz a mozgás végéhez, akkor a Hippiász-féle görbe addigi pontjai egyre közelebb lesznek a Q ponthoz (ahogyan a II. ábrán ez látható).[5]
Ha a 0≤t<1 paraméterű görbepontokhoz hozzávesszük ezt a Q pontot, az I. ábrán látható folytonos, hagyományos értelemben vett görbét kapjuk.
Mivel a Q pont osztóviszonya a π reciprokának kétszerese, a kvadratrix Q pontját megszerkesztve a π hosszúságú szakasz is euklideszi módon megszerkeszthető lenne, amiből következne a körkvadratúra és a körrektifikáció megoldása. Valójában azonban éppenséggel a Q a kvadratrix egyik nem-szerkeszthető pontja. Emiatt a körrektifikációs és körkvadratálási szerkesztési feladatok a kvadratrix segítségével sem oldhatóak meg euklideszi módon, csak ha valamilyen más módszerrel sikerül megrajzolni a teljes kvadratrixot (azonban ez már nem euklideszi megoldás).
A görbe explicit képlete[szerkesztés]

Mai jelölésekkel Hippiász leírásából adódik a kvadratrix (ún. explicit) egyenlete, továbbá a paraméteres egyenletrendszere, ha az D pontba mint origóba olyan Descartes-féle ℜ koordináta-rendszert illesztünk, amelynek x-tengelye a DA, y-tengelye a DC egyenes.[6] koordináta-rendszer Ekkor ugyanis az F(t) pont a t időpillanatban éppen az x=tR (első) koordinátájú helyen tartózkodik, hiszen t idő alatt, ha sebessége R volt, épp ennyi utat tett meg. Tehát F(t)=(x,0)ℜ.
Ezalatt - az előző szakasz megállapításait és feltételeit (t∈[0;1]) figyelembe véve - az E(t) pont olyan φ szöggel fordul el D-ből, amelynek íve épp π/2-szer akkora, mint a G által megtett út, azaz x, tehát a szög íve xπ/2, ekkor viszont ívmértékben mérve úgy kapjuk e szöget, ha ívét osztjuk a sugár hosszával, ez a szög tehát éppen φ=xπ/2R rad nagyságú.
A tengelyekre merőlegesen levetítve az E(t) pontot, adódnak az E1=(0, e1)ℜ és E2=(e2,0)ℜ pontok. Ezekre érvényes - a szögfüggvények elemi definíciója szerint - AE1 = e1(t) = Rsin(φ) = E2E és E2A = R-e2(t) = Rcos(φ). A görbe definíciója szerint a P(t) kvadratrix-pont éppen az AE(t) egyenes(szakasz) (sugár) metszéspontja az x=x(t)=t egyenletű egyenessel (vagyis azzal, ami F(t)-ben merőlegesen metszi az x-tengelyt). A P(t) merőleges vetületei legyenek P1=(p1, 0)=(x,0) és P2=(0, f2)=(0,y), tehát f1(t)=x(t)=x és f2(t):=y(t)=y, ekkor hasonlóak a következő háromszögek:
Emiatt:
azaz
Tehát (y-t kifejezve, rendezve és egyszerűsítve, valamint behelyettesítve φ helyébe xπ/2R-t):
Ha meg akarunk felelni az ábra I. koordinátasík-negyedbe való korlátozottságának, akkor ki kell kötnünk még azt is, hogy x∈[0,R).
Megjegyzések:
- Diszkusszió: A fenti levezetés nem érvényes abban a helyzetben, amikor E2A = P2A = 0, vagyis amikor t=1, azaz ha x=R, azaz ha φ=π/2. Ebben a helyzetben a képleteknek sincs értelme, mivel a nevezőben a koszinusz nullává, így a tangens értelmezhetetlenné válik. Ezért szükséges nemcsak az x∈[0,R], hanem a szigorúbb x∈[0,R) kikötés. Vagyis a képlet az „irreguláris” pontra éppúgy nem érvényes, mint a Hippiász-féle definíció. Az ábrákon tulajdonképpen egy lyukas körrel kellene jelezni, hogy az AB oldalra eső pont valójában nem része a görbének. Mivel azonban a görbe folytonosan folytatható ebben a pontban,[7] túl nagy félreértés nem fenyeget.
- Más derékszögű koordináta-rendszerek: Néhány szerző (pl. Kürschák József) apró változtatásokkal tárgyalja a görbét, pl. a származtató mozgást „visszafelé játszva” tekinti a fent leírthoz képest. Ez azzal a didaktikai hátránnyal jár, hogy a görbe elsőként meghatározott pontja rögtön irreguláris. Mindenesetre, ugyanúgy adható explicit képlet a görbére, például, ha a koordináta-rendszer origóját a B pontba rögzítjük, x-tengelynek a BC egyenest, y-tengelynek a BA egyenest vesszük, akkor a görbét megadó képlet:
Paraméteres egyenletrendszer[szerkesztés]
Az explicit képletből egyenesen adódik a paraméteres egyenletrendszer.
ahol t∈[0;1). Ezt a kikötést elhagyva, a görbe kiterjesztése minden valós paraméterre, természetesen adódik (ld. id. szakasz).
Kiterjesztések[szerkesztés]
A paraméterektől az x=t helyettesítéssel megszabadulva, a kvadratrix egyenlete az adott Descartes-féle koordináta-rendszerben:
ahol R tetszőleges valós állandó.
 |
 |
Alkalmazások[szerkesztés]
A körnégyszögítés[szerkesztés]
A körnégyszögesítéshez - amint ezt Dinosztratosz és Papposz is megjegyezte - elegendő az irreguláris pont megszerkesztése. Sajnos ez éppenséggel egy nem szerkeszthető pont.[8] Ennélfogva a kvadratrix nem jelent megoldást az euklideszi szerkesztések szempontjából.
Jegyzetek[szerkesztés]
- ↑ Egyes matematikatörténészek kétségbe vonják, hogy a görbét feltaláló, Hippiász nevű geométer azonos az éliszi Hippiásszal, a neves szofistával, mondván, hogy az éliszi korában a matematika még nem érte el a görbe feltalálásához szükséges fejlettséget - de az antik görög és európai tudománytörténeti hagyomány nem kételkedik az éliszi szerzőségében. Ld. Hippias of Elis, The MacTutor History of Mathematics archive. Link beill. 2010. 02. 04.
- ↑ Heath, Thomas Little: A History of Greek Mathematics I. (Oxford, 1921).
- ↑ Hippias of Elis, The MacTutor History of Mathematics archive. Link beill. 2010. 02. 04.
- ↑ Pontosabb (tengelybeosztásos) animáció - ld. Xah Lee: Visual Dictionary Of Special Plane Curves/Quadratrix of Hippias
- ↑ Ld. Kürschák József: A körmérés története és elmélete; Mathematikai és Physikai Lapok, I. évf. (1892) / 1.-2., 3., és 5. sz., 1. sz. 40. o.
- ↑ Ez azért meglehetősen természetes választás, mert így az egyik származtató segédalakzat, a mozgó húr elmozdulása épp az x-koordináta, ráadásul a kapott végeredmény is meglehetősen egyszerű lesz. Felhívjuk a figyelmet, hogy az x-tengely így függőleges, az y-tengely pedig vízszintes, eltérően a szokásos hagyománytól. Az ábrát (+)90°-kal, az óramutató járásával ellentétesen forgatva, kapnánk a szokott koordináta-rendszert.
- ↑ Ld. fentebb.
- ↑ [1]
Hivatkozások[szerkesztés]
Lásd még[szerkesztés]
További irodalom[szerkesztés]
- Dr. Darvasi Gyula: Síkgeometriai alapszerkesztések betoló vonalzóval (II. rész). A matematika tanítása (módszertani folyóirat); XIX. évf. 3. sz. (2011). Mozaik Kiadó, Szeged; ISSN 1216-6650. 19-20. o.
További információk[szerkesztés]
- Gérard P. Michon: Final Answers - Planar Curves. A „Numericana” projekt honlapja. Link beill. 2010. 02. 04.
- Crockett Johnson: Hippias' Curve - a kvadratrix egy absztrakt festményen. A National Museum of American History (Az Amerikai Történelem Nemzeti Múzeuma) honlapjáról. Link beill. 2010. 02. 13.







