Kockakettőzés
| Ez a szócikk nem tünteti fel a független forrásokat, amelyeket felhasználtak a készítése során. Emiatt nem tudjuk közvetlenül ellenőrizni, hogy a szócikkben szereplő állítások helytállóak-e. Segíts megbízható forrásokat találni az állításokhoz! Lásd még: A Wikipédia nem az első közlés helye. |
A kocka megduplázása – az ún. déloszi probléma – egyike az antik görög matematikusok által vizsgált és megoldatlan geometriai szerkesztési feladatoknak. Eszerint egy olyan kocka élét kellene megszerkeszteni, amelynek térfogata kétszerese egy adott kocka térfogatának. E térbeli szerkesztés síkbeli rokona a négyzet megduplázása, ami euklideszi szerkesztéssel megoldható, azonban a kocka kétszerezése nem.
A déloszi jóslat[szerkesztés]
Több ókori forrás (Plutarkhosz, Eutokiosz, Eratoszthenész) is beszámol arról a mondáról, ami a problémát Délosz lakóihoz köti. Eszerint a délosziak Apollón Delphoiban működő jósdájához fordultak, amikor városukat a pestis megtámadta. Az orákulum szerint Apollón kocka alakú oltárát kell kétszeresére cserélni, hogy a járványtól megszabaduljanak. A valóságban a feladat a monda keletkezését megelőzően is foglalkoztatta a tudósokat. A régészeti leletek között figyeltek fel olyan szarkofágokra, dobozokra, ládákra, amelyeknél a belső üreg térfogata a tömb térfogatának fele, alakja ahhoz hasonló. Ez a kockakettőzésnél általánosabb megfogalmazása ennek a matematikai problémának.
A probléma analízise[szerkesztés]
A geometriai szerkesztések elméletének eredménye szerint azok a szerkesztési feladatok, amelyek analitikusan irreducibilis harmadfokú egyenlethez vezetnek, nem oldhatók meg euklideszi szerkesztéssel. A kockakettőzés ilyen, ami a következőképpen látható be:
Jelölje az adott kocka élét és a szerkesztendőét . A két kocka térfogatának aránya a kikötés szerint: . Ebből a következő harmadfokú egyenlet írható fel: , aminek megoldása . Az adott kocka oldalát egységnyinek választva a feladat az irreducibilis harmadfokú egyenlet pozitív valós gyökének, az hosszúságú szakasznak a megszerkesztését jelenti.
Már az i. e. 430-ban Khiosz szigetéről Athénba települt Hippokratész rájött, hogy probléma az folytonos arány ismeretlenjeinek megszerkesztésével oldható meg. Eljutott a probléma általánosításához, ami a kocka térfogatának arányú ( esetben az 1:2 arányú) megváltoztatását írja elő. Ez az egyenletekkel írható le, s megfogalmazva azt követeli meg, hogy az és közé két középarányost illesszünk be.


A probléma síkbeli megfelelőjének megoldását már ekkor ismerték. Ez a négyzet területének arányú arányú megnövelését tűzi ki feladatul, ami az aránypár megoldásával egyenértékű. A megoldást, a mértani közép szerkesztését az érettségizettek jól ismerik. A szerkesztést illusztráló ábrában látszik az a két derékszögű háromszög, aminek hasonlóságából a szerkesztés helyessége kiolvasható. A térbeli feladat az és szakaszok két középarányosát keresi. Ehhez három hasonló háromszögre van szükség, amelyeknek megfelelő oldalpárjai és .
A téma története[szerkesztés]
A feladatot az a kikötés teszi megoldhatatlanná, hogy a szerkesztéshez csak körzőt és vonalzót szabad használni (euklideszi szerkesztés). A történészek szerint legelőször a khioszi Hippokratész (i. e. 430 k.) foglalkozott a feladattal behatóbban, bár ebből sejteni lehet, hogy az korábban is ismert volt a tudományos világban. A megoldás keresésében szinte minden neves ókori matematikus részt vett: Arkhütasz (i. e. 390 k.), Platón (i. e. 390 k.), Eudoxosz (i. e. 370 k.), Menaekhmosz (i. e. 350 k.), Eratoszthenész (i. e. 240 k.), Nikomédész (i. e. 240 k.), Apollóniosz (i. e. 210 k.), Hérón (i. sz. 60 k.), Papposz (i. sz. 320 k.) neve áll a listán. Mint a többi nevezetes antik probléma (körnégyszögesítés, szögharmadolás, körosztás) megoldásához, a kockakettőzéshez is igénybe vettek magasabb rendű szerkesztést: speciális vonalzókat, rajzeszközöket, kúpszeleteket, görbéket. A megoldhatatlanságot az ókorban már sejtették, de bizonyítása csak az újkori matematikusoknak sikerült. Az európai reneszánsz, majd a felvilágosodás matematikusai (Pascal, Newton stb.) gazdagították a megoldások sorát. Néhány nevezetesebb szerkesztést (nem időrendben) bemutatunk.
 |
Arkhütasz (i. e. 390 k.) térbeli módszere a derékszögű koordinátákban az kúp, az henger és az tórusz áthatásának megszerkesztésével jut el a megoldáshoz. Ezeket a forgásfelületeket a síkban megszerkesztett keresztmetszetük térbe való kiemelésével, mozgatással szerkeszti meg. Kortársai bírálták, mert a tiszta matematikát a mechanikai mozgással „becsteleníti” meg. |
 |
 |
Platón (i. e. 390 k.) a szerkesztéshez csuklós-csapos szerkezetet konstruált. Lényegét az egyszerűsített ábra demonstrálja: a három hasonló háromszöget egy derékszög vonalzó és egy kereszt alakú „vonalzó” segítségével rajzoljuk meg. Az a és b szakaszok kijelölése után e keresztet úgy kell a fix derékszöghöz támasztva mozgatni, hogy az ábrán látható téglalap alakuljon ki. (Az eredeti eszközön ezt további sínekkel érték el.) |
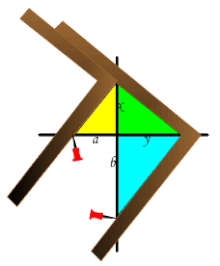 |
Arkhimédész (i. e. 250 k.) a Platón által készített szerkezet egyszerűsítésével kapta meg ugyanezt a megoldást. Az a és b szakaszokat egy merőleges egyenespárra mérte fel, majd két, egymáson csúsztatott és a felmért szakaszok végpontjába szúrt szegekhez támasztott derékszögű vonalzóval a két derékszöget a merőleges egyenesekhez igazította. |
 |
Menaikhmosz (i. e. 350 k.) kúpszeletek metszésével kapott több megoldást. Modern megfogalmazásban az parabolának a parabolával illetve az hiperbolával közös pontjait szerkesztette meg. Ezek a triviális mellett a pont. Később Descartes (i. sz. XVII. sz.) kimutatta, hogy ezek a pontok rajta vannak az körön, tehát az egyik görbe megrajzolása elegendő. |
 |
 |
Ugyancsak tőle származik az egyik legrégibb olyan megoldás, amit neuszisz szerkesztéssel hajthatunk végre. Az ábra a speciális esetre elvégzett szerkesztést mutatja be. Először egy szabályos és egy derékszögű háromszöget kell megszerkeszteni. A neuszisz szerkesztés eszközeit a helyükre tenni (pólus, direktrix), majd az N-vonalzót a kívánt helyzetbe hozni. A megoldás helyessége az ábra szakaszainak arányából kiolvasható: Teljesül az folytonosság, s ebből adódik az megoldás. |
 |
 |
Nikhomédész (i. e. 240 k.) a konhoisz felfedezésével új megoldásként rekonstruálja Menaikhmosz N-vonalzós szerkesztését. Csak a technika változik: a konhoisz megrajzolása után a megfelelő háromszögek és egyenesek körzős-vonalzós szerkesztéssel kaphatók. |
|
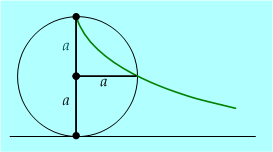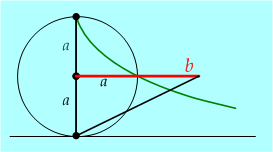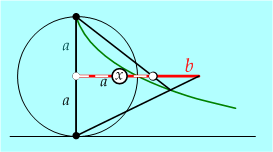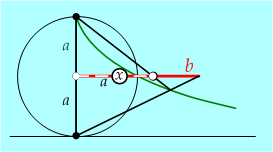
Dioklész (i. e. III. sz.) munkáit csak hivatkozásokból ismerjük. Eutokiosz az Arkhimédész-kommentárjában írta le két nevezetes szerkesztését, köztük a déloszi probléma megoldásához „felfedezett” cisszoiszt. A szerkesztés a cisszoisz megrajzolásával kezdődik. A kör sugara a megduplázandó kocka éle: . A szerkesztés további lépéseihez csak egy vonalzó kell. |

|
Eratoszthenész (i. e. 240 k.) mechanikus megoldása mutatja, hogy az i. e. III. sz. tudományos életében a déloszi probléma megoldása milyen fontos szerepet játszott, ugyanis a megoldás Ptolemaiosz isten-király templomában kőbe vésve olvasható, s ugyanott látható a szerkezet bronzból készült modellje. Ez két vonalzóból és három téglalap alakú lapocskából áll, amelyeken az egyik átlót is megjelölték. A lapokat az egyik vonalzón csúsztatva úgy kell elhelyezni a megoldáshoz, hogy a másik vonalzó mentén helyezkedjenek el a szomszédos lapok éleinek és átlóinak metszéspontjai. A háromszögek hasonlóságából igazolható a szerkesztés. |





![{\displaystyle x=a{\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd86ebf1dd6cbc2e8e126e08b23004f17a57c6e9)

![{\displaystyle x={\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c78fd4e8a5860369203e19242e3b8fc442b2e34)
















![{\displaystyle ({\sqrt[{3}]{4}};{\sqrt[{3}]{2}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/56ee1bdaa162d19057724307be26684b86c8f931)
