Kúpszelet


A matematikában a kúpszelet olyan síkgörbe, mely egy kúp, pontosabban egyenes körkúp és sík metszeteként jön létre. A kúpszeleteket már i. e. 200 körül felismerték és nevet adtak nekik, amikor is a pergai Apollóniosz tanulmányozta tulajdonságaikat.
A kúpszeletek fajtái[szerkesztés]
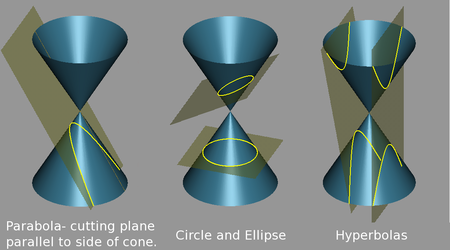
Két jól ismert kúpszelet a kör és az ellipszis. Ezek akkor jönnek létre, ha a kúpot metsző sík a kúp egyik alkotójával sem párhuzamos. A kör az ellipszis speciális esete akkor, ha a sík merőleges a kúp tengelyére. Ha a sík párhuzamos egy, a kúpot alkotóban érintő síkkal, a kúpszelet parabola. Végül, ha egy sík a dupla kúp mindkét palástját metszi, a görbe hiperbola.
Egy palást egy adott P pontján át egyetlen sík létezik, ami merőleges tengelyre, tehát a kúp felszínén egyetlen kör tartalmazza a P pontot. Az alkotó és a tengely által meghatározott síkra merőleges síkok P csúcsú kúpszeleteket metszenek ki, melyek között csak egy parabola van, ám végtelen sok az ellipszis és a hiperbola. A nem ilyen síkok végtelen sok ellipszist, parabolát vagy hiperbolát határoznak meg.
Elfajult esetek[szerkesztés]
Elfajult esetek akkor keletkeznek, ha a sík a kúp csúcsán megy keresztül, ebben az esetben az áthatási görbe ponttá, egyenessé, vagy két metsző egyenessé fajul, ezeket az eseteket gyakran nem sorolják a kúpszeletek közé.
(Még két elfajult eset létezik. Ezekhez az szükséges, hogy a kúp maga is elfajult legyen: vagyis, ha a kúpalkotó szöge a tengelyhez képest 90° vagy 0°. Ha ez a szög 90°, a kúp belseje által elfoglalt tér az egész háromdimenziós tér, míg a kúpon kívüli tér mindössze a csúcsponton átmenő, a tengelyre merőleges sík. Ugyanezt a síkot metszősíkként is választhatjuk, ekkor a kúpmetszet az egész sík. Másrészt, ha az alkotó és a tengely szöge 0° és a metszősík párhuzamos a kúptengellyel (de nem tartalmazza azt), nincs metszés.)
Kúpszeletek mint mértani helyek[szerkesztés]
Mindegyik kúpszeletet mértani helyként is lehet definiálni, vagyis minden P pontjuknak meghatározott tulajdonságaik vannak:
- Kör: , ahol C egy adott pont (a középpont) és r egy adott állandó távolság, (a sugár).
- Parabola: , ahol F egy adott pont (a fókusz) és L egy adott egyenes (a direktrix vagy vezéregyenes), mely nem tartalmazza az F fókuszt.
- Ellipszis: , ahol A,B két nem egybeeső pont (a fókuszok) és egy adott állandó távolság (a nagytengely)
- Hiperbola: , ahol A,B két nem egybeeső pont (a fókuszok) és egy adott távolság.
A projektív geometriában a kúpszeletek úgy definiálhatók, hogy mindegyik pontjuk egy adott ponttól (fókusz) és egy adott görbétől (direktrix) egyenlő távolságra van.
Excentricitás[szerkesztés]

A kört leszámítva az előbbiekkel ekvivalens definíciót adhatunk az excentricitás fogalmának segítségével: a kúpszelet azon pontok mértani helye, melyeknek egy egyenestől (a direktrixtől) és egy ponttól (a fókusztól) való távolságuk aránya állandó. Ez az arány az excentricitás, jele általában kis e.
Bizonyítás: A Dandelin-gömb által meghatározott kör síkja (Dandelin-sík) messe a kúpszelet síkját egy d egyenesben (ha a kúpszelet kör, akkor nem létezik ez az egyenes, minden más esetben igen). A kúpszelet tetszőleges P pontjára arány állandó, ahol F a kúpszelet azon fókusza, ahol a Dandelin-gömb érinti a síkot, D pedig P merőleges vetülete d-re.
ahol R a P-t tartalmazó alkotó és a Dandelin-gömb érintési pontja.
állandó, ahol M P merőleges vetülete a Dandelin-síkra, α a metsző sík és a kúp tengelye által bezárt szög, β a kúp félnyílásszöge.

Osztályozásuk az excentricitás nagysága szerint: ha 0<β<90°:
- ha α=90° akkor e=0 és a metszet egy kör vagy egy pont
- ha α>β akkor e<1 és a metszet egy ellipszis vagy egy pont
- ha α=β akkor e=1 és a metszet egy parabola vagy egy egyenes
- ha α<β akkor e>1 és a metszet egy hiperbola vagy egy metsző egyenespár
Descartes-koordináták[szerkesztés]
A Descartes-féle derékszögű koordináta-rendszerben egy kétváltozós kvadratikus egyenlet mindig kúpszeletet ír le, és az összes kúpszelet leírható ilyen módon. Az egyenlet alábbi alakú lesz:
ahol , , nem mind zéró.
ekkor:
- ha , az egyenlet ellipszist ír le (hacsak a kúp nem elfajult, például );
- ha és , az egyenlet kört ír le;
- ha , az egyenlet parabolát ír le;
- ha , az egyenlet hiperbolát ír le;
Megjegyzendő, hogy az A és B csak együtthatók, nem a nagytengely/kistengely hossza.
A koordináta-rendszer megfelelő megválasztásával a kanonikus formába írhatóak át a fenti egyenletek:
- Kör:
- Ellipszis:
- Parabola:
- Hiperbola:
Ezek az alakok szimmetrikusak az x tengelyre és kör, ellipszis és hiperbola esetén az y tengelyre is.
Kanonikus alakra hozás[szerkesztés]
A kanonikus alak kiszámításához először meg kell határozni a görbe típusát.
A másodrendű görbéket a következő alakban szokták megadni: , ahol x háromdimenziós vektor, és A háromszor hármas mátrix. Az ilyen alakban megadott görbéket is szokás kúpszeleteknek nevezni, pedig a képzetes ellipszis, párhuzamos egyenespár, párhuzamos képzetes egyenespár, valós-ideális egyenespár, kettős ideális egyenes nem áll elő kúp szeleteként. Ezek a koordináták homogén projektív koordináták, vagyis ugyanazt a vektort adja, mint .
A számításokhoz szükség van a következő mennyiségekre:
- Δ=det(A)
- A33=a bal felső 2 x 2-es mátrix determinánsa
- δ = bal felső 2 x 2-es mátrix nyoma
- Γ2 = δ2 − 4A33.
Centrális kúpszeletek[szerkesztés]
Ha A33 ≠ 0, akkor a kúpszelet centrális. Ekkor a projektív sík ideális egyenesének a kúpszeletre vett pólusa közönséges pont. Ha [A13,A23,A33] =(adj A)[0, 0, 1]T, akkor a kúpszelet középpontja (A13/A33). Ezt az origóba eltolva az A mátrix bal felső kétszer kettes része változatlan marad, míg a harmadik sor és oszlop az átlóban levő eleme kivételével kinullázódik, és az abban levő érték Δ/A33.
Ezután egy alkalmasan választott szöggel elforgatva már diagonális mátrixot kapunk, ahol a főátlóban levő értékek (u, v, 1), ahol is a − (δ ± Γ)·A33/2detA értékek egyike a v, és a másika az u.
- Ha u és v is pozitív, akkor a kúpszelet ellipszis, és a szokásos választás u ≤ v
- Ha u és v is negatív, akkor a kúpszelet képzetes ellipszis, és a szokásos választás u ≥ v
- Ha u és v előjele különböző, akkor a kúpszelet hiperbola, és a szokásos választás u > 0 > v.
Ellipszis esetén az ux2 + vy2 = 1 egyenlet átvihető a
alakba,
ahol
és
Képzetes ellipszis esetén a képletek ugyanezek.
Hiperbola esetén:
és
ahol
Ha A33=0, akkor a kúpszelet elfajuló. Ekkor a mátrix diagonalizálható, és a diagonális alakban az utolsó szám a nulla. Jelölje a másik két számot u és v! Ekkor a mátrix átskálázható, és konstans szorzó erejéig u és v értéke (δ±Γ)/2.
- Ha u és v előjele azonos, akkor a kúpszelet képzetes egyenespár valós metszésponttal, és a szokásos választás u ≥ v > 0, u−1 + v−1 = 1
- Ha u és v előjele különböző, akkor a kúpszelet valós metsző egyenespár, és a szokásos választás u > 0 > v; u ≤ |v|, u + |v| = 1
Képzetes egyenespár valós metszésponttal esetén a kanonikus alak az ellipsziséhez hasonló:
emiatt ezt a kúpszeletet pontellipszisnek is hívják.
Ebben az alakban
és
Valós metsző egyenespár esetén a kanonikus alak a hiperboláéhoz hasonló:
Ebben az alakban
és
Tengelyes kúpszeletek[szerkesztés]
Ha A33 = 0, akkor a kúpszelet tengelyes. Vezessük be a következő jelölést: Π = -δΔ. Hogyha A determinánsa nem nulla, akkor a kúpszelet parabola, egyébként pedig valamilyen egyenespár.
- Parabola esetén δ ≠0, Π > 0 és δ és Δ előjele különböző. A parabola mátrixa egy egy mellékátlós szimmetrikus mátrixba vihető át, ahonnan 1/δ-t kiemelve a mellékátló középső értéke 1, a többi
- Párhuzamos egyenespár esetén ki kell számítani az mennyiséget.
- Ha ez a mennyiség pozitív, akkor a kúpszelet képzetes párhuzamos egyenespár
- Ha ez a mennyiség negatív, akkor a kúpszelet valós párhuzamos egyenespár
- Ha ez a mennyiség nulla, akkor a kúpszelet kettős egyenes
A valós-ideális egyenespár kanonikus alakja x = 0, és a kettős ideális egyenes egyenlete már eleve kanonikus alakban van.
Polárkoordináták[szerkesztés]

A fókuszon átmenő, nagytengelyre merőleges húr felét általában l-lel jelölik. Ezt viszonyítják az a fél nagytengelyhez és a b fél kistengelyhez a , vagy képlettel.
Polárkoordinátákkal egy kúpszelet a következő egyenlettel adható meg, ha az origó az egyik fókuszban van, a másik pedig, ha létezik, az x tengely pozitív részén:
- .
Mint fent, körre e = 0, ellipszisre 0 < e < 1, parabolára e = 1 és hiperbolára e > 1.
Sajátságok[szerkesztés]
A kúpszeletek mindig „simák”. Ez pontosabban azt jelenti, hogy soha nincs inflexiós pontjuk, a vonalukban sehol nincs „öböl”. Ez fontos sok alkalmazásnál, például az aerodinamikában, ahol sima felületek szükségesek a lamináris áramlás biztosításához és a turbulencia elkerüléséhez.
Alkalmazások[szerkesztés]
A kúpszeletek fontosak az asztronómiában: két, egymást kölcsönösen vonzó test pályája kúpszelet, ha a tömegközéppontjukat nyugalomban lévőnek tekintjük. Ha visszatérő pályájuk van, úgy annak alakja ellipszis, ha eltávolodnak egymástól, akkor a pálya parabola vagy hiperbola alakú. (Kéttest-probléma.)
Az optikában a tükrös távcső vagy a fényszóró tükre forgási paraboloid, vagyis olyan felület, mely úgy származtatható, hogy egy parabolát tengelye körül megforgatunk.
Források[szerkesztés]
- Dr. Pattantyús A. Géza: Pattantyús Gépész- és Villamosmérnökök Kézikönyve 1. kötet. Műszaki Könyvkiadó, Budapest, 1961.
- J. N. Bronstein - K. A. Szemengyajev: Matematikai zsebkönyv. Műszaki könyvkiadó, Budapest, 1987. ISBN 963-10-5309-1
- ELTE Matematikai Intézet[halott link]












































