Euklideszi algoritmus

Az euklideszi algoritmus[1] egy számelméleti algoritmus, amellyel két szám legnagyobb közös osztója határozható meg. Nevét az ókori görög matematikusról, Eukleidészről kapta, aki az Elemekben írta le (Kr. e. 300 körül). Az egyik legrégibb, gyakran használt algoritmus.
Alapötlete az, hogy a legnagyobb közös osztó nem változik, ha a nagyobb számot a két szám különbségével helyettesítjük. Például 252 és 105 legnagyobb közös osztója 21, amely legnagyobb közös osztója a 105 és a 147 = 252 − 105 számoknak is. Ez a helyettesítés csökkenti a nagyobb számot, így a cserék ismétlésével egyre kisebb számokat kapunk, egészen addig, amíg a két szám egyenlővé nem válik. Ez az eddigi számpárok, így az eredeti számpár legnagyobb közös osztója. Az algoritmus lépésein visszafelé menve találunk két egész (akár negatív) tényezőt, amelyek felhasználásával a legnagyobb közös osztó kifejezhető a két kiindulási szám lineáris kombinációjaként.
Ha feltesszük, hogy a kivonások és a maradékos osztások ideje körülbelül megegyezik, akkor az algoritmusnak van egy gyorsabb változata is, amely a kivonások helyett maradékos osztással működik. Ennek lényege, hogy ha a nagyobb szám sokkal nagyobb, mint a kisebb, akkor sok kivonást kell elvégezni addig, amíg a két szám szerepe felcserélődik. A maradékképzés művelete ezt a sok kivonást egy lépésben végzi el. Az algoritmus akkor ér véget, amikor a maradék nulla lesz. Ekkor a legnagyobb közös osztó éppen a kisebb szám. Ezzel az algoritmus lépésszáma a kisebb szám logaritmusával arányossá válik (sohasem nagyobb, mint a tízes számrendszerbeli jegyek számának ötszöröse). A 20. század folyamán további optimalizációt végeztek.
Az algoritmusnak számos alkalmazása van. A törtek egyszerűsítése mellett a moduláris aritmetika osztás műveletének megvalósításában is szerepel. Ehhez az ax ≡ c mod b kongruenciát kell megoldani, ezt a Lineáris diofantoszi egyenletek szakasz írja le részletesebben. Használható diofantoszi egyenletek megoldására, mint amilyen például a kínai maradéktételben szereplő szimultán kongruenciarendszer. Alkalmas lánctörtbe fejtéshez és irracionális számok közelítéséhez. Végül, de nem utolsósorban számelméleti tételek bizonyításának is hasznos segédeszköze; felhasználja a négynégyzetszám-tétel és a számelmélet alaptétele.
Eredetileg egész számokra és szakaszokra használták, de a 19. században általánosították Gauss-egészekre és egyváltozós polinomokra.
Háttere[szerkesztés]

Az algoritmus alapesetben természetes számok legnagyobb közös osztóját számítja ki, amely a legnagyobb olyan természetes szám, amely mindkettőnek osztója. Az a és b számok legnagyobb közös osztójának jelölése lnko(a, b) vagy egyszerűbben (a, b),[2] – habár ez utóbbival más matematikai objektumokat is szoktak jelölni, például vektorokat.
Ha lnko(a, b) = 1, akkor a két szám relatív prím.[3] Ebből nem következik, hogy a két szám prím,[4] vagy egyikük prím, habár két különböző prímszám relatív prím. Az egy minden egészhez relatív prím, de például 35 és 6 is relatív prímek: 6 = 2 × 3 és 35 = 5 × 7. Mivel nincsenek közös prímtényezőik, csak az egy osztója mindkét számnak.
Legyen g = lnko(a, b). Mivel a és b többszöröse g-nek, azért ezek felírhatók, mint a = mg, és b = ng. Az m és az n számok relatív prímek, különben ki lehetne emelni belőlük a legnagyobb közös osztót, így kiderülne, hogy az a és b számoknak van g-nél nagyobb közös osztójuk, tehát g nem legnagyobb közös osztó. A legnagyobb közös osztó a közös osztók többszöröse.[5]
A legnagyobb közös osztó megjeleníthető a következőképpen: [6]
Legyenek egy téglalap oldalai a és b hosszúak. Ekkor a téglalap felosztható c oldalhosszú négyzetrácsra, ha c közös osztója a-nak és b-nek. A legnagyobb közös osztó a lehető legnagyobb szám, amelyre ez lehetséges. Például a 24-szer 60-as téglalap felosztható a következő méretű négyzetekre: 1, 2, 3, 4, 6 és 12 oldalhosszúakra, amelyek közül a legnagyobb a 12. Ekkor az egyik oldal irányában 2, a másik irányában 5 négyzet van.
A legnagyobb közös osztó a prímtényezős felbontásból is megállapítható, mert a közös prímtényezők összeszorzásával állítható elő, ahol is a kitevő a két szám kanonikus alakjában szereplő minimális kitevő.[7] Például 1386 = 2 × 3 × 3 × 7 × 11, és 3213 = 3 × 3 × 3 × 7 × 17, legnagyobb közös osztójuk 63 = 3 × 3 × 7. Ha a számoknak nincsenek közös prímtényezőik, akkor relatív prímek, legnagyobb közös osztójuk 1. A prímtényezős felbontás megtalálása nehéz, amit a kriptográfia ki is használ.[8] Az euklideszi algoritmusnak az az előnye, hogy enélkül képes meghatározni a legnagyobb közös osztót.[9][10]
A legnagyobb közös osztó egy másik definíciója a felsőbb matematikában, közelebbről a gyűrűelméletben hasznos.[11] Két, nullától különböző egész szám legnagyobb közös osztója a legkisebb, egész együtthatókkal előállítható lineáris kombinációjuk; azaz, a és b legnagyobb közös osztója felírható, mint ua + vb, ahol u és v akár negatív egészek. Ez a Bézout-lemma. Az összes lineáris kombináció a legnagyobb közös osztó többszöröse. Ezek a legnagyobb közös osztó által generált főideál elemei, amely így megegyezik az a és a b által generált ideállal. Következik, hogy az egészek minden ideálja főideál. Egyes tulajdonságok könnyebben láthatók ezzel, például hogy a és b minden közös osztója g-nek is osztója, hiszen ua + vb mindkét tagjának osztója.
Három vagy több szám legnagyobb közös osztója a prímtényezős felbontásból is megállapítható, mert a közös prímtényezők összeszorzásával állítható elő, ahol is a kitevő a számok kanonikus alakjában szereplő minimális kitevő.[12] Kiszámítható úgy is, hogy először vesszük két szám legnagyobb közös osztóját, majd ezt a két számot a legnagyobb közös osztójukkal helyettesítve ezt addig ismételjük, amíg egyetlen szám nem marad.[13] A legnagyobb közös osztó szimmetrikus és asszociatív.
- lnko(a, b, c) = lnko(a, lnko(b, c)) = lnko(lnko(a, b), c) = lnko(lnko(a, c), b).
Emiatt az euklideszi algoritmussal nemcsak két, hanem akárhány, de véges sok szám legnagyobb közös osztója is kiszámítható.
Formális leírása[szerkesztés]
Az euklideszi algoritmus egymást követő lépései az előző lépés eredményéből indulnak ki. A lépéseket a k index számolja nullától kezdődően. Így a kezdőlépés a k = 0, a következő lépés a k = 1 indexet használja, és így tovább.
Minden lépés az rk−1 és rk−2 maradékokat használja. Mivel a maradékok folyamatosan csökkennek, azért rk−1 kisebb, mint rk−2. A cél az, hogy találjunk egy qk hányadost és egy rk maradékot, amellyel az
egyenlőség teljesül. Szavakkal, a nagyobb rk−2 számból a kisebb rk−1 többszöröseit vonja le, amíg egy még kisebb rk számhoz nem jut.
A (k = 0) kezdőlépésben az r−2 és r−1 számok megfeleltethetők a kiindulási számoknak. A következő lépésben (k = 1) a kisebb kezdőszám és a nulladik lépésben kapott r0 maradékot használja, és így tovább. Így az algoritmus írható mint az
egyenlőségek sorozata.
Ha a kisebb szám az a, akkor az első lépésben az algoritmus felcseréli a számokat. Például, ha a < b, akkor az első q0 hányados nulla lesz, és a maradék r0 = a. Ettől kezdve az rk maradék mindig kisebb lesz, mint az előző rk−1 maradék minden k ≥ 0 indexre. Mivel a maradékok minden lépésben csökkennek, és sosem lehetnek negatívok, így előbb-utóbb lesz egy maradék, rN = 0[14] Az utolsó nem nulla maradék lesz a legnagyobb közös osztó. Az N nem lehet végtelen, mert csak véges sok egész van a nulla és az első r0 maradék között.
Bizonyítás[szerkesztés]
Az algoritmus érvényessége két lépésben bizonyítható.[15]
Első lépésként lássuk be, hogy az algoritmus véges sok lépés után véget ér. Ennek főleg gyakorlati szempontok miatt van szerepe. Mivel az euklideszi osztás során a maradék kisebb, mint az osztó abszolút értéke, a maradékok szigorúan monoton csökkenő sorozatot alkotnak a természetes számok halmazában, így a sorozat utolsó tagja biztosan nulla, mivel két különböző természetes szám különbsége nem lehet kisebb 1-nél (természetesen az abszolút értékét tekintve):
A következő lépés, hogy bebizonyítjuk: az utolsó maradék közös osztó. Ehhez alulról felfelé haladunk az eljárásban:
Mivel osztója -nek és -nek is, ezért a lineáris kombinációjuknak is. Az eljárást végigkövetve kapjuk, hogy és .[16][17]
Végül bizonyítjuk a maximalitást. Ennek során kihasználjuk azt a tényt, hogy a közös osztók egy szigorúan monoton növekvő természetes számsort alkotnak, amelynek felső határa , valamint hogy a lánc minden tagja osztója az utána következőnek. Tegyük fel, hogy a legnagyobb közös osztó . Ekkor, mivel is közös osztó, . Viszont, mivel a közös osztók osztói a két szám lineáris kombinációinak is, így a lánc elemeire felírva kapjuk:
- .
- .
Mivel a feltételünk az volt, hogy osztója -nek, ezért az oszthatóság definíciója miatt . QED
Példa[szerkesztés]

A 360 és a 225 legnagyobb közös osztójának meghatározása az euklideszi algoritmussal:
Tehát a legnagyobb közös osztó a 45.
Az a = 1071 és b = 462. Először 1071-ből levonogatjuk 462-t, amíg annál kisebb számot nem kapunk. Kétszer kell levonnunk, és marad 147:
- 1071 = 2 × 462 + 147.
Most 462-ből vonogatjuk ki 147 többszöröseit, és marad 21:
- 462 = 3 × 147 + 21.
Ezután 21-et vonogatunk le 147-ből, és a maradék 0 lesz:
- 147 = 7 × 21 + 0.
Mivel az utolsó maradék nulla, azért az algoritmus szerint a legnagyobb közös osztó a 21. Ez megegyezik azzal, amit prímtényezős felbontással találhatunk. Táblázattal:
| k | Egyenlet | Hányados és maradék |
|---|---|---|
| 0 | 1071 = q0 462 + r0 | q0 = 2 és r0 = 147 |
| 1 | 462 = q1 147 + r1 | q1 = 3 és r1 = 21 |
| 2 | 147 = q2 21 + r2 | q2 = 7 és r2 = 0; az algoritmus befejeződik |
Megjelenítése[szerkesztés]
Az algoritmus megjeleníthető a legnagyobb közös osztó fent részletezett tulajdonsága alapján.[18] Az a × b méretű téglalapot megpróbáljuk lefedni a kisebb számnak megfelelő méretű négyzetekkel, amelyből a kisebb szám × r0 méretű téglalap marad. Ezután ezt r0 méretű négyzetekkel, majd a kimaradt területet r1 méretű négyzetekkel próbáljuk lefedni, és így tovább. Ha az összes területet lefedte, akkor az algoritmus véget ér, és a legkisebb méretű négyzet mérete lesz a legnagyobb közös osztó.
Az osztásos módszer[szerkesztés]
Az osztásos módszerben a maradékos osztás definíciója alapján vannak olyan számok, hogy rk−2 = qk rk−1 + rk, ahol a maradék szigorúan kisebb, mint az osztó. A maradék és a hányados egyértelmű.[19]
Az osztásos módszer csökkenti a lépések számát. Ha nem akarjuk kifejezni a legnagyobb közös osztót lineáris kombinációként, akkor nincs szükség a hányadosokra. Ezzel egy lépés alakja: rk = rk−2 mod rk−1.
Az abszolút értékben legkisebb maradék módszere[szerkesztés]
Ebben a módszerben az algoritmus minden lépésben eggyel növeli a hányadost, ha a negatív maradék abszolút értéke kisebb, mint a pozitív maradék.[20][21] Az általános algoritmus felteszi, hogy az
- rk−2 = qk rk−1 + rk
egyenletben |rk−1| > rk > 0. Ezzel szemben kiszámítható egy negatív maradék is:
- rk−2 = (qk + 1) rk−1 + ek
ha rk−1 > 0, vagy
- =rk−2 = (qk − 1) rk−1 + ek,
ha rk−1 < 0.
Ha rk helyett az algoritmus ek-t veszi, ha |ek| < |rk|, akkor teljesülni fog, hogy: |rk| ≤ |rk−1| / 2
Leopold Kronecker belátta, hogy az összes változat közül ennek a lépésszáma a legkisebb,[22][21] minden a, b kiinduló számpárra akkor és csak akkor minimális a lépésszám, ha qk-t úgy választja, hogy , ahol az aranymetszés.[23]
Bonyolultsága[szerkesztés]

- Az algoritmus a leggyorsabban akkor ér véget, ha .
- Az algoritmus a szomszédos Fibonacci-számok esetén rendkívül lassú, ennek oka, hogy végigfut visszafelé a teljes sorozaton. A sorozat ugyanis szigorúan monoton növekvő, valamint a definíció szerint
- ami megfelel a maradékos osztás definíciójának. Ez Émile Léger eredménye (1837).[24]
- Szakaszok esetén is értelmezhető a maradékos osztás, így az euklideszi algoritmus is elvégezhető. Itt azonban nem tudjuk biztosítani az eljárás véges hosszát. Ha ez teljesül, akkor a két szakasz összemérhető.
Az algoritmus bonyolultságát alaposan áttanulmányozták[25] Az algoritmusok bonyolultságát a megtett lépések számával mérik. Mivel az egyes lépések végrehajtási ideje különböző, ezért számításba veszik, hogy például az osztás mennyivel lassabb a kivonásnál. Valójában többnyire csak a nagyságrend érdekes, mert lényeges, hogy a számítási kapacitás növelésével mennyivel nagyobb feladat oldható meg az adott algoritmussal.
Az euklideszi algoritmus bonyolultságát először A.-A.-L. Reynaud elemezte. 1811-ben megmutatta, hogy a lépések számának felső korlátja a kisebb bemenő szám. Ha a számok a, b, és b < a, akkor a korlát b. Később jobb becslést is adott: b/2 + 2.,[26] P.-J.-E. Finck 1841-ben megmutatta, hogy az osztások száma legfeljebb ,[27] így az algoritmus polinomiális a bemenet méretében.[24] Ezt 1844-ben Gabriel Lamé finomította azzal,[28] hogy a lépések száma soha nem nagyobb, mint a kisebb szám tízes számrendszerbeli jegyeinek számának ötszöröse.[29][30]
Az egységes költség modellben Lamé eredménye szerint a költség O(h); ám ha a számok nagyok, akkor nem hanyagolható el, hogy a maradékképzés drágább, mint az osztás, így az algoritmus költsége egy nagyságrendet nő, O(h2) lesz.[31] Ekkor a lépésszámra egy teleszkopikus összeget kaphatunk, amely szintén ezt a becslést adja. A modern gyors egészszorzásos Schönhage–Strassen algoritmussal felgyorsítható, így az algoritmus kvázilineáris lehet.[32][33]
A lépések száma[szerkesztés]
Két természetes szám, a és b legnagyobb közös osztójának kiszámításához szükséges lépések számát T(a, b) jelöli.[34] Ha a és b legnagyobb közös osztója g, akkor a = mg, b = ng, és az n és m természetes számok relatív prímek. Ekkor
- T(a, b) = T(m, n)
ami belátható, ha az algoritmusban mindenütt végigosztunk g-vel.[35] Hasonló teljesül, ha végigszorzunk egy közös tényezővel:
- w: T(a, b) = T(wa, wb).
Így a T lépésszám erősen hullámzik a szomszédos számpárok között, a legnagyobb közös osztó méretétől függően.
Az euklideszi algoritmus rekurzív természete miatt
- T(a, b) = 1 + T(b, r0) = 2 + T(r0, r1) = … = N + T(rN−2, rN−1) = N + 1
ahonnan T(x, 0) = 0.[36]
A legrosszabb eset[szerkesztés]
Ha az algoritmus egy a > b > 0 számpárra N lépést tesz meg, akkor a legkisebb ilyen számpár a Fibonacci-sorozat két szomszédos tagja, FN+2 és FN+1.[37] Ez teljes indukcióval látható be.[38] Ha N = 1, akkor b osztója a-nak.[39] A legkisebb ilyen pozitív számpár b = 1 és a = 2, amelyek rendre megegyeznek F2-vel és F3-mal.
Most tegyük fel, hogy az állítás már be van bizonyítva minden N-re egészen M − 1-ig. Az első lépés a = q0b + r0, és a második b = q1r0 + r1. Az algoritmus rekurzív természete miatt M − 1 lépés kell lnko(b, r0) megtalálásához, és legkisebb értékük FM+1 és FM. Emiatt a legkisebb lehetséges értéke q0 = 1, innen a = b + r0 = FM+1 + FM = FM+2. Ezt a bizonyítást Gabriel Lamé adta 1844-ben, ami a bonyolultságelmélet kezdetét jelenti,[40] továbbá az első példa a Fibonacci-számok gyakorlati felhasználására.[41]
Az eredményből az is következik, hogy a lépések száma nem haladhatja meg a kisebb szám tízes számrendszerbeli számjegyeinek számának ötszörösét.[42] Ha az algoritmus N lépést tesz meg, akkor b legalább FN+1, amelynek alsó becslése φN−1, ahol φ az aranymetszés. Mivel b ≥ φN−1, azért N − 1 ≤ logφb. Mivelhogy log10φ > 1/5, (N − 1)/5 < log10φ logφb = log10b. Ezért N ≤ 5 log10b. Tehát az euklideszi algoritmus mindig legfeljebb O(h) osztást igényel, ahol h a kisebb szám jegyeinek száma.
Átlagos lépésszám[szerkesztés]
Az átlagos lépésszám többféleképpen is definiálható. Az egyik definíció szerint a T(a) átlagos időt úgy mérjük, hogy az a számhoz a nála kisebb pozitív egészekkel vett legnagyobb közös osztó kiszámításához szükséges időket átlagoljuk.[43]
Azonban, mivel T(a, b) erősen változik a legnagyobb közös osztóval együtt, a T(a) függvény is ennek megfelelően zajos.[44] Emiatt vezették be azt az átlagot, amely csak a relatív prímekkel számol:
Az a-nál kisebb relatív prímek száma φ(a), ahol φ az Euler-függvény. Ez már elég jól becsülhető:[45][46]
A hibatag a−(1/6) + ε, ahol ε tetszőlegesen kicsi. A képletben a C (Porter-konstans[47]):
ahol γ az Euler–Mascheroni-konstans és ζ' a Riemann-féle zétafüggvény deriváltja.[48][49] A főegyüttható, (12/π2) ln 2 két, egymástól független módszerrel határozható meg.[50][51]
Az első átlagfüggvény az a szám osztóinak tau átlagával számítható ki:[52]
és a következőképpen approximálható:[53]
ahol Λ(d) a von Mangoldt-függvény.[54]
A harmadik átlag az Y(n), amely a várható lépésszámot adja meg, ha a két számot az 1-től n-ig terjedő számok közül egyenletes valószínűséggel sorsolják.[53]
Behelyettesítve a T(a)-ra vonatkozó approximációt adódik Y(n) approximációja: [55]
Lépésenkénti költség[szerkesztés]
Az algoritmus minden k-adik lépésében a qk hányados és az rk maradékot számítja ki az rk−2 és rk−1 számokból kiindulva:
- rk−2 = qk rk−1 + rk.
A költséget inkább a qk hányados kiszámítása jelenti, mert a maradék gyorsan megkapható:
- rk = rk−2 − qk rk−1.
Két h bites szám osztásának költsége O(h(ℓ+1)), ahol ℓ a hányados hossza.[56]
Az eredeti, kivonásos módszer lassabb lehet. Az osztás eredményét adódó hányados az a szám, ahányszor ki kell vonni a kisebb számot a nagyobból, hogy a számok szerepet cseréljenek. Ha a hányados nagy, akkor sok kivonásra van szükség. Másrészt azonban a hányados általában kicsi marad. Annak a valószínűsége, hogy egy adott q szám hányados, megközelítőleg ln|u/(u − 1)|, ahol u = (q + 1)2.[57] Például annak a valószínűsége, hogy a hányados 1, 2, 3 vagy 4, rendre 41,5%, 17,0%, 9,3% és 5,9%. Azonban a kivonás gyorsabban elvégezhető, mint az osztás, különösen a nagy számok esetén,[58] így a kivonásos módszer versenyképes az osztásossal.[59]
Kombinálva a lépésszámok becslését a lépésenkénti becsült számításigénnyel belátható, hogy az euklideszi algoritmus kvadratikusan nő a jegyek átlagos számában (h2). Reprezentálják h0, :h1, …, hN−1 az r0, r1, …, rN−1 maradékok jegyeinek számát! Mivel a lépések N száma lineárisan nő h-val, a futási idő korlátja:
Alternatív módszerek[szerkesztés]
Egyszerűsége miatt az euklideszi algoritmus széles körben használt, különösen kis számokra.[60] Alternatívái nála sokkal lassabbak lehetnek.
Egy jóval kevésbé hatékony módszer a legnagyobb közös osztó megtalálására a két szám közös osztóinak meghatározása szitálással. Ezek közül a legnagyobb lesz a legnagyobb közös osztó. A szitálás 2-től indul, és a kisebb számig tart. Ez lineárisan nő a kisebb számmal, vagyis exponenciálisan a jegyek számában. Hasonlóan kevéssé hatékony a prímtényezős felbontáson alapuló módszer.[61] A prímtényezős felbontás megtalálását faktorizálásnak nevezik, és kevéssé hatékony, emiatt kriptográfiai módszereket is alapoznak rá.[62]
A bináris legnagyobb közös osztó algoritmus kihasználja, hogy a számítógépek kettes számrendszerben számolnak; így az osztás helyettesíthető gyorsabb műveletekkel.[63][64] Ennek a műveletigénye szintén O(h²). Mindazonáltal a gyorsabb műveletek miatt gyorsabban fut, mint az euklideszi algoritmus, azonban ugyanúgy skálázódik.[65] A hatékonyság tovább javítható, ha a számoknak csak az első jegyét tekintik.[66][67] Az algoritmus más számrendszerekre is kiterjeszthető, amivel a sebesség ötszörösére növelhető.[68] Lehmer legnagyobb közös osztó algoritmusa ugyanezen az elven alapul, de bármely számrendszerben működik.
Nagyon nagy egészekre (egészen 25 ezer jegyig) rekurzív megközelítésekkel kvázilineáris sebesség érhető el.[69] Ezek közé tartoznak Schönhage,[70][71] és Stehlé és Zimmermann módszere.[72] Ezek az euklideszi algoritmus mátrixos alakját használják fel. Sebességük O(h (log h)2 (log log h)).[73][33]
Programkód[szerkesztés]
C-ben[szerkesztés]
#include <stdio.h>
int lnko(int a, int b){
int temp;
while(b>0){
temp = b;
b = a%b;
a = temp;
}
return a;
}
int main(void){
int s1, s2;
printf("szam1 szam2: ");
scanf("%d %d", &s1, &s2);
printf("lnko(%d, %d)=%d", s1, s2, lnko(s1, s2));
return 0;
}
A k-adik iterációban a b változó tartalmazza rk−1-et, míg az a a megelőzőt, rk−2-t. A b = a%b; lépés megfelel a fenti rk ≡ rk−2 mod rk−1 formulának. A temp változó a rk−1 értékét tartalmazza az rk kiszámítása közben. A ciklus végén b tartalmazza rk-t, és a az előző maradékot, rk−1-et.[74]
Java nyelvű példa rekurzióval[szerkesztés]
Rekurzióval megvalósítva Java nyelven:
class GreaterCommonDivider {
public static int gcd(int a, int b) {
if(a%b == 0) {
return b;
} else {
return gcd(b, a%b);
}
}
public static void main(String args[]) {
if(args.length != 2) {
System.exit(1);
}
System.out.println( gcd( Integer.parseInt( args[0] ), Integer.parseInt( args[1] ) ) );
System.exit(0);
}
}
A rekurzió azt használja ki,[75] hogy a maradékképzés során megmarad a legnagyobb közös osztó, és a megállási feltétel lnko(rN−1, 0) = rN−1. Például az lnko(1071, 462) kiszámítható azzal, hogy lnko(462, 1071 mod 462) = lnko(462, 147). Ez ugyanaz, mint lnko(147, 462 mod 147) = lnko(147, 21), azaz lnko(21, 147 mod 21) = lnko(21, 0) = 21.
A kivonásos változatban maradékképzés helyett ismételt kivonás szerepel.[76] Az osztásos módszerrel szemben ez csak pozitív számokra működik, és megáll, ha a = b. Pszeudokódja:
function gcd(a, b)
while a ≠ b
if a > b
a := a − b;
else
b := b − a;
return a;
Az a és b változók felváltva tárolják a maradékokat. Feltéve, hogy az elején az a a nagyobb, a = rk−2, mivel rk−2 > rk−1. Az adott iterációban az a változót az előző maradék többszöröseivel csökkenti, amíg a kisebbé nem válik, mint b. Ekkor a = rk, és a szerepek megcserélődnek, amivel az rk+1 maradékot számolja ki, majd újabb szerepcsere, és így tovább.
Megvalósítása Python programozási nyelven[szerkesztés]
def Lnko(a, b):
if a == b:
return a
if b < a:
a, b = b, a
while (0 < a):
a, b = b % a, a
return b
a = int(input("Adjon meg egy szamot: "))
b = int(input("Adjon meg egy masik szamot: "))
print(Lnko(a, b))
Matematikai alkalmazások[szerkesztés]
Bézout-lemma[szerkesztés]
A Bézout-lemma szerint az a és a b számok legnagyobb közös osztója előállítható, mint g = sa + tb, ahol s és t egész számok.[77] Másképpen szólva mindig lehetséges olyan s és t egészeket találni, hogy g = sa + tb.[78][79]
Az s és a t a q0, q1, … hányadosokból számítható, az algoritmus megfordításával.[80] Elindulva visszafelé, g kifejezhető a qN−1 hányadossal és a két korábbi rN−2 és rN−3 maradékkal:
- g = rN−1 = rN−3 − qN−1 rN−2 .
Ezek a maradékok hasonlóan írhatók fel:
- rN−2 = rN−4 − qN−2 rN−3 és
- rN−3 = rN−5 − qN−3 rN−4 .
Visszahelyettesítve kapjuk a g legnagyobb közös osztót mint rN−4 és rN−5 lineáris kombinációját. Ezt folytatjuk, amíg el nem érünk az első két számhoz:
- r2 = r0 − q2 r1
- r1 = b − q1 r0
- r0 = a − q0 b.
Az összes r0, r1, … maradék helyettesítése után kifejezzük g-t, mint a és b lineáris összegét: g = sa + tb. A Bézout-lemma és az euklideszi algoritmus általánosítható az euklideszi tartományokra (normált, nullosztómentes, nem nullgyűrű).
Főideálok és a hozzájuk kapcsolódó problémák[szerkesztés]
A Bézout-lemma egy újabb definíciót ad a legnagyobb közös osztóra.[81] Tekintsük azokat a számokat, amelyek kifejezhetők ua + vb alakban, ahol u, v egészek. Mivel a és b is osztható g-vel, azért ezek a számok is oszthatók lesznek g-vel. Más szavakkal, a halmaz minden eleme többszöröse g-nek, ami a és b összes közös osztójára igaz, de a g az egyetlen közös osztó, amely eleme ennek a halmaznak, mivel a Bézout-lemma által megadott egészek megfelelnek. Egy kisebb közös osztó nem lehet a halmazban, mivel annak minden eleme osztható kell, hogy legyen g-vel. Továbbá a legnagyobb közös osztó minden többszöröse kifejezhető lineáris kombinációként, u = ms és v = mt választással, ahol s és t a Bézout-lemma által megadott egészek. Ez látható, ha a lemma egyenletét megszorozzuk m-mel:
- mg = msa + mtb.
Ezért az ua + vb alakú számok halmaza megegyezik g többszöröseinek halmazával. Azaz két egész egész együtthatós lineáris kombinációinak halmaza megegyezik legnagyobb közös osztójuk többszöröseinek halmazával. A gyűrűelméletben azt mondják, hogy a legnagyobb közös osztó a két szám által generált ideál generátora. Ez vezetett a főideál és a főideálgyűrű fogalmához.
Ez alapján egy további probléma is megoldható.[82] Az öntögetési feladatokban adva van két edény, a és b űrtartalommal. Egy harmadik, elég nagy térfogatú edényben hozzátöltéssel és elvétellel bármely ua + vb űrtartalom kimérhető. Ezek mind g = lnko(a, b) többszörösei.
Kiterjesztett euklideszi algoritmus[szerkesztés]
A kiterjesztett algoritmus a legnagyobb közös osztó mellett a Bézout-lemmában szereplő együtthatókat is számolja. Ez két rekurzív egyenletet ad az algoritmushoz:[83]
- sk = sk−2 − qksk−1
- tk = tk−2 − qktk−1
ahol a kezdőértékek:
- s−2 = 1, t−2 = 0
- s−1 = 0, t−1 = 1.
A rekurzióval az s = sN és t = tN, ahol N+1 az algoritmus utolsó lépése, amikor rN+1 = 0.
A megközelítés helyessége teljes indukcióval bizonyítható. Feltesszük, hogy az algoritmus helyesen működik a k − 1. lépésig, azaz
- rj = sj a + tj b
minden k-nál kisebb j-re. A k-adik lépésből adódik, hogy
- rk = rk−2 − qkrk−1.
Mivel a rekurziós képlet korrekt rk−2 és rk−1 esetén, ez kifejezhető s és t segítségével:
- rk = (sk−2 a + tk−2 b) − qk(sk−1 a + tk−1 b
Átrendezve kapjuk a rekurziós képletet k-ra: rk = sk a + tk b = (sk−2 − qksk−1) a + (tk−2 − qktk−1) b.
Mátrixmódszer[szerkesztés]
A kiterjesztett algoritmusban szereplő s és t megtalálható az ekvivalens mátrixmódszerrel is.[84]
Az algoritmus egyenletei
- a = q0 b + r0
- b = q1 r0 + r1
- …
- rN−2 = qN rN−1 + 0
írhatók úgy is, hogy egy kétszer kettes mátrixot megszorozzuk a két dimenziós maradékvektorral:
Reprezentáljuk az összes hányadosmátrix szorzatát M-mel:
ezzel az algoritmus a következő alakra egyszerűsödik:
Ahhoz, hogy a g legnagyobb közös osztót kifejezzük, az egyenlet mindkét oldalát meg kell szorozni M inverzével.[84][85] Az M inverze létezik, hiszen determinánsa (−1)N+1, mivel megegyezik a hányadosmátrixok determinánsainak szorzatával, amelyek mindegyike mínusz egy. Ekkor az egyenlet megoldása:
Az első egyenlet szerint
- =g = (−1)N+1 ( m22 a − m12 b),
így s = (−1)N+1m22 és t = (−1)Nm12. Hatékonysága megegyezik a rekurzív algoritmusformáéval.
Eukleidész lemmája és az egyértelmű prímtényezős felbontás[szerkesztés]
A Bézout-egyenlőség lényeges szerepet kap az euklideszi algoritmus több alkalmazásában, például az egyértelmű prímtényezőkre bontásban.[86] Ennek bemutatására: Legyen az L szám két tényező szorzata, L = uv. Ekkor, ha L osztható egy w számmal, és ez relatív prím u-hoz, akkor osztója v-nek. Ez a következő gondolatmenettel belátható: Ha u és w relatív prímek, akkor van s és t, hogy
- 1 = su + tw
a Bézout-egyenlőség miatt. Az egyenletet v-vel szorozva:
- v = suv + twv = sL + twv
Mivel w a jobb oldal minden tagjának osztója, azért osztója kell, hogy legyen a bal oldalnak.[87]
Speciálisan, ha egy prímszám osztója L-nek, akkor L valamelyik tényezőjének is osztója kell, hogy legyen. Egy másik megfordítás szerint, ha a1, a2, …, an relatív prímek w-hez, akkor szorzatuk is relatív prím w-hez.[88]
Mindezekkel már könnyen belátható a prímtényezős felbontás egyértelműsége.[89] Tegyük fel indirekt, hogy az L egész számnak két lényegileg különböző prímtényezős felbontásában m, illetve n tényező szerepel, azaz
- L = p1p2…pm = q1q2…qn .
Mivel minden p osztója L-nek, azért legalább egy q-nak osztójának kell lennie; de mivel prím, ezért lényegében meg kell vele egyeznie. Minden p-t és q-t megvizsgálva mindegyik prímnek megtaláljuk a másik oldalon a lényegi megfelelőjét. Ez ellentmondás, így lényegében egyértelmű a felbontás, eltekintve a prímek sorrendjétől és előjelétől.
Lineáris diofantoszi egyenletek[szerkesztés]

A diofantoszi egyenletek azok, amelyek megoldásaként csak egész számok fogadhatók el. A név a Kr. e. 3. századi Diofantoszra utal.[90] A lineáris két ismeretlenes alakja
- ax + by = c
A diofantoszi egyenletben a, b, c, x és y egész számok, és a, b és c adottak.[91] Moduláris aritmetikával:
- ax ≡ c mod b.
Legyen g az a és a b legnagyobb közös osztója. Ekkor ax + by mindkét tagja osztható g-vel, így az egyenlet csak akkor oldható meg, ha c is osztható g-vel. Ekkor mindkét oldalt leosztva c/g-vel visszajutunk a Bezout-egyenlethez:
- sa + tb = g
ahol s és t a kiterjesztett euklideszi algoritmussal található meg.[92] Innen kapunk egy megoldást: x1 = s (c/g) és y1 = t (c/g).
Egy lineáris diofantoszi egyenletnek vagy nincs megoldása, vagy végtelen sok megoldása van.[93] Ennek belátására legyen két megoldás az (x1, y1) és az (x2, y2), ahol
- ax1 + by1 = c = ax2 + by2
vagy ekvivalenesen
- a(x1 − x2) = b(y2 − y1).
Emiatt a két x közötti legkisebb különbség b/g, és az y megoldások közötti legkisebb különbség a/g. Ezzel a megoldások:
- x = x1 − bu/g
- y = y1 + au/g
Ha megengedett, hogy u befussa az egészeket, akkor egy megoldásból végtelen sok nyerhető.
Ha a megoldásokat a pozitív egészekre korlátozzuk, akkor ez véges megoldásszámot ad. Ezzel a korláttal a lineáris diofantoszi egyenletrendszerek még alulhatározva is véges számú megoldást adnak.[94] Ez különbözik attól az esettől, amikor a megengedett megoldások nemcsak egészek lehetnek.
Kínai maradéktétel[szerkesztés]
Az euklideszi algoritmus használatával lineáris diofantoszi egyenletrendszerek oldhatók meg.[95] A kínai maradéktétel éppen ilyen egyenletrendszerekkel foglalkozik. Ha a szám egy megadott határnál kisebb, akkor ábrázolható a jegyei helyett relatív prím modulusokkal vett maradékaival:
ahol mi-k[96] az egyes modulusok, és xi a hozzájuk tartozó maradékok.
Az egyenletrendszer megoldásához ki kell számítani az x egész számot, illetve maradékosztályt modulo M, ahol M a modulusok szorzata. Legyen most Mi a következő:
Ekkor minden Mi a modulusok szorzata, kivéve az mi modulust. A megoldás azon múlik, hogy találjunk hi számokat, hogy
Ezekkel a hi számokkal minden, M-nél kisebb egész x rekonstruálható maradékaiból az
egyenlet alapján. Definíciójuk szerint a hi számok az Mi inverzei, amelyek kiszámíthatók az euklideszi algoritmussal.
Stern–Brocot-fa[szerkesztés]
Az euklideszi algoritmussal a pozitív racionális számok halmaza végtelen bináris keresőfába rendezhető; ezt Stern–Brocot-fának nevezik. A gyökérnél helyezkedik el az 1, a többi szám helye a számláló és a nevező legnagyobb közös osztójának kiszámításával határozható meg az euklideszi algoritmus eredeti formája szerint. Ha a két szám közül az elsőt kell helyettesíteni, akkor jobbra kell lépni, ha a másodikat, akkor balra. Ha az algoritmusnak vége, akkor a számot helyben találjuk.[97] A lépések nem függnek attól, hogy a szám milyen alakban van. Ez arra használható, hogy belássuk, a pozitív racionális számok egyszer jelennek meg a fában.
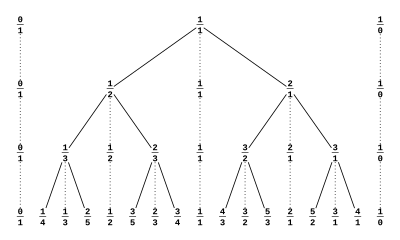
Például a 3/4 eléréséhez egyet balra, majd kettőt jobbra kell lépni:
Az euklideszi algoritmusnak hasonló a kapcsolata a Calkin–Wilf-fával, de ott az irány fordított: a számtól elindulva kell eljutni az egyhez.
Lánctörtek[szerkesztés]
Az euklideszi algoritmus kapcsolatba hozható a lánctörtekkel.[98] Az egyenletek írhatók úgy is, mint
Megfigyelhető, hogy a jobb oldal utolsó tagja a bal oldal inverze. Így az első két egyenlet írható úgy is, mint
A harmadik egyenletben behelyettesítve az r1/r0 hányadossal:
Az rk/rk−1 végső arány helyettesíthető a következő egyenlet szerint, egészen az utolsó egyenletig. A végeredmény egy lánctört:
A fenti példában, amelyben kiszámítottuk az lnko(1071, 462) legnagyobb közös osztót, a hányadosok rendre 2, 3 és 7 voltak. Így az 1071/462 lánctört alakja:
amiről ellenőrző számolással is meggyőződhetünk.
Faktorizáció[szerkesztés]
A legnagyobb közös osztó kiszámítása több faktorizáló algoritmus lényegi eleme,[99] így tartalmazza Pollard rhó algoritmusa,[100] Shor algoritmusa,[101] Dixon faktorizációs módszere[102] és a Lenstra elliptikus görbe faktorizáció.[103] Ezekben az euklideszi algoritmus a legnagyobb közös osztó megtalálására szolgál. A lánctört-faktorizáció lánctörteket használ, amelyek az euklideszi algoritmussal számíthatók ki.[104]
Általánosításai[szerkesztés]
Habár az algoritmus eredeti alakjában a természetes számok legnagyobb közös osztóját számítja ki, általánosítható több különböző matematikai objektumra is, mint racionális számok, polinomok,[105] kvadratikus egészek,[106] és Hurwitz-kvaterniók.[107]Az utóbbi esetben az euklideszi algoritmussal bizonyítható az egyértelmű faktorizáció, amely prím elemek helyett felbonthatatlanok szorzatára való lényegében egyértelmű felbontást jelenti.
Racionális számok[szerkesztés]
Euklidesz valós (nem feltétlenül racionális) számokra terjesztette ki az algoritmust, és azt vizsgálta, hogy található-e két adott (a és b) valós számhoz olyan g valós szám, hogy a és b felírhatók g egész többszöröseként. Ha az egyik szám a, a másik b, akkor van m és n egész szám, amellyel a = mg és b = ng.[108] Ezek ugyanúgy találhatók meg, mint az egészeknél az s és a t együtthatók, amelyekkel sa + tb = 0. Eukleidész ezt az algoritmust használta a nem összemérhető szakaszok tanulmányozására.[109][110]
A racionális számok euklideszi algoritmusa abban különbözik az egészektől, hogy a maradék lehet tört, de a hányadosnak egésznek kell lennie. Ha mindkét szám racionális, akkor az algoritmus előbb-utóbb véget ér, hiszen a közös mértékegység létezik, ami közös nevezőre hozással belátható. Valós számokra rátérve ha azonban egyik, vagy mindkettő irracionális, akkor az algoritmus nem ér véget, ez végtelen lánctörtként írható le. A maradékokat itt is rk jelöli, a hányadosok qk-k. Az a/b = mg/ng = m/n tört lánctört alakja: [q0; q1, q2, …, qN]. Ha az a/b arány irracionális, akkor végtelen lánctörtet kapunk, amelynek lánctört alakja [q0; q1, q2, …].[111] Például az aranymetszés arányszáma φ = [1; 1, 1, …], és a 2 négyzetgyöke [1; 2, 2, …].[112]
Valós számokon az algoritmus leállása nulla valószínűségű, ugyanis majdnem minden valós szám irracionális..[113] A lánctörtek kezdeti szakaszai (k lépés után [q0; q1, q2, …, qk]) közelítést adnak az irracionális számokra, ami hosszabb kezdeti szakasszal javítható. A közelítés egyszerű tört alakra hozva éppen mk/nk, amelyek konvergens sorozatot alkotnak. A számláló és a nevező relatív prím, és a következő rekurzív szabály érvényes rájuk:
- mk = qk mk−1 + mk−2 és
- nk = qk nk−1 + nk−2
ahol m−1 = n−2 = 1 és m−2 = n−1 = 0 a rekurzió kezdőértékei. Az mk/nk konvergens sorozat a legjobb racionális számokból álló közelítő sorozat az a/b-hez az nk nevezővel:[114]
Polinomok[szerkesztés]
Az egy változós polinomok adott gyűrű fölött gyűrűt alkotnak. A gyűrű lehet például az egész számok, a racionális vagy a valós számok. Az ezek fölötti polinomok azok, amelyeknek együtthatói az adott számkörből valók, így az egész, a racionális és a valós együtthatós polinomok összeadhatók, kivonhatók és szorozhatók, és az eredmény polinomok együtthatói is a megfelelő számkörből valók. Definiálható a maradékos osztás is. A következőkben testek fölötti polinomokról lesz szó, vagyis az együtthatókat még osztani is lehet.
A polinomok körében a prímszámok megfelelői a felbonthatatlanok, más néven irreducibilis polinomok. Két polinom, a(x) és b(x) legnagyobb közös osztója az egész számokhoz hasonlóan definiálható az irreducibilis felbontásuk segítségével, és meghatározható az euklideszi algoritmussal.[105]
Az eljárás hasonlít az egészekéhez. A k-adik lépésben a qk(x) hányados és az rk(x) maradék polinom eleget tesz az
- rk−2(x) = qk(x) rk−1(x) + rk(x)
rekurzív egyenletnek, ahol r−2(x) = a(x) és r−1(x) = b(x). A hányados polinom qk(x) rk−1 együtthatóját úgy választják, hogy megegyezzen rk−2(x) legmagasabb fokú tagjával; ez biztosítja, hogy a maradékok foka csökkenjen. Ezzel belátható, hogy az euklideszi algoritmus véget ér. Az utolsó nem nulla maradék lesz a polinomok legnagyobb közös osztója.[115]
Például vegyük a következő, másodfokú polinomok szorzatára bomló polinomokat:
- a(x) = x4 − 4x3 + 4 x2 − 3x + 14 = (x2 − 5x + 7)(x2 + x + 2 és
- b(x) = x4 + 8x3 + 12x2 + 17x + 6 = (x2 + 7x + 3)(x2 + x + 2).
Az első maradék az a(x) / b(x) osztást elvégezve r0(x) = x3 + (2/3) x2 + (5/3) x − (2/3). A következő lépésben b(x)-et osztjuk r0(x)-szel, és maradékként r1(x) = x2 + x + 2 adódik. Végül az r0(x) osztás r1(x)-szel nullát ad maradékul, így az algoritmus véget ér.
Több alkalmazás is átvihető az egészekről a polinomokra,[116] így megoldhatók vele lineáris diofantoszi egyenletrendszerek a polinomokra, és szimultán lineáris kongruenciarendszerek is. A polinomokra is definiálhatók lánctörtek, és a lánctörtbe fejtés is elvégezhető. De vannak más alkalmazások is, például a Sturm-láncok egy adott intervallumban keresik a polinom gyökeit.[117] Ennek további felhasználási területei vannak a vezérléselméletben a Routh–Hurwitz stabilitási kritérium.[118]
A fentiek akkor is alkalmazhatók, ha az együtthatók a véges testek elemei, vagy lehetnek más, általánosabb testből.[105]
Gauss-egészek[szerkesztés]
A Gauss-egészek α = u + vi alakú komplex számok, ahol u és v valós egészek, és i a képzetes egység.[119]Az euklideszi algoritmus bevezetésével megmutatható, hogy egyértelműen bomlanak fel, ahogy azt a fenti Bézout-egyenlőség is mutatja.[120] Ezt aztán több alkalmazásban is felhasználják, mint a pitagoraszi számhármasok előállítása.[121] A tételek gyakran máshogy is bizonyíthatók, az euklideszi algoritmus kényelmi eszköz.
A Gauss-egészekre használt euklideszi algoritmus majdnem ugyanaz, mint a valós egészekre használt.[122] Itt a qk hányadost és az rk maradékot úgy választják, hogy
- rk = rk−2 − qk rk−1,
ahol α, β kiindulási Gauss-egészek, és rk−2 = α, rk−1 = β. A maradékok nagyságának csökkenését a komplex abszolút értékben mérik, tehát |rk| < |rk−1| valós nem negatív egészek, ami ahhoz kell, hogy bizonyítható legyen az algoritmus végessége.[123] A maradékok és a hányadosok Gauss-egészek. A qk maradékokat általában úgy számolják, hogy az α/β pontos arány valós és képzetes részét egészekre kerekítik.[122] Az utolsó nem nulla maradék lnko(α,β), a legnagyobb abszolút értékű Gauss-egész, amely mindkét kiindulási számnak osztója. Ez lényegében egyértelmű, azaz egységgel szorzás erejéig egyértelmű. Az egységek ±1 és ±i.[124]
Több alkalmazás is átvihető Gauss-egészekre, például a lineáris diofantoszi egyenletek és a szimultán kongruenciarendszerek megoldása.[125] A lánctörtbe fejtés is elvégezhető.[122]
Euklideszi gyűrűk[szerkesztés]
Az euklideszi gyűrűk kommutatív gyűrűk, amelyekben euklideszi norma biztosítja, hogy elvégezhető az euklideszi algoritmus.[126][127] Ez egy f leképezés a gyűrű elemein, amely az összes elemet a nem negatív egész számokra képezi le. Teljesíti továbbá azt is, hogy ha a és b a gyűrű nullától különböző elemei, akkor van olyan q és r elem, hogy a = qb + r és f(r) < f(b).[128] Ilyen norma a polinomoknál a fok[129] és a Gauss-egészeknél az abszolút érték négyzete.[130]
A számelmélet alaptétele minden euklideszi gyűrűben bizonyítható. Ez azt jelenti, hogy minden nullától különböző elem lényegében egyértelműen felbontható irreducibilis elemek szorzatára. Ezzel a tulajdonsággal az euklideszi gyűrűk egyértelmű faktorizációs gyűrűk. Megfordítva azonban nem minden egyértelmű faktorizációs gyűrű euklideszi.[131] Az egyértelmű faktorizációs gyűrűkben létezik a legnagyobb közös osztó, bár ez nem mindig található meg euklideszi algoritmussal.[132] Az euklideszi gyűrűk főideáltartományok[forrás?], azaz integritási tartományok, ahol minden ideál főideál. A főideálgyűrűk azonban nem biztos, hogy euklideszi gyűrűk.[133]
Az euklideszi gyűrűkben az egyértelmű irreducibilis felbontás több alkalmazásban is hasznos. Például a Gauss-egészekkel kényelmesen megadhatók a pitagoraszi számhármasok.[134] Ezen felbuzdulva Gabriel Lamé hasonlóval próbálkozott 1847-ben, amikor a nagy Fermat-tételt próbálta bizonyítani. Joseph Liouville javaslatával foglalkozott az euklideszi algoritmus hatékonyságával is.[135] Bizonyítása azon a feltevésen alapult, hogy az x + ωy alakú számok egyértelműen faktorizálhatók, ahol x, y egészek, és ω = e2iπ/n n-edik komplex egységgyök, azaz ωn = 1. Az alapfeltevés azonban nem igaz minden n-re, így Ernst Kummer az ideális számok bevezetésével próbálta javítani a hibát, ami alapján Richard Dedekind megalapozta az ideálok fogalmát.[136]
Kvadratikus egészek[szerkesztés]
A kvadratikus testek egészgyűrűi segítenek bemutatni az euklideszi gyűrűket.
A kvadratikus testek a racionális számtest alakú másodfokú bővítései, ahol D négyzetmentes egész szám.
Egy adott kvadratikus test egészgyűrűjének elemeit kvadratikus egészeknek nevezzük. Adott D-re a kvadratikus egészek tehát az algebrai egészek gyűrűjének részgyűrűjét alkotják. Az egészgyűrű elemeit D = −1 esetben Gauss-egészeknek, D = −3 esetben Eisenstein-egészeknek nevezzük. Minden kvadratikus egész felírható alakban, ahol u és v egész vagy félegész. (Az utóbbi csak akkor fordulhat elő, ha D 4-gyel osztva egyet ad maradékul, és u és v csak egyszerre lehet félegész.)
A Gauss-egészek normafogalma kézenfekvő módon általánosítható a kvadratikus egészek körében: normája . Kimutatható, hogy a kvadratikus egész gyűrűk ezzel a normával pontosan akkor euklidesziek, ha D = −11, −7, −3, −2, −1, 2, 3, 5, 6, 7, 11, 13, 17, 19, 21, 29, 33, 37, 41, 57 vagy 73.[137][138]
Elképzelhető persze, hogy a kvadratikus egészek gyűrűje valamilyen, a fentiektől különböző D értékre is euklideszi gyűrű valamilyen más normával. Nem ismert, hogy mely D-kre található ilyen euklideszi norma,[139] de egy 1994-es eredmény szerint D = 69-re a kvadratikus egészek euklideszi gyűrűt alkotnak.[139] Weinberger 1973-ban bizonyította, hogy D>0 esetén a kvadratikus gyűrűk pontosan akkor euklidesziek, ha főideálgyűrűk, feltéve, hogy az általánosított Riemann-hipotézis teljesül.[106]
Nem kommutatív gyűrűk[szerkesztés]
Nem kommutatív gyűrűkben is alkalmazható az euklideszi algoritmus, például a Hurwitz-kvaternióknál.[140] Legyen α és β a gyűrű két eleme. Ekkor δ jobb oldali közös osztó, ha van ξ és η eleme a gyűrűnek, hogy α = ξδ és β = ηδ. Hasonlóan, δ bal oldali közös osztó, ha α = δξ és β = δη. Mivel a szorzás nem kommutatív, az euklideszi algoritmus sem szimmetrikus, bal és jobb oldali változata van, a megfelelő oldali legnagyobb közös osztó keresésére.[141]
A jobb oldali változat első lépése:
- ρ0 = α − ψ0β = (ξ − ψ0η)δ
ahol ψ0 a hányados, és ρ0 a maradék. Az egyenlet szerint α és β jobb oldali közös osztói a ρ0 maradéknak is osztói.
A bal oldali változat hasonlóan kezdődik:
- ρ0 = α − βψ0 = δ(ξ − ηψ0) .
A következő lépésekben az elemek szerepe a kommutatív esethez hasonlóan változik, de itt végig a jobb vagy a bal változatot kell használni ahhoz, hogy megtaláljuk a jobb vagy a bal legnagyobb közös osztót.
Euklideszi tartományokban van az elemeknek olyan mérete, amely végig csökken. Ez biztosítja az algoritmus végességét, ha a méretek nem csökkenhetnek a végtelenségig.[142]
A legtöbb alkalmazás működik a nem kommutatív esetben is. A Bézout-lemma szerint a jobb és a bal legnagyobb közös osztó kifejezhető lineáris kombinációként, azaz vannak σ és τ gyűrűelemek, hogy a jobb legnagyobb közös osztó[143]
- Γright = σα + τβ
vagy a legnagyobb bal közös osztó
- Γleft = ασ + βτ .
Ezek felhasználhatók a diofantoszi egyenletek és a szimultán kongruenciarendszerek megoldásához. Ezen alapszik a négynégyzetszám-tétel egy bizonyítása kvaterniókkal.[142]
Története[szerkesztés]

Az euklideszi algoritmus az egyik legrégebb óta használt algoritmus.[144] Eukleidész Elemek című művében a 7. és a 10. könyv tartalmazza. A 7. könyvben a pozitív egész számok, a 10. kötetben a szakaszok euklideszi algoritmusát tárgyalja. Mai szóhasználattal ez a valós számokra vonatkozó algoritmus, azonban akkoriban csak a racionális számokkal foglalkoztak. A valós számokkal területet, térfogatot és egyebeket is jelölnek, amelyek nem válthatók át egymásba, és amelyekkel nem végezhető el az algoritmus. A szakaszok euklideszi algoritmusa geometriai, és a leghosszabb közös mértékegységet találja meg, ha van olyan.
Az algoritmust valószínűleg nem Eukleidész találta ki. Az Elemekben korának matematikai ismereteit gyűjtötte össze.[108][145] B. L. van der Waerden matematikus és történész szerint a 7. könyv számelméleti részei a pitagoreusoktól származnak.[146] Az algoritmus helyességét valószínűleg Knidoszi Eudoxosz bizonyította először Kr. e. 375 körül.[147][148] Az algoritmus valószínűleg Eudoxosz előtt is ismert volt,[149][150] az ἀνθυφαίρεσις szakkifejezés (anthyphairesis, kölcsönös kivonás) szakkifejezés alapján. Ez Arisztotelész és Eukleidész műveiben is megtalálható.[151]
Néhány évszázaddal később Kínában és Indiában is felfedezték az euklideszi algoritmust,[152] és használták diofantoszi egyenletek megoldására, amelyek a csillagászatból adódtak, hogy pontosabb naptárt készíthessenek. Árjabhata indiai csillagász és matematikus írta le az 5. század végén[153] a diofantoszi egyenletek megoldására.[154] A kínai maradéktétel egy speciális esetét a Szunce szuancsing () című mű írta le,[155] de a tétel általános leírását Csin Csiu-sao () adta 1247-es könyvében, amelynek címe Susu csiucsang () (數書九章, Értekezés a matematikáról kilenc részben).[156]
Európában sokáig csak az Elemek című műből ismerték az algoritmust. Bachet 1624-ben írt róla (Problèmes plaisants et délectables, második kiadás).[157] Leírta, hogy lánctörtbe fejtéshez és diofantoszi egyenletek megoldásához használják. A kibővített euklideszi algoritmusról az angol matematikus Nicholas Saunderson írt először, aki Roger Cotesnak tulajdonította, mint a lánctörtbe fejtés hatékony eszközét.[158]
A 19. században újabb számköröket vezettek be. Az euklideszi algoritmus hatékony eszköznek bizonyul a Gauss-egészek és az Eisenstein-egészek körében is. 1815-ben Carl Gauss az euklideszi algoritmussal bizonyította a Gauss-egészek egyértelmű felbontását, habár az eredményt csak 1832-ben jelentette meg.[120] Az 1801-ben kiadott Disquisitiones Arithmeticae csak a lánctörtekkel kapcsolatban említi meg az algoritmust.[159] Peter Gustav Lejeune Dirichlet-től származik az a kijelentés, hogy az euklideszi algoritmus a számelmélet nagy részének alapja.[160] Kimutatta, hogy az egyértelmű faktorizáció minden olyan számkörben teljesül, ahol az euklideszi algoritmus alkalmazható.[161] Számelméleti előadásait Richard Dedekind szerkesztette össze és bővítette ki. Dedekind az algoritmus segítségével tanulmányozta az algebrai egészeket, a számok új általános típusát. A Gauss-egészek egyértelmű felbontására alapozva bizonyította be a kétnégyzetszám-tételt.↑ Lejeune Dirichlet 1894: Definiálta az euklideszi gyűrű fogalmát. Az euklideszi gyűrűben nemcsak az igaz, hogy a faktorizáció egyértelmű, hanem van norma is. Ez biztosítja, hogy az euklideszi algoritmus véges. A 19. század végén Dedekind ideáljai háttérbe szorították az euklideszi algoritmust.[162]
Az algoritmus további alkalmazási lehetőségeit is feltárták a 19. században. Charles Sturm 1829-ben megmutatta, hogy a Sturm-láncok módszerében is hasznos a polinomok adott intervallumba eső valós gyökeinek kiszámításában.[163]
Az euklideszi algoritmus volt az első egészrelációs algoritmus, amellyel összemérhető számok közötti arányokat lehetett egészek közötti arányként meghatározni. Ezt később továbbiak követték, mint Helaman Ferguson és R.W. Forcade (1979) algoritmusa,[164] illetve a Lenstra–Lenstra–Lovász-algoritmus.[165][166]
1969-ben Cole és Davie egy kétszemélyes játékot alkotott az euklideszi algoritmusra alapozva, ez a The Game of Euclid.[167] Lényege, hogy a két kupac közül a kisebb többszöröseinek megfelelő számú követ lehet elvenni. Az nyer, akinek sikerül az egyik kupacot kiürítenie.[168][169] A játéknak van nyerő stratégiája.[170]
Jegyzetek[szerkesztés]
- ↑ A matematikus nevének szabatos átírása Eukleidész volna, tehát a szerkezet eukleidészi algoritmus, de ebben a kifejezésben hagyományosan rögzült euklideszi alakban (lásd például Püthagorasz, de Pitagorasz-tétel stb.).
- ↑ Stark 1978 16. o.
- ↑ Stark 1978 21. o.
- ↑ LeVeque 1996 32. o.
- ↑ LeVeque 1996 31. o.
- ↑ Grossman, J. W.. Discrete Mathematics. New York: Macmillan, 213. o. (1990). ISBN 0-02-348331-8
- ↑ Schroeder 2005 21–22. o.
- ↑ Schroeder 2005 216–219. o.
- ↑ Schroeder 2005 19. o.
- ↑ Excursions in number theory. New York: Oxford University Press, 27–29. o. (1966)
- ↑ LeVeque 1996 33. o.
- ↑ Stark 1978 25. o.
- ↑ Ore 1948 47–48. o.
- ↑ Stark 1978 18. o.
- ↑ Stark 1978 16-20. o.
- ↑ Knuth 1997 320. o.
- ↑ Discrete Mathematics: Elementary and Beyond. New York: Springer-Verlag, 100–101. o. (2003). ISBN 0-387-95584-4
- ↑ Kimberling, C. (1983). „A Visual Euclidean Algorithm”. Mathematics Teacher 76, 108–109. o.
- ↑ Cohn 1962 104–110. o.
- ↑ Ore 1948 43. o.
- ↑ a b Stewart, B. M.. Theory of Numbers, 2nd, New York: Macmillan, 43–44. o. (1964)
- ↑ Ore 1948 43. o.
- ↑ Lazard, D. (1977). „Le meilleur algorithme d'Euclide pour K[X] et Z”. Comptes Rendus Acad. Sci. Paris 284, 1–4. o.
- ↑ a b Shallit, J. (1994). „Origins of the analysis of the Euclidean algorithm”. Historia Math. 21, 401–419. o. DOI:10.1006/hmat.1994.1031.
- ↑ Knuth 1997 339–364. o.
- ↑ Reynaud, A.-A.-L.. Traité d'arithmétique à l'usage des élèves qui se destinent à l'École Polytechnique, 6th, Paris: Courcier (1811) As cited by (Shallit 1994).
- ↑ Finck, P.-J.-E.. Traité élémentaire d'arithmétique à l'usage des candidats aux écoles spéciales. Derivaux (1841)
- ↑ Lamé, G. (1844). „Note sur la limite du nombre des divisions dans la recherche du plus grand commun diviseur entre deux nombres entiers”. Comptes Rendus Acad. Sci. 19, 867–870. o.
- ↑ Grossman, H. (1924). „On the Number of Divisions in Finding a G.C.D”. The American Mathematical Monthly 31 (9), 443. o. DOI:10.2307/2298146.
- ↑ Honsberger, R.. Mathematical Gems II. The Mathematical Association of America, 54–57. o. (1976). ISBN 0-88385-302-7
- ↑ Knuth 1997 257-261. o.
- ↑ Crandall-Pomerance 2001 77–79, 81–85, 425–431. o.
- ↑ a b Möller, N. (2008). „On Schönhage's algorithm and subquadratic integer gcd computation”. Mathematics of Computation 77 (261), 589–607. o. DOI:10.1090/S0025-5718-07-02017-0.
- ↑ Knuth 1997 344. o.
- ↑ Ore 1948 45. o.
- ↑ Knuth 1997 344. o.
- ↑ Knuth 1997 343. o.
- ↑ Mollin 2008 21. o.
- ↑ Mollin 2008 21. o.
- ↑ LeVeque 1996 35. o.
- ↑ Knuth 1997 343. o.
- ↑ Mollin 2008 21–22. o.
- ↑ Knuth 1997 344. o.
- ↑ Knuth 1997 353. o.
- ↑ Knuth 1997 357. o.
- ↑ Tonkov, T. (1974). „On the average length of finite continued fractions”. Acta Arithmetica 26, 47–57. o.
- ↑ Weisstein, Eric W.: Porter's Constant (angol nyelven). Wolfram MathWorld
- ↑ Porter, J. W. (1975). „On a Theorem of Heilbronn”. Mathematika 22, 20–28. o. DOI:10.1112/S0025579300004459.
- ↑ Knuth, D. E. (1976). „Evaluation of Porter's Constant”. Computers and Mathematics with Applications 2 (2), 137–139. o. DOI:10.1016/0898-1221(76)90025-0.
- ↑ Dixon, J. D. (1970). „The Number of Steps in the Euclidean Algorithm”. J. Number Theory 2 (4), 414–422. o. DOI:10.1016/0022-314X(70)90044-2.
- ↑ Heilbronn, H. A..szerk.: Paul Turán: On the Average Length of a Class of Finite Continued Fractions, Number Theory and Analysis. New York: Plenum, 87–96. o. (1969)
- ↑ Knuth 1997 354. o.
- ↑ a b Norton, G. H. (1990). „On the Asymptotic Analysis of the Euclidean Algorithm”. Journal of Symbolic Computation 10, 53–58. o. DOI:10.1016/S0747-7171(08)80036-3.
- ↑ Knuth 1997 355. o.
- ↑ Knuth 1997 356. o.
- ↑ Knuth 1997 257-261. o.
- ↑ Knuth 1997 352. o.
- ↑ Wagon, S.. Mathematica in Action. New York: Springer-Verlag, 335–336. o. (1999). ISBN 0-387-98252-3
- ↑ Cohen 1993 14. o.
- ↑ Sorenson, Jonathan P.. High primes and misdemeanours: lectures in honour of the 60th birthday of Hugh Cowie Williams, Fields Institute Communications. Providence, RI: American Mathematical Society, 327–340. o. (2004) „The algorithms that are used the most in practice today [for computing greatest common divisors] are probably the binary algorithm and Euclid's algorithm for smaller numbers, and either Lehmer's algorithm or Lebealean's version of the k-ary GCD algorithm for larger numbers.”
- ↑ Schroeder 2005 21–22. o.
- ↑ Schroeder 2005 216–219. o.
- ↑ Knuth 1997 321-323. o.
- ↑ Stein, J. (1967). „Computational problems associated with Racah algebra”. Journal of Computational Physics 1 (3), 397–405. o. DOI:10.1016/0021-9991(67)90047-2.
- ↑ Crandall-Pomerance 2001 77–79, 81–85, 425–431. o.
- ↑ Knuth 1997 1328. o.
- ↑ Lehmer, D. H. (1938). „Euclid's Algorithm for Large Numbers”. The American Mathematical Monthly 45 (4), 227–233. o. DOI:10.2307/2302607.
- ↑ Sorenson, J. (1994). „Two fast GCD algorithms”. J. Algorithms 16, 110–144. o. DOI:10.1006/jagm.1994.1006.
- ↑ The Design and Analysis of Computer Algorithms. New York: Addison–Wesley, 300–310. o. (1974). ISBN 0-201-00029-6
- ↑ Schönhage, A. (1971). „Schnelle Berechnung von Kettenbruchentwicklungen”. Acta Informatica 1 (2), 139–144. o. DOI:10.1007/BF00289520.
- ↑ Cesari, G..szerk.: G. Buhler: Parallel implementation of Schönhage's integer GCD algorithm, Algorithmic Number Theory: Proc. ANTS-III, Portland, OR, Lecture notes in Computer Science. New York: Springer-Verlag, 64–76. o. (1998)
- ↑ Gal's accurate tables method revisited, Proceedings of the 17th IEEE Symposium on Computer Arithmetic (ARITH-17). Los Alamitos, CA: IEEE Computer Society Press (2005)
- ↑ Crandall-Pomerance 2001 77–79, 81–85, 425–431. o.
- ↑ Knuth 1997 319–320. o.
- ↑ Stillwell 1997 14. o.
- ↑ Knuth 1997 319–320. o.
- ↑ Bezout's Identity, Elementary Number Theory. New York: Springer-Verlag, 7–11. o. (1998)
- ↑ Rosen 2000 81. o.
- ↑ Cohn 1962 104. o.
- ↑ Rosen 2000 91. o.
- ↑ LeVeque 1996 33. o.
- ↑ Schroeder 2005 23. o.
- ↑ Rosen 2000 90–93. o.
- ↑ a b Koshy, T.. Elementary Number Theory with Applications. Burlington, MA: Harcourt/Academic Press, 167–169. o. (2002). ISBN 0-12-421171-2
- ↑ Algorithmic number theory. Cambridge, MA: MIT Press, 70–73. o. (1996). ISBN 0-262-02405-5
- ↑ Stark 1978 26–36. o.
- ↑ Ore 1948 44. o.
- ↑ Ore 1948 44. o.
- ↑ Stark 1978 281–292. o.
- ↑ Rosen 2000 119–125. o.
- ↑ Schroeder 2005 106–107. o.
- ↑ Schroeder 2005 108–109. o.
- ↑ Rosen 200 120–121. o.
- ↑ Stark 1978 47. o.
- ↑ Rosen 2000 143–170. o.
- ↑ Schroeder 2005 194–195. o.
- ↑ Concrete mathematics. Addison-Wesley, 123. o. (1989)
- ↑ Vinogradov, I. M.. Elements of Number Theory. New York: Dover, 3–13. o. (1954)
- ↑ Crandall-Pomerance 2001 225–349. o.
- ↑ Knuth 1997 369–371. o.
- ↑ Shor, P. W. (1997). „Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer”. SIAM Journal on Scientific and Statistical Computing 26, 1484. o. DOI:10.1137/s0097539795293172.
- ↑ Dixon, J. D. (1981). „Asymptotically fast factorization of integers”. Math. Comput. 36 (153), 255–260. o. DOI:10.2307/2007743.
- ↑ Lenstra, H. W., Jr. (1987). „Factoring integers with elliptic curves”. Annals of Mathematics 126 (3), 649–673. o. DOI:10.2307/1971363.
- ↑ Knuth 1997 380–384. o.
- ↑ a b c Lang, S.. Algebra, 2nd, Menlo Park, CA: Addison–Wesley, 190–194. o. (1984). ISBN 0-201-05487-6
- ↑ a b Weinberger, P.. „On Euclidean rings of algebraic integers”. Proc. Sympos. Pure Math. 24, 321–332. o.
- ↑ Stillwell 2003 151–152. o.
- ↑ a b Weil, A.. Number Theory. Boston: Birkhäuser, 4–6. o. (1983). ISBN 0-8176-3141-0
- ↑ A History of Mathematics, 2nd, New York: Wiley, 116–117. o. (1991). ISBN 0-471-54397-7
- ↑ Cajori, F,. A History of Mathematics. New York: Macmillan, 70. o. (1894). ISBN 0-486-43874-0
- ↑ Joux, Antoine. Algorithmic Cryptanalysis. CRC Press, 33. o. (2009). ISBN 9781420070033
- ↑ Mathematical Omnibus: Thirty Lectures on Classic Mathematics. American Mathematical Society, 13. o. (2007). ISBN 9780821843161
- ↑ Darling, David. The Universal Book of Mathematics: From Abracadabra to Zeno's Paradoxes. John Wiley & Sons, 175. o. (2004). ISBN 9780471667001
- ↑ Williams, Colin P.. Explorations in Quantum Computing. Springer, 277–278. o. (2010). ISBN 9781846288876
- ↑ Cox-Little-O'Shea 1997 37–46. o.
- ↑ Schroeder 2005 254–259. o.
- ↑ Grattan-Guinness, Ivor. Convolutions in French Mathematics, 1800-1840: From the Calculus and Mechanics to Mathematical Analysis and Mathematical Physics. Volume II: The Turns, Science Networks: Historical Studies. Basel, Boston, Berlin: Birkhäuser, 1148. o. (1990). ISBN 9783764322380 „Our subject here is the 'Sturm sequence' of functions defined from a function and its derivative by means of Euclid's algorithm, in order to calculate the number of real roots of a polynomial within a given interval”
- ↑ Solving Ordinary Differential Equations I: Nonstiff Problems, 2nd, Springer Series in Computational Mathematics, Springer, 81ff. o. (1993). ISBN 9783540566700
- ↑ Stillwell 2003 101–116. o.
- ↑ a b Gauss, C. F. (1832). „Theoria residuorum biquadraticorum”. Comm. Soc. Reg. Sci. Gött. Rec. 4. Reprinted in Gauss, C. F.. Werke. Cambridge Univ. Press, 65–92. o.. doi:10.1017/CBO9781139058230.004 and doi:10.1017/CBO9781139058230.005 (2011)
- ↑ Stillwell 2003 101–116. o.
- ↑ a b c Hensley, Doug. Continued Fractions. World Scientific, 26. o. (2006). ISBN 9789812564771
- ↑ Dedekind, Richard. Theory of Algebraic Integers, Cambridge Mathematical Library. Cambridge University Press, 22–24. o. (1996). ISBN 9780521565189
- ↑ Numbers and Symmetry: An Introduction to Algebra. CRC Press, 44. o. (1997). ISBN 9780849303012
- ↑ Introduction to Number Theory. Prentice-Hall (1976). ISBN 9780134912820 „State and prove an analogue of the Chinese remainder theorem for the Gaussian integers.”
- ↑ Stark 1978 290. o.
- ↑ Cohn 1962 104–105. o.
- ↑ Lauritzen, Niels. Concrete Abstract Algebra: From Numbers to Gröbner Bases. Cambridge University Press, 130. o. (2003). ISBN 9780521534109
- ↑ (Lauritzen 2003), p. 161
- ↑ (Lauritzen 2003), p. 132
- ↑ Sharpe, David. Rings and Factorization. Cambridge University Press, 55. o. (1987). ISBN 9780521337182
- ↑ (Sharpe 1987), p. 52
- ↑ (Lauritzen 2003), p. 131
- ↑ Stillwell 2003 101–116. o.
- ↑ Lamé, G. (1847). „Mémoire sur la résolution, en nombres complexes, de l'équation An + Bn + Cn = 0”. J. Math. Pures Appl. 12, 172–184. o.
- ↑ Edwards, H.. Fermat's last theorem: a genetic introduction to algebraic number theory. Springer, 76. o. (2000)
- ↑ Cohn 1962 104–110. o.
- ↑ LeVeque, W. J.. Topics in Number Theory, Volumes I and II. New York: Dover Publications, II:57,81. o. [1956] (2002). ISBN 978-0-486-42539-9
- ↑ a b Clark, D. A. (1994). „A quadratic field which is Euclidean but not norm-Euclidean”. Manuscripta Mathematica 83, 327–330. o. DOI:10.1007/BF02567617. [halott link]
- ↑ Stillwell 2003 151–152. o.
- ↑ Stillwell 2003 151–152. o.
- ↑ a b Elementary Number Theory, Group Theory and Ramanujan Graphs, London Mathematical Society Student Texts. Cambridge University Press, 59–70. o. (2003). ISBN 9780521531436
- ↑ Ribenboim, Paulo. Classical Theory of Algebraic Numbers, Universitext. Springer-Verlag, 104. o. (2001). ISBN 9780387950709
- ↑ Knuth 1997 318. o.
- ↑ Jones, A.. Greek mathematics to AD 300, Companion encyclopedia of the history and philosophy of the mathematical sciences. New York: Routledge, 46–48. o. (1994). ISBN 0-415-09238-8
- ↑ van der Waerden, B. L.. Science Awakening, translated by Arnold Dresden. Groningen: P. Noordhoff Ltd, 114–115. o. (1954)
- ↑ Knuth 1997 318. o.
- ↑ von Fritz, K. (1945). „The Discovery of Incommensurability by Hippasus of Metapontum”. Annals of Mathematics 46 (2), 242–264. o. DOI:10.2307/1969021.
- ↑ Heath, T. L.. Mathematics in Aristotle. Oxford Press, 80–83. o. (1949)
- ↑ Fowler, D. H.. The Mathematics of Plato's Academy: A New Reconstruction. Oxford: Oxford University Press, 31–66. o. (1987). ISBN 0-19-853912-6
- ↑ Becker, O. (1933). „Eudoxus-Studien I. Eine voreuklidische Proportionslehre und ihre Spuren bei Aristoteles und Euklid”. Quellen und Studien zur Geschichte der Mathematik B 2, 311–333. o.
- ↑ Stillwell 1997 31. o.
- ↑ Tattersall 2005 70. o.
- ↑ Rosen 2000 86–87. o.
- ↑ Ore 1948 247–248. o.
- ↑ Tattersall 2005 72, 184–185. o.
- ↑ Tattersall 2005 70. o.
- ↑ Tattersall 2005 72–76. o.
- ↑ Stillwell 1997 31. o.
- ↑ Stillwell 1997 31–32. o.
- ↑ Lejeune Dirichlet 1894 29–31. o.
- ↑ Stillwell 2003 41–42. o.
- ↑ Sturm, C. (1829). „Mémoire sur la résolution des équations numériques”. Bull. des sciences de Férussac 11, 419–422. o.
- ↑ Weisstein, Eric W.: Integer Relation (angol nyelven). Wolfram MathWorld
- ↑ Peterson, I. (2002. augusztus 12.). „Jazzing Up Euclid's Algorithm”. ScienceNews.
- ↑ Cipra, B. A. (2000. május 16.). „The Best of the 20th Century: Editors Name Top 10 Algorithms”. SIAM News 33 (4), Kiadó: Society for Industrial and Applied Mathematics. [2016. szeptember 22-i dátummal az eredetiből archiválva]. (Hozzáférés: 2016. augusztus 13.)
- ↑ (1969) „A game based on the Euclidean algorithm and a winning strategy for it”. Math. Gaz. 53 (386), 354–357. o. DOI:10.2307/3612461.
- ↑ Rosen 2000 95. o.
- ↑ Roberts, J.. Elementary Number Theory: A Problem Oriented Approach. Cambridge, MA: MIT Press, 1–8. o. (1977). ISBN 0-262-68028-9
- ↑ Spitznagel, E. L. (1973). „Properties of a game based on Euclid's algorithm”. Math. Mag. 46 (2), 87–92. o. DOI:10.2307/2689037.
Források[szerkesztés]
- ↑ Knuth 1994: D. E. Knuth: A számítógépprogramozás művészete 1. Alapvető algoritmusok, Műszaki Könyvkiadó, Budapest, 2. kiadás, 1994, ISBN 963 1600750, 25–34. o.
- ↑ Cohen 1993: Cohen, H.. A Course in Computational Algebraic Number Theory. New York: Springer-Verlag (1993). ISBN 0-387-55640-0
- ↑ Cohn 1962: Cohn, H.. Advanced Number Theory. New York: Dover (1962). ISBN 0-486-64023-X
- ↑ Cox-Little-O'Shea 1997: Ideals, Varieties, and Algorithms: An Introduction to Computational Algebraic Geometry and Commutative Algebra, 2nd, Springer-Verlag (1997). ISBN 0-387-94680-2
- ↑ Crandall-Pomerance 2001: Prime Numbers: A Computational Perspective, 1st, New York: Springer-Verlag (2001). ISBN 0-387-94777-9
- ↑ Lejeune Dirichlet 1894: Lejeune Dirichlet, P. G.. Vorlesungen über Zahlentheorie (Lectures on Number Theory) (német nyelven). Braunschweig: Vieweg (1894). OCLC 490186017. See also Vorlesungen über Zahlentheorie
- ↑ Knuth 1997: Knuth, D. E.. The Art of Computer Programming, Volume 2: Seminumerical Algorithms, 3rd, Addison–Wesley (1997). ISBN 0-201-89684-2
- ↑ LeVeque 1996: LeVeque, W. J.. Fundamentals of Number Theory. New York: Dover [1977] (1996). ISBN 0-486-68906-9
- ↑ Mollin 2008: Mollin, R. A.. Fundamental Number Theory with Applications, 2nd, Boca Raton: Chapman & Hall/CRC (2008). ISBN 978-1-4200-6659-3
- ↑ Ore 1948: Ore, O.. Number Theory and Its History. New York: McGraw–Hill (1948)
- ↑ Rosen 2000: Rosen, K. H.. Elementary Number Theory and its Applications, 4th, Reading, MA: Addison–Wesley (2000). ISBN 0-201-87073-8
- ↑ Schroeder 2005: Schroeder, M.. Number Theory in Science and Communication, 4th, Springer-Verlag (2005). ISBN 0-387-15800-6
- ↑ Stark 1978: Stark, H.. An Introduction to Number Theory. MIT Press (1978). ISBN 0-262-69060-8
- ↑ Stillwell 1997: Stillwell, J.. Numbers and Geometry. New York: Springer-Verlag (1997). ISBN 0-387-98289-2
- ↑ Stillwell 2003: Stillwell, J.. Elements of Number Theory. New York: Springer-Verlag (2003). ISBN 0-387-95587-9
- ↑ Tattersall 2005: Tattersall, J. J.. Elementary Number Theory in Nine Chapters. Cambridge: Cambridge University Press (2005). ISBN 978-0-521-85014-8
Fordítás[szerkesztés]
- Ez a szócikk részben vagy egészben az Euclidean algorithm című angol Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.



















































![{\displaystyle {\frac {a}{b}}=q_{0}+{\cfrac {1}{q_{1}+{\cfrac {1}{q_{2}+{\cfrac {1}{\ddots +{\cfrac {1}{q_{N}}}}}}}}}=[q_{0};q_{1},q_{2},\ldots ,q_{N}]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfd6202ce1dc46510c7894abba456c3b899c58bf)
![{\displaystyle {\frac {1071}{462}}=2+{\cfrac {1}{3+{\cfrac {1}{7}}}}=[2;3,7]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41bb1b741861a853bc9f7bcbcd91315b07ffdac0)



