Helyvektor
A matematikában a sík vagy a tér egy adott pontjának helyvektora az a vektor, amely a koordináta-rendszer origójából (kezdőpontjából) a pontba mutat. A helyvektor tehát függ attól, hogy a pontot milyen koordináta-rendszerben helyezzük el.
A koordináta-rendszer vagy vonatkoztatási rendszer origója az a pont, amelynek minden koordinátája 0. Egy derékszögű koordináta-rendszerben ez a koordináta-tengelyek metszéspontja. Egy pont helyvektora az vektor, ahol az origó.
A helyvektor előállítása[szerkesztés]
A geometriában szokásos még az adott pont nevének kisbetűvel írása és felülvonással ellátva jelölni az adott pont helyvektorát, például:
Szokás még az adott pont betűjelét nyíllal ellátva jelölni a helyvektort:
A kinematikában egy anyagi pontot az r(t) helyvektor jelöli, amely megmutatja a t időpontbeli helyét, elmozdulását. Az r helyvektor a Descartes-féle koordináta-rendszerben:
ahol x(t), y(t), z(t) az r helyvektor koordinátái, i, j, k pedig - az origóban egymásra merőlegesen álló - így a koordináta-rendszert "kifeszítő" egységvektorok. (Egységvektor: 1 egységnyi hosszúságú vektor).
Ennek ismeretében bármikor meghatározható a tömegpont pályája.
(A kinematika a mechanika mozgásokkal foglalkozó része, nem vizsgálja az erőt, amely a mozgásokat befolyásolja, azt a kinetika, a mechanika egy másik részterülete tárgyalja.)
Példák és geometriai alkalmazások[szerkesztés]
Összekötő vektor[szerkesztés]
Legyenek és az euklideszi tér pontjai! Ekkor a összekötő vektor megkapható a és helyvektorok segítségével:
Descartes-koordináták[szerkesztés]
Legyenek a pont koordinátái ! Ekkor az helyvektor koordinátái:
Hasonlók teljesülnek más dimenziókban is.
Eltolás[szerkesztés]
Jelölje egy párhuzamos eltolás vektorát, és jelölje az eltolásban az pont képét ! Ekkor
Origó körüli forgatás[szerkesztés]
Egy origó körüli szögű forgatás a Descartes-koordinátákban leírható mátrixszal: Ha egy pont helyvektora, és az képpont helyvektora, akkor:
Affin leképezés[szerkesztés]
Egy általános affin leképezés, ami az pontot az pontra képezi le, helyvektorokkal a következőképpen ábrázolható:
ahol az helyvektora, az helyvektora, egy lineáris leképezés, és egy eltolás vektora. Descartes-koordinátákban az lineáris leképezés ábrázolható egy mátrixszal, és teljesül, hogy:
Három dimenzióban:
Más dimenziókban az ábrázolás hasonló.
Egyenes paraméteres ábrázolása[szerkesztés]
A és pontokon áthaladó egyenes pontosan azokat az pontokat tartalmazza, melyek helyvektora előáll, mint
- ahol
Ez az egyenes egyenletének paraméteres alakja.
Az egyenes egyenletének normálformája[szerkesztés]
Egy támaszponton átmenő, normálvektorú sík pontosan azokat az pontokat tartalmazza, amelyek helyvektora eleget tesz az
normálegyenletnek. Itt a támasztópont helyvektora, és a szorzópont skalárszorzást jelöli.
Helyvektorok különböző koordináta-rendszerekben[szerkesztés]
Egy helyvektorral leírt pont kifejezhető különböző koordináta-rendszerekben, ahol a helyvektor vonatkoztatási pontja rendszerint az origó.
Descartes-koordináták[szerkesztés]
Descsartes-féle koordináta-rendszerben a helyvektor koordinátái
Így a Descartes-koordináták egyben a helyvektor koordinátái is.
Hengerkoordináták[szerkesztés]
A hengerkoordináták alapján a helyvektor koordinátái a megfelelő Descartes-koordináták:
ahol a pont távolsága a -tengelytől, a szöget az x tengely felől az y tengely felé mérjük. Tehát a és koordináták az - síkra vetített pontok polárkoordinátái.
Itt egy leképezésről van szó, ami a koordinátákhoz hozzárendeli a helyvektor koordinátáit.
Gömbkoordináták[szerkesztés]
Gömbkoordinátákban adott pont esetén is át kell számolni a koordinátákat a megfelelő Descartes-koordinátákba:
ahol az origótól mért távolság, a szög az - síkban az -tengelytől az -tengely irányába mért szög, a szög pedig a -tengely és a helyvektor által bezárt szög.
Kísérő triéder[szerkesztés]
Egy felületen vagy görbén történő mozgást pályához kötött koordináta-rendszerben, a kísérő triéderben (más néven természetes koordináta-rendszer-ben) ábrázolnak, amit három, egymásra kölcsönösen merőleges egységvektor alkot. Az egységvektorai: t az érintő (tangenciális), n a főnormális és b, a binormális egységvektor.
A kísérő triéder előállítása a következő:
- A kísérő triéder egységvektorai:
- az érintő (tangenciális, e -vel is jelölhetik),
- a főnormális és
- a binormális egységvektor (azaz a másik két egységvektor vektoriális szorzata).
A kísérő triéder fogalmának a kinematikában van jelentősége. Pl. a Frenet-formulák, azaz a térgörbe kísérő triédere három egységvektorának az ívhossz (s) szerinti deriváltjait megadó összefüggések:
- t′(s) = g(s)n(s),
- n′(s) = –g(s)t(s) + c(s)b(s),
- b′(s) = –c(s)n(s),
ahol g(s) a görbe görbülete és c(s) a torziója.
A helyvektor deriváltjai (sebességvektor, gyorsulásvektor)[szerkesztés]
Sebességvektor[szerkesztés]
A helyvektor idő szerinti első deriváltja (differenciálhányadosa) a sebesség (velocitas), jele: v, mértékegysége: méter per szekundum vagy méter per másodperc (m/s).
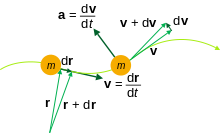
r a helyvektora, v a sebességvektora, a a gyorsulásvektora.
A sebességvektor a pálya érintőjének az irányába mutat.
A Descartes-féle koordináta-rendszerben:
Gyorsulásvektor[szerkesztés]
A gyorsulás a helyvektornak az idő szerinti második, a sebességnek pedig az idő szerinti első deriváltja, jele: a (acceleratio), mértékegysége: méter per szekundumnégyzet (másként: méter per másodperc a négyzeten): m/s² vagy m*s−2:
Az átlagos gyorsulásvektor iránya megegyezik a Δv sebességváltozás-vektor irányával. Az átlagos gyorsulás független attól, hogyan változik az anyagi pont sebessége a kezdő és végpont között, kizárólag a sebesség vektornak a két pontban felvett értékétől (azok különbségétől) és az időintervallum hosszától függ. Az anyagi pont pillanatnyi gyorsulását az átlaggyorsulás határértéke adja, ha Δt tart a nullához.
További deriváltak[szerkesztés]
További deriváltakat már nem szoktak keresni. Az ok: az anyagi pontnak a környezetével való kölcsönhatását - az erőt - Nevton II. törvénye a helyvektor második deriváltjával, a gyorsulással kapcsolja össze:
ahol F az erő, m a tömeg és a a gyorsulás.
A h vektor, a helyvektor idő szerinti harmadik deriváltja például a nagy sebességű íves vasúti pályák geometriai pályáját határozza meg, valamint előidézi a élettani hatásokat, egyben e hatások mértéke is:
Az m vektort, a helyvektor idő szerinti negyedik deriváltját pedig - a vasútnál maradva - a nagy sebességű vasúti pályák geometriai összehasonlító értékelésénél alkalmazzák a mérnökök:
Források[szerkesztés]
- Helyvektor
- Az anyagi pont kinematikája
- FIZIKA I. Mechanika, Hőtan - Kinematika
- Mechanika III.
- II. Mechanika[halott link]
- Dr. Megyeri Jenő. Vasúti mozgásgeometria. Budapest: Műszaki Könyvkiadó (1986). ISBN 9631059782
- Természettudományi lexikon II. (D–G). Főszerk. Erdey-Grúz Tibor. Budapest: Akadémiai. 1965. 752. o.
- kísérő triéder (szócikk), TermTudLex. Budapest: Akadémiai Kiadó, 3. kötet, 729. o. (1966)
- Klaus Desch: Mathematische Ergaenzungen zur Physik II, Kapitel 11: Vektoranalysis. (PDF, 210 kB). Institut für Experimentalphysik, Hamburg.
Fordítás[szerkesztés]
Ez a szócikk részben vagy egészben az Ortsvektor című német Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.

























































