Fogalomírás
„Fogalomírásomnak az élet nyelvéhez való viszonyát, úgy vélem, azzal világíthatom meg a legjobban, ha a mikroszkópnak a szemhez való viszonyával vetem össze. Utóbbi … nagy fölényben van a mikroszkóppal szemben. Amikor azonban tudományos célok nagy követelményeket támasztanak a megkülönböztetés élességével szemben, a szem elégtelennek bizonyul. A mikroszkóp viszont ilyen célokra a legtökéletesebben megfelel, de épp ezért minden másra hasznavehetetlen. Hasonlóképpen a jelen fogalomírás is egy meghatározott tudományos célra kigondolt segédeszköz, amelyet nem szabad amiatt elítélni, hogy másra nem alkalmas …
Ha a filozófia feladata, hogy megtörje a szó uralmát az emberi szellem felett […], úgy fogalomírásom, ezekre a célokra továbbfejlesztve, hasznos eszközzé válhat a filozófusok számára. […] Úgy vélem, hogy a logikát már ezen fogalomírás feltalálása is előmozdította. Remélem, hogy a logikusok, ha nem riadnak vissza az idegenszerűség első benyomásától, nem tagadják meg majd egyetértésüket azoktól az újításoktól, melyekre engem a tárgyban bennerejlő szükségszerűség késztetett. Ezek az eltérések a megszokottól abban lelik igazolásukat, hogy a logika mindeddig még túl szorosan kapcsolódott a nyelvhez és a nyelvtanhoz. Különösen a szubjektum, ill. predikátum fogalmának az argumentum, ill. függvény fogalmával való helyettesítését vélem maradandónak …” (Frege: Fogalomírás [Előszó]).
A Fogalomírás, más néven Begriffsschrift Gottlob Frege jénai matematikus 1879-ben írt műve, illetve a műben kidolgozott formális elmélet (formális nyelv) a matematikai logika számára. A mű eredeti, teljes német címe Begriffsschrift, eine der aritmetischen nachgebildete Formelsprache des reinen Denkens, azaz Fogalomírás, a tiszta gondolkodás aritmetikai mintára alapozott formulanyelve.[1]
Frege ebben dolgozta ki a matematikai logika első jelentősebb elméletét, az ún. elsőrendű predikátumlogikát (valójában Frege elmélete még bővebb is, mint az elsőrendű logika); ezzel az ókor (Arisztotelész, sztoikusok) óta, több ezer éve először történt alapvető, paradigmális változás a formális logika tudományában. A Frege által alkotott szimbolikus logikai formális nyelv, melyet szintén fogalomírásnak nevezünk, volt az első igazán jelentős példája az ilyesfajta nyelveknek.
A mű története[szerkesztés]
Tudomány- és eszmetörténeti (és egyéb) előzmények és motivációk[szerkesztés]
„Száz évvel ezelőtt, 1879-ben, vékonyka, mindössze 88 oldal terjedelmű könyv jelent meg Halléban. Szerzője dr. Friedrich Ludwig Gottlob Frege, a Jénai Egyetem 31 éves magántanára. A könyvecske címe: Begriffsschrift, eine der aritmetischen nachgebildete Formelsprache des reinen Denkens, magyarul: Fogalomírás. Eltekintve néhány recenziótól, a mű a századfordulóig teljesen észrevétlen maradt, és semmilyen hatást nem fejtett ki a tudomány fejlődésére. Pedig ez a könyv a 19. század utolsó harmadának egyik legjelentősebb szellemi alkotását tartalmazza. Ma már a Begriffsschrift megjelenési évét tekintik – teljes joggal – a modern logika (szimbolikus vagy matematikai logika) születési évének, míg a könyv szerzőjét – ugyancsak indokoltan – korunk Arisztotelészének.” (Ruzsa Imre: Logika, szemantika, matematika [Előszó]).
Frege 1874 óta volt a Jénai Egyetem fizetés nélküli magántanára, matematikai előadásokat tartott. Kollégája és volt tanára, Ernst Abbe meghívta Fregét rendkívüli kinevezett professzornak, többek között hogy segítsen annak nehéz anyagi helyzetén (bővebben) . A kinevezés feltételei közé ebben az időszakban szokásosan beletartozott az is, hogy a tanárjelölt egy tudományos munkát készítsen. Abbe azt javasolta Fregének, adja ki addigi logikai kutatásainak eredményeit, és az így keletkezett művel pályázzon a professzori állás megszerzésére. Frege így is tett, az elkészült munka, mely 1879-ben meg is jelent, a „Fogalomírás” címet kapta.
Egyesek Archiválva 2005. május 3-i dátummal a Wayback Machine-ben Frege művét úgy interpretálják, mint a sztoikus logika és az arisztotelészi kvantált kijelentések elméleteinek egyesítését (Richard Mendelsohn, 2002). Kétségtelen, hogy a Fogalomírásban végeredményképp ez (is) történik; azonban, noha a sztoikus logika újrafelfedezése is az 1800-as évek végére esik, nem bizonyított, hogy Frege művének szintézis volta szó szerint is igaz, azaz a szerző ismerte volna a sztoikusok elméleteit (sőt lehetséges, hogy az arisztotelészi logika helyett is csak a tradicionális logikát ismerte).
Bár a logika megújításának, egy calculus ratiocinator megalkotásának a gondolata még Leibniztől származik, az ennek megvalósítását célzó első komoly lépéseket csak két évszázad múlva tették meg a matematikusok. Az angol George Boole konstruált egy logikai algebrát, amelyet mások (köztük a német Ernst Schröder) módosítottak és továbbfejlesztettek; módszerét és kapacitását tekintve azonban a Boole–Schröder-algebra csak halvány előképe Leibniz gondolatainak, s e tekintetben összehasonlíthatatlan Frege művével. Noha vitatkozni lehet azon, hogy Frege gondolatai mennyire előzmény nélküliek, az biztos, hogy fogalomírása szinte tökéletes alkotás, amelynek alapjaihoz az azóta eltelt százegynéhány esztendő tartalmilag semmi lényegeset nem tett hozzá, pusztán Frege eredeti, szemléletes és meglehetősen áttekinthető jelölésrendszerét cserélték le (nyomdatechnikai okok miatt, elsősorban Russell) a mai, semmivel sem könnyebben olvasható jelrendszerre.
- „Meglepő lehet, hogy ez a fiatal tudós 30 éves korára ilyen nagy jelentőségű eredményhez jutott. Meglepődésünket csak fokozza az a tény, hogy a maga elé tűzött kutatási programjában egyáltalán nem szerepelt a logika megreformálásának gondolata” – írja Ruzsa Imre.
Valóban, a Fogalomírás alapgondolatai inkább bizonyos, még Immanuel Kant által felvetett, de valójában sokkal régebbi eredetű filozófiai problémákhoz kapcsolódnak, melyek a matematika fogalmainak és állításainak létére-tartalmára és természetére kérdeznek rá. Mint filozofikus hajlamú matematikus, Frege élénken érdeklődött diszciplínájának „végső alapjai” iránt, és mélységesen elégedetlen volt a korabeli felfogásokkal (utóbbiakról és Frege általi bírálatukról ld. Gottlob Frege: Az aritmetika alapjai). Arra a meggyőződésre jutott, hogy az aritmetika tisztán logikai tudomány, és céljául tűzte ki ennek szabatos bizonyítását.
- „A legbiztosabb nyilván a logikai bizonyítási mód […] ezért az olyan igazságokat, melyek megalapozást igényelnek, két típusba soroljuk: az egyik típusban a bizonyítás tisztán logikailag lehetséges, a másikban viszont tapasztalati tényekre kell támaszkodnia. Amikor azt a kérdést tettem fel magamnak, hogy az aritmetikai ítéletek melyik típusba tartoznak e kettő közül, először azt kellett megvizsgálnom, mennyire lehet jutni pusztán következtetésekkel az aritmetikában […]. Eljárásom az volt, hogy először megkísérlem a sorozaton belüli elrendezettség fogalmát a logikai következtetésekre visszavezetni, hogy innen a számfogalomhoz léphessek tovább. Hogy itt ne furakodjon be észrevétlenül valami szemléletes, azt teljesen a következtetésláncok hézagtalanságának kellett biztosítania. Miközben ezt a követelményt a legszigorúbban kielégíteni igyekeztem, akadályba ütköztem a nyelv elégtelenségében, amely […] annál kevésbé engedte elérnem azt a szabatosságot, amelyet célom megkívánt, minél bonyolultabbá váltak az összefüggések. Ebből a szükségszerűségből keletkezett a jelen Fogalomírás gondolata.” (Frege: Fogalomírás [Előszó])
Mivel a természetes nyelv és az erre mind tárgyában, mind formájában igencsak építő tradicionális logika alkalmatlannak bizonyult a matematikai definíciók és bizonyítások reprodukálására (kiegészítés vagy továbbfejlesztés nélkül ugyanilyen alkalmatlan a Boole–Schröder-algebra is), így a kitűzött feladat arra késztette, hogy – mellékfeladatként – olyan logikai eszközrendszert alkosson, aminek keretében a matematikai bizonyítások céljainak megfelelően elemezhetőek. Azonban, mint műve címe is mutatja, kezdettől fogva tisztában volt azzal, hogy logikája nem kizárólag a matematika logikájáé, hanem a szabatos gondolkodásé általában.
Egyesek (például Reuben Hersh) valószínűleg félreértették vagy félremagyarázták Fregének a fentemlített szabatos bizonyítási módszerrel és mellékfeladattal kapcsolatos céljait is (Hersh: A matematika természete; 155. o). Túlzott egyszerűsítés azt mondani, hogy Frege elsődleges és eredeti célja az volt, hogy „abszolút bizonyosságot” adjon a matematika állításainak (fundacionalizmus); az effajta, euklideszit meghaladó szigorúságról említést tesz ugyan, mint a korra általánosan jellemző „tünetről”, és egyet is ért vele; ezt és a leibnizi „univerzális kalkulus” megteremtését a mű Előszavában mégis csak mint nagyon távoli – még csak nem is célt, hanem inkább alkalmazási lehetőséget – azaz mint egyfajta esetleges következményt említi. Elsődleges céljaként még Az aritmetika alapjai c. művében sem ezt jelöli meg. Elsődleges célja egy filozófiai sejtés bizonyítása, azé, hogy a logika alkalmasan használható a fundacionalizmus céljaira (de egy fundacionalista elmélet kidolgozása nem célja volt a Fogalomírásnak, hanem inkább „mellékterméke”). Sőt a Fogalomírás és a hozzá szorosan kapcsolódó Az aritmetika alaptörvényei éppenséggel a pszichologista, formalista és empirista fundacionalizmus elleni vitairatban, Az aritmetika alapjaiban lefektetett filozófiai tételek tudományos igazolási kísérletének tekinthetőek. Tudománytörténetileg nem igazolható Hershnek az a feltevése, hogy Frege a „jobbos” matematikai fundacionalizmus („matematikai fundamentalizmus”?) mániákus úttörője – inkább egy a képviselői közül; egyszersmind ezen irányzat hiányosságainak és kezdetlegességének kritikusa, aki felhívta a figyelmet az óriási hibákra és fogalmi zavarra, de javasolt egy megoldást is.
A mű értékelése, fogadtatása régen és ma[szerkesztés]
Frege örömmel regisztrálhatta (és a mű Előszavában és második fejezete végén ezt meg is tette), hogy Fogalomírása magában foglalja nemcsak a tradicionális logika minden helytálló eredményét, hanem „tudja” annak nagy részét is, amit a Boole–Schröder-algebra tud, és ugyanakkor messze túlszárnyalja ezeket.
Éppen ezért nagyon is magyarázatra szorul a mű Frege számára óriási csalódást jelentető fogadtatása a szélesebb tudományos közönség körében, mivel műve nem keltett az eredmények fontossága alapján várt érdeklődést, annál inkább rosszallást; pedig a benne foglaltak matematikailag helyesek voltak (a mű mindössze két ismert – és nem túl lényeges – szakmai hibát vagy vitatható állítást tartalmaz); szakmai szempontból nemhogy sok kivetnivalót lehet benne találni, hanem inkább példamutatóan precíz. Hátrányos fogadtatásához többek között a mű egyik lényege, a Frege által bevezetett újszerű szimbólumrendszer is hozzájárult, és az is, hogy a fogalomírás (elég világosan megfogalmazott) céljait nem ismerték fel vagy nem értették meg. A megírása és megjelenése mindenesetre hozzásegítette Fregét a rendkívüli egyetemi tanári kinevezéshez, és ezzel, a biztosabb jövőkép megteremtésén keresztül, a nyugodt alkotó- és kutatómunkához. Egyúttal pedig megszületett a modern matematikai logika addigi legjobban kidolgozott elmélete is.
A Begriffsschriftről megjelenése után egy év alatt hat recenziót közöltek különböző mértékadó tudományos folyóiratok. Ezeket összegyűjtötte és angolra fordítva közreadta T. W. Bynum az általa szerkesztett, bevezetett és fordított kötet függelékében: Gottlob Frege, Conceptual Notation and Related Articles (Oxford: Clarendon, 1972. Appendix I.). Frege művét egy-egy tekintélyes francia és angol filozófiai folyóirat is szemlézte, ami elsőkönyves szerző esetében több mint kielégítő eredmény; noha a recenziók többségének hangneme inkább kritikus, mint elismerő, és utóbbi jellegű vélemények is inkább a recenzens jóindulatáról, mintsem a könyv megértéséről tanúskodnak. Minden recenzens úgy olvasta a könyvet, hogy az a Boole-féle logikai algebrát akarja felváltani egy jobb jelölésmóddal, és a többség úgy ítélt, hogy Frege formulanyelve ugyan önmagában megáll, és kétségtelenül eredeti alkotás, de a Boole-éhoz képest nehézkes és kényelmetlen alkalmatosság. Frege, aki könyvében egyetlen szót sem veszteget a booliánus logikára, most két tanulmányban is részletesen kifejti hozzá való viszonyát, de egyik sem jut nyilvánossághoz, a folyóiratok visszautasítják közlését. A könyvnek eme sikertelenség és sikeresség között ingadozó státusza indítja Fregét Az aritmetika alapjai c. műve megírására, melyben köznapi ember (és más tudósok) számára is „megmagyarázza” matematikai munkái célját.
A Fogalomírásban megalkotott fogalomírást Frege később jelentős mértékben továbbfejlesztette, mind annak filozófiai alapjait tekintve, de a szimbólumrendszert is bővítette, és egy-két alapszimbólum jelentésén is változtatott. A módosított fogalomírás Az aritmetika alaptörvényei c. művében jelent meg 1893-ban.
„Nemrégiben G. Cantor egy figyelemre méltó írásában végtelen számosságokat vezetett be. Teljesen egyetértek vele annak a nézetnek az értékelésében, miszerint egyáltalában csak a véges számosságok számítanak valóságos- nak. […] Miközben ebben a kérdésben, úgy vélem, egyetértek Cantorral, a megnevezésben viszont eltérek tőle. Az én számosságomat ő »kardinális számnak« nevezi, míg az ő számosság- fogalma a rendezésre is tekintettel van. […] Úgy tűnik nekem, a szukcesszióban való követés és a Cantor-féle számosság pontos definíciója még hiányzik. Ezért hivatkozik Cantor a kissé titokzatos »belső szemléletre« ott, ahol kívánatos és alighanem lehetséges is volna a definíciókon alapuló bizonyítás. Úgy gondolom ugyanis, előre látható, hogyan lehet ezeket a fogalmakat meghatározni. Semmi esetre sem akarom viszont a fenti megjegyzésekkel a jogosultságukat támadni. Ellenkezőleg, ezekben a vizsgálatokban a tudomány kibővítését üdvözlöm […] ” (Frege: Az aritmetika alapjai, IV. f.; 86. §.).
A Fogalomírásról Cantor is elismerően nyilatkozott, noha sok kritikával is élt. Frege hasonlóan állt hozzá Cantor munkáihoz. Bár a két tudós rokonszenvvel figyelte egymás munkáját, és nagyon sok hasonló gondolatmenetet fogalmaztak meg, több nagyon fontos részletben el is tértek egymástól, és végig egymástól függetlenül dolgoztak. Végül mindkettejük alkotása mint matematikai elmélet, ellentmondásosnak bizonyult. Életük végén mindketten lényegében kudarcnak könyvelték el munkásságukat, és mindketten nagyon nehezen élték meg ekkori éveiket. Ehhez hozzájárulhatott az is, hogy mindkettőjüket fájdalmas családi veszteségek érték. Végül Cantor idegszanatóriumban halt meg. Frege túljutott ezen a válságos időszakon, és lendületesen új munkába kezdett (ld. itt), de halála miatt ezt már csak elkezdeni tudta. Munkásságuk értékelése matematikai és filozófiai szempontból, illetve a nevükhöz kapcsolódó ellentmondások megoldása, sőt megoldhatósága, ma is élő probléma.
A mű tartalma[szerkesztés]
Előszó
- A jelölések magyarázata
- A tiszta gondolkodás néhány ítéletének kifejtése és levezetése
- Részletek egy általános sorozatelméletből
A Fogalomírás néhány sajátossága, újítása[szerkesztés]
- Frege a tradicionális logikában addig használt, pragmatikai és leíró nyelvtani ízű nyelv- és mondatelemzés helyett, melynek a gyökerei a szofisztikus és személyközpontú meggyőzés elméletében erednek, még ha az ezen gyökerektől való elszakadás jegyében jött is létre – ezáltal a pszichológia tudományával való rokonsága nagyobb annál a küszöbnél, amit Frege képes elviselni – egy szemantikai és a matematika tudományához sokkal közelebb álló logikai alapfogalomrendszert választ, amely a meggyőzés helyett az objektív igazság szemléletére fókuszál, az alany és állítmány, szubjektum és predikátum, szillogizmus és alakzat, és egyéb tradicionális, Frege céljainak nem megfelelő fogalmak helyett az állandó és változó, konstans és függvény, kondicionális és következtetési szabályformula fogalmaira épít,
- Bevezeti a logikai műveleteket, elsősorban a kondicionálist, ez utóbbira és a negációra visszavezetve az összes többit,
- Elmélete nem szigorú és „modern” (formalista) értelemben véve axiomatikus ugyan, mert az alaptörvényeknek nevezett axiómákat is „levezeti”, de ettől eltekintve annak mondható. Frege az általa sokat szidott formalisták elméleteitől is eltér abban, hogy minden szimbólumot nagyon alaposan körülír, értelmüket rögzíti – azaz Frege szimbólumainak, úgy az alapfogalmakat jelölőknek, mint az axiómákat leíróknak, van értelmük.
A Frege-féle logika alapelemei[szerkesztés]
Az alább leírt kételyeket is figyelembe véve, némi pontatlansággal azt mondhatjuk, Frege fogalomírása egy öt-hat alapjelből, -fogalomból álló, kilenc axiómára és két többpremisszás levezetési szabályra (modus ponens és a generalizációs szabály) alapozó, minimum elsőrendű logikai nyelv. A Frege által bevezetett jelöléseket az alábbi táblázatban foglalhatjuk össze:
Frege fogalomírásának alapjelei
Alapfogalom Frege jelölése Modern jelölés(ek) Ítélés , p(A) = 1;
p(A) = iTagadás ─┬─ , Feltételesség
(kondicionális)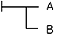
Univerzális kvantifikáció ∀y: Φ(y) Egzisztenciális kvantifikáció ∃y: Φ(y) Egyenlőség A Fogalomírásban még nem bevezetett alapjelek: Függvény (értékmenete) Deskriptor
1. táblázat
A matematikai részletekről a Frege-kalkulus c. cikkben írunk.
Állandó és változó[szerkesztés]
Frege szerint a matematikában és logikában használt jelek, ahogy az aritmetikában már szokásos volt, két csoportba kell hogy tartozzanak:
- Az egyik típusba tartozó jeleknek egy adott szövegösszefüggésben mindig ugyanazt kell jelenteniük, ezek az állandók, például 0,1,2, …, +, – , √
- A másik csoportba tartozó jelek ugyanazon szövegösszefüggésen belül is többféleképp érthetőek, ezek a változók; például az
egyenlőségben az a, b, c jelek.
Azonban egy adott szövegösszefüggésen belül ugyanazon jellel jelölt változón mindig ugyanazt kell érteni (tehát bármit behelyettesíthetünk egy változó helyére, ha attól a jelek értelmesek maradnak; de ugyanazon változó ugyanazon előfordulása helyébe mindig ugyanazt)
Megítélhető tartalmak[szerkesztés]
Azon nevek vagy jelek, melyekkel jelentésével kapcsolatban beszélhetünk az igazságról vagy hamisságról, a megítélhető tartalmakat jelölik. Azt, hogy az A jel megítélhető tartalmat képvisel, fregei jelölésmódban jelöli. A jel – mely tehát egy vízszintes vonal – neve tartalomvonal („Inhaltsstrich”).
Frege „szimbolikusan” is megkülönbözteti egy tartalom megítélhetőségét annak igazságától (tehát külön jelet is bevezet egy igaz megítélhető tartalom igazságának jelölésére). Ezt egyszerűen egy függőleges vonal jelöli, neve ítéletvonal (Urteilsstrich).
Tehát hogy A egy igaz megítélhető tartalom (igaz kijelentés), annak jele a fogalomírásban
Megjegyzés : E két jelnek, a fent leírt értelemben érve őket, nincs megfelelőjük a mai modern logikában Bővebben .
Az ítélet és fogalmi tartalom[szerkesztés]
Ugyanazt a mondatot többször is leírhatjuk. És valóban, többször is leírhatjuk ugyanazt a mondatot. Ettől a mondatot ha fizikailag nem is, de logikailag ugyanannak tekinthetjük. Sőt az olyan, logikai szempontból apró változások is lényegtelenek, mint amelyek a beszélő szándékát, elvárásait stb. jelzik egy kijelentő mondatban (és kötőszó helyet a de használata stb.). Például ez a négy mondat igazságérték és következmények szempontból ugyanaz (pontosan akkor igaz bármelyik, ha igaz bármelyik másik):
- Arkhimédesz halálakor bevették Szirakúzát.
- Hiába Arkhimédesz halála, bevették Szirakúzát.
- Arkhimédesz meghalt és Szirakúzát bevették.
- Az Arkhimédesz nevű tag bekrepált Szirakúza elfoglalásakor.
- Arkhimédesz halála Szirakúza bevételekor – tény.
Noha a mondatok jelentése köznapi szempontból egyáltalán nem ugyanaz, és maguk a mondatok sem ugyanazok, van bennük valami közös. Ezt Frege fogalmi tartalomnak nevezi. Ezt e művében nem definiálja, csak annyit mond róla, hogy a logikai szempontból „a mondatokból csak az jön számításba, ami befolyásolja annak lehetséges következményeit.”
Utóbbi mondat pontatlansága, elégtelensége miatt több furcsaság, probléma lép fel ld. itt . Későbbi műveiben (Jelentés és jelölet; A gondolat) Frege részletesen kifejti, megmagyarázza, pontosítja, hogy fogalmi tartalmon mit is ért.
Pontosan a fogalmi tartalom felismerhetősége az az ok, ami miatt Frege szerint leváltható az addig uralkodó, még Arisztotelésztől eredő tradicionális logikai szubjektum-predikátum-paradigma (ld. Arisztotelész logikája), hiszen a szubjektum (kb. „alany”) és predikátum (kb. „állítmány”) az igazságérték és következmények szempontjából általában felcserélhetőek, mivel „elképzelhető olyan nyelv, melyen az Arkhimédész életét vesztette Szirakúza bevételekor úgy is kifejezhető: Arkhimédesz erőszakos halála Szirakúza bevételekor: Tény. Az utóbbi nyelven minden, ami a mondat igazságtartalmának eldöntéséhez kell, szubjektumnak számít, predikátum pedig egyetlen van: a Tény szócska. „Ilyen nyelv a fogalomírás, és az összes ítélet közös predikátuma.”
Két jel tartalmának azonosságát, a tartalomazonosságot az jellel jelöli. Erre szükség van az aritmetikában is, például két összeg egyenlőségének kimondásakor (az aritmetikában hagyományosan az egyenlőségjelet használják: . Már a Fogalomírásban is felmerülnek ezzel a jellel és ennek jelentésével kapcsolatos problémák ld. itt, melyeket itt (1. f. 4. §.) csak érint; de későbbi műveiben még többet foglalkozik velük. A tartalomazonosság pontos definíciója a definíció:
jelöli, hogy az A és B jelek fogalmi tartalma azonos, így „az egyik bárhol helyettesíthető a másikkal” (1. f. 8. §.). Valójában ebben, a Leibniz-elvnek nevezett gondolaton alapuló definíciókísérletben rejlik a fogalmi tartalom valódi definíciója (ld. itt).
Mellesleg, az előbb említett meghatározatlanság miatt még az utóbbi definíció figyelembe vételével sem igazán egyértelmű, hogy a tartalomazonosság a fogalmi tartalmak azonosságát állítja-e ld. itt . Ez is a Jelentés és jelölet, illetve Logikai vizsgálódások (I.: A gondolat) c. későbbi művei alapján érthető meg: ezekben a jelek „fogalmi tartalmát” további részekre osztja.
A függvény[szerkesztés]
A függvény olyan kifejezésnek (jelentéssel bíró jelsorozatnak) tekinthető, melyben egy vagy több jel (az argumentumok) valamilyen változó. Például ha a "hidrogén nehezebb az oxigénnél" mondatot úgy fogjuk fel, mint a "valami nehezebb a másvalaminél" mondatban a "valami" és "másvalami" változók behelyettesítését a megfelelő gázok neveivel, akkor a "… nehezebb a …-nél" kifejezéshez mint függvényhez jutunk. Egy ilyen függvénynek több argumentuma is lehet, ha ezek például A, B, akkor ezt a alakban jelöljük. Frege „definíciója” (később írja, hogy maga sem tekinti ezt definíciónak, az ő függvényfogalma alapfogalom):
- „Ha egy kifejezésben (melynek tartalma nem feltétlenül megítélhető) egy egyszerű vagy összetett jel egy vagy több helyen előfordul, és ezt a jelet az összes vagy néhány helyen mással, azonban mindenütt ugyanazzal helyettesíthetőnek tekintjük, akkor a kifejezés változatlanul maradó részét függvénynek, a helyettesíthetőt a függvény argumentumának nevezzük.” (1. f. 9. §.)
A függvények jelölésére Frege vastag latin és görög nagybetűket használ: . Maguk a függvények is lehetnek argumentumok, ha más függvényekkel helyettesíthetőeknek gondoljuk őket: a lehet az A argumentum függvénye, de lehet a argumentumé is.
Egyik példa a Cato megölte Catót mondat, melyben három jel fordul elő. Ebből az egy kifejezésből rengeteg függvény képezhető, például az … megölte Catót kifejezés a „Cato gyilkosának lenni”, a Cato megölte …-t kifejezés a „Cato áldozatának lenni”, a … megölte …-t pedig a „valaki megölt másvalakit” függvény neve. De ha úgy gondoljuk, utóbbiban a … két előfordulása mindig ugyanazon névvel kell hogy behelyettesíthető legyen, akkor már egy másik függvény („öngyilkosnak lenni”) nevét kapjuk.
A logika és fogalomírás szempontjából legfontosabb függvények a Frege által definiált logikai függvények, az egyargumentumú tagadás és a kétargumentumú „feltételesség”.
A függvényt mint nyelvi kifejezést definiálta, de valójában ennél többről van szó. Későbbi műveiben (Függvény és fogalom) részletesebben is foglalkozik e kérdéssel, a Fogalomírásban még csak egész elnagyoltan tárgyalja.
A tagadás[szerkesztés]
A tagadás a Fogalomírás 1.f. 7. §.-e szerint:
- „Ha egy megítélhető tartalom előtti tartalomvonal alsó részén egy kis függőleges vonalat helyezünk el, ezzel azt a körülményt fejezzük ki, hogy a tartalom nem áll fenn.” Így például
azt [az ítéletet] jelenti, hogy „A nem áll fenn”. A vízszintes vonalnak a tagadásvonaltól jobbra eső része A tartalomvonala, balra eső része viszont A tagadásának tartalomvonala.
Nyomdatechnikai okokból a tagadást esetleg ¬A is jelölheti. A függőleges ítéletvonal nélküli ─┬─ A jel csak annak elgondolására szólít fel, hogy A-t tagadjuk, anélkül, hogy A állítása vagy tagadása igazságának kérdésében állást foglalnánk.
A feltételesség[szerkesztés]
A Fogalomírás 1.f. 5. §.-e szerint:
- „Ha A és B megítélhető tartalmakat jelentenek, a következő négy eset lehetséges:
| (1) | A-t állítjuk és B-t állítjuk; |
| (2) | A-t állítjuk és B-t tagadjuk; |
| (3) | A-t tagadjuk és B-t állítjuk; |
| (4) | A-tagadjuk és B-t tagadjuk. |
├────┬── A
│
└── B
|
azt az ítéletet jelenti, hogy ezek közül a harmadik lehetőség nem áll fenn, hanem a többi három közül valamelyik. Ha tehát -t tagadjuk, ez azt jelenti, hogy a harmadik lehetőség áll fenn, azaz hogy A-t tagadjuk és B-t állítjuk.”
Nyomdatechnikai okokból -t esetleg -vel is jelölhetjük a továbbiakban. Manapság az ítéletet gyakran szokás -val jelölni. Ezt a hétköznapokban úgy szokás kiolvasni, hogy „B-ből következik A”. Ez a kiovasási mód, mely Bertrand Russell nyomán eléggé elterjedt, már az ókorban is igen vitatott volt. A matematikán és általában az extenzionális elméleteken belül megengedhető (de újabban egyre kevésbé tartják szerencsésnek), azonban köznapi alkalmazása több paradoxonhoz vagy legalábbis problémához vezet. Ld. implikáció. Frege ezt a kiolvasási és interpretálási lehetőséget nem tartotta kizárólagosnak és ritkán (csak egy-két példa erejéig) alkalmazta. Az oksági kapcsolat definiálásához az univerzális kvantort is szükségesnek tartotta (1. f. 12. §.), tehát ama kapcsolat speciális esete csak az implikáció fennállása által definiált „feltételesség” kapcsolatának.
Frege műve első fejezetében megvizsgálja a három ítéletből és a feltételesség jeléből összetett egyes kijelentéseket ld. lentebb ; illetve a tagadás és feltételesség jeléből összetetteket – előáll például a alternáció vagy „(megengedő) diszjunkció” művelete, illetve nyolc másik művelet bővebben . A modern logikában számontartott logikai műveletek mindegyike formalizálható, megjeleníthető a fogalomírás segítségével, sőt mindegyik ítéletlogikai műveletre is áll ez – a Frege által bevezetett két művelet a logikai függvények egy teljes (generátor)rendszert avagy bázist alkotnak. Másképp mondva, a Fogalomírás rendszere funkcionálisan teljes. Lásd még a Frege-kalkulus c. szócikk idevágó részét.
Az általánosság[szerkesztés]
Tekintsünk valamilyen megítélhető tartalmat, azaz ítéletet. Minden ítéletben az ítélés jelétől jobbra eső jelsorozat felfogható úgy is, mint ami valamely függvény valamely argumentumába mint változóba történő behelyettesítéssel áll elő. Például a „Feri utcagyerek volt” ítélet felfogható úgy, hogy az „ … utcagyerek volt.” logikai függvény „…” argumentumába a „Feri” individuumnév helyettesítésével keletkezett.
Sokszor, de a matematikában különösen sokszor, szükség van arra, hogy egy függvény egy argumentumának minden lehetséges értékéről kijelentsük, hogy a függvény bármelyikre is alkalmazva, azaz az érték nevét a függvény adott argumentumába helyettesítve, igaz állítás adódik. Ilyenkor azt mondjuk, univerzális kvantifikációt hajtunk végre, azaz univerzálisan kvantáljuk az illető függvény illető argumentumát. Az univerzális kvantifikáció logikai operáció, melynek szimbolikus, formalizált megjelenési formája egy adott formális nyelvben az univerzális kvantor. Az így kapott ítéleteket univerzálisan kvantált mondatoknak-ítéleteknek is nevezzük. Az a függvény, melynek argumentumát kvantáltuk, hogy a mondatot kapjuk, a kvantifikáció, illetve a mondat magja (magfüggvénye). Bővebben az univerzális kvantifikáció c. szócikkben olvashatsz erről.
Frege fogalomírásában (1. f. 11. §.) így ábrázolta a függvény argumentumának univerzális kvantifikációját:
Vagyis az univerzális kvantor egy bemélyedés a tartalomvonalon, a bemélyedésbe írjuk a kvantifikálandó argumentum jelét (ez jelen esetben azaz „omega”), s mindezt úgy kell kiolvasni, hogy „minden omegára igaz nagy fí (omega) ”. Azt a változót, mely a bemélyedésben van, a kvantor hatáskörébe esőnek nevezzük. Egy változó kötött, ha kvantor hatáskörébe esik, egyébként szabad.
Modern jelölésmóddal ugyanez az univerzális kvantifikáció így fest:
Mellesleg az ítéleteket általában latin nagybetűkkel jelölte Frege; a függvényeket görög nagybetűkkel, a kvantált individuumváltozókat gót kisbetűkkel, a szabad individuumváltozókat az f,g,h betűktől különböző latin kisbetűkkel jelölte, míg az f,g,h betűket a függvényváltozók jelölésére tartotta fenn.
Az általánosság és tagadás jelével másféle kvantifikációk is elvégezhetőek, nem csak az univerzális. Az univerzális kvantifikáció tagadása Frege rendszerében is egzisztenciális állítás, mint a hagyományos logikában ( kiolvasása „Nem minden x-re …” és nem „Nincs olyan x hogy …”). Az összes arisztotelészi kvantor (kategorikus kijelentéstípus) reprezentálható:
2. táblázat
- (Modern jelölések – zárójelben a szintaktikailag Frege-hű „fordítás”)
Ugyanúgy tárgyalható az ún. logikai négyszög, ahogy a tradicionális logikában (1. f. 12. §. végén röviden meg is történik). Látható, hogy Frege rendszerében nincs értelme állító vagy tagadó ítéletről beszélni (Frege szerint ez nem logikai, hanem nyelvtani fogalom), ami a modern logikára is igaz; viszont utóbbitól eltérően Frege az univerzális és egzisztenciális kvantifikáció alapfogalomként való megkülönböztetését (és utóbbi elemi jelként való felvételét a fogalomírásba) is fölöslegesnek tartja.
A Frege-féle logika[szerkesztés]
Ezt a II. fejezetben ismerteti, „A tiszta gondolkodás néhány ítéletének kifejtése és levezetése” címen. „Tiszta” gondolkodáson természetesen nem „világost” meg „(egyedül) helyeset” kell érteni, hanem olyan gondolkodást, ami kizárólag a fogalmi tartalom sajátosságait veszi figyelembe (mai szóval ezt pontatlanul az „extenzionális” kifejezéssel írhatnánk le), de nem a nyelvtani, szubjektív vagy egyéb módon nem-logikainak tartott vonatkozásokat.
A levezetési szabályok[szerkesztés]
Két levezetési szabályt használ: a modus ponenst és a generalizációs törvényt. Ezen kívül említ még egy konvenciót, amit, lévén máshová még kevésbé sorolható, itt említünk.
- A modus ponens a következő: amennyiben érvényes és is, akkor is (tehát „ha A igaz és a-ból következik, hogy B, akkor B is igaz”).
- A behelyettesítési szabály: ha X összetett ítélet, melyben Y egy függvény argumentumának, függvénynek vagy határozatlan ítéletnek a jele (változója), akkor az Y betű minden X-beli előfordulása helyébe egy megfelelő típusú másik betűt vagy összetett kifejezést – függvény argumentumát, függvényjelet vagy ítéletjelet – helyettesítve az így kapott Z ítélet érvényes, ha X is az volt.
- A generalizációs szabály konvenciója: egy alakú kifejezésen a következőt kell érteni: . Tehát megengedhető ítéletben betű szabad előfordulása, de ez mindig univerzális kvantorral kötött előfordulást jelent (ez a konvenció egyszerűsíti az ítéletek formáját, könnyebb kiolvasást téve lehetővé).
Az axiómák[szerkesztés]
„Azon tételek száma, melyek a következő kifejtés magját képezik, kilenc. Ezek közül háromnak … a kifejtéséhez csak a feltételesség jelére van szükség, háromban … a tagadás jelét is használjuk, kettőben … a tartalomazonosság, egy formulában pedig az általánosság jelét is alkalmazzuk.” (Frege: Fogalomírás, II. f. 13. §.).
Frege kilenc axiómára alapozza a Fogalomírás rendszerét (axiómák azok az ítéletek, melyeket szemantikailag és nem szintaktikailag igazol).
Ezek a Fogalomírás számozása szerinti (1), (2), (8), (28), (31), (41), (52), (54), (58) tételek (a változókon és egyéb betűkön kívül az első háromban csak a feltételesség, a második háromban a tagadás jele is szerepel, az utánuk következő kettőben az egyenlőségjel is, végül az utolsó, kilencedik axiómában pedig az univerzális kvantifikáció). Az axiómák modern logikai átiratban (az elnevezések még a tradicionális logikából származnak, Frege csak az „modus tollens” és „duplex negatio affirmat” elnevezéseket említi):
| 1. | „bővítés előtaggal” | |
| 2. | „feltételességi lánc” | |
| 3. | „premisszakonverzió” | |
| 4. | „kontrapozíció” vagy „modus tollens” | |
| 5. | „kettős tagadás (I.)”; „duplex negatio affirmat” | |
| 6. | „kettős tagadás (II.)” | |
| 7. | „függvények egyértékűsége (egyértelműsége)” | |
| 8. | „az egyenlőség reflexivitása” | |
| 9. | „dedukció (általánosból az egyedire)” |
| 3. táblázat |
Ezeken az axiómákon Frege a generalizációs konvenció alapján másodrendű ítéleteket ért. Például
azt jelenti, úgy kell érteni,
A modern logikatankönyvek általában nem követik ezt a felfogásmódot (tekintve, hogy a másodrendű logika még csak nem is egyetemi tananyag, ez nem is igen lenne lehetséges). A legelterjedtebb modern felfogás szerint az axiómák sémák, azaz maguk nem ítéletek, csak ítéletváltozókból és logikai operátorokból álló jelsorok; melyekben a betűk helyébe megfelelő módon ítélet(nev)eket helyettesítve, igaz ítéletet kell kapnunk bármely helyettesítéssel (azaz tautologikus sémák).
A nulladrendű logika vagy ítéletkalkulus szintaktikus (más néven axiomatikus) felépítésének legismertebb módszere, a Hilbert-kalkulus, gyakorlatilag ma is a Frege által használt axiómarendszerre lentebb épül, noha hangsúlyozzuk, Frege axiómái nem nulladrendű, hanem (legalább) másodrendű logikai axiómák.
Ha Frege logikai rendszerét elsőrendűnek tekintjük (ez megfelelő szintaktikai korlátozásokkal elérhető), akkor eme korlátozott rendszert komplettnek, teljesnek nevezhetjük. Az erre vonatkozó tételt Kurt Gödel bizonyította 1930-ban (ld. az irodalomjegyzéket) ) . Eszerint ha az jól képzett (értelmes) ítéletséma nem vezethető le az elsőrendű logikában, akkor szerkeszthető hozzá „cáfoló interpretáció” (azaz olyan matematikai struktúra, melyben nem érvényes).
A Frege-axiómarendszer viszont nem független. A nulladrendű logika felépítéséhez három axióma is elegendő (az első, második és negyedik), de már Frege is javasol egyszerűsítéseket és összevonásokat műve Előszavában a formálisan elsőrendű (egyenlőségjelet vagy kvantort tartalmazó) axiómákra is.
Sorozatelmélet[szerkesztés]
A Fogalomírás III. fejezetében Frege felépít egy nagyon alapszintű sorozatelméletet (definiálja a „megelőzés”, „rákövetkezés”, „egyértelmű reláció”) fogalmakat. Frege elmélete erősen másodrendű, rengeteg, függvényekre vonatkozó kvantifikációt foglal magában (a lentebbiekben Ruzsa Imre szóhasználatát és jelöléseit alkalmazzuk, melyek eltérnek Fregéétől).
A legalapvetőbb Frege definiált reláció (a 69-es számú tétel) az öröklődés. Egy predikátumot (egyargumentumú függvényt) öröklődőnek vagy hereditáriusnak nevezünk egy relációra (kétargumentumú függvényre) nézve, ha abból a két tényből, hogy (i) előbbi egy individuumra fennáll, és (ii) utóbbi fennáll az előbbi individuum és egy másik individuum közt, következik, hogy a predikátum fennáll ama másik individuumra is. Jelekben:
.
Frege ezután definiálja a megelőzés relációját (76) egy r relációra nézve; ezzel pedig lehetőség nyílik, hogy ha adott egy r reláció, akkor annak segítségével különfle „sorozatokat” képezzünk (pontosabban, egy r meghatároz egy „sorozatot”).
Tehát a és b egymás rákövetkezői az r relációra nézve, ha minden e relációra nézve öröklődő predikátum igaz b-re, mely igaz az a-val r relációban lévő dolgokra is.
Ezután rengeteg tételt bizonyít, melyek főképp <r tranzitivitásának (98) belátásához kellenek:
.
Végül definiálja az egyértelmű (univalens) reláció fogalmát (115), és bizonyít még 11 ezzel kapcsolatos tételt:
.
Kiegészítés és megjegyzések[szerkesztés]
Az ítélés(jel)[szerkesztés]
A tartalom- és ítéletvonalnak megfelelő jelek használata a mai (extenzionális) logikában – megkérdőjelezhető módon – gyakran elsikkad; valószínűleg ennek oka az, hogy Wittgenstein Tractatusában „logikai szempontból meglehetősen értelmetlennek” minősítette (a jelet, néha használják, de mást jelöl, mégpedig egy logikai nyelven megfogalmazott matematikai elmélet egy állításának az elmélet axiómáiból való levezethetőségét; és semmiképp sem úgy fogják fel, mint két egyszerűbb jelből összetett jelet). E vélemény azonban legfeljebb az extenzionális ítéletlogika körén belül maradva tartható: már a többedrendű extenzionális logikában is fontos lehet, például míg két ítélet között a nyíl az implikáció műveletét jelöli, ami ítéletek közti művelet, és az ítéletlogikai nyelv egy állítása, mely szintén ítélet; addig azt, hogy az ítélet igaz, más jellel, leginkább az -vel szokás jelölni; ekkor viszont nem művelet az ítéletek között, hanem egy kétváltozós reláció; maga az pedig nem a logikai nyelv egy ítélete, hanem a metanyelvé (a különbség például a matematikai SH-atlaszban is összemosódik). Azon szerzők, akik mégis megkülönböztetik az ítélést az ítélettől, a jelet használják ugyanarra, amire Frege a -t. De előbbi általában már más, Frege értelmezésétől eltérő jelentést kap, az ítélet ún. szemantikus tautológia jellegét jelöli . Ráadásul ezt a jelet egészen más célokra is használják a modern logikában.
Fogalmi tartalmak és azonosságuk[szerkesztés]
A fogalmi tartalom elégtelen meghatározottsága[szerkesztés]
Utóbbi mondat pontatlansága, elégtelensége miatt is itt egy furcsaság lép fel: mivel a Frege által definiált következményreláció két mondat közti érvényessége vagy érvénytelensége csak a mondatok igazságértékétől (extenziójától) függ, eszerint a fogalmi tartalmon a puszta extenziót kell érteni? Tehát minden igaz mondat logikai szempontból ugyanaz lenne? Megjegyezzük: a modern ítéletlogika elég közel áll ehhez a felfogáshoz, minthogy e tekintetben a legradikálisabb szerzők nem is beszélnek ítéletekről, csak ítéletváltozókról; melyek az igaz vagy hamis értéket vehetik fel; az ítéletlogika pedig nem is ítéleteket vizsgál, hanem értelmetlen formulákat.
További probléma az, hogy ha a „fogalmi tartalom” kifejezést nemcsak mondatokra, hanem másféle logikai jelekre is vonatkoztatjuk, mond-e valamit a fenti mondat az utóbbi féle jelek fogalmi tartalmáról? Későbbi műveiben (Jelentés és jelölet; A gondolat) Frege részletesen kifejti, megmagyarázza, pontosítja, hogy fogalmi tartalmon mit is ért.
A tartalomegyenlőség(jel)[szerkesztés]
A tartalomazonosság és jele kapcsán felmerül a kérdés, hogy az , ill. fregei jellel az jel mint reláció milyen fajta relációnak a megjelenítése: olyané, amely tartalmak között hat, vagy olyané, amely a jelek között? Azért érdekes kérdés ez, mivel bármelyik választ is adjuk, mindkettő tekinthető paradoxnak egy bizonyos szemszögből.
Frege (ma már elég kézenfekvőnek tartott) válasza, hogy = a jelek közötti reláció (1. f. 8. §.).
- Ha ugyanis = tartalmakra vonatkozó reláció lenne, akkor különböző tartalmak közé kitéve, mindig hamis állítást kapnánk. Csakis akkor kaphatnánk igaz állítást, ha ugyanaz állna az egyenlőség két oldalán. Tehát például 1+3 = 2+2 esetén az 1+3 és 2+2 jelek tartalma különböző kellene hogy legyen; de hiszen nem így van, különben 1+3 ≠ 2+2 lenne, és ezt hamis állításnak tudjuk. Így értve, az = jelet semmilyen más esetben nem alkalmazhatnánk, mint az A = A alakú állítások leírására, tehát az = jel elég fölösleges dolog lenne. A=B ugyanazt fejezné ki, mint a triviális A=A állítás.
- Viszont ha = jelek közti reláció, akkor is látszólag fölösleges, hiszen ha az A és B jelek ugyanazt fejezik ki, akkor nyugodtan törölhetjük a B jelet a nyelvből, mint fölösleges redundanciát, az A=B jelnek ez esetben sincs információtartalma. Ugyebár egy ideális nyelvben teljesen fölösleges két jel egyazon dologra? Tehát bármelyik álláspontot is fogadjuk el az = jelentésével kapcsolatban, mindenképp fölösleges ez a jel? Frege azzal a teljesen nyilvánvaló dologgal érvel, hogy ez nem így van. Ha például egy jel valami összetett állítást fejez ki, akkor sokszor éppen az a tudományos munka, hogy bebizonyítsuk, jelentése ugyanaz, mint egy másik jelé. Mint egy másik művében írja:
- „Az, hogy minden reggel új Nap kel fel, alighanem egyike volt a csillagászat legtermékenyebb felfedezéseinek. Egy [más-más névvel jelölt, de valójában ugyanazon] kisebb bolygó vagy üstökös azonosítása azonban ma sem mindig magától értetődő … Az Alkonycsillag a Nap által megvilágított égitest mondatban más a gondolat, mint ebben: A Hajnalcsillag a Nap által megvilágított égitest. Olyan valaki, aki nem tudja, hogy az Alkonycsillag azonos a Hajnalcsillaggal, az egyik gondolatot igaznak, míg a másikat hamsinak tarthatja.” (Jelentés és jelölet, 1. old.)
Ez vezet a fent említett Jelentés és jelölet c. munkájában a jel háromdimenziós modelljének megalkotásához, mely modell alapján megalapozható az a vélemény, hogy az = jelnek van tartalma, és eme tartalom bizonyos értelemben megfoghatóvá is válik.
Mellesleg, az előbb említett meghatározatlanság miatt még az utóbbi definíció figyelembe vételével sem igazán egyértelmű, hogy a tartalomazonosság a fogalmi tartalmak azonosságát állítja-e. Ez is a Jelentés és jelölet, illetve Logikai vizsgálódások (I.: A gondolat) c. későbbi művei alapján érthető meg: a jel fogalmi tartalmát kettéválasztja az extenzionális jellegű jelöletre, pontosan ez az, ami pontosan és kizárólag befolyásolja a logikai törvények szerint meghatározta, a következményeket és igazságértékeket befolyásoló viselkedést, és az intenzionális jellegű jelentésre, ami viszont a mondatok esetében a mondat jelentésének (a gondolatnak) az objektivitását, de az összes azonos extenziójú mondatok közti különbségtétel lehetőségét is, biztosítja.
A „láncformula”[szerkesztés]
A feltételesség jeléből és hasonló építőelemekből (a fogalomírás mint nyelv betűiből/szavaiból) már sok mindent lehet építeni.
Ilyen például a
├────┬────── A
│
└──┬─── B
│
└─── C
|
formula, mai jelöléssel ezt vagy formában írnánk. Ez (és általában ezek a fajta, „balrekurzív” formulák, melyek előtagja is implikációs formula) viszonylag csekély fontosságú.
Fontosabbak azok a „jobbrekurzív” implikációs formulák (melyek utótagja is implikáció), melyeknek legegyszerűbb képviselője, nevezzük láncformulának (Frege nem ad neki külön nevet),
├──┬───┬─── A │ │ │ └─── B │ └─────── C |
Ezt modern jelöléssel egyébként alakba írhatnánk. A formula szerepéről itt olvasható bővebben.
Logikai műveletek a Fogalomírásban[szerkesztés]
Frege az 1. f. 7. §.-ban kimutatja, hogy a tradicionális logikában használt logikai műveletek (melyeket az „és”, „vagy”, „sem-sem” .. stb. ) kötőszavak reprezentálnak a köznyelvben, kifejezhetőek fogalomírása segítségével. Ez pusztán a tagadás és a feltételesség jelének kombinációit felírva megtehető.
Sorra véve, hogy két A, B ítélet, a tagadás és a feltételesség jeléből összekombinálva milyen logikai függvények kaphatóak, azt tapasztaljuk, hogy az összes fontos (a modern logika által számontartott) kétváltozós logikai művelet előáll Frege rendszerében (ld. még a a Frege-kalkulus c. cikket is):
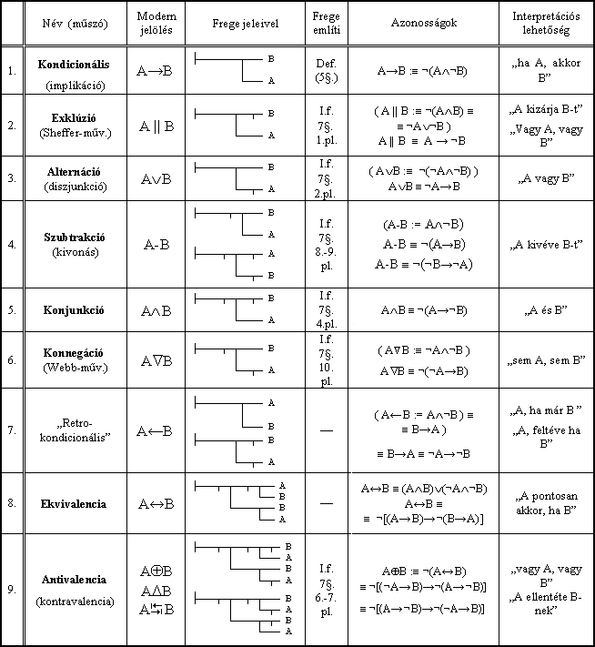
Az alternáció és konjunkció előállítása[szerkesztés]
Például egyszerűen látható, hogy a „megengedő vagy”, azaz alternáció (vagy diszjunkció) művelete hogyan fejezhető ki. Mivel
├────┬───── A
│
└───── B
|
„tagadja azt az esetet, amikor B-t állítjuk és A-t tagadjuk”, ezért ennek állítása azt jelenti, hogy B-t nem állítjuk, vagy pedig A-t nem tagadjuk. Azaz hogy B-t tagadjuk és A-t állítjuk. Ezért
├────┬───── A
│
└───┬─ B
|
tagadja, hogy B tagadását állítjuk és A-t tagadjuk, azaz azt, hogy B-t és A-t is tagadjuk, tehát B-t nem tagadjuk vagy A-t nem tagadjuk. Ez tehát azt jelenti, hogy A-t állítjuk, vagy B-t. Ez tehát a „vagy” kötőszóval leírt diszjunkció. Mai jelölésekkel elmondva, .
Lásd még a Frege-kalkulus c. cikket témába vágó részét.
Az -vel jelölt „és” művelet, a konjunkció is előállítható a fogalomírásban (7. §. 4. példa):
├───┬─┬───┬─ A
│
└───── B
|
Azaz; .
Frege példái[szerkesztés]
Az áttekinthetőség kedvéért foglaljuk össze, hogy az 1. f. 7. §.-ban Frege mely példákat veszi sorra (nyomdatechnikai okok miatt modern jelölésben közöljük):
- , ma exklúzió, Sheffer-művelet;
- , ma alternáció (diszjunkció); emellett beszél a „vagy” kötőszó kizáró (diszjunktív) használatáról, de csak az 5.-6. példa alatt formalizálja;
- , ma (háromváltozós) alternáció;
- , ma konjunkció;
- , ma (háromváltozós) konjunkció.
- , ma antivalencia (kontravalencia);
- , ami szintén az antivalencia egy lehetséges formalizálása a fogalomírásban;
- , az művelet;
- , ugyanaz mint az előbbi;
- , ma a Webb-féle „sem-sem” (konnegáció) művelet.
Összehasonlítás más elméletekkel[szerkesztés]
Arisztotelészi logika és arisztoteliánus logika[szerkesztés]
Frege legnagyobb újításai közül az elsőként említendő a retorikus-szinkopált metanyelvről a szimbolikus logikára való áttérés. A Fogalomírás nyelve legalább másodrendű. Fregénél az arisztotelészi, nyelvi-metafizikai-lételméleti alapú, a lényeg fogalmára alapozott nevek és terminusok helyett inkább ismeretelméleti alapú, a függvény fogalmára alapozott fogalmak szerepelnek. Frege az arisztotelészi és tradicionális szintaktika rengeteg elemét (általános és különös, állító és tagadó, hipotetikus és diszjunktív, modális) pragmatikai eredetűnek gondolja, nem utasítja el őket mint logikai kategóriákat, de száműzi a maga extenzionális rendszeréből és szintaktikájából (az 1. f. 4. §-ében).
A Boole–Schröder-algebra[szerkesztés]
George Boole, a matematikai logika másik atyja inkább (rendűség nélküli) osztálylogikát művelt, nem pedig elsőrendű predikátumlogikát. Ennek megfelelően művei nyelvezete, szimbolikája is teljesen más, habár a tradicionális logika nagy részét, például a kvantorokat és kategorikus ítéleteket, ő maga is rekonstruálni tudja saját rendszerében. Érdeklődése is teljesen más, kevésbé a következtetések (a művelet, implikáció), mint inkább az osztályok algebrájának (a logikai műveletek osztályelméleti megfelelői) törvényei érdeklik; a matematika megalapozása a logika segítségével pedig még kevésbé (inkább fordítva).
A Hilbert-kalkulus[szerkesztés]
A nulladrendű logika Hilbert-kalkulusa Frege elméletének egy korlátozásának tekinthető. Három axiómára épül:
Általában az utolsó axióma helyett a következőt használják („reductio ad absurdum”-axióma), ez is több ekvivalens változatban fordulhat elő (de az így kapott rendszer „ugyanaz”, mint a fent leírt, ugyanazokat lehet levezetni belőle is):
3A).
Levezetési szabály a modus ponens.
Magyarul[szerkesztés]
- Logika, szemantika, matematika. Válogatott tanulmányok; ford. Máté András, szerk., jegyz., bev., tan. Ruzsa Imre; Gondolat, Bp., 1980
- Logikai vizsgálódások. Válogatott tanulmányok; ford. Máté András, Bimbó Katalin, jegyz., bev. Ruzsa Imre; Osiris, Bp., 2000 (Osiris könyvtár. Tertium non datur)
Hivatkozások[szerkesztés]
Jegyzetek[szerkesztés]
- ↑ Ami a cím első szavát (Begriffsschrift) illeti, ezt a 19. században a német nyelvben használták időnként az egyiptomi hieroglif írás (ill. hasonló írásrendszerek, pl. a kínai írás) logogrammatikus jellegének kidomborítására. Ld. pl. Konrad Hermann: Das Problem der Sprache und seine Entwickelung in der Geschichte (Drezda, R. Kuncze kiadása, 1865; 21. f. (Die sprache und die Begriffsschrift; 66. o. - ), ld. még K. F. Merleker: Musologie (F. Brockhaus, 1857, 7. old.). Nincs különösebb bizonyítéka, hogy Frege gondolt volna erre az értelmezésre a címadáskor.
Kapcsolódó szócikkek[szerkesztés]
Irodalom[szerkesztés]
(forrásul szolgáló, illetve további művek)
- Frege, Gottlob (szerk. Ruzsa Imre): Logika, szemantika, matematika. Fordította Máté András. Gondolat, 1980. ISBN 963-280-795-2.
- Gödel, Kurt: Die Vollständigkeit der Axiome des logischen Funktionenkalküls. Monatshefte für Mathematik und Physic, 37, (349.-360. o.), 1930.
- Hersh, Reuben: A matematika természete (What is mathematics really?). Typotex Kiadó, 2000. ISBN 963-9132-57-8.
Recenziók a Fogalomírásról[szerkesztés]
- T. W. Bynum: Gottlob Frege, Conceptual Notation and Related Articles (Oxford: Clarendon, 1972. Appendix I.) – a hat korabeli recenziót összegyűjtve tartalmazza.
További információk[szerkesztés]
- A Fogalomírás német eredetiben (laponkénti PDF-képek)
- A Fogalomírás tételei modern jelölésmódban (R. Mendelsohn) Archiválva 2005. május 3-i dátummal a Wayback Machine-ben PDF, angolul
- Farkas János László: Szabad szemmel górcső alatt (adalékok Frege és a Fogalomírás filozófiájához)
- A Begriffsschrift részletesen vázlatos leírása (angolul)
- Rövid leírás (angol), fénykép a Fogalomírásról
- Frege (és mások) koncepciója a logikáról (Øystein Linnebo) (PDF) (angolul)
- Tanulmány a Fogalomírásról és a modern logikáról (Richard Mendelsohn) Archiválva 2005. május 3-i dátummal a Wayback Machine-ben (PDF) (angolul)
- Jeff Speaks írása (PDF) (angolul)
- Nyelvfilozófia, logika
- Neologicista linkek



































![{\displaystyle \vdash \ \ \left[\ A\rightarrow \left(B\rightarrow C\right)\ \right]\ \rightarrow \ \left[\ \left(A\rightarrow B\right)\rightarrow \left(A\rightarrow C\right)\ \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46233b0b84387b488948fe5ad59cef954c68fc83)
![{\displaystyle \vdash \ \ \left[\ D\rightarrow \left(B\rightarrow A\right)\ \right]\ \rightarrow \ \left[\ B\rightarrow \left(D\rightarrow A\right)\ \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fdf8f5830ad951a8c528ea7eec78a90a79a61594)






![{\displaystyle Her\left(\ P(.)\ ,\ r(.,.)\ \right)\ :=\ \forall x:\ \left(\ P(x)\rightarrow \forall y:\left[\ r(x,y)\rightarrow P(y)\ \right]\ \right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48a42dc31befe1657b5fa087832a5cfacc6316f0)
![{\displaystyle a<_{r}b\ :=\ \forall P:\left(\ \ Her(P,r)\rightarrow \left(\ \forall x:\ \left[r(a,x)\rightarrow P(x)\right]\rightarrow P(b)\ \right)\ \right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f6f1f490a614872b3d42b2dab0fb311596562d2)
![{\displaystyle \vdash \ \left[\ x<_{r}y\ \rightarrow \ \left(\ y<_{r}z\ \rightarrow \ x<_{r}z\ \right)\ \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e5b3e63e3dae31c12923f4d3fd8ddddce32107b)
![{\displaystyle \vdash \ Un(r(.,.)):=\forall x\forall y:\ f(x,y)\rightarrow \left(\forall z:\ \left[f(x,z)\rightarrow (y=z)\right]\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7bce2c96234a541b95f1900a08e6462224bac678)































![{\displaystyle \left(\lnot A\rightarrow B\right)\rightarrow \left[\left(\lnot A\rightarrow \lnot B\right)\rightarrow B\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db83adcf3c9c67a4aecd50cc28943c5d5b120adb)