Lineáris leképezés
Egy lineáris leképezés (vagy lineáris operátor) a matematikában, közelebbről a lineáris algebrában, egy azonos test feletti vektorterek között ható művelettartó függvény (szakszóval vektortér-homomorfizmus). Egy operátor bemenete tehát vektor, kimenete pedig szintén vektor, az úgy nevezett képvektor. Lineáris tehát egy ilyen vektorhoz vektort rendelő leképezés, ha
- két vektor összegének képe a két vektor képének összege, és
- egy vektor számszorosának képe a vektor képének ugyanezen számszorosa.
Leggyakrabban a valós, a komplex test vagy a kvaterniók feletti operátorokról van szó.
A geometria szempontjából a térbeli lineáris leképezések olyan affin leképezések, melyeknek van fixpontja. Algebrai szempontból a lineáris leképezés egy vektortér-homomorfizmus. A kategóriaelméletben a vektorterek kategóriájában az objektumok közti morfizmus. Az analízisben szintén vannak alkalmazásai, hiszen a Hilbert-terek közt ható függvények is lineáris operátorok.
Definíciók[szerkesztés]
Legyen V és U a test feletti két vektortér. Az leképezést lineárisnak nevezzük, ha minden v1 és v2 ∈ V vektorra, illetve minden λ ∈ elemre és v ∈ V vektorra egyszerre rendelkezik az alábbi két tulajdonsággal:
- additivitás:
A fenti definíció egyenértékű azzal, hogy megtartja a lineáris kombinációképzést, azaz bármely n természetes szám esetén minden λ1, λ2, … , λn -beli elemre és v1, v2, … , vn ∈ V vektorra:
- .
Ha V és U megegyezik, akkor lineáris transzformációról beszélünk.
Ha ki akarjuk hangsúlyozni (például az egyértelműség kedvéért), hogy egy feletti lineáris leképezés, akkor azt mondjuk, hogy az leképezés -lineáris. Különleges esetben ennek jelentősége lehet, például a , konjugálás ugyan -lineáris, de nem -lineáris.
A típusú lineáris leképezéseket (a vektortérből az alaptestbe mint egydimenziós vektortérbe képező lineáris leképezéseket) lineáris funkcionáloknak nevezzük. Például a duális tér elemei lineáris funkcionálok.
A lineáris leképezés rangja a képterének dimenziója, azaz
- módon definiált képtér esetén
- .
Magyarázat[szerkesztés]
Egy leképezés lineáris, ha megőrzi a vektortér szerkezetét, vagyis az összeadást és a skalárral szorzást. Legyenek vektorok a vektortérben! Ekkor, ha , akkor , így az összegzés átvihető az értékkészletre:
A következtetés egyszerűsíthető, ha elvégezzük a behelyettesítését az összegbe: . Hasonlóan írható le a skalárral szorzás is. Ez teljesül, hogyha követi és kapcsolatát, vagyis az értékkészletben is fennáll:
Elvégezve a helyettesítését az következménybe kapjuk, hogy .
-
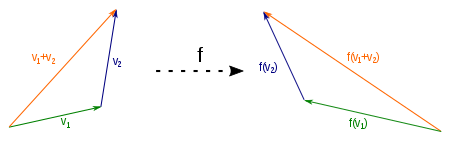
A vektorok összeadásának megőrzésének bemutatása: Minden , és által megadott addíciós háromszöget megőriz az lineáris leképezés. Az , és vektorok is addíciós háromszöget alkotnak és teljesül, hogy .
-
Az összeadást nem megőprző leképezéseknél vannak , és vektorok úgy, hogy , és nem alkot addíciós háromszöget, mivel . Egy ilyen leképezés nem lineáris.
-
A skalárral szorzás megőrzésének bemutatása: Minden skálázást megőriz a lineáris leképezés, és teljesül, hogy .
-
Ha egy leképezés nem őrzi meg a skalárral szorzást, akkor van egy skalár és egy vektor úgy, hogy a skálázás nem a skálázásra képeződik. Egy ilyen leképezés nem lineáris.
Jelölése[szerkesztés]
Szokás az operátorokat írott betűvel jelölni, vagy kettővel aláhúzni, vagy cirkumflexet tenni fölé, vagy görög betűvel jelölni, vagy az argumentuma köré nem tenni zárójelet:
- , , , ,,
Fajtái[szerkesztés]
- Monomorfizmus: injektív lineáris homomorfizmus
- Epimorfizmus: szürjektív lineáris homomorfizmus
- Izomorfizmus: bijektív lineáris homomorfizmus
- Endomorfizmus: lineáris homomorfizmus
- Automorfizmus: bijektív lineáris homomorfizmus
Mag és kép[szerkesztés]
A mag és a kép lineáris leképezések szempontjából fontos vektorterek. Legyen lineáris leképezés! Ekkor:
- Az kép az szerinti képvektorok halmaza, azaz azokat és csak azokat a vektorokat tartalmazza, melyek előállnak, mint , ahol . Úgy is jelzik, mint . Ez a halmaz a altere. Úgy is nevezik, hogy képtere.
- A mag azoknak a -beli vektoroknak a halmaza, azaz azokat és csak azokat a vektorokat tartalmazza, melyek nullvektorára képeződnek le. Ez a mag altér -ben. Az leképezés pontosan akkor injektív, ha csak a nullvektort tartalmazza. Úgy is nevezik, mint magtere.
Tulajdonságai[szerkesztés]
- Minden lineáris leképezés esetében az U-beli neutrális elem (ami vektorterek esetében a nullvektor) képe a V-beli neutrális elem, azaz ha , akkor . Ha U és V megegyezik, akkor a neutrális elem az adott lineáris transzformáció fixpontja.
- Egy lineáris leképezés esetén a mag és a kép kapcsolatát a homomorfiatétel írja le: a faktortér izomorf a képpel.
Mátrixreprezentáció[szerkesztés]
Véges dimenziós vektorterek közötti lineáris leképezések mátrixleképezésekkel reprezentálhatók, de a lineáris leképezéshez tartozó mátrix függ a vektortér általunk választott bázisától. A mátrixleképezés olyan függvény, amely egy rögzített A m×n-es mátrix mellett bármely v n-elemű vektorhoz az A·v m-elemű vektort rendeli.
Ugyanakkor lineáris leképezésekről akkor is beszélhetünk, amikor a leképezésnek nincs mátrixa (pl. végtelen dimenziós vektorterek esetében).
Előírhatósági tétel[szerkesztés]
Ha és két V U véges dimenziós vektorterek között ható lineáris leképezés, (b1, b2, …, bn) bázis V-ben, és mindkét leképezés a bázis elemein ugyanazt veszik fel, azaz
akkor a két leképezés azonosan egyértelmű, azaz .
Ez a lineáris leképezések előírhatósági tétele. Eszerint egy lineáris leképezést, ha n dimenziós térből képez egy véges térbe, a véges tér n darab vektora egyértelműen meghatározza.
Leképezés mátrixa[szerkesztés]
Az előírhatósági tétel értelmében rögzített bázis (a kiindulási és az érkezési térben rögzített bázispár) esetén a lineáris leképezést egyértelműen meghatározza a V bázisát alkotó vektorok képeinek koordinátamátrixa, melyen a következő m×n-es mátrixot értjük:
ahol B = (b1, b2, …, bn) a V bázisa, C az U bázisa, a mátrix oszlopai pedig a B elemeinek általi képvektorai mint m-elemű oszlopvektorok. Ha az U tér m-dimenziós, akkor a mátrix összesen m n darab (szám)adatot tartalmaz. Ha típusú, akkor csak -t szokás írni, ami a vektortér-dimenziók azonossága miatt egy négyzetes mátrix lesz. Ha pedig pusztán -t írnak, akkor az azt jelenti, hogy a n-dimenziós vektortér (például ) bázisaként az (ahol i = 1, 2, ... , n) vektorok alkotta természetes avagy sztenderd bázisról van szó, azaz a
vektorrendszerről.
A bázisok ilyetén jelölése mellett a képvektorok koordinátáit a következő egyszerű mátrixszorzással számíthatjuk ki:
Hasonló mátrixok[szerkesztés]
Egy lineáris leképezéshez a vektorterek általunk választott különféle bázisai esetében más-más mátrix tartozik. Az azonos lineáris leképezéshez tartozó különféle mátrixok közötti algebrai kapcsolatot az alábbi tétel adja meg.
Definiáljuk először a hasonlóság tulajdonságát: egy A n×n-es négyzetes mátrix hasonló egy B mátrixhoz (jelölésben: A ∼ B), ha létezik olyan invertálható P mátrix, amelyre
- .
Bizonyítható állítások:
- Két mátrix pontosan akkor hasonló, ha van két olyan bázis, amelyekben a mátrixok ugyanazon lineáris leképezéshez tartozó mátrixok.
- A hasonló mátrixok karakterisztikus polinomjai megegyeznek, és emiatt sajátértékeik is azonosak.
- Egy lineáris leképezés rangja megegyezik a bármely bázis választása esetén hozzá tartozó mátrix rangjával. Ebből következik, hogy hasonló mátrixok rangjai megegyeznek.
Lineáris leképezések tere[szerkesztés]
Az azonos test feletti, V-ből U-ba képező lineáris leképezések vektorteret alkotnak a pontonként összeadással és skalárszorzással. Ezt a vektorteret általában Hom(V, U)-val vagy Lin(V, U)-val jelölik, ahol a „Hom” rövidítés nyilván a vektortér-homomorfizmusra utal.
A Hom(V, V) vektortér elemei (azaz a V V vektortér-automorfizmusok) ezen kívül egységelemes algebrát alkotnak a kompozíció műveletével mint szorzással.
A V V lineáris bijekciók invertálhatóak is. A kompozícióval mint művelettel egy csoportot alkotnak, a V-feletti általános lineáris csoportot (GL(V)).
Operátorműveletek és mátrixműveletek[szerkesztés]
A lineáris leképezésekkel végezendő műveletek véges dimenziós vektorterek és rögzített bázisok esetén megfeleltethetők mátrixokkal végzendő műveleteknek:
- Összeadás
- Skalárszorzás
ahol a [.] mindenütt az adott leképezés mátrixreprezentációját jelöli.
Dimenziótétel[szerkesztés]
A dimenziótétel kimondja, hogy a -t -be képező lineáris leképezés magjának és képének dimenziójának összege megegyezik
Példák[szerkesztés]
esetén a lineáris leképezések alakja , ahol .
Ha nyílt intervallum, az intervallumon folytonosan differenciálható valós értékű függvények vektortere, és az intervallumon folytonos valós értékű függvények tere! Ekkor
, ,
vagyis a deriválás lineáris leképezés. Hasonlóak teljesülnek más lineáris differenciáloperátorokra.
Síkbeli lineáris transzformációk és felett a természetes bázishoz tartozó mátrixaik:
- identitás
- forgatás az origó körül
- 90 fokkal az óramutató járásával ellentétes irányban:
- tetszőleges θ szöggel az óramutató járásával ellentétes irányban:
- 90 fokkal az óramutató járásával ellentétes irányban:
- tükrözés
- az x-tengelyre:
- az y-tengelyre:
- az x-tengelyre:
- kétszeres nagyítás:
- vízszintes nyírás:
- hiperbolikus forgatás:
- merőleges vetítés az x-tengelyre:
- merőleges vetítés az y-tengelyre:
Nem lineáris transzformáció:
- eltolás (de előállítható eggyel magasabb dimenzióban lineáris leképezésként, fixpont helyett fixegyenessel)
-
Az transzformáció lineáris leképezés, ami koordinátát a -szeresére nyújtja.
-
Ez a leképezés additív: Mindegy, hogy előbb összeadjuk-e a vektorokat és utána képezzük le, vagy először leképezzük és utána adjuk össze őket: .
-
Ez a leképezés homogén: Mindegy, hogy először a vektort skálázzuk és utána képezzük le, vagy pedig először leképezzük a vektort és utána skálázzuk: .
Véges terek közötti lineáris leképezések[szerkesztés]
Bázis[szerkesztés]
Egy lineáris leképezést egy bázis vektorainak képe egyértelműen meghatározza. Legyenek bázis -ben, és legyenek vektorok -ben! Ekkor pontosan egy lineáris leképezés van, ami -et -re, -t -re, …, -t -re képéezi. Ha tetszőleges vektor -ben, akkor egyértelműen előáll a bázisvektorok lineáris kombinációjaként:
Itt a vektor koordinátái a bázisban. Képvektora, előáll, mint
Az leképezés pontosan akkor injektív, ha a vektorok lineárisan függetlenek. Pontosan akkor szürjektív, ha generátorrendszer -ben.
Ha a minden eleméhez tetszőleges vektorokat rendelünk -ből, akkor a fenti képlettel egyértelműen kiterjeszthető lineáris leképezéssé.
Ha a vektorok bázist alkotnak -ben, akkor ezzel megalkotható a lineáris leképezés mátrixa a két bázisra vonatkozóan.
Mátrixábrázolás[szerkesztés]
Ha és véges dimenziós vektorterek, , , és bázisa -nek, illetve bázisa -nek. Ekkor minden lineáris leképezés ábrázolható -es mátrixként. Ez megkapható a következő módon:
A bázis minden bázisvektorához hozzárendelt vektort előállítjuk a bázisvektorok lineáris kombinációjaként:
Az , , koordináták az mátrix komponensei:
A -edik oszlop tartalmazza koordinátáit a bázisban.
Ezzel a mátrixszal minden vektor képvektora kiszámítható:
Az képvektor koordinátáira vonatkozóan szintén teljesül -re vonatkozóan, hogy .
Ez kifejezhető mátrixszorzásként:
Az mátrix az leképezés mátrixa. Az mátrix más írásmódjai: és .
Végtelen dimenziós vektorterek közötti leképezések[szerkesztés]
A funkcionális analízis keretében a végtelen dimenziós vektorterekben a lineáris leképezéseket lineáris operátoroknak nevezik. Többnyire teljes normált terek közötti leképezéseket vizsgálnak; ezek Banach-terek. Mivel a Baire-féle kategóriatétel szerint az efféle tereknek nincs megszámlálható bázisa, azért nem elég a leképezéseket egy bázison keresztül tanulmányozni. Hogy egyáltalán létezik valamilyen bázis, azt csak a kiválasztási axióma biztosítja. Ehelyett más bázisfogalmat használnak, mint az ortonormált bázis vagy az általánosabb Schauder-bázis. Így bizonyos operátorok, mint a Hilbert-Schmidt-operátorok ábrázolhatók végtelen mátrixokkal, és végtelen lineáris kombinációkkal.
A lineáris leképezések vektortere[szerkesztés]
Legyenek és a test fölötti vektorterek! Ekkor használják a vagy az jelölést a lineáris leképezéseinek -be menő halmazára. Ez szintén vektortér a test fölött, ami a -ből -be menő leképezések altere.
Ez azt jelenti, hogyha és lineáris leképezések, akkor összegük szintén lineáris leképezés:
és egy lineáris leképezés skalárszorosa is lineáris leképezés:
ahol .
Ha dimenziója , és dimenziója , illetve adva van -ben egy bázis, és -ben egy bázis, akkor az
leképezés izomorfizmus a mátrixtérben. Az vektortér dimenziója .
Speciálisan, ha , akkor a lineáris leképezések egymás utáni elvégzéssel szorozhatók is, amivel asszociatív algebrát alkotnak, amelyet jelöl.
Általánosítás[szerkesztés]
Egy lineáris leképezés egy speciális affin leképezés.
Ha test helyett gyűrű fölött vizsgálódunk, akkor modulhomomofizmust kapunk.
Források[szerkesztés]
- PlanetMath: Linear transformation Archiválva 2007. szeptember 30-i dátummal a Wayback Machine-ben
- Encyclopaedia of Mathematics: Linear operator
- MathWorld: Linear Transformation
- Albrecht Beutelspacher: Lineare Algebra. Eine Einführung in die Wissenschaft der Vektoren, Abbildungen und Matrizen. 6., durchgesehene und ergänzte Auflage. Vieweg Braunschweig u. a. 2003, ISBN 3-528-56508-X, S. 124–143.
- Günter Gramlich: Lineare Algebra. Eine Einführung für Ingenieure. Fachbuchverlag Leipzig im Carl-Hanser-Verlag, München 2003, ISBN 3-446-22122-0.
- Detlef Wille: Repetitorium der Linearen Algebra. Band 1. 4. Auflage, Nachdruck. Binomi, Springe 2003, ISBN 3-923923-40-6.
Fordítás[szerkesztés]
Ez a szócikk részben vagy egészben a Lineare Abbildung című német Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.



























































![{\displaystyle [{\mathcal {A}}]_{B,C}={\begin{bmatrix}{\begin{matrix}\vert \\\vert \\{\mathcal {A}}\mathbf {b} _{1}\\\vert \\\vert \end{matrix}}&{\begin{matrix}\vert \\\vert \\{\mathcal {A}}\mathbf {b} _{2}\\\vert \\\vert \end{matrix}}&...&{\begin{matrix}\vert \\\vert \\{\mathcal {A}}\mathbf {b} _{n}\\\vert \\\vert \end{matrix}}\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a959084bbd617b5ccce18df65fcac1ed7a0b603)
![{\displaystyle [{\mathcal {A}}]_{B,C}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2cfee7e04ffa46629993d78fd3ae600fbb30f740)


![{\displaystyle [{\mathcal {A}}]_{B}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04fd4c60c37a9464e2456df28bb802ca9bfe0fa3)
![{\displaystyle [{\mathcal {A}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c8d16dd600188d1cd571b8483155ac3449dee5c)




![{\displaystyle [{\mathcal {A}}\mathbf {v} ]_{C}=[{\mathcal {A}}]_{B,C}\cdot [\mathbf {v} ]_{B}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb2f82a43048966e387a6c4964930ede514036b9)

![{\displaystyle [{\mathcal {A}}\circ {\mathcal {B}}]=[{\mathcal {A}}]\cdot [{\mathcal {B}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ef83903a30bf48bd284b294861a3c440b170d5a)
![{\displaystyle [{\mathcal {A}}^{-1}]=[{\mathcal {A}}]^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b70971e6440b304033209df79d138e52068b8904)
![{\displaystyle [{\mathcal {A}}+{\mathcal {B}}]=[{\mathcal {A}}]+[{\mathcal {B}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8606d7db4e7349676df77f62b182f5857ec74d31)
![{\displaystyle [\lambda {\mathcal {A}}]=\lambda \cdot [{\mathcal {A}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e723554a65206c10ff55ab10c7f53c8b958c2d0b)

































































![{\displaystyle _{B'}[f]_{B}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/062cd3a0f31d7327c7da18cc418a016a9c4a0279)














