Kvaterniók

Hamilton

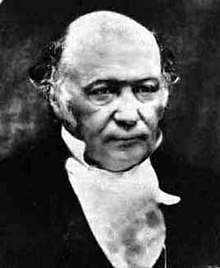
A matematikában a kvaterniók a komplex számok négy dimenzióra történő nem kommutatív kiterjesztései. Először Sir William Rowan Hamilton ír matematikus, fizikus és csillagász vezette be 1843-ban (Hamilton-féle számoknak is nevezik).

Definíció

Csoportelméleti definíció

Hasonlóan ahhoz, ahogy a komplex számokat a valós számkör i-vel való kiegészítésével kaptuk, ahol i kielégíti az i² = −1 egyenlőséget, a kvaterniókat az i, j és k elemeknek a valós számkörhöz való hozzávételével nyerjük, ahol i, j és k teljesíti a következőket:

$i^{2}=j^{2}=k^{2}=ijk=-1.\,$

Ha a szorzást asszociatívnak tekintjük (és valóban az is), a következő egyenlőségek állnak fenn:

${\begin{matrix}ij&=&k,&&&&ji&=&-k,\\jk&=&i,&&&&kj&=&-i,\\ki&=&j,&&&&ik&=&-j.\end{matrix}}$

Minden kvaternió felírható a báziskvaterniók (1, i, j és k) lineáris kombinációjaként, azaz minden kvaternió egyértelműen kifejezhető a + bi + cj + dk alakban, ahol a, b, c és d valós számok.

Halmazelméleti definíció

$\mathbb {H}$=$\{$(a, b, c, d) $\in \mathbb {R}$⁴$\}$

Halmazelméleti szempontból a kvaterniók a komplex számok önmagukkal vett direktszorzataként értelmezhetők, a következő összeadási és szorzási szabályokkal:

• (a, b, c, d)+(A, B, C, D) = (a+A, b+B, c+C, d+D)
• Szorzásukat egyszerűbb kifejezni az alábbi jelölésekkel: (a, b, c, d) = (a, v), ahol a egy valós szám, v egy háromdimenziós vektor, valamint v*V a skaláris szorzatukat, v x V pedig a vektoriális szorzatukat jelöli. Ekkor (a, v) * (A, V) = (a*A-v*V, a*V + A*v + v x V)

A kvaterniók ferdetestet alkotnak.

Komplex mátrixok

Ez a konstrukció a kvaterniókat részgyűrűnek tekinti a ${\mathbb {C}}^{2\times 2}$-es mátrixok gyűrűjében. Az 1, i, j, k báziskvaterniókat ezek a mátrixok ábrázolják:

$1\mapsto {\begin{pmatrix}1&0\\0&1\end{pmatrix}},\quad \mathrm {i} \mapsto {\begin{pmatrix}\mathrm {i} _{\mathbb {C} }&0\\0&-\mathrm {i} _{\mathbb {C} }\end{pmatrix}},\quad \mathrm {j} \mapsto {\begin{pmatrix}0&1\\-1&0\end{pmatrix}},\quad \mathrm {k} \mapsto {\begin{pmatrix}0&\mathrm {i} _{\mathbb {C} }\\\mathrm {i} _{\mathbb {C} }&0\end{pmatrix}},$

ahol is a komplex képzetes egységet $\mathrm {i} _{\mathbb {C} }$ jelöli az egyértelműség kedvéért.

Ebben az ábrázolásban

$\mathrm {i} \mapsto \mathrm {i} _{\mathbb {C} }\sigma _{3},\quad \mathrm {j} \mapsto \mathrm {i} _{\mathbb {C} }\sigma _{2},\quad \mathrm {k} \mapsto \mathrm {i} _{\mathbb {C} }\sigma _{1},$

ahol $\sigma _{i}$ az i-edik Pauli-mátrixot jelöli.

Eszerint a kvaterniók halmaza megfelel a

${\bigg \{}{\begin{pmatrix}w&z\\-{\overline {z}}&{\overline {w}}\end{pmatrix}}\,{\bigg |}\,w,z\in \mathbb {C} {\bigg \}}.$

mátrixok halmazának.

Ezeknek a mátrixoknak mindig $|w|^{2}+|z|^{2}$ a determinánsa, amiből már következik a nullosztómentesség, hiszen a mátrixok gyűrűjében a nullosztók determinánsa nulla, itt pedig az összes nem nulla mátrix determinánsa pozitív. A műveletek asszociativitása a mátrixműveletek asszociativitásából következik. Az $\mathrm {i} ,\mathrm {j} ,\mathrm {k}$ szorzására vonatkozó szabályok egyszerű számolással igazolhatók.

A kvaterniók másként is ábrázolhatók a komplex számok fölötti $C^{2\times 2}$-es mátrixok gyűrűjében, de az összes többi lehetőség konjugált a már leírt változathoz.

Hányadosalgebra

Az absztrakt algebra lehetőséget ad a kvaterniók hányadosalgebraként történő definiálására. Eszerint a kvaterniók előállnak a háromhatározatlanú polinomok nem kommutatív gyűrűjének a Hamilton-szorzásszabályok alkotta ideállal vett faktoraként.

Egy másik módszerhez elég két határozatlan. Ekkor a kvaterniók algebrája az $i\mapsto e_{1},\,j\mapsto e_{2},\,k=ij\mapsto e_{1}e_{2}$ által generált kétdimenziós euklideszi sík Clifford-algebrájaként áll elő.

A Clifford-algebrák egységelemes asszociatív algebrák, amiket egy kvadratikus alakkal ellátott vektortér generál. A Cℓ(V,Q) Clifford-algebra a legszabadabb algebra azzal a kikötéssel, hogy:

$v^{2}=Q(v)1$ minden $v\in V.$

A háromdimenziós forgatásokkal való összefüggésben fontos szerephez jut az, hogy a kvaterniók algebrája az $i\mapsto e_{2}e_{3},\,j\mapsto e_{3}e_{1},\,k\mapsto e_{1}e_{2}$ által generált euklideszi tér Clifford-algebrájának páros részének tekinthető.

Alapműveletek

Valós és képzetes rész

Az

$x_{0}+x_{1}\cdot \mathrm {i} +x_{2}\cdot \mathrm {j} +x_{3}\cdot \mathrm {k}$

kvaternió valós része:

$\mathrm {Re} \,x=x_{0},$

míg a többi koordináta a képzetes részhez tartozik:

$\mathrm {Im} \,x=x_{1}\cdot \mathrm {i} +x_{2}\cdot \mathrm {j} +x_{3}\cdot \mathrm {k}$

A képzetes részt gyakran a valós háromdimenziós vektorok vektorterével azonosítják:

$(x_{1},x_{2},x_{3})\in \mathbb {R} ^{3}$.

Ha az $x_{0}+x_{1}\cdot \mathrm {i} +x_{2}\cdot \mathrm {j} +x_{3}\cdot \mathrm {k}$ kvaterniókat a valós skalárból és a háromdimenziós vektorból álló párokkal azonosítjuk:

$(s,{\vec {v}})$, ahol $s=x_{0}$ és ${\vec {v}}=(x_{1},x_{2},x_{3})$,

akkor a szorzás felírható így:

$(s,{\vec {v}})\cdot (t,{\vec {w}})={\Big (}st-\langle {\vec {v}},{\vec {w}}\rangle ,\quad s{\vec {w}}+t{\vec {v}}+{\vec {v}}\times {\vec {w}}{\Big )}.$

A valós számok azonosíthatók azokkal a kvaterniókkal, amiknek képzetes része a nullvektor.

Azokat a kvaterniókat, amiknek a valós része nulla, tiszta, vagy tisztán képzetes kvaternióknak nevezik. Ezek éppen azok a kvaterniók, aminek négyzete valós, és nem pozitív. A tisztán képzetes kvaterniók halmaza:

$\mathbb {H} _{\text{Rein}}=\mathrm {Im} \,\mathbb {H} =\{x\in \mathbb {H} \mid \mathrm {Re} \,x=0\}=\{x\in \mathbb {H} \mid x^{2}\in \mathbb {R} ,\ x^{2}\leq 0\}.$

Ez egy háromdimenziós vektortér, aminek egy bázisa $\{\mathrm {i} ,\mathrm {j} ,\mathrm {k} \}$.

Két tiszta képzetes kvaternió szorzatában a valós rész a tisztán képzetes kvaterniók skaláris szorzatának mínusz egyszerese; a képzetes rész a tisztán képzetes kvaterniók vektoriális szorzataként előálló tisztán képzetes kvaternió:

$(0,{\vec {v}})\cdot (0,{\vec {w}})={\Big (}{-\langle {\vec {v}},{\vec {w}}\rangle },\quad {\vec {v}}\times {\vec {w}}{\Big )}.$

Konjugálás és norma

Egy kvaternió konjugáltjában a valós rész ugyanaz, a képzetes rész ellentett:

${\overline {x_{0}+x_{1}i+x_{2}j+x_{3}k}}=x_{0}-x_{1}i-x_{2}j-x_{3}k$

A konjugált másként is kifejezhető:

${\overline {q}}=-{\frac {1}{2}}\left(q+\mathrm {i} \cdot q\cdot \mathrm {i} +\mathrm {j} \cdot q\cdot \mathrm {j} +\mathrm {k} \cdot q\cdot \mathrm {k} \right)$

A konjugálás legfontosabb tulajdonságai:

• ${\overline {({\bar {x}})}}=x$, a konjugált konjugáltja az eredeti kvaternió
• ${\overline {x+y}}={\bar {x}}+{\bar {y}}$ és
  ${\overline {\lambda x}}=\lambda \cdot {\bar {x}}$ minden valós λ számra, vagyis a konjugálás lineáris leképezés $\mathbb {R}$ fölött
• ${\overline {x\cdot y}}={\bar {y}}\cdot {\bar {x}}$
• $x\cdot {\bar {x}}=x_{0}^{2}+x_{1}^{2}+x_{2}^{2}+x_{3}^{2}$, az $(x_{0},x_{1},x_{2},x_{3})$ vektorok normája mindig valós, és sohasem negatív

Ezt a mennyiséget az ${x_{0}+x_{1}i+x_{2}j+x_{3}k}=$ kvaternió normájának is nevezik.

Erre a normára teljesül az

$|x\cdot y|=|x|\cdot |y|.$

összefüggés, így ezzel a normával a kvaterniók Banach-algebrát alkotnak.

Ahogy a komplex számoknál, úgy a kvaternióknál is megadható a valós és a képzetes rész a konjugálás segítségével:

• ${\frac {x+{\bar {x}}}{2}}$ a valós rész;
• ${\frac {x-{\bar {x}}}{2}}$ a képzetes rész.

Ha egy kvaternió megegyezik a konjugáltjával, akkor valós. Ha a konjugálás ellentettjére változtatja, akkor tisztán képzetes.

A norma kifejezhető a konjugálással:

$|x|={\sqrt {x\cdot {\bar {x}}}}$

Invertálás

Az $x\neq 0$ kvaternió inverze az az x⁻¹ kvaternió, amivel

$x\cdot x^{-1}=1\quad$ és $\quad x^{-1}\cdot x=1.$

Mivel a szorzás nem kommutatív, azért kétféle osztás definiálható:

$b\cdot a^{-1}\quad$ és $\quad a^{-1}\cdot b,$

amik rendre a

$xa=b\quad$ és az $\quad ax=b$

egyenleteket oldják meg.

A két egyenlet megoldása akkor és csak akkor egyezik meg, ha a valós, mert csak a valósok cserélhetők fel az összes kvaternióval. Az absztrakt algebra nyelvén úgy mondjuk, hogy a kvaterniók ferdetestének centruma a valós számok halmaza. Így a $\textstyle {\frac {b}{a}}$ kifejezésbe hallgatólagosan beleértjük, hogy a valós.

Ezen kívül teljesül

$a^{-1}\cdot b^{-1}=(b\cdot a)^{-1},$

ugyanis

$a^{-1}\cdot b^{-1}\cdot b\cdot a=1\quad$

és

$\quad (b\cdot a)^{-1}\cdot b\cdot a=1.$

Ezzel egy $x\neq 0$ kvaternió inverze

$x^{-1}={\frac {\bar {x}}{|x|^{2}}},$

mivelhogy

$x^{-1}=({\bar {x}}\cdot {\bar {x}}^{-1})\cdot x^{-1}={\bar {x}}\cdot ({\bar {x}}^{-1}\cdot x^{-1})={\bar {x}}\cdot (x\cdot {\bar {x}})^{-1}={\bar {x}}\cdot (|x|^{2})^{-1}.$

$|x|^{2}$ valós, és $\neq 0$, ezért ez a kifejezés tört alakban is írható:

${\frac {\bar {x}}{|x|^{2}}}.$

Egységkvaterniók

Az egységkvaterniók az 1 normájú kvaterniók. Az 1 abszolútértékű komplex számokhoz hasonlóan

${\bar {x}}=x^{-1}.$

Tetszőleges $x\neq 0$ kvaternióra

${\frac {x}{|x|}}={\frac {x_{0}}{|x|}}+{\frac {x_{1}}{|x|}}\cdot \mathrm {i} +{\frac {x_{2}}{|x|}}\cdot \mathrm {j} +{\frac {x_{3}}{|x|}}\cdot \mathrm {k}$

az x kvaternióval megegyező irányú egységkvaternió.

Egységkvaternió inverze újra egységkvaternió. Két egységkvaternió szorzata megint egységkvaternió. A szorzás asszociativitása miatt az egységkvaterniók csoportot alkotnak a szorzásra.

Az

$\{\pm 1,\pm \mathrm {i} ,\pm \mathrm {j} ,\pm \mathrm {k} \}.$: $\{\pm 1,\pm \mathrm {i} ,\pm \mathrm {j} ,\pm \mathrm {k} \}.$

kvaterniók szintén egységkvaterniók. Részcsoportot alkotnak az egységkvaterniók csoportjában, az úgynevezett kvaterniócsoportot.

A Lie-csoport olyan csoport, ami a szorzáson és az invertáláson kívül még egy topológiával is el van látva, amire nézve az előbbi műveletek folytonosak.

Az egységkvaterniók halmaza egy háromdimenziós gömbfelszín a négydimenziós térben, ami ezzel Lie-csoporttá válik. A hozzá tartozó Lie-algebra a tiszta kvaterniók tere. A mátrixos ábrázolásban az egységkvaterniók csoportját éppen az SU(2) speciális unitér csoport ábrázolja. Ez megmagyarázza a kapcsolatot a Pauli-mátrixokkal.

A tiszta egységkvaterniók éppen azok a kvaterniók, amiknek négyzete -1:

$x_{0}=0\land x_{1}^{2}+x_{2}^{2}+x_{3}^{2}=1\qquad \iff \qquad x^{2}=-1.$

Geometriailag a tiszta egységkvaterniók egy kétdimenziós gömbfelszínt alkotnak a háromdimenziós térben. Minden kvaternió, aminek $-1$ a négyzete, definiálja a komplex számok egy beágyazását:

$\mathbb {C} \to \mathbb {H} ,\qquad a+b\mathrm {i} \mapsto a+bx,\quad a,b\in \mathbb {R} .$

De ez csak egy beágyazás. A kvaterniók nem alkotnak algebrát a komplex számok fölött.

Trigonometrikus alak

Ahogy a komplex számok,

$z=|z|\cdot (\cos \phi +\mathrm {i} \sin \phi )=|z|\cdot \mathrm {e} ^{\mathrm {i} \phi }$

úgy a kvaterniók is leírhatók trigonometrikus alakban.

Az $x\neq \pm 1$ tiszta egységkvaterniók trigonometrikus alakja:

$x=\cos \alpha +v\cdot \sin \alpha$

és ez egyértelmű, ha $0<\alpha <\pi \$

A kvaterniókra kiterjesztett exponenciális függvény segítségével:

$x=\exp(\alpha v);\$

más szóval: az exponenciális leképezés bijekció az $<\pi \$ normájú tiszta kvaterniók halmaza és a -1 nélküli egységkvaterniók halmaza között.

Általánosabban, minden nem valós kvaternió egyértelműen felírható, mint

$x=|x|\cdot (\cos \alpha +v\sin \alpha )$

ahol $\alpha ,v$, mint előbb

vagy a negatív valós számokon kívüli kvaterniók

$x=|x|\cdot \exp X$,

ahol $X$ tiszta kvaternió, amire $|X|<\pi \$.

Konstrukciók kvaterniókkal

Szorzatok

Két kvaternió képzetes részének vektoriális szorzata a két kvaternió kommutátorának kétszerese:

Ha $x=(s,{\vec {v}})$ és $y=(t,{\vec {w}})$,

akkor

${\vec {v}}\times {\vec {w}}={\frac {x\cdot y-y\cdot x}{2}}.$

Két kvaternió, mint négydimenziós vektor skalárszorzata éppen ${\bar {x}}\cdot y$ vagy $x\cdot {\bar {y}}$:

$x_{0}y_{0}+x_{1}y_{1}+x_{2}y_{2}+x_{3}y_{3}=\mathrm {Re} ({\bar {x}}y)=\mathrm {Re} (x{\bar {y}}).$

A kvaternió koordinátái megadhatók, mint

$x_{0}=\mathrm {Re} \,x,\quad x_{1}=-\mathrm {Re} (\mathrm {i} x),\quad x_{2}=-\mathrm {Re} (\mathrm {j} x),\quad x_{3}=-\mathrm {Re} (\mathrm {k} x).$

Két kvaternió Minkowski-skalárszorzata az xy szorzat valós része:

$x_{0}y_{0}-x_{1}y_{1}-x_{2}y_{2}-x_{3}y_{3}=\mathrm {Re} (xy).\$

Vektoranalízis

A következőkben azonosítjuk a tiszta kvaterniókat $\mathbb {R} ^{3}$ vektoraival.

Ha így definiáljuk a nabla operátort:

$\nabla =\mathrm {i} \cdot {\frac {\partial }{\partial x}}+\mathrm {j} \cdot {\frac {\partial }{\partial y}}+\mathrm {k} \cdot {\frac {\partial }{\partial z}},$

és az

${\vec {F}}(x,y,z)=u(x,y,z)\cdot \mathrm {i} +v(x,y,z)\cdot \mathrm {j} +w(x,y,z)\cdot \mathrm {k}$

vektormezőre alkalmazzuk, akkor kapjuk, hogy:

$\nabla {\vec {F}}=-\mathrm {div} \,{\vec {F}}+\mathrm {rot} \,{\vec {F}}.$

Itt $-\mathrm {div} \,{\vec {F}}$ a valós, $\mathrm {rot} \,{\vec {F}}$ a képzetes rész.

A nabla operátort kéteszer az $f(x,y,z)$ függvényre alkalmazva:

$\nabla ^{2}f=-\triangle f=-\left({\frac {\partial ^{2}f}{\partial x^{2}}}+{\frac {\partial ^{2}f}{\partial y^{2}}}+{\frac {\partial ^{2}f}{\partial z^{2}}}\right),$

azaz a $\nabla$ operátor úgy hat, mint a Laplace-operátor négyzetgyöke.

Forgatások a háromdimenziós térben

Az egységkvaterniók elegáns módot kínálnak a forgatások leírására a háromdimenziós térben: rögzített q kvaternióra a

$\rho _{q}\colon x\mapsto qx{\bar {q}}$

leképezés forgatás $\mathrm {Im} \,\mathbb {H}$-ben.

Ha trigonometrikus alakba írjuk a q kvaterniót:

$q=\cos \alpha +v\cdot \sin \alpha$

ahol $0<\alpha <\pi \$, és $v\$ tiszta egységkvaternió, akkor a forgatás szöge $2\alpha \$, és tengelye $v\in \mathbb {R} ^{3}$.

Minden q egységkvaternió ugyanazt a forgatást definiálja, mint -q; például 1 és -1 is az identitásnak felel meg. Tehát az ortogonális mátrixokkal ellenben ez a megfeleltetés nem egy-egyértelmű: minden R forgatáshoz két egységkvaternió van, amire $\rho _{q}=R$.

Forgatások egymásutánja, más néven szorzata az egységkvaterniók szorzásának felel meg:

$\rho _{q_{1}}\circ \rho _{q_{2}}=\rho _{q_{1}\cdot q_{2}}.$

A forgásirány megfordítása a konjugálás megfelelője:

$\rho _{\bar {q}}=\rho _{q}^{-1},$

ami az egységkvaterniók körében ugyanaz, mint az invertálás.

Mindezek miatt ez a leképezés homomorfizmus, de nem izomorfizmus.

Kapcsolat az ortogonális mátrixokkal

A $q=w+x\cdot \mathrm {i} +y\cdot \mathrm {j} +z\cdot \mathrm {k} ,\qquad w^{2}+x^{2}+y^{2}+z^{2}=1,$ egységkvaterniónak megfelelő ortogonális mátrix

${\begin{pmatrix}w^{2}+x^{2}-y^{2}-z^{2}&-2wz+2xy&2wy+2xz\\2wz+2xy&w^{2}-x^{2}+y^{2}-z^{2}&-2wx+2yz\\-2wy+2xz&2wx+2yz&w^{2}-x^{2}-y^{2}+z^{2}\end{pmatrix}}$

${}={\begin{pmatrix}1-2(y^{2}+z^{2})&-2wz+2xy&2wy+2xz\\2wz+2xy&1-2(x^{2}+z^{2})&-2wx+2yz\\-2wy+2xz&2wx+2yz&1-2(x^{2}+y^{2})\end{pmatrix}}.$

A mátrixból a kvaterniók meghatározásához elég a forgatás tengelyét és szögét megadni, és a trigonometrikus képletbe behelyettesíteni.

Kapcsolat az Euler-szögekkel

Az Euler-szögekre különféle konvenciók vannak. Itt azokat a forgatásokat tekintjük, amik megkaphatók úgy, hogy először a z tengely körül $\Phi$, utána az új x tengely körül $\Theta$, végül az új z tengely körül $\Psi$ szöggel forgatva kapunk. Az egyes forgatások rendre a

$\cos {\frac {\Phi }{2}}+\mathrm {k} \cdot \sin {\frac {\Phi }{2}},\quad \cos {\frac {\Theta }{2}}+\mathrm {i} \cdot \sin {\frac {\Theta }{2}},\quad \cos {\frac {\Psi }{2}}+\mathrm {k} \cdot \sin {\frac {\Psi }{2}},$

kvaternióknak felelnek meg.

Mivel az elforgatott tengelyt forgatjuk, a szorzás sorrendje fordított:

$\left(\cos {\frac {\Phi }{2}}+\mathrm {k} \cdot \sin {\frac {\Phi }{2}}\right)\left(\cos {\frac {\Theta }{2}}+\mathrm {i} \cdot \sin {\frac {\Theta }{2}}\right)\left(\cos {\frac {\Psi }{2}}+\mathrm {k} \cdot \sin {\frac {\Psi }{2}}\right)$

${}=\cos {\frac {\Phi }{2}}\cos {\frac {\Theta }{2}}\cos {\frac {\Psi }{2}}-\sin {\frac {\Phi }{2}}\cos {\frac {\Theta }{2}}\sin {\frac {\Psi }{2}}$

${}+\mathrm {i} \cdot \left(\cos {\frac {\Phi }{2}}\sin {\frac {\Theta }{2}}\cos {\frac {\Psi }{2}}+\sin {\frac {\Phi }{2}}\sin {\frac {\Theta }{2}}\sin {\frac {\Psi }{2}}\right)$

${}+\mathrm {j} \cdot \left(-\cos {\frac {\Phi }{2}}\sin {\frac {\Theta }{2}}\sin {\frac {\Psi }{2}}+\sin {\frac {\Phi }{2}}\sin {\frac {\Theta }{2}}\cos {\frac {\Psi }{2}}\right)$

${}+\mathrm {k} \cdot \left(\sin {\frac {\Phi }{2}}\cos {\frac {\Theta }{2}}\cos {\frac {\Psi }{2}}+\cos {\frac {\Phi }{2}}\cos {\frac {\Theta }{2}}\sin {\frac {\Psi }{2}}\right).$

Hasonlók adódnak más konvenciók esetén is.

A forgáscsoport univerzális fedése

Az egységnyi kvaterniók:

${\begin{aligned}q&{}=w+{\mathbf {i}}x+{\mathbf {j}}y+{\mathbf {k}}z,\\1&{}=w^{2}+x^{2}+y^{2}+z^{2},\end{aligned}}$

csoportja izomorf a 2*2-es, unitér mátrixok - SU(2) - csoportjával, amiért az egységkvaterniókat azonosíthatjuk a SU(2) generátoraival:

$q=a\mathrm {1} +b\mathrm {i} +c\mathrm {j} +d\mathrm {k} =\alpha +j\beta \leftrightarrow {\begin{bmatrix}\alpha &-{\overline {\beta }}\\\beta &{\overline {\alpha }}\end{bmatrix}}=U,\quad q\in \mathbb {H} ,\quad a,b,c,d\in \mathbb {R} ,\quad \alpha ,\beta \in \mathbb {C} ,\quad U\in \mathrm {SU} (2).$

Másrészről találunk az egységnyi kvaterinók csoportjából egy 2:1 művelettartó leképezést (homomorfizmust) az SO(3) forgatáscsoportba, ugyanis q és -q ugyanahhoz a Q rotációs mátrixhoz tartozik. Általánosan a (x,y,z) vektor körül 2θ szöggel forgató (ahol cos θ = w és |sin θ| = ||(x,y,z)||) Q mátrix:

$Q={\begin{bmatrix}1-2y^{2}-2z^{2}&2xy-2zw&2xz+2yw\\2xy+2zw&1-2x^{2}-2z^{2}&2yz-2xw\\2xz-2yw&2yz+2xw&1-2x^{2}-2y^{2}\end{bmatrix}},\quad Q\in \mathrm {SO} (3).$

Ez egy kétrétegű fedés, aminek magja a $\{\pm 1\}$ centrum. A fedés univerzális, hiszen $\mathrm {SU} (2)\cong S^{3}$ egyszeresen összefüggő. Spincsoportnak is nevezik, és $\mathrm {Spin} (3)$-mal is jelölik, és szorosan kapcsolódik a fizikai spinhez. Az $\mathrm {SU} (2)$ → $\mathbb {C} ^{2}$ leképezés egy úgynevezett spinorábrázolás, azaz egy olyan ábrázolás, amiben a négyzetes mátrixok mérete páros. Három báziskvaternió, i, j és k az SU(2) három hermitikus generáló mátrixának, a Pauli-mátrixoknak felel meg:

$\sigma _{x}:={\begin{pmatrix}0,1\\1,0\end{pmatrix}}$ ,    $\sigma _{y}:={\begin{pmatrix}0,-i\\+i,0\end{pmatrix}}$ ,    $\sigma _{z}:={\begin{pmatrix}+1,0\\0,-1\end{pmatrix}}$ 

Így függ össze a két alaptétel:

i = σ_x/i, j = σ_y/i és k = σ_z/i,

ahol i a komplex képzetes egység, így az elméleti fizikából ismert σ_xσ_y= iσ_z kapcsolat éppen az i $\cdot$ j=k relációnak felel meg. A σ-mátrixok hermitikus voltuk miatt mérhető mennyiségekként jöhetnek szóba a kvantummechanikában, ellentétben a i, j és a k báziskvaterniókkal, ami fontos a kvantummechanika matematikai modellezésében. Közelebbről $\mathrm {SU(2)} \equiv \{\exp(i{\frac {1}{2}}{\vec {\alpha }}\cdot {\vec {\sigma }})\}$, aminek valós vektorkoordinátái α_x, α_y és α_z. Az 1/2 szorzónak többek között az a hatása,hogy a spinorok a vektorokkal ellentétben nem kerülnek vissza alaphelyzetükbe 2π-vel  (=360 fokkal) elforgatva, hanem csak annak kétszerese után.

A négydimenziós tér ortogonális leképezései

A háromdimenziós esethez hasonlóan $\mathbb {H}$ minden irányítástartó hasonlósági transzformációja felírható, mint:

$\rho _{a,b}\colon x\mapsto ax{\bar {b}}$

az $a,b$ egységkvaterniókkal.

Teljesül, hogy:

$\rho _{a_{1},b_{1}}\circ \rho _{a_{2},b_{2}}=\rho _{a_{1}a_{2},b_{1}b_{2}}\quad \mathrm {und} \quad \rho _{{\bar {a}},{\bar {b}}}=\rho _{a,b}^{-1}.$

Ez a konstrukció fedést ad:

$\mathrm {SU} (2)\times \mathrm {SU} (2)\to \mathrm {SO} (4)$

aminek magja $\{(1,1),(-1,-1)\}$.

A kvaterniók algebrája

Izomorfia erejéig három véges dimenziós asszociatív algebra van a valós számok felett: saját maga, algebrai lezártja, és a felette vett kvaterniók.

$\mathbb {H}$ centruma $\mathbb {R}$, ezért definiálható rajta redukált norma és redukált nyom:

$\mathrm {Nrd} (x)=|x|^{2}\quad$és $\quad \mathrm {Trd} (x)=2\cdot \mathrm {Re} \,x$

A valós számokról a komplex számokra áttérve a kvaterniók algebrája mátrixalgebrává válik:

$\mathbb {H} \otimes _{\mathbb {R} }\mathbb {C} \cong M_{2}(\mathbb {C} ).$

A tenzorszorzat $\mathbb {C}$ faktorra vett komplex konjugáció involúciót szolgáltat a mátrixalgebrában, aminek invariánsai egy $\mathbb {H}$-val izomorf algebrát alkotnak.

Az

$A\mapsto w{\bar {A}}w^{-1},$ ahol az $w={\begin{pmatrix}0&1\\-1&0\end{pmatrix}}$

involúció megfelel a kvaterniók fenti mátrixmodelljének.

A kvaterniók algebrája egy negatív definit szimmetrikus kvadratikus alakkal ellátott $\mathbb {R} ^{2}$ Clifford-algebrájának tekinthető.

Alkalmazásai

A kvaterniók legfontosabb haszna, hogy a tisztán képzetes (azaz a valós része, az 'a' komponens 0) számokkal leírható a háromdimenziós vektortér. A kvaterniókat a háromdimenziós mozgásokkal való szoros kapcsolata miatt felhasználják robotok vezérlésénél.

A kvaterniókat CAD programok is felhasználják a térbeli elforgatások kezelésére és az elforgatás tengelyének és szögének tárolására, ugyanis egy kvaternióhoz csak 4 lebegőpontos adatot kell tárolni (a tengellyel együtt), szemben az elforgatási mátrix 3×3 elemével és az elforgatás tengelyéhez szükséges további 3 elemmel. A kvaternió könnyedén átalakítható elforgatási mátrix alakba, és a kvaterniókkal való számítások gyakran kevesebb műveletet igényelnek, mint a vektoros–mátrixos számítások. Kvaterniókat alkalmaz pl. a MicroStation CAD program.

Négynégyzetszám-tétel

Legyen

$x_{1}=a_{1}+b_{1}\cdot \mathrm {i} +c_{1}\cdot \mathrm {j} +d_{1}\cdot \mathrm {k} \quad$ és $\quad x_{2}=a_{2}+b_{2}\cdot \mathrm {i} +c_{2}\cdot \mathrm {j} +d_{2}\cdot \mathrm {k}$

Az

$|x_{1}|^{2}\cdot |x_{2}|^{2}=|x_{1}x_{2}|^{2}$

egyenlőségből adódik a tisztán valós azonosság:

$(a_{1}^{2}+b_{1}^{2}+c_{1}^{2}+d_{1}^{2})(a_{2}^{2}+b_{2}^{2}+c_{2}^{2}+d_{2}^{2})$

${}=(a_{1}a_{2}-b_{1}b_{2}-c_{1}c_{2}-d_{1}d_{2})^{2}+(a_{1}b_{2}+b_{1}a_{2}+c_{1}d_{2}-d_{1}c_{2})^{2}\,$

${}+(a_{1}c_{2}-b_{1}d_{2}+c_{1}a_{2}+d_{1}b_{2})^{2}+(a_{1}d_{2}+b_{1}c_{2}-c_{1}b_{2}+d_{1}a_{2})^{2}.\,$

Ha az összes szám egész, akkor ez az egyenlőség azt állítja, hogy két, négy négyzetszám összegeként felírható szám szorzata szintén felírható négy négyzetszám összegeként.

A négynégyzetszám-tétel szerint minden természetes szám felírható négy négyzetszám összegeként. Az előző állítás szerint elég a tételt a prímszámokra belátni. Ez alapján ezt az utóbbit is nevezik négynégyzetszám-tételnek.

Rokon témák

A kvaterniókhoz hasonló konstrukciókat hiperkomplex számoknak is nevezik. A Cayley-számok a kvaterniók nyolcdimenziós analogonjai. Az ő körükben a szorzás se nem kommutatív, se nem asszociatív. A Cayley-számok szorzása alternatív:

$a\cdot (a\cdot b)=(a\cdot a)\cdot b$ és $a\cdot (b\cdot b)=(a\cdot b)\cdot b$ minden a, b Cayley-számra.

Források

• Doing Physics with Quaternions (PDF; 563 kB)
• Serge Lang, Algebra. Springer-Verlag, New York 2002. ISBN 0-387-95385-X