Pascal-háromszög
A Pascal-háromszög a matematikában a binomiális együtthatók háromszög alakban való elrendezése. A nyugati világ nagy részén Blaise Pascalról nevezték el, noha egyes indiai, perzsa, kínai és itáliai matematikusok már évszázadokkal Pascal előtt tanulmányozták.[1][2]
A háromszögben a sorok számozása zérótól kezdődik, és a páratlan és páros sorokban a számok el vannak csúsztatva egymáshoz képest. A háromszöget a következő egyszerű módon lehet megszerkeszteni: A nulladik sorba csak be kell írni az 1-est. A következő sorok szerkesztésénél a szabály a következő: az új számot úgy kapjuk meg, ha összeadjuk a felette balra és felette jobbra található két számot. Ha az összeg valamelyik tagja hiányzik (sor széle), akkor nullának kell tekinteni. Például az 1-es sor első száma 0 + 1 = 1, míg a 2-es sor középső száma 1 + 1 = 2.
Ez a szerkesztés Pascal képletén alapul, amely szerint
a k-adik binomiális együttható az (x+y)n kifejtésében, akkor
bármely nem negatív egész n és bármely 0 és n közötti egész k esetében.[3]
A Pascal-háromszögnek általánosítása három dimenzióra a Pascal-gúla, illetve a többdimenziós általánosítások neve Pascal-szimplex.
A háromszög[szerkesztés]
Itt látható a Pascal-háromszög a tizenhatodik sorig:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
1 10 45 120 210 252 210 120 45 10 1
1 11 55 165 330 462 462 330 165 55 11 1
1 12 66 220 495 792 924 792 495 220 66 12 1
1 13 78 286 715 1287 1716 1716 1287 715 286 78 13 1
1 14 91 364 1001 2002 3003 3432 3003 2002 1001 364 91 14 1
1 15 105 455 1365 3003 5005 6435 6435 5005 3003 1365 455 105 15 1
1 16 120 560 1820 4368 8008 11440 12870 11440 8008 4368 1820 560 120 16 1
A Pascal-háromszög és a binomiális kifejtés[szerkesztés]
A Pascal-háromszög megadja a binomiális kifejtés együtthatóit. Például tekintsük a
- (x + y)2 = x2 + 2xy + y2 = 1x2y0 + 2x1y1 + 1x0y2.
kifejtést. Látható, hogy az együtthatók a Pascal-háromszög kettes sorában találhatók: 1, 2, 1.
Általános esetben ha az x + y alakú binomot egész hatványra emeljük, akkor:
- (x + y)n = a0xn + a1xn‒1y + a2xn‒2y2 + … + an‒1xyn‒1 + anyn,
ahol a kifejtés ai együtthatói éppen a Pascal-háromszög n-es sorában található számok. Más szóval
Ez a binomiális tétel.
Megfigyelhető, hogy a Pascal-háromszög teljes jobb oldali átlója megfelel az yn együtthatójának, a következő átló az xyn-1 együtthatója és így tovább.
A binomiális tételnek és a Pascal-háromszög megszerkesztésének kapcsolatához tekintsük meg, hogyan lehet kiszámítani az (x + 1)n+1 kifejtésének az együtthatóit az (x + 1)n együtthatói alapján. (Az egyszerűség kedvéért legyen y = 1). Tételezzük fel, hogy
Akkor
A két összeget a következőképpen lehet átrendezni:
- (mivel a0 = an = 1)
Így most megkaptuk az (x + 1)n+1 polinom kifejtését az (x + 1)n együtthatóinak függvényében (ezek az ai-k), és pont erre van szükség, ha ki akarjuk számítani az egyik sort a felette levő sor tagjainak segítségével.
Ismétlésül:
- az átlók minden tagja a bal felsőtől indulva a jobb alsóig x azonos hatványának felel meg, * az a-tagok az (x + 1)n polinom együtthatói
- és az (x + 1)n+1 együtthatóit kell meghatároznunk.
Így minden i esetében, amely nem 0 és nem n + 1, az xi tag együtthatója az (x + 1)n+1 polinomban egyenlő ai-(ez a meghatározandó számhoz képest balra fent van) + ai‒1 (ez pedig az előzőtől rögtön jobbra). Ez pedig pont a Pascal-háromszög soronkénti szerkesztésének egyszerű szabálya.
Ez az érvelés könnyen átalakítható a binomiális tétel matematikai bizonyításává a teljes indukció módszerével.
A binomiális tétel érdekes következményét kapjuk, ha mindkét változó, x és y értékét 1-nek vesszük. Ekkor tudjuk, hogy , és így
Más szóval, a Pascal-háromszög n-edik sorában a tagok összege 2 n-edik hatványa.
Kombinációk[szerkesztés]
A Pascal-háromszög egy másik alkalmazása a kombinációk kiszámítása. Például n elem k elemű kombinációinak száma
Ez éppen a Pascal-háromszög elemeinek képlete. Hogyha adva van a Pascal-háromszög, akkor a számítás helyett elég ránézni a megfelelő elemre. Például egy 10 tagú kosárlabdacsapatból kiválasztunk 8 tagot. A választ a 10. sor 8. eleme adja meg: 45.
Tulajdonságok[szerkesztés]
A sorok[szerkesztés]
- Egy sor elemeinek összege kétszerese az előző sor összegének. A nulladik sor összege egy, ami éppen 20. Továbbá, az első sor összege 21 = 2, a másodiké 22 = 4, és így tovább, az n-edik sor összege 2n.
- Az összeg helyett a szorzatokat véve egy olyan sorozatot kapunk (Sloane A001142), ami kapcsolódik az e számhoz.[4][5]
Tehát a sorozat így definiálható:
Az egymást követő tagok hányadosa:
aminek hányadosa:
A fenti egyenlet jobb oldaláról tudjuk, hogy az e-hez tart:
- Ha minden helyet helyi értéknek tekintünk, akkor az egyes sorokat számokként összeolvasva a 10-es átlépésig 11 hatványait kapjuk. Az ez után következő soroknál átvitel képződik, amit átvíve 11 további, nagyobb kitevőjű hatványai adódnak. Más alapú számrendszerekben is az adott alapszámnál eggyel nagyobb szám hatványai tovább olvashatók le a Pascal-háromszögben az adott számrendszerben. Az összefüggés átvitellel minden számrendszerre teljesül.
- Hármas számrendszerben: 1 2 13 = 42 (16)
- ⟨1, 3, 3, 1⟩ → 2 1 0 13 = 43 (64)
- Hatos számrendszerben: 1 3 3 16 = 73 (343)
- ⟨1, 4, 6, 4, 1⟩ → 1 5 0 4 16 = 74 (2401)
- Kilences számrendszerben: 1 2 19 = 102 (100)
- 1 3 3 19 = 103 (1000)
- ⟨1, 5, 10, 10, 5, 1⟩ → 1 6 2 1 5 19 = 105 (100000)
- Tízes számrendszerben: 1 2 110 = 112 (121)
- ⟨1, 5, 10, 10, 5, 1⟩ → 1 6 1 0 5 110 = 115 (161051)
- ⟨1, 6, 15, 20, 15, 6, 1⟩ → 1 7 7 1 5 6 110 = 116 (1771561)
- Tizenhatos számrendszerben: 1 5 10 10 5 116 = 175 (1419857)
- ⟨1, 6, 15, 20, 15, 6, 1⟩ → 1 7 0 4 15 6 116 = 176 (24137569)
- Egyes számok kapcsolódnak a Lozanić-háromszöghöz.
- Az n-edik sorban levő számok négyzetösszege megegyezik a 2n-edik sor középső elemével. Például:
- 12 + 42 + 62 + 42 + 12 = 70.
- Általában:
- Ha n páros, akkor a középső termből kivonva a két balra levő termet egy Catalan-számot kapunk, mégpedig az (n/2 + 1)-edik Catalan-számot. Például a negyedik sorban 6 − 1 = 5, ami a harmadik Catalan-szám, és 4/2 + 1 = 3.
- Hogyha n = p prímszám, akkor az 1-esek kivételével a sor minden eleme osztható p-vel. Ez könnyen bizonyítható, mivel a prímszámoknak nincs valódi osztója. A háromszögben minden szám egész, így és osztója -nak. A nevezőben viszont nem található p, így az osztás elvégzésekor nem fog kiesni a számlálóból.
- Paritás: Számoljuk meg az n-edik sorban a páratlan számokat. Jelölje x n kettes számrendszerbeli alakjában az 1-esek számát. Ekkor a páratlan számok száma a sorban megegyezik 2x-szel.[6]
- Polaritás: Az egy sorban álló számokat váltakozó előjellel összeadva nullát kapunk.
Az átlók[szerkesztés]
Egyes egyszerű minták ránézésre is nyilvánvalóak a Pascal-háromszög átlóiban:
- A bal és jobb oldali átlók csak 1-eseket tartalmaznak.
- Balról és jobbról a második átlók sorrendben tartalmazzák a természetes számokat.
- Befelé haladva, a negyedik átlók a tetraéderszámokat tartalmazzák.
- Általában is igaz, hogy az átlópárok a d dimenziós háromszögszámokat tartalmazzák. Ezeket képlettel a következőképpen lehet leírni:
Más képlet:
Rekurzió nélkül:
- ahol n(d) a Pochhammer-szimbólum.
A trid függvény mértani értelmezése: minden d esetén trid(1) = 1. Szerkesszünk egy d dimenziós háromszöget oly módon, hogy az előző alakzat alá minden pont alá még egy pontot helyezünk el, amely az trid(1) = 1-nek felel meg. Ezeket az új pontokat a Pascal-háromszöghöz hasonló módon helyezzük el. A trid(x) értékének meghatározásához: x pont alkotja a sokszöget. trid(x) egyenlő a d dimenziós háromszögben található pontok számával. Egy 1 dimenziós háromszög csak egy sor, így tri1(x) = x, amely a természetes számok sorozata. A pontok száma mindegyik rétegben trid ‒ 1(x) -nak felel meg.
Egy sor vagy oszlop kiszámítása[szerkesztés]
Az egyes sorok és átlók egyszerű algoritmusokkal számolhatók, amelyek nem igénylik a faktoriálisokat vagy az előző sorokat.
Az n-edik sor kiszámítása: Az első elem az 1. A további elemek az előzőből egy törttel való szorzással állnak elő:
Például az ötödik sor:, , , és , így az elemek , , . A további elemek a szimmetria tulajdonság alapján az előbbiek tükörképei.
Az , , , ... elemeket tartalmazó átló kiszámítására újra -gyel kezdünk, és a további elemek a
törtekkel való szorzással kaphatók.
Például az -val kezdődő átlón a törtek: , , , ..., így az elemek , , . A további elemek a szimmetria tulajdonság miatt az előzőek tükörképei.
Egyéb mintázatok és tulajdonságok[szerkesztés]

- Az a minta, amelyet akkor kapunk, ha a Pascal-háromszögben a páratlan számokat kiszínezzük, a Sierpiński-háromszögnek nevezett fraktálra emlékeztet, és ez a hasonlóság annál erősebb, minél több sort veszünk figyelembe. Határértékben, ha a sorok száma tart a végtelenhez, az így létrejövő minta maga a Sierpiński-háromszög. Ha a számok közül a 3, 4 stb. többszöröseit színezzük ki, egyéb mintázatokat kapunk.

- Képzeljük el, hogy a háromszögben minden szám csomópont egy hálózatban, összekötve az alatta és felette levő sorban található szomszédos számokkal. Most számoljuk meg minden csomóponthoz az utak számát, amely a legfelső ponthoz vezet – ez éppen a csomópontban található Pascal-szám lesz.
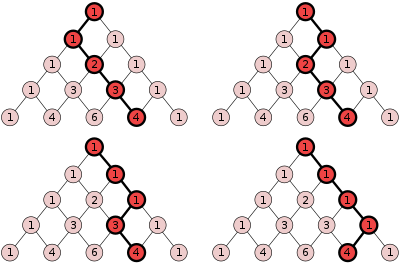
- Egy további tulajdonság akkor válik nyilvánvalóvá, ha a háromszög sorait balra igazítjuk. Ekkor az (azonos színnel megjelölt) átlók mentén képezve az összegeket, a Fibonacci-számokat kapjuk. (Például, a kék átlóval kezdve, 1 + 3 + 1 = 5, 1 + 4 + 3 = 8, 1 + 5 + 6 + 1 = 13…)
1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 1 7 21 35 35 21 7 1 1 8 28 56 70 56 28 8 1
A Pascal háromszög tükrözése és a kölcsönösen megfeleltetett számok szorzata[szerkesztés]
- Egy példa: (OEIS) A129352 Number parallelogram based on Pascal's triangle (and special mirror of central and multiply of diagonal). http://oeis.org/A129352
Táblázat a fenti OEIS példához hasonlóan[szerkesztés]
| fix pont: karakterek száma: | "0" | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | összesen |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 12 0 vagy AAAAAAAAAAAA | 924 | 924 | ||||||||||||
| 11 1 vagy AAAAAAAAAAAB | 462 | 462 | 924 | |||||||||||
| 10 2 vagy AAAAAAAAAABB | 210 | 504 | 210 | 924 | ||||||||||
| 9 3 vagy AAAAAAAAABBB | 84 | 378 | 378 | 84 | 924 | |||||||||
| 8 4 vagy AAAAAAAABBBB | 28 | 224 | 420 | 224 | 28 | 924 | ||||||||
| 7 5 vagy AAAAAAABBBBB | 7 | 105 | 350 | 350 | 105 | 7 | 924 | |||||||
| 6 6 vagy AAAAAABBBBBB | 1 | 36 | 225 | 400 | 225 | 36 | 1 | 924 | ||||||
| 5 7 vagy AAAAABBBBBBB | 7 | 105 | 350 | 350 | 105 | 7 | 924 | |||||||
| 4 8 vagy AAAABBBBBBBB | 28 | 224 | 420 | 224 | 28 | 924 | ||||||||
| 3 9 vagy AAABBBBBBBBB | 84 | 378 | 378 | 84 | 924 | |||||||||
| 2 10 vagy AABBBBBBBBBB | 210 | 504 | 210 | 924 | ||||||||||
| 1 11 vagy ABBBBBBBBBBB | 462 | 462 | 924 | |||||||||||
| 0 12 vagy BBBBBBBBBBBB | 924 | 924 |
A fenti táblázat binomiális együtthatókkal[szerkesztés]
| fix pont: karakterek száma: | "0" | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | össz. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 12 0 vagy AAAAAAAAAAAA | C(0,0)*C(12,6) | 924 | ||||||||||||
| 11 1 vagy AAAAAAAAAAAB | C(1,0)*C(11,6) | C(1,1)*C(11,5) | 924 | |||||||||||
| 10 2 vagy AAAAAAAAAABB | C(2,0)*C(10,6) | C(2,1)*C(10,5 | C(2,2)*C(10,4) | 924 | ||||||||||
| 9 3 vagy AAAAAAAAABBB | C(3,0)*C(9,6) | C(3,1)*C(9,5) | C(3,2)*C(9,4) | C(3,3)*C(9,3) | 924 | |||||||||
| 8 4 vagy AAAAAAAABBBB | C(4,0)*C(8,6) | C(4,1)*C(8,5) | C(4,2)*C(8,4) | C(4,3)*C(8,3) | C(4,4)*C(8,2) | 924 | ||||||||
| 7 5 vagy AAAAAAABBBBB | C(5,0)*C(7,6) | C(5,1)*C(7,5) | C(5,2)*C(7,4) | C(5,3)*C(7,3) | C(5,4)*C(7,2) | C(5,5)*C(7,1) | 924 | |||||||
| 6 6 vagy AAAAAABBBBBB | C(6,0)*C(6,6) | C(6,1)*C(6,5) | C(6,2)*C(6,4) | C(6,3)*C(6,3) | C(6,4)*C(6,2) | C(6,5)*C(6,1) | C(6,6)*C(6,0) | 924 | ||||||
| 5 7 vagy AAAAABBBBBBB | C(7,1)*C(5,5) | C(7,2)*C(5,4) | C(7,3)*C(5,3) | C(7,4)*C(5,2) | C(7,5)*C(5,1) | C(7,6)*C(5,0) | 924 | |||||||
| 4 8 vagy AAAABBBBBBBB | C(8,2)*C(4,4) | C(8,3)*C(4,3) | C(8,4)*C(4,2) | C(8,5)*C(4,1) | C(8,6)*C(4,0) | 924 | ||||||||
| 3 9 vagy AAABBBBBBBBB | C(9,3)*C(3,3) | C(9,4)*C(3,2) | C(9,5)*C(3,1) | C(9,6)*C(3,0) | 924 | |||||||||
| 2 10 vagy AABBBBBBBBBB | C(10,4)*C(2,2) | C(10,5)*C(2,1) | C(10,6)*C(2,0) | 924 | ||||||||||
| 1 11 vagy ABBBBBBBBBBB | C(11,5)*C(1,1) | C(11,6)*C(1,0) | 924 | |||||||||||
| 0 12 vagy BBBBBBBBBBBB | C(12,6)*C(0,0) | 924 |
A táblázat soraiban levő számok értelmezése[szerkesztés]
Hat darab "A" és hat darab "B" objektum (AAAAAABBBBBB), (karakter) összes permutációját vessük össze a kiindulási Hat darab "A" és hat darab "B" objektum (AAAAAABBBBBB)kiindulási mintájával és vizsgáljuk meg, hogy mennyi fixpontot kapunk!
Sorra nulla, egy, kettő, … öt, tíz, tizenegy, és tizenkettő fixpont lehet. Ezeknek a darabszámát adja meg a táblázat:
6 6 vagy AAAAAABBBBBB sor :1 36 225 400 225 36 1 a fixpontok száma, ez összesen 924
Ha az összes permutációt összevetjük hasonlóképpen 12 db "A" karakterrel(AAAAAAAAAAAA), vagy 12 db "B" karakterrel (BBBBBBBBBBBB),akkor csak hat fixpont lehet a legfelső és legalsó táblázatsor szerint: 924 darab.
Értelemszerűen a táblázat további sorai is a fixpontok számát írják le.
"Fixpont" alatt az összehasonlítás során az azonos helyen megegyező karakter értendő!
lásd:
https://en.wikipedia.org/wiki/Rencontres_numbers
https://en.wikipedia.org/wiki/Cycles_and_fixed_points
https://en.wikipedia.org/wiki/Subfactorial
Még kifinomultabb minták[szerkesztés]
Vannak további meglepő, kifinomult minták is. A háromszög egy pontjából egy elnyújtott átlót képezünk úgy, hogy minden elemtől lépünk egyet jobbra és utána egyet jobbra-le, vagy ugyanezt ellenkező irányban. Ilyen például az 1, 6, 5, 1 tagokból álló vonal, amely az 1, 3, 3, 1 sorban kezdődik és három sorral lejjebb végződik. Egy ilyen "átló" tagjainak összege Fibonacci-szám. A példában ez a Fibonacci-szám 13:
1
1 1
1 2 1
1 → 3 ↓ 3 1
1 4 →6 → 4 ↓ 1
1 5 10 10 →5 → 1 ↓
1 → 6 ↓ 15 20 15 6 →1
1 7 →21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
1 10 45 120 210 252 210 120 45 10 1
1 11 55 165 330 462 462 330 165 55 11 1
1 12 66 220 495 792 924 792 495 220 66 12 1
1 13 78 286 715 1287 1716 1716 1287 715 286 78 13 1
1 14 91 364 1001 2002 3003 3432 3003 2002 1001 364 91 14 1
1 15 105 455 1365 3003 5005 6435 6435 5005 3003 1365 455 105 15 1
1 16 120 560 1820 4368 8008 11440 12870 11440 8008 4368 1820 560 120 16 1
A második megjelölt átló tagjainak összege 233. A jobbra illetve jobbra-le lépések között „kiugrott” számok összege szintén Fibonacci-szám. Például az első átlónál kiugrott számok 3, 4 és 1, amelyeknek az összege 8.
Továbbá, ha m-el jelöljük az -edik sort, akkor az m-edik sor tagjainak négyzetösszege egyenlő a -edik sor középső tagjával. Például . Általánosságban:
Másik érdekes minta, hogy bármely páratlan m esetében, az m-edik sor középső tagja mínusz a kettővel balra levő tag Catalan-szám, pontosabban a (m + 1)/2 Catalan-szám. Például az 5-ös sorban 6 ‒ 1 = 5, ami a 3-adik Catalan-szám és (5 + 1)/2 = 3.
Ezen kívül, az m sor tagjainak összege 2m‒1. Például az 5-ös sor tagjainak összege , amely . Ez a binomiális tételből következik, ha az (1 + 1)m‒1-re alkalmazzuk.
A Pascal-háromszög még egy érdekes tulajdonsága, hogy azokban a sorokban, ahol a második szám prímszám, a sorban található minden szám (az 1-esek kivételével) ennek a prímnek a többszöröse.

Mátrixhatvány[szerkesztés]
Mivel faktoriálisokból épül fel, a Pascal-háromszög felírható mátrixhatványként: a Pascal-háromszög annak a mátrixnak a hatványa, amely 1, 2, 3, 4, … számokat tartalmazza a főátló alatt, az összes többi eleme pedig nulla.
A politópok elemeinek száma[szerkesztés]
A Pascal-háromszög használható politópok elemeinek számának meghatározásához.
Például a harmadik sor 1, 3, 3, 1. Egy két dimenziós szimplex (háromszög) 2 dimenziós eleme önmaga, három oldala 1 dimenziós szimplex, három csúcsa három 0 dimenziós szimplex, és az üres halmaz egy -1 dimenziós szimplex. Hasonlóan, a tetraéder elemeinek száma is rendre 1, 4, 6, 4, 1. Magasabb dimenziós szimplexek elemeinek száma is megadható hasonló módon.
Ezt bizonyíthatjuk is, ha meggondoljuk, hogy hogyan lehet kiszámítani a szimplex adott dimenziós elemeinek számát az alap elemeinek számából. Ugyanis, ha tekintjük a konstrukciót, akkor például tetraéder esetén a háromszögnek 0 téreleme van, de keletkezik egy új. A lapok száma 1 + 3, az alap és az alap síkjára nem illeszkedő csúcs és az alap oldalai által kifeszített háromszögek. Az élek száma 3 + 3, az alap élei és az alap csúcsait az új csúccsal összekötő élek. A csúcsok száma 3 + 1, az alap csúcsai és az újonnan felvett csúcs, amelynek metszete az alappal üres. Ez megmagyarázza az üres elem felvételét. Végül az új szimplexhez is hozzávesszük az üres elemet.
A négyzetekhez hasonló minta konstruálható. A megfelelő számok egy Pascal-háromszöghöz hasonlóan képzett számháromszögből olvashatók le. amiben (x + 2)n együtthatói szerepelnek (x + 1)n együtthatói helyett. Az első két sor: a nulladik sorban 1 áll, az első sorban 1, 2. A többi elem az
szabály alapján képezhető. Szavakkal: a bal felső elem kétszereséhez adjuk a jobb elemet.
Az így kapott háromszög első néhány sora:
1
1 2
1 4 4
1 6 12 8
1 8 24 32 16
1 10 40 80 80 32
1 12 60 160 240 192 64
1 14 84 280 560 672 448 128
Ez a háromszög megkapható úgy is, hogy a Pascal-háromszög elemeit megszorozzuk 2k-nal, ahol k az adott szám pozíciója a sorban. Ebből a háromszögből a szimplexek helyett a kockák, illetve hiperkockák d dimenziós elemeinek száma olvasható le. Például egy két dimenziós kocka (négyzet) két dimenziós elemeinek száma 1, 1 dimenziós elemeinek (oldalainak) száma 4, és 0 dimenziós elemeinek (csúcsainak) száma szintén 4. Ebben a táblázatban nem szerepel az üres elem. A kocka elemeinek száma rendre 1, 6, 12 és 8. Ez a mintázat a végtelenségig ismétlődik.
A mögöttes konstrukciós elv ez: Vegyük a kockát, és toljuk el élhossznyira a hipersíkjára merőlegesen. Az ezeket összekötő szakaszokkal együtt meghatároznak egy eggyel magasabb dimenziós kockát, amit itt most nevezzünk hiperkockának. A két kocka miatt a kocka elemei megduplázódnak, emiatt kell a bal elemet kettővel szorozni. Az új elemek a szimplexhez hasonlóan keletkeznek, azzal az eltéréssel, hogy nem keletkeznek új csúcsok, emiatt nem kell számításba venni az üres elemet.
Ebben a háromszögben az m-edik sorban az elemek összege 3m − 1. Például az ötödik sorban , ami éppen .
sin(x)n+1/x Fourier-transzformációja[szerkesztés]
Ahogy a fentiekben írtuk, az n-edik sor az (x + 1)n együtthatóit tartalmazza. Az (x − 1)n együtthatói előjel nélkül ugyanezek, előjelesen pedig váltakozva pozitív és negatív előjelűek. Normalizálás után ugyanezek a számok jelennek meg sin(x)n+1/x Fourier-együtthatóiként. Pontosabban: ha n páros, akkor vegyük a valós részt, ha páratlan, akkor a képzetes részt. Ekkor az eredmény egy lépcsős függvény, amelynek értékei normalizálás után a háromszög n-edik sorában álló számok váltakozó előjellel.[7]
Például, a
függvényből kapott lépcsős függvény együtthatói előjel nélkül a háromszög 4. sorában találhatók. A villamosmérnökök által gyakran használt eset:
egy négyszögjel.[8] Ennek a háromszögben a nulladik sor felel meg, ami egyetlen egyesből áll.
Ha n 4-gyel osztva 2-t vagy 3-at ad maradékul, akkor az n-edik sor -1-gyel kezdődik. Az első elemek sorozata a képzetes egység ciklikusan ismétlődő hatványainak felel meg:
Sejtautomaták[szerkesztés]
Az egy dimenziós életjáték az időben Pascal-háromszögre (modulo 2), illetve Sierpinski-háromszögre emlékeztető alakzatokat formál a 60-as szabállyal, ahol a fekete sejtek a páratlan számoknak felelnek meg.[9] A 102-es szabállyal ugyanezek az alakzatok jelennek meg, hogyha eltekintünk a vezető nulláktól. A 90-es szabály szintén ilyen alakzatokat állít elő, de az alakzat minden sejtjét egy fekete (halott) sejt választja el.
Kiterjesztések[szerkesztés]
A Pascal-háromszög a negatív számokkal jelzett sorokra is kiterjeszthető:
Először is írjuk fel a háromszöget a következő alakban:
| m = 0 | m = 1 | m = 2 | m = 3 | m = 4 | m = 5 | ... | |
| n = 0 | 1 | 0 | 0 | 0 | 0 | 0 | ... |
| n = 1 | 1 | 1 | 0 | 0 | 0 | 0 | ... |
| n = 2 | 1 | 2 | 1 | 0 | 0 | 0 | ... |
| n = 3 | 1 | 3 | 3 | 1 | 0 | 0 | ... |
| n = 4 | 1 | 4 | 6 | 4 | 1 | 0 | ... |
Terjesszük ki az 1-esek oszlopát a negatív irányba:
| m = 0 | m = 1 | m = 2 | m = 3 | m = 4 | m = 5 | ... | |
| n = −4 | 1 | ... | |||||
| n = −3 | 1 | ... | |||||
| n = −2 | 1 | ... | |||||
| n = −1 | 1 | ... | |||||
| n = 0 | 1 | 0 | 0 | 0 | 0 | 0 | ... |
| n = 1 | 1 | 1 | 0 | 0 | 0 | 0 | ... |
| n = 2 | 1 | 2 | 1 | 0 | 0 | 0 | ... |
| n = 3 | 1 | 3 | 3 | 1 | 0 | 0 | ... |
| n = 4 | 1 | 4 | 6 | 4 | 1 | 0 | ... |
Tudjuk, hogy:
ami átrendezhető a következő alakba:
így a negatív sorokban álló többi szám is számítható:
| m = 0 | m = 1 | m = 2 | m = 3 | m = 4 | m = 5 | ... | |
| n = −4 | 1 | −4 | 10 | −20 | 35 | −56 | ... |
| n = −3 | 1 | −3 | 6 | −10 | 15 | −21 | ... |
| n = −2 | 1 | −2 | 3 | −4 | 5 | −6 | ... |
| n = −1 | 1 | −1 | 1 | −1 | 1 | −1 | ... |
| n = 0 | 1 | 0 | 0 | 0 | 0 | 0 | ... |
| n = 1 | 1 | 1 | 0 | 0 | 0 | 0 | ... |
| n = 2 | 1 | 2 | 1 | 0 | 0 | 0 | ... |
| n = 3 | 1 | 3 | 3 | 1 | 0 | 0 | ... |
| n = 4 | 1 | 4 | 6 | 4 | 1 | 0 | ... |
Ez a kiterjesztés megőrzi azt a tulajdonságot, hogy az m-edik oszlop n függvényeként az
polinom együtthatói.
Továbbá az n-edik sorban (1 + x)n együtthatói állnak:
Például:
Sorozatként tekintve a negatív sorok divergálnak, azonban még mindig Abel-összegezhetők maradnak, és Abel-összegük 2n. Az n = -1 sorozat a Grandi-sorozat, amelynek Abel-összege 1/2, és n = -2 számú sor éppen az 1 − 2 + 3 − 4 + · · ·, aminek Abel-összege 1/4.
A kiterjesztés másik módja a másik átló egyeseit folytatja:
| m = −4 | m = −3 | m = −2 | m = −1 | m = 0 | m = 1 | m = 2 | m = 3 | m = 4 | m = 5 | ... | |
| n = −4 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... |
| n = −3 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | |
| n = −2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | ||
| n = −1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | ... | |||
| n = 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | ... |
| n = 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | ... |
| n = 2 | 0 | 0 | 0 | 0 | 1 | 2 | 1 | 0 | 0 | 0 | ... |
| n = 3 | 0 | 0 | 0 | 0 | 1 | 3 | 3 | 1 | 0 | 0 | ... |
| n = 4 | 0 | 0 | 0 | 0 | 1 | 4 | 6 | 4 | 1 | 0 | ... |
A kiterjesztés másik módja a másik átló egyeseit folytatja:
| m = −4 | m = −3 | m = −2 | m = −1 | m = 0 | m = 1 | m = 2 | m = 3 | m = 4 | m = 5 | ... | |
| n = −4 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... |
| n = −3 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | |
| n = −2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | ||
| n = −1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | ... | |||
| n = 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | ... |
| n = 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | ... |
| n = 2 | 0 | 0 | 0 | 0 | 1 | 2 | 1 | 0 | 0 | 0 | ... |
| n = 3 | 0 | 0 | 0 | 0 | 1 | 3 | 3 | 1 | 0 | 0 | ... |
| n = 4 | 0 | 0 | 0 | 0 | 1 | 4 | 6 | 4 | 1 | 0 | ... |
Újra a fenti szabállyal:
| m = −4 | m = −3 | m = −2 | m = −1 | m = 0 | m = 1 | m = 2 | m = 3 | m = 4 | m = 5 | ... | |
| n = −4 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... |
| n = −3 | −3 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... |
| n = −2 | 3 | −2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... |
| n = −1 | −1 | 1 | −1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | .. |
| n = 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | ... |
| n = 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | ... |
| n = 2 | 0 | 0 | 0 | 0 | 1 | 2 | 1 | 0 | 0 | 0 | ... |
| n = 3 | 0 | 0 | 0 | 0 | 1 | 3 | 3 | 1 | 0 | 0 | ... |
| n = 4 | 0 | 0 | 0 | 0 | 1 | 4 | 6 | 4 | 1 | 0 | ... |
Ez a kiterjesztés megőrzi a mátrixhatvány tulajdonságot, vagyis:
folytatása:
A kiterjesztés megőrzi a fent leírt Fibonacci-összeg tulajdonságot a negatív indexekre is.
Mindkét kiterjesztés értelmezhető a gammafüggvény felhasználásával:
és a gammafüggvény bizonyos határértékeit véve.
Történet[szerkesztés]

A binomiális együtthatók háromszögbe rendezésének legkorábbi ábrázolása a 10. században bukkant fel, a Chandas Shastra című ókori indiai könyvhöz írott kommentárokban. Az ókori szanszkrit nyelvű könyvet Pingala írta valamikor a Kr. e. 5. és 2. század között, de ez csak töredékesen maradt fenn. A könyvet kommentáló Halayudha 975 körül arra használta a háromszöget, hogy a Meru-prastaara-ra vagyis a Moru-hegy lépcsőire tett homályos utalásokat megmagyarázza. Arra is felfigyelt, hogy a „ferde” átlók tagjainak összege a Fibonacci-számokat adja. Később Bhattotpala indiai matematikus (1068 körül) megadta a háromszög sorait 0-tól 16-ig.
Ugyanebben az időben Perzsiában is tárgyalták Al-Karadzsi matematikus (953–1029) és Omar Khajjám költő-csillagász-matematikus (1048-1131); ezért a háromszöget Iránban „Khajjám-háromszög” néven ismerik. A háromszöghöz kapcsolódóan több tételt is ismertek, köztük a binomiális tételt.
A 13. században Yang Hui (1238-1298) bemutatta a számtani háromszöget, amely azonos volt a Pascal-háromszöggel. A háromszöget Kínában „Yang Hui-háromszög” néven ismerik.
Végül pedig Olaszországban „Tartaglia-háromszög” a neve, Niccolò Tartaglia matematikusról, aki egy évszázaddal Pascal előtt élt. Tartagliának tulajdonítják a harmadfokú egyenlet megoldását.
1655-ben Blaise Pascal a Traité du triangle arithmétique című értekezésében összegyűjtötte a háromszögre vonatkozó akkor ismert adatokat és valószínűségszámítási feladatok megoldására használta. A háromszöget utóbb Pierre Raymond de Montmort (1708) és Abraham de Moivre (1730) nevezte el Pascalról.
Kapcsolódó szócikkek[szerkesztés]
Hivatkozások[szerkesztés]
- ↑ [1]
- ↑ 'Pascal’s Triangle by Andrew Samuels. [2006. szeptember 18-i dátummal az eredetiből archiválva]. (Hozzáférés: 2007. július 20.)
- ↑ Negativ vagy n-nél nagyobb k esetében a binomiális együttható értékét nullának tekintjük.
- ↑ Brothers, H. J. (2012), "Finding e in Pascal’s triangle", Mathematics Magazine 85: 51, DOI 10.4169/math.mag.85.1.51.
- ↑ Brothers, H. J. (2012), "Pascal's triangle: The hidden stor-e", The Mathematical Gazette 96: 145–148.
- ↑ Fine, N. J. (1947), "Binomial coefficients modulo a prime", American Mathematical Monthly 54: 589–592, DOI 10.2307/2304500. See in particular Theorem 2, which gives a generalization of this fact for all prime moduli.
- ↑ Hasonló példa itt: Hore, P. J. (1983), "Solvent suppression in Fourier transform nuclear magnetic resonance", Journal of Magnetic Resonance 55 (2): 283–300, DOI 10.1016/0022-2364(83)90240-8.
- ↑ Karl, John H. (2012), An Introduction to Digital Signal Processing, Elsevier, p. 110, ISBN 9780323139595, <https://books.google.com/books?id=9Dv1PClLZWIC&pg=PA110>.
- ↑ Wolfram, S.. A New Kind of Science. Champaign IL: Wolfram Media, 870, 931–2. o. (2002)
Fordítás[szerkesztés]
Ez a szócikk részben vagy egészben a Pascal's triangle című angol Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.
Külső hivatkozások[szerkesztés]
Magyar[szerkesztés]
- A Pascal-háromszög szimmetriája, Kempelen Farkas Digitális Tankönyvtár
- A Pascal-háromszög néhány más tulajdonsága, Kempelen Farkas Digitális Tankönyvtár
Angol[szerkesztés]
- Weisstein, Eric W.: Pascal's triangle (angol nyelven). Wolfram MathWorld
- The Old Method Chart of the Seven Multiplying Squares (from the Ssu Yuan Yü Chien of Chu Shi-Chieh, 1303, depicting the first nine rows of Pascal's triangle)
- Pascal's Treatise on the Arithmetic Triangle (page images of Pascal's treatise, 1655; summary: [2])
- Earliest Known Uses of Some of the Words of Mathematics (P)
- Leibniz and Pascal triangles
- Dot Patterns, Pascal's Triangle, and Lucas' Theorem
- Pascal's Triangle From Top to Bottom
- Omar Khayyam the mathematician
- Info on Pascal's Triangle
- Explanation of Pascal's Triangle and common occurrences, including link to interactive version specifying # of rows to view























































![{\displaystyle \,{\mathfrak {Re}}\left({\text{Fourier}}\left[{\frac {\sin(x)^{5}}{x}}\right]\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7d4618708b6da830167e32a47559d936f29077b)
![{\displaystyle \,{\mathfrak {Re}}\left({\text{Fourier}}\left[{\frac {\sin(x)^{1}}{x}}\right]\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0bec81304674400f85993dbc174001dfd07e89f0)









