1 − 2 + 3 − 4 + · · ·

A matematikában az 1 − 2 + 3 − 4 + ··· egy végtelen alternáló sor, ami a pozitív egészekből áll váltakozó előjellel. Az első m tag összege:
Ez a sor divergens, vagyis parciális összegeinek nincs határértéke: (1, −1, 2, −2, ...). A 18. század közepén azonban Leonhard Euler ezt a paradox egyenlőséget írta fel:
Az egyenletet csak sokkal később sikerült matematikai pontossággal megérteni. Az 1890-es évektől Ernesto Cesàro, Émile Borel és mások jóldefinált módszereket gondoltak ki divergens sorok általánosított összegének meghatározására. Ezek közül több is az 1⁄4 általánosított összeget adta meg az 1 − 2 + 3 − 4 + ... sor esetén. Néhány módszer, például a Cesàro-összegzés nem konvergál, így megmutatja, hogy az összegzéshez szigorúbb módszer kell, például az Abel-szummáció.
Az 1 − 2 + 3 − 4 + · · · sor közel áll az 1 − 1 + 1 − 1 + ... Grandi-sorhoz. Euler ezek közös általánosításával foglalkozott; az 1 − 2n + 3n − 4n + ... sort vizsgálta. Ebből ered a bázeli probléma, ami elvezetett a függvényegyenletekhez, amiből a Dirichlet-féle éta-függvény és a Riemann-féle zéta-függvény is adódott.
Divergencia[szerkesztés]
Az (1, −2, 3, −4, ...) sorozat nem tart a nullához, emiatt az (1, −2, 3, −4, ...) sor divergál. Definíció szerint a sorok konvergenciáját részletösszegeik konvergenciája határozza meg, ám az (1, −2, 3, −4, ...) sor részletösszegei divergálnak:[1]
- 1 = 1,
- 1 − 2 = −1,
- 1 − 2 + 3 = 2,
- 1 − 2 + 3 − 4 = −2,
- 1 − 2 + 3 − 4 + 5 = 3,
- 1 − 2 + 3 − 4 + 5 − 6 = −3,
A részletösszegek sorozata minden pozitív és negatív egészt tartalmaz; ha a sor elejére odavesszük a nullát, akkor a nulla is, így minden egész előáll összegként, ezzel bizonyítva az egészek halmazának megszámlálhatóságát.[2] Ez a tulajdonság azt is mutatja, hogy a sorozatnak nincs határértéke, ugyanis minden javasolt x határértékre található olyan tagja a sornak, ami már az [x-1, x+1] intervallumon kívül esik, így 1 − 2 + 3 − 4 + ... divergál.
Az összegzés heurisztikái[szerkesztés]
Mivel az 1, −2, 3, −4, 5, −6, ... tagok egy egyszerű mintát követnek, ezért a sorozat könnyen kezelhető eltolással és összegzéssel. Ha van értelme annak, hogy s = 1 − 2 + 3 − 4 + ..., ahol s egy jól meghatározott szám, akkor a következő manipulációk szerint s = 1⁄4:[3]
Tehát s = 1⁄4.

Habár a szokásos értelemben az 1 − 2 + 3 − 4 + ..., sornak nincs összege, az s = 1 − 2 + 3 − 4 + ... = 1⁄4 egyenlet adja a legtermészetesebb választ, hogyha mégis definiálni szeretnénk ezt az összeget. Az összeg általánosítása divergens sorokra az összegzés vagy szummáció, ami bizonyos sorokra összeget definiál. Több módszer is létezik. A fenti manipuláció ezt bizonyítja: bármely lineáris és stabil összegzés az s = 1⁄4 összeget adja.[4] Továbbá, mivel
azért ezek a módszerek a Grandi-sorozatot is összegzik, és az összeg 1 − 1 + 1 − 1 + ... = 1⁄2.[4]
Cauchy-szorzat[szerkesztés]
1891-ben Ernesto Cesàro remélte, hogy a divergens sorozatok is matematikai pontossággal bevihetők az analízisbe: Azt állítják, hogy (1 − 1 + 1 − 1 + ...)2 = 1 − 2 + 3 − 4 + ..., és hogy mindkét oldal egyenlő 1⁄4-del.[5] Cesàro ezt egy előző évben megjelent tételének alkalmazásával kapta. Ez volt az első tétel az összegezhető divergens sorok elméletében. Ennek központi eleme az, hogy 1 − 2 + 3 − 4 + ... a 1 − 1 + 1 − 1 + ... és a 1 − 1 + 1 − 1 + ... Cauchy-szorzata.
Még a divergens sorok Cauchy-szorzata is definiálva van. Ekkor, ha Σan = Σbn = Σ(−1)n, akkor a Cauchy-szorzat tagjainak alakja
Ekkor a szorzatsor
Így ha egy módszer illeszkedik a Cauchy-szorzathoz, és az 1 − 1 + 1 − 1 + ... = 1⁄2 összeget adja, akkor szerinte 1 − 2 + 3 − 4 + ... = 1⁄4. Ebből következik, hogy 1 − 1 + 1 − 1 + ... és 1 − 2 + 3 − 4 + ... összegezhetősége ekvivalens a lineáris, stabil és a Cauchy-szorzathoz illeszkedő módszerek esetén, vagyis ha az egyik összegezhető, akkor a másik is.
A 1 − 1 + 1 − 1 + ... a leggyengébb értelemben Cesàro-összegezhető, azaz (C, 1)-összegezhető, viszont 1 − 2 + 3 − 4 + ... a Cesàro-tétel egy szigorúbb formáját igényli,[6] ezért (C, 2)-összegezhető. Mivel a Cesàro-tétel stabil és lineáris, ezért a korábban kiszámított összegeket adja.
Módszerek[szerkesztés]
Cesàro és Hölder[szerkesztés]

Az 1 − 2 + 3 − 4 + ..., esetleg létező (C, 1) Cesàro-összegéhez a részösszegek számtani összegei kellenek. A részösszegek:
- 1, −1, 2, −2, 3, −3, ...,
a számtani közepek:
- 1, 0, 2⁄3, 0, 3⁄5, 0, 4⁄7, ....
Ez a sorozat nem konvergens, így 1 − 2 + 3 − 4 + ... nem Cesàro-összegezhető.
A Cesàro-összegzésnek két általánosítását ismerjük, amelyek közül az egyszerűbb a (H, n) sorozat, ahol n természetes szám. A (H, 1) módszer maga a Cesàro-összegzés. A magasabb számú módszerek szintén a közepek sorozatán alapulnak. A sorozat párosadik közepei 1⁄2-hez tartanak, míg a páratlanadikok a konstans 0 sorozat. Így a közepek közepei 0 és 1⁄2 közepéhez tartanak, vagyis 1⁄4-hez.[7] Így 1 − 2 + 3 − 4 + ... (H, 2)-összegezhető, és összege 1⁄4.
Ebben a jelölésben H Otto Hölder tiszteletére szerepel, aki 1882-ben bebizonyította a kapcsolatot az Abel-összegzés és a (H, n) összegzések között. Első példája az 1 − 2 + 3 − 4 + ... volt.[8] Az a tény, hogy 1 − 2 + 3 − 4 + ... (H, 2)-összege 1⁄4, garantálja az Abel-összegezhetőséget, és hogy az Abel-összeg is ennyi.
A Cesàro-összegzés egy másik gyakori általánosítása a (C, n) sorozat. Tudjuk, hogy (C, n) és (H, n) mindig ugyanazt az eredményt adja, de történelmi háttere különböző. 1887-ben Cesàro már közel volt a (C, n) sorozat definiálásához, de mindig csak néhány példája volt. Valamelyik (C, n) módszerrel összegezte 1 − 2 + 3 − 4 + ...,-et az 1⁄4 eredménnyel. A pontos módszert nem publikálta. Csak 1890-ben formalizálta (C, n)-módszereket, hogy kimutassa: a (C, n)-összegezhető és a (C, m)-összegezhető sorok szorzata (C, m + n + 1)-összegezhető.[9]
Abel-összegzés[szerkesztés]

Egy 1749-es írásában Leonhard Euler megállapította, hogy a sor divergál, de mégis szeretett volna összeget rendelni hozzá:
Ha azt mondjuk, hogy 1−2+3−4+5−6 összege 1⁄4, akkor ez a kijelentés paradoxnak látszik. Az első 100 tag összege -50, az első 101 tagé azonban 51, ami elég messze van az 1⁄4-től, sőt, ez a különbség még tovább nő. De, ahogy azt már előbb megjegyeztem, az összeg szónak egy másik jelentést kell adni.[10]
Euler többször is javasolta az összeg általánosabb értelmezését. Az 1 − 2 + 3 − 4 + ... sor esetén ötlete az Abel-összegzésre hasonlít:
Többé nem lehet kétséges, hogy 1−2+3−4+5 + összege 1⁄4, mivel az 1⁄(1+1)2 képlet kifejtéséből keletkezik, aminek értéke cáfolhatatlanul 1⁄4. Az ötlet jobban felismerhető, ha az 1 − 2x + 3x2 − 4x3 + 5x4 − 6x5 + &c. generátorsort tekintjük, ami az 1⁄(1+x)2 kifejtése. Ebbe x = 1-et helyettesítve éppen a szóban forgó sorozatot kapjuk.[11]
Ez többféleképpen is belátható az |x| < 1 értékekre. Ekkor
Vehetjük a jobb oldal Taylor-sorfejtését, vagy formálisan a hosszú polinomosztást. Euler gondolatmenetét követve bal oldalról elindulva szorozhatunk kétszer (1+x)-szel, vagy vehetjük az 1 − x + x2 − .... mértani sor négyzetét. Euler a továbbiakban a tagonkénti deriválást sugallja.[12]
Mai fogalmaink szerint az 1 − 2x + 3x2 − 4x3 + ... sor nem definiál függvényértéket x = 1-ben, így az nem helyettesíthető be. Mivel azonban a függvény minden |x| < 1-re definiálva van, így vehetjük a határértéket, és ez már az Abel-szummáció:
Euler és Borel[szerkesztés]
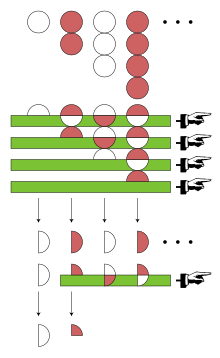
Euler egy másik módszerrel próbálkozott: az általa kidolgozott Euler-transzformációval. A transzformált kiszámításához először elhagyja az előjeleket az alternáló sorból, így jelen esetben 1, 2, 3, 4, .... a kiindulási sorozat. Ennek az első elemét a0-lal jelöljük.
A következőkben kiszámítjuk a differenciákat. Ez most 1, 1, 1, 1, ..... Ennek első elemét Δa0-lal jelöljük. Az Euler-transzformáció a magasabb rendű differenciáktól és az iterációktól is függ, de sorozatunk másodrendű differenciái az azonosan nulla sorozat.
Ezekkel az előkészületekkel az Euler-transzformált:
Ma ezt így mondjuk: 1 − 2 + 3 − 4 + ... Euler-összegezhető, és összege 1⁄4.
Az Euler-összegezhetőségből egy másik összegezhetőség is következik. Az 1 − 2 + 3 − 4 + ... sor felírjuk egy másik alakban:
aminek van egy mindenütt egyenletesen konvergens rokon sora:
Így 1 − 2 + 3 − 4 + ... Borel-összege:
A mérlegek elkülönítése[szerkesztés]
Saichev és Woyczyński az elméleti fizikából átvett elvek alapján jutott az 1 − 2 + 3 − 4 + ... = 1⁄4 következtetésre. A két általuk felhasznált elv az infinitezimális relaxáció és a mérlegek elkülönítése. Ezekkel az elvekkel a φ-szummációk egész családja definiálható, amelyek minden tagja az 1⁄4 összeget adja.
Ha φ(x) egy kétszer folytonosan differenciálható függvény (0, ∞)-en úgy, hogy φ(0) = 1 és φ(x) és xφ(x) határértéke +∞-ben nulla, akkor:[13]
Ez az Abel-összegzés általánosítása, ami szintén beletartozik ebbe a családba az φ(x) = exp(−x) paraméterrel. Az általánosítás belátható a tagok m szerinti párosításával és a kifejezés Riemann-integrállá való átalakításával. A Grandi-sorozat összegzésével az utóbbi lépés kiadja a középértéktételt, ami azonban a Taylor-tétel erősebb Lagrange-formáját igényli.
Általánosításai[szerkesztés]
Az 1 − 1 + 1 − 1 + ... háromszoros Cauchy-szorzata 1 − 3 + 6 − 10 + ..., ami a háromszögszámok alternáló sorozata. Ennek Abel- és Euler-összege 1⁄8.[14] A négyszeres Cauchy-összeg 1 − 4 + 10 − 20 + ..., a tetraéderszámok alternáló összege, melynek Abel-összege 1⁄16.
Egy másik általánosítás az 1 − 2n + 3n − 4n + ... n más értékeire. Pozitív egész n értékre ez az összeg adódik:[15]
ahol Bn Bernoulli-szám.
Páros n-ekre ez egyszerűsíthető:
Abel 1826-ban így írt erről: A divergens sorozatok az ördög művei, és szégyen, hogy vannak, akik bizonyításokban használják őket, ami sok boldogtalanságot és paradoxont okoz. Itt olyan szörnyűségre lehet gondolni, mint
- 0 = 1 − 2n + 3n − 4n + etc.
ahol n pozitív egész szám. Ez egy olyan dolog, amin inkább csak nevetni lehet.[16]
Cesàro tanárának, Eugène Charles Catalannak is kétségei voltak a divergens sorozatok összegzésével szemben, így Cesàro is nehezen tudta elfogadni ezeket a módszereket. Kezdetben abszurdnak nevezte az 1 − 2n + 3n − 4n + ... sorozatok összegzési képleteit. 1883-ban arról írt, hogy ezek a képletek ugyan nem igazak, de valami miatt formálisan működnek. Végül 1890-ben a Sur la multiplication des séries írásában a definíciókkal kezdődően már a modern felfogás szerint építette fel a divergens sorozatok összegzésének képleteit.[17]
A sorozatot n nem egész értékeire is vizsgálták, így a Dirichlet-féle éta-függvényhez jutottak. Euler részben az éta függvényből kiindulva tanulmányozta az 1 − 2 + 3 − 4 + ... sorozatot, így jutott a Riemann-féle zéta-függvény egyenletéig. Euler korábban már híressé vált arról, hogy páros számokra kiszámította ezeknek a függvényeknek az értékeit, beleértve a bázeli probléma megoldását. Megpróbálta a páratlan számokra is megtalálni ezeket a függvényértékeket, de ez a probléma máig megoldatlan maradt. Az éta függvény könnyebben kezelhető Euler eszközeivel, mivel Dirichlet-sora mindenütt Abel-összegezhető. A zéta függvény Dirichlet-sora nehezebben vizsgálható ott, ahol a függvény is divergál.[18] Így például 1 − 2 + 3 − 4 + ... megfelelője a nem alternáló 1 + 2 + 3 + 4 + ... sor, ami a modern fizikában is megjelenik, de erősebb eszközöket igényel az összegzéshez.
Jegyzetek[szerkesztés]
- ↑ Hardy p.8
- ↑ Beals p.23
- ↑ Hardy (p.6) ezt az átalakítást az 1 − 1 + 1 − 1 + ... Grandi-sorral végzi el.
- ↑ a b Hardy p.6
- ↑ Ferraro, p.130.
- ↑ Hardy, p.3; Weidlich, pp.52–55.
- ↑ Hardy, p.9. For the full details of the calculation, see Weidlich, pp.17–18.
- ↑ Ferraro, p.118; Tucciarone, p.10. Ferraro criticizes Tucciarone's explanation (p.7) of how Hölder himself thought of the general result, but the two authors' explanations of Hölder's treatment of 1 − 2 + 3 − 4 + ... are similar.
- ↑ Ferraro, pp.123–128.
- ↑ Euler et al., p.2. Habár ez a cikk 1749-ben íródott, csak 1768-ban jelent meg.
- ↑ Euler et al., pp.3, 25.
- ↑ For example, Lavine (p.23) advocates long division but does not carry it out; Vretblad (p.231) calculates the Cauchy product. Euler's advice is vague; see Euler et al., pp.3, 26. John Baez even suggests a category-theoretic method involving multiply pointed sets and the quantum harmonic oscillator. Baez, John C. Euler's Proof That 1 + 2 + 3 + ... =-1/12 (PDF). math.ucr.edu (December 19, 2003). Hozzáférés ideje: March 11, 2007.
- ↑ Saichev and Woyczyński, pp.260–264.
- ↑ Kline, p.313.
- ↑ Knopp, p.491; there appears to be an error at this point in Hardy, p.3.
- ↑ Grattan-Guinness, p.80. See Markushevich, p.48, for a different translation from the original French; the tone remains the same.
- ↑ Ferraro, pp.120–128.
- ↑ Euler et al., pp.20–25.
Források[szerkesztés]
- Beals, Richard. Analysis: an introduction. Cambridge UP (2004). ISBN 0-521-60047-2
- Davis, Harry F.. Fourier Series and Orthogonal Functions. Dover (1989. május 1.). ISBN 0-486-65973-9
- Euler, Leonhard; Lucas Willis; and Thomas J Osler: Translation with notes of Euler's paper: Remarks on a beautiful relation between direct as well as reciprocal power series. The Euler Archive, 2006. (Hozzáférés: 2007. március 22.) Originally published as Euler, Leonhard (1768). „Remarques sur un beau rapport entre les séries des puissances tant directes que réciproques”. Memoires de l'academie des sciences de Berlin 17, 83–106. o.
- Ferraro, Giovanni (1999. június 1.). „The First Modern Definition of the Sum of a Divergent Series: An Aspect of the Rise of 20th Century Mathematics”. Archive for History of Exact Sciences 54 (2), 101–135. o. DOI:10.1007/s004070050036.
- Grattan-Guinness, Ivor. The development of the foundations of mathematical analysis from Euler to Riemann. MIT Press (1970). ISBN 0-262-07034-0
- Hardy, G. H.. Divergent Series. Clarendon Press, xvi+396. o. (1949). ISBN 978-0-8218-2649-2. OCLC 808787 2nd Ed. published by Chelsea Pub. Co., 1991. LCCN 91075377. ISBN 0828403341.
- Kline, Morris (1983. november 1.). „Euler and Infinite Series”. Mathematics Magazine 56 (5), 307–314. o. DOI:10.2307/2690371.
- Lavine, Shaughan. Understanding the Infinite. Harvard UP (1994). ISBN 0-674-92096-1
- Markusevič, Aleksej Ivanovič. Series: fundamental concepts with historical exposition, English translation of 3rd revised edition (1961) in Russian, Delhi, India: Hindustan Pub. Corp., 176. o. (1967). OCLC 729238507 Author also known as A. I. Markushevich and Alekseï Ivanovitch Markouchevitch. Also published in Boston, Mass by Heath with OCLC 474456247. Additionally, OCLC 208730, OCLC 487226828.
- Saichev, A.I., and W.A. Woyczyński. Distributions in the physical and engineering sciences, Volume 1. Birkhaüser (1996). ISBN 0-8176-3924-1
- Tucciarone, John (1973. január 1.). „The development of the theory of summable divergent series from 1880 to 1925”. Archive for History of Exact Sciences 10 (1–2), 1–40. o. DOI:10.1007/BF00343405.
- Vretblad, Anders. Fourier Analysis and Its Applications. Springer (2003). ISBN 0-387-00836-5
- Weidlich, John E.. Summability methods for divergent series. Stanford M.S. theses (1950. június 1.). OCLC 38624384
Fordítás[szerkesztés]
- Ez a szócikk részben vagy egészben a(z) 1 − 2 + 3 − 4 + ⋯ című angol Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.




![{\displaystyle {\begin{array}{rclllll}4s&=&&(1-2+3-4+\cdots )&{}+(1-2+3-4+\cdots )&{}+(1-2+3-4+\cdots )&{}+(1-2+3-4+\cdots )\\&=&&(1-2+3-4+\cdots )&{}+1+(-2+3-4+5+\cdots )&{}+1+(-2+3-4+5+\cdots )&{}+(1-2)+(3-4+5-6\cdots )\\&=&&(1-2+3-4+\cdots )&{}+1+(-2+3-4+5+\cdots )&{}+1+(-2+3-4+5+\cdots )&{}-1+(3-4+5-6\cdots )\\&=&1+&(1-2+3-4+\cdots )&{}+(-2+3-4+5+\cdots )&{}+(-2+3-4+5+\cdots )&{}+(3-4+5-6\cdots )\\&=&1+[&(1-2-2+3)&{}+(-2+3+3-4)&{}+(3-4-4+5)&{}+(-4+5+5-6)+\cdots ]\\&=&1+[&0+0+0+0+\cdots ]\\4s&=&1\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/30a6576c86da4caf35766c0f081d6841fc017445)

![{\displaystyle {\begin{array}{rcl}c_{n}&=&\displaystyle \sum _{k=0}^{n}a_{k}b_{n-k}=\sum _{k=0}^{n}(-1)^{k}(-1)^{n-k}\\[1em]&=&\displaystyle \sum _{k=0}^{n}(-1)^{n}=(-1)^{n}(n+1).\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d43c146014f7b19d308aac55a97463246ebe5c9)









