Elektromos ellenállás
Elektromos ellenállásnak (pontosabban egyenáramú ellenállásnak, röviden ellenállásnak) nevezzük az elektromos vezető két pontjára kapcsolt feszültség és a vezetőn áthaladó áram erősségének a hányadosaként értelmezett fizikai mennyiséget. Jele a latin resistentia (=ellenállás) szó alapján R.
- , ahol a feszültség, az áramerősség.
Az ellenállás magyarázata[szerkesztés]
Az elektromos vezetőkben szabad töltéshordozók (elektronok, protonok, ionok stb.) vannak, amelyek a vezetőn belül rendezetlen hőmozgást végeznek. Ha a vezetőre feszültséget kapcsolunk, akkor a feszültség polaritása és a töltéshordozók töltésének előjele által meghatározott irányú rendezett mozgás jön létre. Az áramló töltéshordozók gyorsuló mozgást végeznek, és időnként kölcsönhatásba lépnek a vezető anyagát alkotó részecskékkel. A külső tér által végzett munka révén a gyorsuló töltéshordozók energiára tesznek szert. Ez az energia a kölcsönhatás során a vezető belső energiáját növeli, aminek ezzel együtt többnyire a hőmérséklete is növekszik. A töltéshordozók mozgását, azaz az elektromos áramot a vezető tehát kisebb-nagyobb mértékben akadályozza. A vezető ezen akadályozó tulajdonságát jellemezzük az egyenáramú ellenállással. Fentiekből érthetően az ellenállás függ a hőmérséklettől.
Váltóáramú hálózatokban az ellenállás szerepét a komplex impedancia (röviden impedancia) veszi át.
Az ellenállás mértékegysége[szerkesztés]
Az ellenállás SI-mértékegysége az ohm, jele: Ω. Nevét Georg Simon Ohm német fizikusról kapta.
Az ellenállás definíciójából adódóan:
- .
Az ohm az SI-alapegységekkel kifejezve:
- .
Az ellenállás gyakrabban használt további mértékegységeit az alábbi táblázat tartalmazza.
| Név | Jel | Értéke | |
|---|---|---|---|
| milliohm | mΩ | 10−3 Ω | 0,001 Ω |
| kiloohm | kΩ | 103 Ω | 1000 Ω |
| megaohm/megohm | MΩ | 106 Ω | 1 000 000 Ω |
| gigaohm | GΩ | 109 Ω | 1 000 000 000 Ω |
Elektromos vezetőképesség[szerkesztés]
Az ellenállás reciproka az elektromos vezetőképesség:
Mértékegysége: siemens (S , ), amit Ernst Werner von Siemens német feltalálóról neveztek el.
Huzalok ellenállása. A fajlagos ellenállás[szerkesztés]

A huzalok viszonylag hosszú, azonos keresztmetszetű és azonos anyagú vezetők. Kísérletekkel igazolható, hogy állandó hőmérsékleten adott anyagból készült huzalok ellenállása egyenesen arányos a huzal hosszával (), és fordítottan arányos a huzal keresztmetszetével ().
- ,
ahol a arányossági tényező az adott anyagra jellemző fajlagos ellenállás.
A fajlagos ellenállás SI-mértékegysége: ohm·méter, jele: Ω·m.
A gyakorlatban használják még az Ω·mm²/m egységet is.
A két mértékegység közti kapcsolat:
Az ellenállás hőmérsékletfüggése[szerkesztés]
A mérések szerint az ellenállás függ a hőmérséklettől. Melegítés hatására a fémek ellenállása általában növekszik, a grafit, a félvezetők, az elektrolitok ellenállása pedig általában csökken. Az ellenállás-változás jelentős része abból adódik, hogy a vezető fajlagos ellenállása függ a hőmérséklettől, a hőtágulásból eredő méretváltozások szerepe elhanyagolhatóan kicsi.
A fémes vezetők ellenállásának relatív megváltozása közönséges hőmérsékleteken, nem túl nagy tartományban (pl. 0 °C – 100 °C között) megközelítőleg egyenesen arányos a hőmérséklet-változással, azaz
- ,
ahol állandó az adott anyag adott hőmérséklet környékén mért ellenállás hőfoktényezője (vagy hőmérsékleti tényezője, röviden hőfoktényezője).
A fenti összefüggésből:
- .
A T0 kiindulási hőmérséklet többnyire 0 °C vagy 20 °C, az ehhez tartozó fajlagos ellenállást ρ0 jelöli. Az anyagok hőfoktényezőjének megadásakor meg kell adni, hogy az adatok milyen kiindulási hőmérsékletre vonatkoznak. A hőfoktényező SI-mértékegysége:
A hőmérséklet-változást a gyakorlatban többnyire Celsius-fokban mérjük, ezért a hőfoktényező másik mértékegysége:
Mivel a hőmérsékletváltozás mérőszáma a Celsius-skálán és a Kelvin-skálán mindig ugyanakkora, ezért a hőfoktényező fenti két mértékegysége is megegyezik. A hőfoktényező értelmezhető a fajlagos ellenállás hőmérsékletfüggése alapján is, azaz
- .
Könnyen belátható, hogy a két definíció egyenértékű egymással.
Az anyagok ellenállása elég alacsony hőmérsékleten a fentieknél bonyolultabban változik. Az ellenállás bizonyos fémeknél, illetve kerámiáknál az abszolút nulla fok (azaz 0 K) közelében gyakorlatilag nullává válik. Ezt a jelenséget szupravezetésnek, az ilyen anyagot szupravezetőnek nevezzük.
Egyenáramú hálózatok eredő ellenállása[szerkesztés]
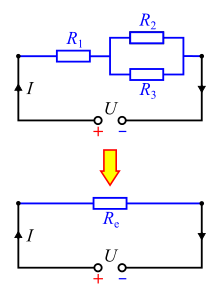
A gyakorlatban szükség lehet arra, hogy egymással összekapcsolt fogyasztókat egyetlen fogyasztóval helyettesítsünk úgy, hogy a hálózat többi részén ennek hatására semmiféle változás se történjen. Annak a fogyasztónak az ellenállását, amellyel a rendszer ilyen módon helyettesíthető, eredő ellenállásnak nevezzük. Jele többnyire Re, de ha nem okoz félreértést, egyszerűen csak R-rel jelöljük.
Soros kapcsolás[szerkesztés]

Fogyasztók soros kapcsolásánál az egyes fogyasztók elágazás nélkül kapcsolódnak egymáshoz. A rendszer két kivezetését az első és az utolsó fogyasztó szabadon maradó kivezetései alkotják. Mérésekkel, illetve elméleti úton is igazolható, hogy soros kapcsolásnál a rendszer eredő ellenállása ugyanakkora, mint az egyes fogyasztók ellenállásának összege. Képlettel:
Speciálisan n db R ellenállású fogyasztó soros kapcsolásánál az eredő ellenállás:
Párhuzamos kapcsolás[szerkesztés]

Fogyasztók párhuzamos kapcsolásánál minden fogyasztó egyik kivezetése a rendszer egyik kivezetéséhez, a másik vége pedig a rendszer másik kivezetéséhez csatlakozik. Mérésekkel, illetve elméleti úton is igazolható, hogy párhuzamos kapcsolásnál a rendszer eredő ellenállásának reciproka ugyanakkora, mint az egyes ellenállások reciprokának összege. Képlettel:
Speciálisan n db R ellenállású fogyasztó párhuzamos kapcsolásánál az eredő ellenállás:
Igazolható, hogy két fogyasztó párhuzamos kapcsolásánál az eredő ellenállás közvetlenül az
összefüggés alapján is kiszámítható.
Kapcsolódó szócikkek[szerkesztés]
- Impedancia
- Látszólagos ellenállás
- Hatásos ellenállás
- Meddő ellenállás
- Fajlagos ellenállás
- Elektromos vezetés
- Termisztor
- Ideális vezető
- Szupravezetés
Források[szerkesztés]
- Budó Ágoston: Kísérleti fizika II., Budapest, Tankönyvkiadó, 1971.
- ifj. Zátonyi Sándor: Fizika 10., Budapest, Nemzeti Tankönyvkiadó, 2009. ISBN 978 963 19 6320 5
További információk[szerkesztés]
- Fizikakönyv.hu – Ohm törvénye. Az ellenállás
- Fizikakönyv.hu – Fogyasztók kapcsolása
- Fizikakönyv.hu – A vezeték ellenállása




![{\displaystyle \left[R\right]={\frac {\left[U\right]}{\left[I\right]}}={\frac {\mbox{V}}{\mbox{A}}}=\Omega }](https://wikimedia.org/api/rest_v1/media/math/render/svg/141d38e13689c64048d5994b5216e27d35284bf8)












![{\displaystyle \left[\alpha \right]={\frac {\left[\rho -\rho _{0}\right]}{\left[\rho _{0}\right]\cdot \left[T-T_{0}\right]}}={\frac {\Omega \cdot \mathrm {m} }{\Omega \cdot \mathrm {m} \cdot \mathrm {K} }}={\frac {1}{\mathrm {K} }}=\mathrm {K} ^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/457451911ac8ab8eabca97b90cccb49486a500ed)
![{\displaystyle \left[\alpha \right]={\frac {1}{\mathrm {^{\circ }C} }}=(\mathrm {^{\circ }C} )^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73f76bba7d53527e180f830390a753b90b33b5d2)





