Egyenes
Az egyenes a pont és a sík mellett a geometria egyik alapfogalma. Leírása (és nem definíciója) szerint mindkét irányban végtelen, végtelenül keskeny vonal. Két pont közötti legrövidebb út szakasz.
A modern axiomatikus elméletekben az egyenes belső tulajdonságok nélküli objektum; csak a más egyenesekkel, pontokkal és síkokkal való kapcsolata érdekes.
Az analitikus geometriában az egyenes ponthalmaz. Pontosabban, az affin geometriában az egyenes egydimenziós altér.
Az egyenes definiálhatóságáról[szerkesztés]
Euklidész Kr. e. 300 körül megjelent művében, az Elemekben először a vonalat definiálta:
- „A vonal szélesség nélküli hosszúság”
és csak ezután következik az egyenes:
- „Egyenes vonal az, amelyik a rajta levő pontokhoz viszonyítva egyenlően fekszik.”[1]
Ez a megfogalmazás Eukleidész azon törekvéséből fakad, hogy mindent, amivel foglalkozik, pontosan meghatározzon, minden logikai rést lefedjen. Manapság az egyenest az elemi geometria axiomatikus tárgyalásában (például a Hilbert-féle axiómarendszerben) alapfogalomnak tekintjük, azaz nem vezetjük vissza további definícióval más fogalmakra.
Másrészt az elemi geometria modelljeiben természetesen meg kell adnunk az egyenesnek megfelelő entitások halmazát, például a koordinátamodellben mint egy háromdimenziós vektortér egydimenziós altereinek eltoltjainak halmazát.
Tulajdonságai[szerkesztés]
Habár nincs definiálva, mindenkiben él egy kép az egyenesről, amely szerint az egyenes egy pontokból álló 1 dimenziós objektum, azaz például a tér egy irányában végtelen hosszú, a többiben kiterjedés nélküli. A geometriában az egyenes következő tulajdonságait használjuk ki:
- Két pont egyértelműen meghatároz egy egyenest, amiből következik, hogy két különböző egyenesnek nem lehet egynél több közös pontja.
- Ha egy síknak és egy egyenesnek legalább két közös pontja van, akkor az egyenes illeszkedik az adott síkra.
- Ha egy egyenes pontjai és az és pontok között fekszik, akkor egyszersmind a pont a és pontok között is fekszik.
- Ha egy egyenes pontjai, akkor létezik olyan pontja az egyenesnek, amely az és pontok között fekszik, és egyszersmind létezik olyan pontja, hogy a pont az és pontok között is fekszik.
- Az egyenes tetszőleges három pontja közül pontosan egy olyan pont van, amely a másik két pont között fekszik.
A projektív geometriában él a dualitás tétele (egyes rendszerek szerint axiómája). Ez egy szimmetriaelv, hogy ha egy dimenziós térben állítunk valamit a dimenziós és az dimenziós alterek illeszkedési tulajdonságairól, akkor az állítás igazságtartalma megmarad, ha a dimenziós alterek helyett , az dimenziós altereket dimenziósakra cseréljük, az illeszkedési relációt pedig megtartjuk. Speciálisan, projektív síkokon az egyenesek és pontok duálisak. Így projektív síkokon képzelhető a pont végtelen hosszúnak, és az egyenes minden irányból végtelenül kicsinek. Három dimenziós projektív terekben a pontok és a síkok duálisak egymással, az egyenesek pedig egyenesekkel duálisak.
Egyenes megadása az analitikus geometriában[szerkesztés]
Az analitikus geometriában a geometriai tér egy -dimenziós vektortér a valós számok felett. Az egyenes egydimenziós affin altér, azaz egy -1 dimenziós lineáris altér mellékosztálya.
Három dimenzióban az analitikus geometria eleget tesz a Hilbert-féle axiómarendszernek; így az analitikus geometria egyenesei megfelelnek a Hilbert-féle axiómarendszereinek.
- Egy egyenes egyenlete
- olyan egyenlet, melyet az egyenes minden pontja teljesít, és ha egy pont teljesíti, akkor rajta van az egyenesen.
- A síkban az egyenes egyenletének általában háromféle alakját használjuk (Descartes-féle koordináta-rendszerben):
- Ha adott az egyenes egy pontja és egy normálvektora:[2] .[3]
- Ha az egyenesnek egy pontja és a meredeksége (vagy iránytangense)[4] adott: , ahol a b konstansra teljesül.
- Adva legyen az egyenes pontja, és az tengellyek bezárt szöge, . Ha az egyenes nem függőleges, akkor egyenlete . Ha függőleges, akkor egyenlete .
- Ha adott az egyenes két pontja és , akkor az egyenes bármely pontja meghatározható az összefüggés szerint.
- Legyenek , az egyenes különböző pontjai. Ekkor az egyenes pontjaira teljesül, hogy ahol , így az egyenes egyenlete .
- A térben már kevésbé szép, ekkor egyenletrendszerekkel írhatjuk le:
- Ha adott az egyenes egy pontja és egy irányvektora:[5] , ahol a t valós paraméter.
- Kicsit átalakítva az előző egyenletrendszert (amennyiben , azaz az irányvektor egyik koordinátája sem 0, nem párhuzamos egyik koordináta-tengellyel sem):
- Az n dimenziós térben az egyenest egy n változós egyenletrendszer adja meg, amiben van egy független paraméter
- Legyen helyvektor, irányvektor. Ekkor a ponton átmenő irányú egyenes egyenlete:
- .
- Legyenek helyvektorok úgy, hogy . Ekkor egyértelműen létezik egy egyenes, ami mindkettőre illeszkedik, és egyenlete:
- .
Két különböző vektor affin burka egyenes:
- , ahol , a vektorok.
Egyenesek kölcsönös helyzete[szerkesztés]
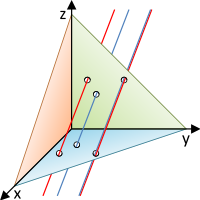
- Egyenesek kölcsönös helyzete (pirossal és kékkel) a térben
-
valódi párhuzamosság (balra) és egybeesés (jobbra)
-
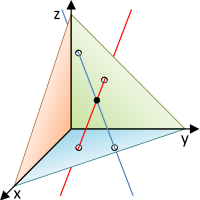
metsző (a fekete pontban)
-
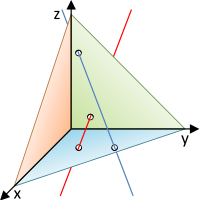
kitérő
- Párhuzamosság: A két egyenes eltolással átvihető egymásba. A párhuzamosság ekvivalenciareláció.
- Egybeesés: A két egyenes összes pontja ugyanaz, azaz ponthalmazként megegyeznek. Nullvektorral való eltolással vihetők egymásba-
- Valódi párhuzamosság: A két egyenes nem esik egybe, de irányuk megegyezik. Nullvektortól különböző vektorral való eltolással átvihetők egymásba.
- Metszők: Az egyeneseknek egy közös pontja van.
- Kitérők: Az egyeneseknek nincs közös pontjuk, és nem vihetők eltolással egymásba. Csak legalább háromdimenziós térben lehetséges.
Metszéspont a síkban[szerkesztés]

A síkban két, egyenlettel adott, metsző egyenes metszéspontjának számításához a Cramer-szabály nyújt segítséget:
Ha , akkor az egyenesek párhuzamosak.
Ha az egyenesek két-két pontjukkal adottak, azaz az első egyenes a és pontokkal, a második pedig a és pontokkal, akkor ki kell számítani az egyenesek egyenleteit. Így az metszéspontra adódik, hogy
- és
- .
Szemben az egyenesekkel, a síkban a nem párhuzamos szakaszok nem feltétlenül metszik egymást. Legyen a két szakasz és . Ekkor a szakaszok paraméteres egyenlettel írhatók le:
- ,
ahol . Ha létezik az metszéspont, akkor vannak olyan paraméterek, hogy
Ahogy a fenti esetben, úgy most is a Cramer-szabály segít nekünk. Ezután még azt is vizsgálnunk kell, hogy . Ha ez teljesül, akkor a paraméterek behelyettesítésével megkapjuk a szakaszok metszéspontjának koordinátáit.
Legyenek például a szakaszok és . Ekkor az egyenletrendszer
így , és a szakaszok metszik egymást. A metszéspont koordinátái .
Két ponttal adott egyenesek metszéspontja is számítható ugyanígy, ám ekkor nem kell vizsgálni, hogy .
Egyenesek szöge a síkban[szerkesztés]
Ha egy egyenes egyenlete formában adott, akkor irányszögére, -ra teljesül, hogy:
- ,
ami következik a tangens definíciójából. Alkalmazva a tangens inverz függvényét, az árkusz tangenst:
Ha ezek az egyenletek nincsenek definiálva, akkor , az egyenes függőleges. A tangensfüggvénynek pólusa van a és az helyen.[6]
Legyenek és a egyenesek a síkban, és legyenek adva az és egyenletekkel adva úgy, hogy és helyvektorok, és és lineárisan független irányvektorok! Ekkor a két egyenes által bezárt szögre teljesül, hogy:
Az egyenesek merőlegesek, más szóval, ortogonálisak akkor, ha derékszöget zárnak be, azaz . Ez pontosan akkor teljesül, ha az irányvektorok skaláris szorzata nulla, azaz .[7]
Ha az egyenesek egyenlete és alakban adott, akkor az általuk közrezárt szög, irányszögeik különbsége:
A tangensfüggvény addíciós tételeivel:
Mivel és , következik, hogy:
Végeredményben
Alkalmazva a tangens inverz függvényét kapjuk, hogy:
Az egyenesek pontosan akkor merőlegesek, ha a nevező nulla, azaz . Ekkor a fenti egyenletek nincsenek értelmezve, mivel a tangensfüggvénynek pólusa van a és az helyen.[6]
Távolságok a síkban[szerkesztés]
Adva legyen a pont, és az egyenletű egyenes. Távolságuk:
Az egyenes ponthoz legközelebbi pontjának koordinátái:
Ha az egyenes két pontjával van adva, akkor alakú egyenletének együtthatói:
és ezek az együtthatók helyettesíthetők be a képletekbe.[8]
Távolságok a térben[szerkesztés]
A pont és az , illetve pontokon átmenő egyenes távolsága: [9]
Ha az egyik egyenes a és pontokon, a másik a és pontokon halad át, akkor távolságuk:[10]
Lásd még[szerkesztés]
Hivatkozások[szerkesztés]
- David Hilbert: Grundlagen der Geometrie, B.G. Taubner, Leizig, 2. kiadás, 1903
- Hajós György: Bevezetés a geometriába, Nemzeti Tankönyvkiadó, Budapest, 10. kiadás, 1994, ISBN 963-18-5622-4
- Strommer Gyula: Geometria, Nemzeti Tankönyvkiadó, Budapest, 2. kiadás, 1993, ISBN 963-18-5312-8
Források[szerkesztés]
- Line szócikk a MathWorld lapján
- Euklidész: Elemek görögül és angolul
- Euklidész: Elemek 1. könyv magyarul
Jegyzetek[szerkesztés]
- ↑ Mayer Gyula fordításában
- ↑ Olyan vektor, ami merőleges az egyenesre
- ↑ Gyakran felteszik, hogy a normálvektor egység hosszú, azaz . Ez elsősorban kényelmi szempont, mert ekkor sok számítás leegyszerűsödik.
- ↑ Az egyenes és az x-tengely pozitív fele által bezárt szög (irányszög) tangense. Más megközelítésből: azt mondja meg, hogy az egyenes mennyit halad felfelé (negatív érték esetén lefelé), amíg 1-et megy jobbra. Függőleges egyeneseknél nincs értelmezve.
- ↑ Olyan vektor, ami párhuzamos az egyenessel
- ↑ a b Math Open Reference: Inverse tangent function (arctan)
- ↑ W3spoint.com: Angle between two lines Archiválva 2021. június 24-i dátummal a Wayback Machine-ben
- ↑ Wolfram MathWorld: Point-Line Distance--2-Dimensional
- ↑ Wolfram MathWorld: Point-Line Distance--3-Dimensional
- ↑ Wolfram MathWorld: Line-Line Distance
Fordítás[szerkesztés]
Ez a szócikk részben vagy egészben a Gerade című német Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.