Termodinamikai munka
A termodinamika I. főtételében szereplő munka fogalma alatt különböző fizika jellegű munkákat értünk, mint például az elektromos munka, a felületnöveléssel, az elegyítéssel járó munka stb. Ezek közé tartozik a termodinamikai munka (vagy térfogati munka) is, amely nem csak fizikai változások esetén, hanem a gyakran kémiai reakció lejátszódásakor is szükségszerűen fellép.
A fogalom kifejtése
[szerkesztés]Ha egy rendszerben – amelyben p nyomás uralkodik – bármilyen halmazállapotú anyagnak megnő a térfogata, a nyomás ellenében munkát kell végeznie, vagy ha csökken a térfogata, akkor a külső nyomás végez munkát. Ezt a munkát nevezzük térfogati munkának.

A munka az elmozdulásnak (ds) és az erőnek (F) az elmozdulás irányába eső vetületének a szorzata. Egy dugattyúval elzárt, V térfogatú tökéletes gáz térfogatváltozása során fellépő térfogati munka értelmezését mutatja a jobb oldali ábra. Az A felületű dugattyúra p külső nyomás hat, aminek hatására a dugattyú ds távolságra elmozdul, és ez dV = Ads térfogatváltozást okoz. Az állapotváltozás során végzett elemi munka:
A negatív előjel onnét származik, hogy megállapodás szerint a munka akkor pozitív, ha a külső erő végzi a rendszeren a munkát, vagyis ha a térfogat csökken. A δ jel arra utal, hogy a munka nem csak a térfogatváltozás nagyságától függ, hanem a munkavégzés körülményeitől is. Pl.: ugyanakkora ΔV térfogatváltozás esetén más-más nagyságú lesz a munka számszerű értéke, ha a folyamat során a nyomás állandó, vagy a hőmérséklet állandó. Ez azt jelenti, hogy a munka nem állapotfüggvény.
A fenti kifejezésből véges változásra vonatkozó térfogati munkát a V1 kezdeti és a változás végén betöltött V2 térfogat közötti integrálással számíthatjuk ki:
A számításhoz meg kell adni, hogy milyen feltételek között történik a munkavégzés, azaz milyen az állapotváltozás. Példaként az alábbiakban tökéletes gázt választunk, mert erre egzakt összefüggések ismeretesek.
Izoterm állapotváltozás
[szerkesztés]Izoterm állapotváltozás során
- T (hőmérséklet) konstans, ezért annak megváltozása 0.

Ha a hőmérséklet állandó, a belső energia is állandó, vagyis dU = 0, az I. főtétel alapján a rendszerrel közölt, vagy a rendszer által leadott hőmennyiség teljes mennyisége térfogat-növekedésre fordítódik, vagy a térfogatcsökkenésből származik, vagyis
és
Az ideális gáz állapotegyenletéből:
A Boyle–Mariotte-törvény alapján:
Behelyettesítés és integrálás után a gázon végzett térfogati munka:
Adiabatikus állapotváltozás
[szerkesztés]A környezetétől termikusan elszigetelt rendszer állapotváltozását adiabatikus állapotváltozásnak nevezzük, melyben
azaz a rendszer és a környezet között semmilyen hőcsere sem lehetséges. A termodinamika I. főtétele alapján és az állandó térfogaton vett moláris hőkapacitás definíció összefüggését felhasználva:

Véges változás esetén 1 mol tökéletes gáz adiabatikus térfogati munkája:
A kifejezésből – gyakorlatban tapasztaltakkal megegyezően – azt a következtetést lehet levonni, hogy az adiabatikusan összenyomott gáz fölmelegszik (pl.: a biciklipumpa, a dízelmotorok működése stb.), adiabatikusan kitáguló pedig lehűl. (lásd a kiszúrt szódavizes patron jegesedése, gázok cseppfolyósítása stb.).
Felhasználva a tökéletes gázok állandó nyomáson és állandó térfogaton mért moláris hőkapacitás közötti
összefüggést, valamint az adiabatikus kitevő definíció egyenletét:
az adiabatikus térfogati munka az alábbi módon is kiszámítható:
Kiindulva a
összefüggésből, és behelyettesítve az általános gáztörvényből a nyomás
kifejezését, az állapotjelzők közötti Poisson-egyenletekhez juthatunk.
A termodinamika Poisson-egyenletei
[szerkesztés]Ehhez a behelyettesítés és rendezés után kapott
differenciálegyenletet kell integrálni. Integrálás után az egyik Poisson-egyenletet kapjuk:
Az általános gáztörvényből T-t kifejezve és behelyettesítve, a
egy másik Poisson-egyenletet kapunk , ami az adiabata egyenlete. Kisebb átalakítás után a harmadik Poisson-egyenlethez juthatunk:
Politróp állapotváltozás
[szerkesztés]
Adiabatikus folyamatot szigorúan véve a gyakorlatban nem lehet megvalósítani, mert a rendszer tökéletesen nem szigetelhető el a környezetétől. Úgyszintén nem létezik tökéletesen izoterm folyamat sem. A gyakorlatban végbemenő folyamatot politrópnak nevezzük és a két állapotváltozás „között” zajlik, ennek megfelelően a politrópa egyenlete:
amelyben
vagyis a politrópa az izoterma és az adiabata „között” halad. A politróp változás során végzett térfogati munka – az adiabatikushoz hasonló tipusú – összefüggéssel számítható:
Izochor állapotváltozás
[szerkesztés]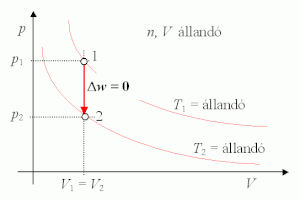
Izochor állapotváltozás során a rendszer térfogata állandó:
- dV = 0,
vagyis:
Tehát izochor állapotváltozás során nincs térfogati munka. A rendszerrel közölt hő a rendszer belső energiájának növelésére fordítódik, vagy a rendszer által leadott hő a belső energia csökkenéséből származik:
Izobár állapotváltozás
[szerkesztés]
Az izobár állapotváltozás során a nyomás állandó:
- dp = 0,
vagyis az integrálás egyszerűen elvégezhető:
Ha tehát állandó nyomáson növeljük a rendszer hőmérsékletét, akkor a térfogata nő, a rendszer munkát végez a környezetén, vagy fordítva, a hőmérséklet csökkentése esetén a környezet végez a rendszeren munkát.
Jegyzetek
[szerkesztés]Források
[szerkesztés]- Vitéz Gábor: FIZIKA I. Mechanika, Hőtan. (egyetemi jegyzet) Ideális gáz speciális állapotváltozásai., Miskolci Egyetem, Fizikai Tanszék
- Baranyai András: A termodinamika I. főtétele, ELTE Fizikai Kémiai Tanszék
- Alkalmazott fizika (távoktatási anyag) A hőtan első főtétele. Energia, energiatranszport. Pécsi Tudományegyetem, Fizikai Intézet, 2005
- Zajáczné Kovács Margit: Ideális gázok törvényei, Csány László Közgazdasági Szakközépiskola, Zalaegerszeg[halott link]


























