MATLAB
| MATLAB | |
 | |
 | |
| Fejlesztő | The MathWorks |
| Legfrissebb stabil kiadás | R2023b Update 6 (stabil verzió, 2024. január 10.) |
| Programozási nyelv | C, Java |
| Operációs rendszer | Platform független |
| Kategória | Numerikus matematikai szoftver |
| Licenc | kereskedelmi |
| A MATLAB weboldala | |
A MATLAB numerikus számítások elvégzésére alkalmas speciális programrendszer és egyben programozási nyelv amelyet A MathWorks fejleszt. A programrendszer képes mátrix számítások elvégzésére, függvények és adatok ábrázolására, algoritmusok implementációjára és felhasználói interfészek kialakítására. Habár a szoftver kizárólag numerikus, a MuPAD csomag hozzáadásával képes matematikai kifejezéseket grafikusan is megjeleníteni.
2004-ben, hivatalos információk alapján, a MATLAB több mint 1 millió felhasználóval rendelkezett.[1]
Történelem[szerkesztés]
A MATLAB-ot (jelentése: „matrix laboratory”) az 1970-es évek elején Cleve Moler kezdte el fejleszteni, az akkori Új-Mexikói Egyetem Számítástudományi Intézetének elnöke.[2] Kezdetben csak a diákjai munkáját tervezte megkönnyíteni, hogy ezen keresztül el tudják érni a LINPACK és EISPACK csomagokat Fortran tudás nélkül. Hamarosan elterjedt más egyetemek hallgatói és munkatársai között is és így erős érdeklődésre tett szert az alkalmazott matematikával foglalkozók körében. Jack Little, egy mérnök, Molernél tett látogatása során felismerte a MATLAB-ban lévő lehetőségeket 1983-ban. Utána nem sokkal csatlakozott Molerhez és Steve Bangert-hez, majd újraírták a MATLAB-ot C nyelven és megalapították a The MathWorks-öt 1984-ben. Ezek az újraírt könyvtárak JACKPAC néven váltak ismertté. 2000-ben a MATLAB-ot ismét újraírták, hogy alkalmas legyen az akkoriban született LAPACK programkönyvtár használatára.[3]
A MATLAB-ot először az irányítástechnikában alkalmazták, ami Little szakterülete is volt, de gyorsan elterjedt más területeken is. Manapság szintén használatos még az oktatásban, különösen a lineáris algebra és numerikus analízis szemléltetésében és népszerű még a képfeldolgozással foglalkozó kutatók között is.[2]
A MATLAB nyelv[szerkesztés]
Az egész MATLAB programrendszer a MATLAB nyelv köré épül, amit néha M-code-nak vagy egyszerűen M-nek hívnak. A legegyszerűbb módja az M-code fordításának az, hogy a fordítandó programot begépeljük a >> prompt után a Command Windowban, ami a MATLAB felület része. Ebben az esetben a MATLAB egy interaktív környezetként fog működni. Ha az M-code több sorból áll, érdemes a MATLAB Editort használni, amivel akár saját függvényt is készíthetünk.[4]
Változók[szerkesztés]
Változókat az értékadó operátorral lehet deklarálni, ami az =. A MATLAB egy dinamikusan típusos nyelv, ami azt jelenti, hogy a változókat típusdeklaráció nélkül is lehet használni, kivéve, ha szimbolikus objektumnak szánjuk őket.[5] A változók az értékeiket kaphatják konstansokból, számításokból, vagy egy függvény visszatérési értékéből is. Például:
>> x = 17
x =
17
>> x = 'hat'
x =
hat
>> x = [3*4, pi/2]
x =
12.0000 1.5708
>> y = 3*sin(x)
y =
-1.6097 3.0000
Mátrixok, vektorok[szerkesztés]
A MATLAB egy „Mátrix Laboratórium”, így többféle kényelmes megadási módját kínálja a vektoroknak, mátrixoknak és többdimenziós tömböknek.
A tömböket ciklus használata nélkül is fel lehet tölteni az alábbi szintaxissal: mettől:mennyivel:meddig. Például:
>> array = 1:2:9
array =
1 3 5 7 9
A fenti példa egy array nevű egydimenziós tömb változót deklarál, amely az 1, 3, 5, 7 és 9 értékeket tartalmazza. Ezzel a megadással a tömb elemei gyakorlatilag egy számtani sorozatot fognak képezni, amelynek első eleme a szintaxis első részében megadott mettől lesz, az utolsó eleme a szintaxis utolsó részében megadott meddig és a differencia pedig a középen álló mennyivel.
Ha a meddig nem tagja a sorozatnak, akkor a legnagyobb tag a nála kisebb számok közül az a szám lesz, amelyben mennyivel a legtöbbször megvan. Például:
>> array = 1:3:9
array =
1 4 7
A mennyivel értékét nem kötelező megadni, ha ezt elhagyjuk, akkor az értéke alapértelmezetten 1 lesz. Például:
>> array = 1:5
array =
1 2 3 4 5
Így az array nevű egydimenziós tömb értékei rendre az 1, 2, 3, 4 és 5 lesz.
A MATLAB nyelvben, ahogy a matematikában is, a tömbök és mátrixok indexelése 1-től kezdődik.[6] A legtöbb programozási nyelvben ez leggyakrabban 0-tól történik. A mátrixokat az elemek felsorolásával is meg lehet adni, szóközzel vagy vesszővel elválasztva úgy, hogy a listát szögletes zárójelek ([]) között helyezzük el. A pontosvessző azt jelenti a felsorolásban, hogy az utána álló elemek a következő sorba kerüljenek.[7] A kerek zárójelek használatával al-mátrixok is megjeleníthetőek. Például:
>> A = [16 3 2 13; 5 10 11 8; 9 6 7 12; 4 15 14 1]
A =
16 3 2 13
5 10 11 8
9 6 7 12
4 15 14 1
>> A(2,3)
ans =
11
>> A(2:4,3:4)
ans =
11 8
7 12
14 1
Négyzetes (-es) egységmátrix az eye[8] függvény használatával generálható. A zeros[9] és ones[10] függvények pedig -es mátrixokat töltenek fel 0-kkal és 1-esekkel.
>> eye(3)
ans =
1 0 0
0 1 0
0 0 1
>> zeros(2,3)
ans =
0 0 0
0 0 0
>> ones(2,3)
ans =
1 1 1
1 1 1
Pontosvessző[szerkesztés]
Más programozási nyelvekkel ellentétben, ahol a pontosvessző (;) választja el egymástól a parancsokat, a Matlabban, a parancsok kiírása függ tőle. Ha egy parancs végén pontosvessző szerepel, akkor nem kerül kiíratásra. Ellenkező esetben kiíródik. Ha egy parancs vagy függvény nem rendelkezik visszatérési értékkel, akkor ugyanaz történik a pontosvessző megléte vagy hiánya esetén is.
Grafika[szerkesztés]
A plot[11] függvény segítségével 2 dimenzióban ábrázolhatunk függvényeket, ahol az x tömb tartalmazza a megjelenítendő tartományt, az y tömb pedig a függvényt. Például:
x = 0:pi/100:2*pi;
y = sin(x);
plot(x,y)
Ez a kód az alábbi szinuszfüggvényt generálja:
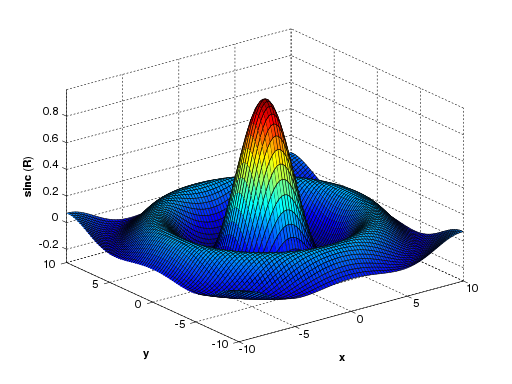
3 dimenziós függvényeket a surf,[12] plot3[13] és mesh[14] függvényekkel lehet megjeleníteni:
Verziók[15][szerkesztés]
| Verzió | Kódnév | Megjelenés ideje |
|---|---|---|
| MATLAB 1.0 | 1984 | |
| MATLAB 2 | 1986 | |
| MATLAB 3 | 1987 | |
| MATLAB 3.5 | 1990 | |
| MATLAB 4 | 1992 | |
| MATLAB 4.2c | R7 | 1994 |
| MATLAB 5.0 | R8 | 1996 |
| MATLAB 5.1 | R9 | 1997 |
| MATLAB 5.1.1 | R9.1 | |
| MATLAB 5.2 | R10 | 1998 |
| MATLAB 5.2.1 | R10.1 | |
| MATLAB 5.3 | R11 | 1999 |
| MATLAB 5.3.1 | R11.1 | |
| MATLAB 6.0 | R12 | 2000 |
| MATLAB 6.1 | R12.1 | 2001 |
| MATLAB 6.5 | R13 | 2002 |
| MATLAB 6.5.1 | R13SP1 | 2003 |
| MATLAB 6.5.2 | R13SP2 | |
| MATLAB 7 | R14 | 2004 |
| MATLAB 7.0.1 | R14SP1 | |
| MATLAB 7.0.4 | R14SP2 | 2005 |
| MATLAB 7.1 | R14SP3 | |
| MATLAB 7.2 | R2006a | 2006 |
| MATLAB 7.3 | R2006b | |
| MATLAB 7.4 | R2007a | 2007 |
| MATLAB 7.5 | R2007b | |
| MATLAB 7.6 | R2008a | 2008 |
| MATLAB 7.7 | R2008b | |
| MATLAB 7.8 | R2009a | 2009 |
| MATLAB 7.9 | R2009b | |
| MATLAB 7.9.1 | R2009bSP1 | 2010 |
| MATLAB 7.10 | R2010a | |
| MATLAB 7.11 | R2010b | |
| MATLAB 7.11.1 | R2010bSP1 | 2011 |
| MATLAB 7.12 | R2011a | |
| MATLAB 7.13 | R2011b | |
| MATLAB 7.14 | R2012a | 2012 |
| MATLAB 7.14 | R2012b | |
| MATLAB 9.12.0 | R2022a | 2012. március 9. |
| MATLAB 9.13 | R2022b | 2022. szeptember 15. |
Fordítás[szerkesztés]
- Ez a szócikk részben vagy egészben a MATLAB című angol Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.
Jegyzetek[szerkesztés]
- ↑ Richard Goering, "Matlab edges closer to electronic design automation world Archiválva 2007. szeptember 29-i dátummal a Wayback Machine-ben," EE Times, 10/04/2004
- ↑ a b Cleve Moler, a MATLAB készítője: The Origins of MATLAB, 2004. December. [2006. március 18-i dátummal az eredetiből archiválva]. (Hozzáférés: 2007. április 15.)
- ↑ Megjegyezés Cleve Molertől a Matlab készítőjétől MATLAB Incorporates LAPACK, 2000. (Hozzáférés: 2018. február 1.)
- ↑ MATLAB technikai dokumentáció. [2009. február 28-i dátummal az eredetiből archiválva]. (Hozzáférés: 2009. március 28.)
- ↑ A szimbolikus változókról Archiválva 2009. március 3-i dátummal a Wayback Machine-ben Dokumentáció a MATLAB Symbolic Toolbox-hoz
- ↑ A tömbök indexeléséről
- ↑ MATLAB dokumentáció a mátrixokról
- ↑ Az eye függvény MATLAB referenciája
- ↑ A zeros függvény MATLAB referenciája
- ↑ A ones függvény MATLAB referenciája
- ↑ A plot függvény MATLAB dokumentációja
- ↑ A surf függvény MATLAB dokumentációja
- ↑ A plot3 függvény MATLAB dokumentációja
- ↑ A mesh függvény MATLAB dokumentációja
- ↑ Cleve Moler: The Growth of MATLAB and The MathWorks over Two Decades (PDF), 2006. January. [2011. szeptember 19-i dátummal az eredetiből archiválva]. (Hozzáférés: 2008. augusztus 18.)
Külső hivatkozások[szerkesztés]
- Hivatalos blog
- MATLAB áttekintés, a The MathWorks oldaláról