Képlékenységtan

A képlékenységtan a képlékenyen alakítható anyagok, jellemzően a fémek képlékeny alakváltozásainak a törvényszerűségével és azok elméleti megfogalmazásával foglalkozó tudományág. Fontos feladata még az elméleti megfontolásoknak a gyakorlati alakítástechnológiai viszonyokra való alkalmazása is.
A fémből készült alkatrészekben és szerkezetekben a terhelés hatására mechanikai feszültségek és alakváltozások jönnek létre. A terhelés kezdeti szakaszában általában a Hooke-féle rugalmassági viszonyokat tekinthetjük érvényesnek (noha elméleti síkon ez is közelítésnek tekinthető, mert a valóságos anyagok nem az idealizált testek viselkedését követik), mikoris a feszültség és az alakváltozás jellege lineáris összefüggést követ. Ezt nevezzük rugalmas alakváltozási szakasznak. A terhelés további növekedésekor a képlékeny testekben kialakul egy olyan feszültség, amikor ez a jelleg eltér a lineáristól, az alakváltozás mértéke mintegy „meglódul” a feszültséghez képest. Az alakváltozásnak ez a szakasza a maradó vagy képlékeny alakváltozás tartománya. A rugalmas és a maradó alakváltozás között a különbséget a visszafordíthatóságban lehet megfogalmazni: a rugalmas alakváltozási szakaszban a terhelés megszűnése után a darab visszanyeri kiinduló méretét, alakját, míg a maradó alakváltozási szakaszban nincs meg ez a „visszaállás”, a képlékeny alakváltozásra tehát az irreverzibilitás jellemző.
A rugalmas és a képlékeny alakváltozási szakaszt általában egyetlen feszültség–alakváltozás értékpárral jellemzett ponttal szokás elválasztani, ezt hívjuk rugalmassági határnak vagy folyáshatárnak. Ennek az értéknek az ismerete mind a teherviselő gépalkatrészeket, mind a képlékeny alakváltozási technológiát tervező szakember számára fontos: az előbbinek nem szabad olyan alkatrészt tervezni, amelyben a legnagyobb terhelés hatására kialakuló feszültség eléri (vagy többnyire akár meg is közelíti) a rugalmassági határt, utóbbi számára pedig ez az a pont (ő alakítási szilárdságnak nevezi), ahol a munkadarab elkezd képlékenyen alakulni („folyni”), és amire alapozva indíthatja számításait. Az alakváltozás képlékeny szakaszára a rugalmasságtan összefüggései nem alkalmazhatók, a maradó alakváltozások rendszerint olyan nagyok, amelyek mellett a rugalmas alakváltozások elhanyagolhatók. Ezeknek a viszonyoknak a tisztázása a képlékenységtan feladata.
Történet[szerkesztés]
A képlékenységtan kialakulása Charles Augustin de Coulomb 1773-ban végzett vizsgálataival indult (csavaró kísérleteket végzett saját szerkesztésű berendezésén fémrudakon vagy fémhuzalokon), de a fémek viselkedését képlékeny alakításkor először Henri Edouard Tresca vizsgálta behatóbban 1864-ben. Megállapította, hogy a képlékeny alakváltozás egy bizonyos nagyságú csúsztatófeszültség elérésekor indul meg. A Tresca-féle elméletet Guest támasztotta alá kísérleteivel. Adhémar Jean Claude Barré de Saint-Venant felismerte, hogy a feszültségek és az alakváltozások között nincs egyértelmű összefüggés, van viszont azok növekményei között. Megfogalmazta a képlékeny síkbeli alakváltozás alapegyenleteit, amit Paul Pierre Lévy általánosított térbeli feszültségi állapotra. Az 1900-as évek elején sorra születtek a képlékenységi témájú tanulmányok: Tytus Maksymilian Huber, Richard von Mises és Heinrich Hencky lényegében egymástól függetlenül állapították meg, hogy a képlékeny alakváltozás akkor indul meg, amikor a fajlagos torzítási munka elér egy kritikus értéket (elméletüket azóta Huber–Mises–Hencky-féle folyási feltételnek nevezik). A síkbeli feszültségi állapotban lévő rugalmas-képlékeny anyagú testek anyagegyenleteit Ludwig Prandtl fogalmazta meg 1924-ben. Hencky a csúszóvonalak geometriai tulajdonságaival is foglalkozott, és komoly eredményeket ért el Sachs és Siebel is. A későbbi években szovjet kutatók értek el említésre méltó eredményeket, ők főleg a Hencky-féle alakváltozás-elméletet fejlesztették tovább (Szokolovszkij, Gubkin), az angol-amerikai kutatók inkább a Prandtl-Reuss féle elméleten dolgoztak (Hill, Prager, Hodge, Oh, Altan stb.). A kutatásokban egyre nagyobb szerepet játszott a nagy matematikai apparátus, a számítástechnika, ami az előbbi elméleteket felhasználva elvezetett napjaink végeselemes (VEM) rendszereihez.[1]
A képlékenységtani kutatásokból a magyarok is kivették részüket. Rejtő Sándor az alakítási folyamatok és a fellépő erők közötti összefüggéseket kutatta, és eredményeivel megelőzte korát. Reuss Endre 1930-ban megjelentetett tanulmányaiban a Prandtl-Reuss féle elmélet alapjait fektette le. Nádai Árpád a képlékenységtan elméletét összefoglaló könyvet írt. Orován (Orowan) Egon a képlékeny alakváltozás lényegének forradalmi, diszlokációelméleti magyarázatát fogalmazta meg. Kármán Tódor a hengerlés elméletéről írt alapvető publikációt. A képlékeny alakítás elméletének technológiai folyamatokra való alkalmazásában ért el nemzetközi szintű eredményeket Geleji Sándor, a Nehézipari Műszaki Egyetem professzora, akinek műveit sok nyelvre fordították le (még japánra is).[2] Ezt a munkát folytatta ugyanezen a tanszéken Voith Márton, aki elsősorban a képlékeny alakítás komplex hatásmechanizmusát vizsgálta.
Fémek alakváltozása[szerkesztés]



Felvetődik a kérdés: mivel magyarázható a fémek, mint kristályos anyagok alakváltozása? A fémkristályokban helyet foglaló atomok helyét rácserők határozzák meg. Ha a rácsra külső erő hat, akkor a kristályrács eltorzul: megnyúlik és megrövidül. Az egymástól távolabbra került atomok között vonzóerő, az egymáshoz közelebb kerülő atomok között pedig taszítóerő ébred. Ezek az erők tartanak egyensúlyt a külső terhelő erővel. Ha megszüntetjük a rács terhelését, akkor a kristályrács visszanyeri eredeti méreteit.[3] Az alakváltozás (ε) és a rácserő (pontosabban feszültség, σ) közötti összefüggést a Hooke-törvény írja le:
- .
Az összefüggésben szereplő E a Young–féle rugalmassági modulus, amely az adott anyagra jellemző érték.
A képlékeny alakváltozás más, bonyolultabb mechanizmus szerint megy végbe. A folyáshatár fölötti feszültség hatására a képlékeny alakváltozás elméletileg úgy mehet végbe, hogy az atomsíkok egymáson elcsúsznak. Az alakváltozás lényegét a kristályos szerkezetből kiindulva érthetjük meg. A fémekre jellemző rácsformák (felületen középpontos kockarács, térközepes kockarács, hexagonális rács) és azok csúszási síkjai különböznek egymástól. Az atomok elcsúszása azokon a kristálysíkokon valósul meg, ahol az atomok a legsűrűbben helyezkednek el.
A képlékeny alakváltozás másik lehetséges módja az ikerképződés. Ilyenkor az elmozduló részek mintegy átbillennek egy sík mentén, miközben a kristálytani irányultságuk megváltozik (ezzel szemben elcsúszáskor az irányultság változatlan marad). Az alakváltozás, azaz a kristálycsoport méretváltozása természetesen ebben az esetben is megvalósul.
A csúszáshoz, azaz az atomsíkok egymáson való elmozdításához meglehetősen nagy feszültség szükséges, mert az adott síkban lévő összes atomot egyszerre kell elmozdítani. Ez az elméletileg meghatározott feszültség azonban lényegesen nagyobb, mint a kísérletekkel kimérhető folyáshatár. A megoldást a diszlokációk adják, amelyek „segítségével” az atomsík atomjai nem egyszerre mozdulnak el egymáson, hanem egyenként, egy rácshiba révén. A reális anyagokban a képlékeny alakváltozás mindig ezek segítségével megy végbe.[4]
Diszlokációk[szerkesztés]


A fémek – normál állapotban és néhány rendkívül kivételes esettől eltekintve – kristályos szerkezetűek. Ezek a kristályok egyszerű négyzet- vagy hatszög-alapú alakzatok. Felületen középpontos kockarács jellemzi például a réz, az alumínium, a nikkel és az ezüst kristályait. A vasra és a volfrámra a térben középpontos kockarács jellemző. A magnézium, a cink és a titán hexagonális rendszerben kristályosodik.[5] Itt csak megjegyezzük, hogy a jelzett fémek kristályformái szobahőmérsékleten érvényesek, más hőmérsékleteken egyéb allotrop módosulatok is kialakulhatnak. Mint korábban már szó volt róla, a képlékeny alakváltozás az atomsíkok elcsúszásával valósul meg. Az elcsúszás azokon a síkokon megy végbe, ahol a legtöbb atom található. Például a lapközepes kockarács {110} síkjában négy, az {100} síkban öt, az {111} síkban pedig hat atom található. Ennek megfelelően ez utóbbi a csúszási sík (az ábrán a piros vonalakkal jelölt síkok).[6] Az atomsíkok elcsúszása azonban nagy csúsztatófeszültséget igényel, a csúszás megindításához és fenntartásához elméletileg mintegy ezerszer akkora feszültségre lenne szükség, mint amit kísérletekkel mértek. Ezt az ellentmondást a diszlokációelmélet oldotta fel, amelyet – egy időben, de végső soron egymástól függetlenül – Orován Egon, Polányi Mihály és G. I. Taylor terjesztett ki a fémek képlékeny alakváltozására az 1930-as években. Eszerint a kristálysíkok elcsúszása nem az atomsíkok merev testhez hasonlítható elcsúszásával megy végbe, hanem kristályhibák közvetítésével, az atomsor a diszlokációk segítségével mintegy „végiggörög, végigfut” a másik atomsoron.
A gyakorlati fémekben jelentős mennyiségű kristályosodási hiba, diszlokáció és ponthiba található. A képlékeny alakváltozás szempontjából a diszlokációk hatása a meghatározó, maguk a ponthibák inkább a diszlokációkra hatnak.
Kétféle diszlokáció van:
- éldiszlokáció és
- csavardiszlokáció.
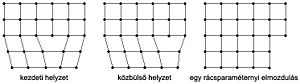
A magyarázat szempontjából egyszerűbb az éldiszlokációkkal foglalkozni. Éldiszlokáció alakulhat ki kristályhatárokon, ahol a két szemcse dőlt határ mentén érintkezik egymással. Az ezt ábrázoló ábrán (az oldal tetején) a határ kristályszerkezete és az érintkezési felületen az egymástól d távolságban elhelyezkedő éldiszlokációk láthatók (fordított T-alakkal jelölve). A fémek dermedésekor sok, különböző irányítottságú kristálycsíra alakul ki, amelyből olyan sokkristályos szerkezet jön létre, amelyben sok a diszlokáció. Az öntött fémekben a diszlokációsűrűség (amelyet általában felületegységre vonatkoztatnak) 1010…1012 m−2. A diszlokációk környékén a rácstorzulás miatt jelentős nagyságú feszültségi energia halmozódik fel. A képlékeny alakváltozás az atomokat összetartó belső erők legyőzésével valósítható meg. Amennyiben a csúszás (transzláció) síkjában diszlokáció található, akkor ez az aktivizálódott térrész eléri azt az energiaszintet, amely az elcsúszáshoz szükséges. A képlékeny alakváltozás folyamán a diszlokációk megsokszorozódnak (akár 1015 m−2 nagyságrendig), emiatt gátolják egymás mozgását. A felhalmozódott feszültségi energia az alakított fémben alakítási keményedést okoz, megváltoznak a fém mechanikai tulajdonságai és szemcseszerkezete.[7] A jelenség azonban különböző módon hat hideg- és melegalakításkor. (Tudni kell, hogy a hideg- és a melegalakítást az újrakristályosodási hőmérséklet választja el egymástól.)


Hidegalakításkor a képlékeny alakváltozás során megváltozott tulajdonságok megmaradnak, azok csak újrakristályosító izzítással szüntethetők meg. Ennek során az alakítás során eltorzult (megnyúlt) szemcsékből arányos méretű, új orientáltságú szerkezetek keletkeznek, miközben a diszlokációsűrűség az eredeti értékre áll vissza. Melegalakításkor – minthogy eleve az újrakristályosodási hőmérséklet felett történik az alakítás – az újrakristályosodás és ezzel az eredeti tulajdonságok visszaállása az egymást követő alakítási fázisok (hengerlési szúrások, kovácsoló ütések stb.) között általában végbemegy (csak a nagysebességű alakítások jelenthetnek kivételt).
A hidegen alakított fémben a diszlokációk felhalmozódva rögzítik egymást, amelyek külső energia nélkül nem tudnak oldódni. A diszlokációk a mechanikai terhelésen kívül hőenergiával is aktiválhatók. A hőenergia lehetővé teszi, hogy a diszlokációk elhagyják a csúszási síkjukat, és így lehetővé válik az újrakristályosodás.[8]
Képlékeny anyagok[szerkesztés]
Anyagmodellek[szerkesztés]

A képlékeny alakváltozások leírására alkalmas függvények megalkotása érdekében anyagmodelleket hoztak létre. Az anyagmodellek szükségszerűen kisebb-nagyobb egyszerűsítéseket, célszerűen megválasztott elhanyagolásokat tartalmaznak, és annak megfelelően választják ki jellemzőiket, ideális alaptulajdonságaikat, hogy milyen célú közelítésre szánják. Az anyagmodellek között megtaláljuk a merev testek, a rugalmas-izotróp testek, valamint a tökéletes és a szívós folyadékok fogalmát. A végeselemes rendszerek például merev testekkel operálnak, a képlékeny alakváltozás egyéb leírására más esetekben gyakran használják a folyadék anyagmodelleket.
A legegyszerűbb anyagmodelleket úgy kapjuk, hogy a valóságos szakítódiagram jellemző szakaszait egyenesekkel helyettesítik. Ennek megfelelően a rugalmasságtanban és a képlékenységtanban a következő lineáris anyagmodelleket használják:
- a) lineárisan rugalmas anyag,
- b) merev – tökéletesen képlékeny anyag,
- c) merev – lineárisan képlékeny anyag,
- d) lineárisan rugalmas – tökéletesen (lineárisan) képlékeny anyag,
- e) lineárisan rugalmas – lineárisan keményedő anyag.
A felsorolt anyagmodellek közül képlékenységtani vizsgálatokra – az első kivételével – valamennyit használhatják. Azokban az esetekben, amikor a rugalmas alakváltozások elhanyagolhatók a képlékenyhez képest, a b) és c) jelű modellek használhatók, amelyeknél a rugalmas szakaszt függőleges vonal jelzi. Ezeknél a mechanikai terhelés hatására eleinte semmilyen alakváltozás nem történik, ha azonban a fém eléri a folyási határt, akkor megindul a képlékeny alakváltozás. Ha a rugalmas hatás számottevő mértékű, illetve nem hanyagolható el, akkor a d) és e) anyagmodellek jöhetnek szóba. A fémek a hidegalakítás során keményednek. Ezt a hatást a c) és e) jelű anyagmodell veszi figyelembe, a képlékeny szakaszt jelképező egyenesek „ferde” futásával.[9]
Képlékenység[szerkesztés]


A képlékenység az anyagok olyan tulajdonsága, amely lehetővé teszi, hogy alakjuk külső terhelés hatására maradandóan megváltozzon anélkül, hogy az atomok közötti kötés megszakadna, azaz alakváltozás közben az anyagban szakadás, törés következne be. A fémek képlékenysége kristályos tulajdonságaikkal magyarázhatók. A képlékeny alakítás gyártástechnológiája összefügg a darabok mechanikai terhelhetőségével és a gazdaságossággal. A mechanikai terhelhetőség az anyagminőséggel, a szövetszerkezettel és a diszlokáció-szerkezettel van összefüggésben. A szövetszerkezetet a benne lévő fázisok és ezek eloszlása határozza meg.
A folyási feszültség a fém diszlokációsűrűségétől, az pedig a szemcsemérettől függ: annál nagyobb a folyási feszültség, minél kisebb a szemcseméret. Hidegalakítás után a szemcseméret csökkentését újrakristályosítással meg lehet valósítani, de a helyesen megválasztott melegalakítási technológiával is lehet biztosítani a kis méretű szemcséket. Túl nagy alakítási hőmérséklet esetén durva szemcsék keletkeznek, túl kicsi hőmérséklet esetén pedig az újrakristályosodás nem megy végbe megfelelően. Minden melegalakítási technológiának van tehát egy optimális befejező hőmérséklete, amely kedvező szemcseméretet biztosít. Más oldalról nézve: létezik olyan kritikus szemcseméret, amely fölött a képlékeny anyag rideggé válik. Ennek oka az, hogy a túl nagy szemcseméret esetén a szemcsék közötti anyaghidak olyan szélesekké válnak, hogy alakváltozás közben mintegy kiszakadnak az anyagból, ezzel pedig törést okoznak. A szemcseméret csökkentésével tehát nem csak a fém szilárdsága, hanem képlékenysége is javul.[10]
A képlékenység nem azonos a fém alakíthatóságával. Az alakíthatóság vagy alakváltozó képesség az alakváltozásnak azt a mértékét jelenti, amelyet a fém a törésig (repedésig) el tud viselni. Az alakíthatóságra többféle mérőszám is használatos:[11]

- vagy ,
ahol Am a szakadási nyúlás, φm a szakadásig végbement alakváltozás, ηal pedig az alakváltozási hatásfok.
Más definíció szerint az adott fém annál jobban alakítható, minél kisebb a φ alakváltozáshoz felhasznált w fajlagos munka:
- .
Az alakíthatóságot befolyásoló tényezők a feszültségállapot, az alakváltozási sebesség és a hőmérséklet. A feszültségi állapot minél inkább a nyomófeszültség tartományában van, annál jobb az alakíthatóság (ezért lehet például kisajtolással sokkal nagyobb alakváltozást elérni, mint húzással). Ezt a hatást a feszültségi középérték (hidrosztatikus tag, σ0) és az alakítási szilárdság hányadosának függvényében szokás ábrázolni. Az alakváltozási sebesség hatása eltérő az egyes fémeknél. Alumínium hidegalakításakor gyakorlatilag az alakíthatóság javul, erősen ötvözött acélok, titánötvözetek esetén romlik. Acélok melegalakításakor növekvő alakítási sebességnél javul az alakíthatóság. A hőmérséklet hatása egyértelmű: emelésével jobb lesz az alakíthatóság.[12]
Szuperképlékenység[szerkesztés]
A szuperképlékenység a fémek olyan tulajdonsága, amikor azok meghatározott állapotban – mechanikai sérülés, azaz szakadás, törés nélkül – igen nagy alakváltozásra képesek. A jelenség ismert, mechanizmusa sok tekintetben még nem eléggé feltárt. Különösen igaz ez az acélok szuperképlékeny alakváltozására. A szuperképlékenységnek három változata ismert:[13]
- Finomszemcsés szerkezeti szuperképlékenység: a szuperképlékeny viselkedést az alakítási hőmérséklet (> 0,5·(Tolv+273), °C), az alakváltozási sebesség (< 10−2 s−1) és a finomszecsés szerkezet (< 10 μm) határozza meg.
- Szubkritikus szuperképlékenység: a fázisátalakulási hőmérséklet alatt megfigyelhető nagyobb képlékenység.
- Martenzites szuperképlékenység: a martenzites átalakulás során észlelhető képlékenység növekedés.
Feszültségállapot és alakváltozás-állapot[szerkesztés]

A fémek képlékeny alakváltozásához külső erőkre van szükség. Ezek hatására a testben olyan belső megoszló erőrendszer (feszültség) ébred, amely biztosítja a test bármely kiragadott részének az egyensúlyát. A terhelt test síkmetszetének minden pontjához egy p vektorral jellemzett feszültség kapcsolható, amely felbontható a síkra merőleges σ normálfeszültségre és a síkba eső τ csúsztatófeszültségre. Az adott pont feszültségi állapotát akkor tekinthetjük meghatározottnak, ha ismerjük a ponton átfektetett, három egymásra merőleges metszetre ható feszültségvektort (px, py, pz), illetve ezek összetevőit, azaz ismert a feszültségtenzor, amely a három vektor kilenc elemét foglalja össze:[14]
- .
A σij feszültségtenzor összetevőit elemi kockán lehet ábrázolni.
A vizsgált test valamennyi pontjában található három egymásra merőleges metszet, amelyekben a csúsztatófeszültség értéke zérus. Ezekben a síkokban csak a normálfeszültségek működnek, amelyeket főfeszültségnek neveznek, és római számokkal indexelik. A megegyezés szerint a legnagyobb kapja az I, a legkisebb a III indexet:[15]
- .
A képlékenységtani feladatok megfogalmazása sokkal egyszerűbbé válik, ha ismerjük a főfeszültségeket és főirányokat. A feszültségtenzor alakja a főirányokkal egybeeső koordináta-rendszerben:
- .
Azokban a síkokban, amelyek az egyik főtengellyel párhuzamosak és a másik kettővel 45°-os szöget zárnak be, a nyírófeszültség:
- ,
illetve a másik kettő (τII és τIII) is hasonló alakban írható fel.[16]


A feszültségek szempontjából kitüntetettnek számítanak azok a síkok, amelyek mindhárom főtengellyel azonos szöget zárnak be, tehát normálvektoruk iránykoszinusza . Ezek a síkok egymással oktaédert alkotnak, ahol a normálfeszültség és a nyírófeszültség egyforma. Az oktaéderes nyírófeszültség:[17]
- .
A feszültségállapot legszemléletesebben az ún. Mohr-körök segítségével magyarázhatók. A nyugalomban lévő test elemi kockájára ható feszültségek egyensúlyban vannak, ami azt jelenti, hogy összegük zérus.[18]
A képlékeny alakváltozás mértékét többféle mérőszámmal is jellemezhetjük.[19] A legegyszerűbb az, amikor az alakváltozás előtti és az alakváltozott méretek különbségét vesszük (a következő képletekben a magasságot h-val, a szélességet b-vel, a hosszúságot l, a keresztmetszet területét A betűvel jelöljük, az indexekben 0 jelöli a kiinduló, 1 a művelet utáni állapotot):
- .
Az abszolút alakváltozási mérőszámokból adódnak a relatív mérőszámok, amelyek esetén az abszolút méretkülönbségeket a kiinduló mérethez viszonyítjuk és ε-nal jelöljük:
- .

A térfogatállandóság törvénye értelmében egy prizmatikus test alakváltozása kapcsán írható:
- ,
ami azt fejezi ki, hogy az alakváltozás során a darab térfogata változatlan marad, csak a méretei változnak. Átalakítás után:
- .
Az összefüggés tényezői sorban a különböző irányú alakváltozásokra jellemző értékeket adják:
- – a nyújtási tényező, – a szélesedési tényező, – a duzzasztási tényező.
A fenti összefüggés természetes logaritmusát véve a φ-vel jelölt logaritmikus alakváltozások értékeit kapjuk:
- , azaz:
- .
Az alakváltozás-tenzor a feszültségtenzor mintájára írható:
- .
Az alakváltozási feladatok fontos mérőszáma az alakváltozási sebesség is. Értelmezése: az alakváltozás növekményét elosztjuk a létrejöttükhöz szükséges időnövekménnyel:
- , illetve: .
Az alábbi táblázat néhány jellegzetes művelet hozzávetőleges alakváltozási sebességeit tartalmazza:[20][21]
| Művelet | Alakváltozási sebesség s−1 |
|---|---|
| Szakító vizsgálat | 0,25 |
| Csavaró vizsgálat | max. 30 |
| Kovácsolás kalapácson | 50…500 |
| Előnyújtó hengerlés | 10 |
| Szélesszalag meleghengerlés | 100…200 |
| Szélesszalag hideghengerlés | 100…1000 |
| Huzalhengerlés | max. 104 |
Képlékenységi feltételek[szerkesztés]
A képlékeny alakváltozás akkor jön létre, ha a darab keresztmetszetében ható mechanikai feszültség elér egy, az anyagminőségre és az állapotjelzőkre (feszültségállapot, alakváltozási sebesség és hőmérséklet) jellemző feszültséget, a folyáshatárt (σf), azaz az alakítási szilárdságot (kf).[22]
Egytengelyű igénybevétel esetén a képlékeny szakaszra – az anyagmodellek b) esete szerinti merev – tökéletesen képlékeny anyagot tekintve – a folyási feltétel
- , azaz
alakban írható fel. A gyakorlatban azonban igen ritkán fordul elő az egytengelyű feszültségállapot (a szakítókísérlet is csak közelíti), a tényleges igénybevétel általában térbeli. Térbeli igénybevételek esetén a σij feszültségtenzornak hat komponense van, amelyek adott kombinációja esetén képlékeny alakváltozás valósul meg. A képlékenységi (folyási) feltételnek olyannak kell lenni, amely megadja a feszültségek valamennyi olyan kombinációját, amelynek bekövetkezése a képlékeny állapot kezdetét jelenti. Fontos megjegyezni, hogy a feszültségtenzor hat eleme háromra csökkenhet, ha a feszültségi főirányokat koordinátatengelynek választjuk:
- ,
illetve ha az f függvény független a koordinátatengelyek irányától, a feszültségtenzor elemei helyett a tenzor invariánsai írhatók. Mivel a feszültségtenzor hidrosztatikus része maradó alakváltozást nem okoz, ezért a feszültségdeviátor tenzortól függ a képlékeny alakváltozás:
- .
A feszültségdeviátor tenzor első invariánsa mindig zérus, így a folyási feltétel általános alakja:
- .[23]
A Huber–Mises–Hencky-féle folyási feltétel[szerkesztés]

Huber, Mises és Hencky a 20. század elején fogalmazta meg folyási feltételüket:[24]
- .
Az összefüggésben K2 a feszültségdeviátor-tenzor invariánsa, τf az a csúsztatófeszültség, ami képlékeny folyást hoz létre. A H–M–H-féle folyási feltétel kifejtve:
- .
Ezt a függvényt a derékszögű koordináta-rendszerben egy ferde henger ábrázolja, ahol a képlékeny alakváltozás a henger palástján jön létre. Ezért a folyást megindító feszültség (alakítási szilárdság, kf) meghatározásához a henger sugarát kell kiszámítani:
- .
Síkbeli feszültségi állapotot vizsgálva az egyik főfeszültség zérus. Ha például σIII = 0, akkor a σI – σII síkban a henger metszésvonalaként adódó ellipszist kapjuk. A kf értékének meghatározásához az ellipszis főtengelyének hosszát kell ismerni. Ezzel a H–M–H-féle folyási feltétel elterjedt alakja:
- .
A Tresca–Guest–Mohr-féle folyási feltétel[szerkesztés]

Henri Tresca francia mérnök abból indult ki, hogy a képlékeny alakváltozás létrejötte csak a nyírófeszültségtől függ, és maradó alakváltozás akkor lép fel, ha a legnagyobb nyírófeszültség eléri azt az értéket, amely tiszta nyírás esetén folyást idézne elő. Ez a legnagyobb nyírófeszültség elve.[25] A folyási feltétel ennek megfelelően:
- .
Levezetéseket és más magyarázatokat mellőzve a T–G–M-féle folyási feltétel a derékszögű koordináta-rendszerben egy hatszögű hasábnak felel meg, ahonnan:
- .
Síkbeli állapotot tekintve:
- .
Jegyzetek[szerkesztés]
- ↑ Szabó László 1992 2–12. oldal
- ↑ Voith Márton 1998 5–6. oldal
- ↑ Gácsi–Mertinger 2000 21. oldal
- ↑ Voith Márton 1998 9–12. oldal
- ↑ Voith Márton 1998 35. oldal
- ↑ Gácsi–Mertinger 2000 22–23. oldal
- ↑ Voith Márton 1998 35–38. oldal
- ↑ Voith Márton 1998 38–41. oldal
- ↑ Voith Márton 1998 52–58. oldal
- ↑ Voith Márton 1998 63–66. oldal
- ↑ Kiss Ervin 1987 40. oldal
- ↑ Voith Márton 1998 77–80. oldal
- ↑ Voith Márton 1998 71–75. oldal
- ↑ Voith Márton 1998 91. oldal
- ↑ Voith Márton 1998 93. oldal
- ↑ Voith Márton 1998 95–96. oldal
- ↑ Voith Márton 1998 96. oldal
- ↑ Kiss Ervin 1987 28–29. oldal
- ↑ Kiss Ervin 1987 30–35. oldal
- ↑ Voith Márton 1998 23. oldal
- ↑ Kiss Ervin 1987 35. oldal
- ↑ Kiss Ervin 1987 42. oldal
- ↑ Voith Márton 1998 113–115. oldal
- ↑ Voith Márton 1998 115–118. oldal
- ↑ Voith Márton 1998 118–121. oldal
Források[szerkesztés]
- ↑ Voith Márton 1998: Voith Márton. A képlékenyalakítás elmélete – Nagy alakváltozások tana. Miskolc: Egyetemi Kiadó, 300. o. (1998). ISBN 963-661-315-x
- ↑ Geleji Sándor 1967: Geleji Sándor. A fémek képlékeny alakításának elmélete. Budapest: Akadémiai Kiadó, 422. o. (1967)
- ↑ Kiss Ervin 1987: szerk.: Kiss Ervin: Képlékeny alakítás. Budapest: Tankönyvkiadó, 702. o. (1987). ISBN 963-17-9492-X
- ↑ Gácsi–Mertinger 2000: Gácsi Zoltán, Mertinger Valéria. Fémtan. Budapest: Műszaki Könyvkiadó (2000)
- ↑ Szabó László 1992: Szabó László. A süllyesztéküregben végbemenő alakváltozások elemzése – Doktori értekezés (1992)





























![{\displaystyle f={\frac {1}{6}}\cdot \left[(\sigma _{I}-\sigma _{II})^{2}+(\sigma _{II}-\sigma _{III})^{2}+(\sigma _{III}-\sigma _{I})^{2}\right]-\tau _{f}^{2}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/113fb622cb9e44fb1ac413e425a76f6424eebfb2)

![{\displaystyle k_{f}={\frac {1}{\sqrt {2}}}\cdot \left[(\sigma _{I}-\sigma _{II})^{2}+(\sigma _{II}-\sigma _{III})^{2}+(\sigma _{III}-\sigma _{I})^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3e63b2b3b90dd070199bf36b0ed20f072fe10fa)


