Grafikon (matematika)
|
|
Ez a szócikk vagy szakasz lektorálásra, tartalmi javításokra szorul. |
A grafikon a diagram egyik fajtája, amely két változó kapcsolatát egy derékszögű koordináta-rendszerben ábrázolja. A két tengely jelképezi a két változót, és a grafikon görbéje jelzi, hogy az egyik változó egyes értékeihez a másik mely értékei tartoznak. Általában két mennyiség korrelációjának, vagy egy mennyiség időbeli változásának bemutatására használják. Matematikai szemszögből a grafikon egy függvényt ábrázol.
A rokon matematikai definíció szerint az f(x) függvény grafikonja vagy gráfja az (x,f(x)) alakú párokból álló halmaz. Ha ezeket a párokat egy koordináta-rendszerben helyezzük el, és ezzel a függvényt görbével vagy felülettel ábrázoljuk, akkor mondjuk, hogy felrajzoljuk a szóban forgó függvény grafikonját, vagy ábrázoltuk az adott függvényt. Hasonlóan lehet a reláció grafikonját vagy gráfját is értelmezni.
Példák[szerkesztés]
Ennek a függvénynek a grafikonja az {(1,a), (2,d), (3,c)} párokból álló halmaz.
A grafikonok nagyban függnek attól, hol értelmeztük az adott függvényt.
- az izolált pontokban értelmezett függvény grafikonja izolált pontokból fog állni
- ha egy intervallumra szűkítünk le egy valós-valós függvényt, akkor a grafikon a teljes görbe egy darabja lesz
-
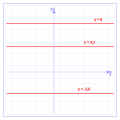
A konstans függvények grafikonja egy vízszintes egyenes.
-
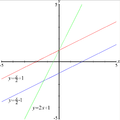
A lineáris függvény grafikonja egy egyenes – az ábrán a piros és a kék meredeksége (m) ugyanaz, míg a pirosnak és a zöldnek az y-tengelymetszete (b) egyezik meg.
-
A másodfokú függvények grafikonja parabola.
-
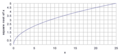
A négyzetgyökfüggvény grafikonja egy fél parabola.
-
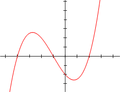
Egy harmadfokú függvény grafikonja.
-
Az abszolútérték-függvény grafikonja.
-
A szignumfüggvény grafikonja két félegyenesből és egy pontból áll.
-
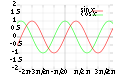
A tangens függvény grafikonja.
-
Az egészrészfüggvény grafikonja.
-
A törtrészfüggvény grafikonja.
-
Hiperbolikus függvények (csch, sch és cth) grafikonja.
-
Egy exponenciális függvény grafikonja.
-
Logaritmusfüggvények grafikonja.
-
Törtlineáris függvény grafikonja.
Tágabb értelemben a magasabb fokú polinomfüggvények grafikonját is parabolának nevezzük.
A reciprokfüggvény grafikonja hiperbola.
Függvény inverzének a grafikonja az eredeti függvény grafikonjának tükörképe az x=y tengelyre.
Források[szerkesztés]
- Harsányi Zsuzsa: Matematika I. Halmazok, függvények, algebra I.
- Kosztolányi József - Kovács István - Pintér Klára - Urbán János - Vincze István: Sokszínű matematika
- dr. Pintér Lajos: Analízis I.
- Obádovics J. Gyula: Matematika