Rayleigh-eloszlás

A valószínűség-számítás elméletében, és a statisztika területén a Rayleigh-eloszlás egy folytonos valószínűség eloszlás.

A Rayleigh-eloszlás gyakran megfigyelhető, amikor egy vektor nagyságrendje kapcsolatban van az irány komponenseivel.

Egy tipikus példa a Rayleigh-eloszlásra, mely a természetben is megfigyelhető, amikor a szél sebességét analízálják az ortogonális két dimenziós vektor komponensei szerint. Feltételezve, hogy a komponeneseknek nincs korrelációjuk egymással, és normális eloszlásúak, hasonló szórásnégyzettel, akkor a szél sebességét a Rayleigh eloszlás jellemzi.

Egy következő példa az algebrából: véletlenszerű komplex számok esetében, ahol a valós és imaginárius komponensek függetlenek és azonos eloszlásúak. Ebben az esetben a komplex szám abszolút értéke Rayleigh-eloszlású.

Az eloszlást, felfedezőjéről, John William Strutt, Rayleigh III. lordjáról nevezik Rayleigh-eloszlásnak.

A Rayleigh-féle valószínűségsűrűség-függvény:

$f(x;\sigma) = \frac{x}{\sigma^2} e^{-x^2/2\sigma^2}, \quad x \geq 0,$

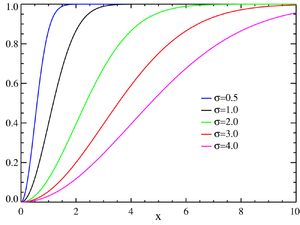
ahol $\sigma >0,$ és a kumulatív eloszlás függvény:

$F(x) = 1 - e^{-x^2/2\sigma^2}$

ahol $x \in [0,\infty).$

Tulajdonságok

A Rayleigh-eloszlás sűrűségfüggvénye

Rayleigh-féle kumulatív eloszlásfüggvény

A nyers momentum:

$\mu_k=\sigma^k2^{k/2}\,\Gamma(1+k/2)\,$

ahol $\Gamma(z)$ a gamma függvény. A Rayleigh-féle valószínűségi változó középértéke és szórásnégyzete:

$\mu(X) = \sigma \sqrt{\frac{\pi}{2}}\ \approx 1.253 \sigma,$

és

$\textrm{var}(X) = \frac{4 - \pi}{2} \sigma^2\ \approx 0.429 \sigma^2.$

$f_\text{max} = f(\sigma;\sigma) = \frac{1}{\sigma} e^{-\frac{1}{2}} \approx \frac{0.606}{\sigma}$

A ferdeség:

$\gamma_1=\frac{2\sqrt{\pi}(\pi - 3)}{(4-\pi)^{3/2}} \approx 0.631.$

A többlet lapultság:

$\gamma_2=-\frac{6\pi^2 - 24\pi +16}{(4-\pi)^2} \approx 0.245.$

A karakterisztikus függvény:

$\varphi(t)=1\!-\!\sigma te^{-\sigma^2t^2/2}\sqrt{\frac{\pi}{2}}\!\left(\textrm{erfi}\!\left(\frac{\sigma t}{\sqrt{2}}\right)\!-\!i\right)$

ahol $\operatorname{erfi}(z)$ a képzetes hiba függvény.

A momentum-generáló függvény:

$M(t)=1+\sigma t\,e^{\sigma^2t^2/2}\sqrt{\frac{\pi}{2}} \left(\textrm{erf}\left(\frac{\sigma t}{\sqrt{2}}\right)\!+\!1\right),$

ahol $\operatorname{erfi}(z)$ a hiba függvény,

Információ entrópia

Az információ entrópia, vagyis a Shannon-entrópiafüggvény: $H=1+\ln\left(\frac{\sigma}{\sqrt{2}}\right)+\frac{\gamma}{2}$

ahol $\gamma$ az Euler–Mascheroni állandó.

Paraméter becslés

N darab független és azonos eloszlású Rayleigh valószínűségi változó esetén, a $\sigma$ maximális valószínűsége:

$\hat{\sigma}\approx \!\,\sqrt{\frac{1}{2N}\sum_{i=1}^N x_i^2}.$

A $\sigma$ értékének becslése az MRI képalkotó technikában is használatos, ahol az MRI képelemek komplex alkotókból állnak, és a háttér adat Rayleigh eloszlású. A fenti összefüggés segítségével megbecsülhető a hiba szórás a MRI hattér adatokból.

Rayleigh-eloszlású valószínűségi változók generálása

Ha adva van egy állandó eloszlás-ból származó U valószínűségi változó, (0, 1) tartományban, akkor a valószínűségi változó:

$X=\sigma\sqrt{-2 \ln(1-U)}\,$

Rayleigh-eloszlású lesz $\sigma$.paraméterel. Ez a kumulatív eloszlás függvényből következik. Ha U egységes (uniformizált), (1–U)-nek is hasonló tulajonsága lesz, a fenti összefüggés egyszerűsíthető:

$X=\sigma\sqrt{-2 \ln(U)}.$

Megjegyzés: ha véletlen számokat generálunk [0,1) tartományban, a zérót kizárjuk, hogy elkerüljük a zeró természetes logaritmusát.

Kapcsolódó eloszlások

• Ha $R \sim \mathrm{Rayleigh}(\sigma)$ Rayleigh-eloszlású, akkor $R = \sqrt{X^2 + Y^2}$, ahol $X \sim N(0, \sigma^2)$, és $Y \sim N(0, \sigma^2)$ független normál valószínűségi változók.(Ez teszi lehetővé a $\sigma$ szimbólum alkalmazását a fenti Rayleigh-sűrűségfüggvény parametrizálásánál.
• Ha $R \sim \mathrm{Rayleigh} (1)$, akkor $R^2$ khínégyzet-eloszlású. két szabadságfokkal: $R^2 \sim \chi^2_2$
• Ha X exponenciális eloszlású , akkor $X \sim \mathrm{Exponential}(\lambda)$, then $Y=\sqrt{2X\sigma^2\lambda} \sim \mathrm{Rayleigh}(\sigma)$.
• Ha $R \sim \mathrm{Rayleigh}(\sigma)$, akkor $\sum_{i=1}^N R_i^2$ gamma-eloszlású, $N$ and $2\sigma^2$: $[Y=\sum_{i=1}^N R_i^2] \sim \Gamma(N,2\sigma^2)$ paraméterekkel.
• A Khí-eloszlás a Rayleigh-eloszlás egy általánosítása
• A Rice-eloszlás a Rayleigh-eloszlás egy általánosítása
• A Weibull-eloszlás a Rayleigh-eloszlás egy általánosítása. Ez esetben a sigma paraméter kapcsolódik a Weibull-skálaparaméterhez $\lambda$:

$\lambda = \sigma \sqrt{2}$.

• A Maxwell–Boltzmann-eloszlás írja le a normál vektor nagyságrendjét három dimenzióban.

Kapcsolódó szócikkek

• Valószínűség-számítás
• Statisztika
• Rayleigh-fading
• Maxwell–Boltzmann statisztika
• Boltzmann-eloszlás
• Maxwell sebesség eloszlás
• Matematikai statisztika
• Khí-négyzet eloszlás
• Normális eloszlás
• Szórás
• Gamma-eloszlás
• Nakagami-eloszlás
• Norma
• Valószínűségi változó
• Weibull-eloszlás
• Rice-eloszlás
• MRI
• Szórásnégyzet
• Shannon-entrópiafüggvény
• Entrópia
• Karakterisztikus függvény:
• Lapultság