Matematikai közepek

A matematikában négy nevezetes középértéket különböztetünk meg: a harmonikus közép, a mértani közép, a számtani közép és a négyzetes közép. Az ezek közötti összefüggés: $H(a_{1};...;a_{n})\leq M(a_{1};...;a_{n})\leq A(a_{1};...;a_{n})\leq N(a_{1};...;a_{n})$ Természetesen létezik k-adik hatványközép, azaz bárhányadik hatványú közép. A számtani, harmonikus, és négyzetes közép is felfogható hatványközépként, rendre első, mínusz egyedik, és második.

A harmonikus közép

Harmonikus középértéken a számok reciprokaiból számított számtani közép reciprokát értjük. A harmonikus közepet általában $\,H$ betűvel jelöljük.

$H(a_{1};...;a_{n})={\frac {1}{\frac {{\frac {1}{a_{1}}}+...+{\frac {1}{a_{n}}}}{n}}}={\frac {n}{{\frac {1}{a_{1}}}+...+{\frac {1}{a_{n}}}}}$

A mértani közép

Mértani vagy geometriai középértéken $\,n$ szám szorzatának n-ed fokú gyökét értjük. Általában $\,G$-vel vagy $\,M$-mel jelöljük.

$G(a_{1};...;a_{n})={\sqrt[{n}]{a_{1}\cdot a_{2}\cdot a_{3}\cdot ...\cdot a_{n}}}$

A számtani közép

Számtani vagy aritmetikai középértéken $\,n$ darab szám átlagát, azaz a számok összegének $\,n$-ed részét értjük. A számtani közepet általában $\,A$ betűvel jelöljük:

$A(a_{1};...;a_{n})={\frac {a_{1}+...+a_{n}}{n}}$

A négyzetes közép

Négyzetes középértéken $\,n$ darab szám négyzetéből számított számtani közép négyzetgyökét értjük. A jele általában: $\,N$.

$N(a_{1};...;a_{n})={\sqrt {{1 \over n}\sum _{i=1}^{n}a_{i}^{2}}}={\sqrt {{a_{1}^{2}+a_{2}^{2}+\cdots +a_{n}^{2}} \over n}}$

A közepek közötti összefüggések

$H(a_{1};...;a_{n})\leq G(a_{1};...;a_{n})\leq A(a_{1};...;a_{n})\leq N(a_{1};...;a_{n})$

ahol

$\qquad a_{i}\in \mathbb {R} _{0}^{+},\quad n\in \mathbb {Z^{+}}$

A közepek közötti összefüggések vizuálisan (trapéz)

A közepek „mértékei” megmutathatóak egy trapézban, ha a trapéz alapjainak középértékeit szeretnénk megmutatni.

Számtani közép

A trapéz szárainak felezőpontjait összekötő szakasz az alapok számtani közepe hosszúságú.
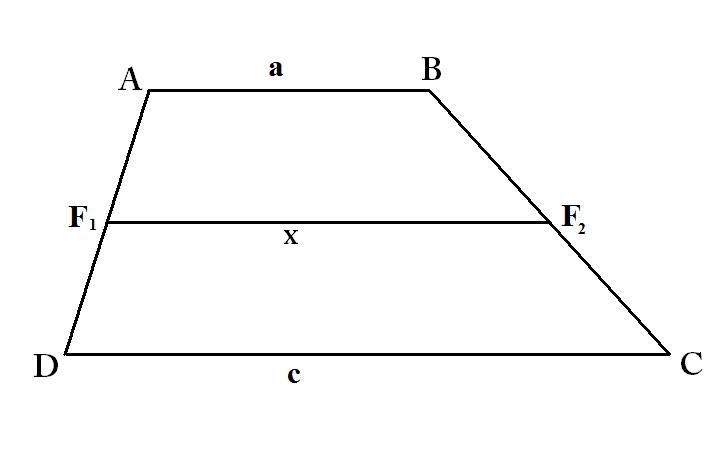
Az ábrán: $x={a+c \over 2}$

Bizonyítás

Az ábrán $p+q=c-a$ a trapéz tulajdonságai miatt. $F_{1}I$ szakasz középvonal $ADK$ háromszögben, ezért hossza: $p \over 2$, ugyanezért $JF_{2}={q \over 2}$. Tehát $F_{1}F_{2}$ hossza: $x=a+{p \over 2}+{q \over 2}=a+{{c-a} \over 2}={a+c \over 2}$

Harmonikus közép

A trapéz átlóinak metszéspontján átmenő, az alapokkal párhuzamos szakasz hossza az alapok harmonikus közepe hosszúságú.
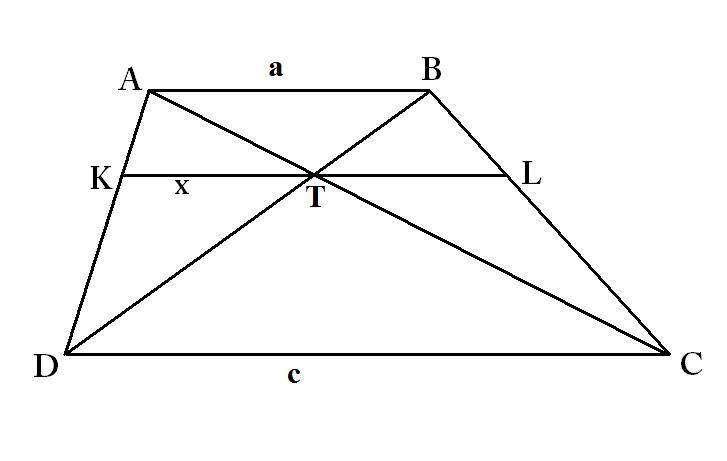
Az ábrán: $KL={\frac {1}{\frac {{\frac {1}{a}}+{\frac {1}{c}}}{2}}}={2ac \over a+c}$

Bizonyítás

Az ábrán $ABT$ hasonló $CDT$-hez, mert megfelelő szögeik egyenlő nagyságúak (A T-nél lévő szög csúcsszög, a másik kettő pedig a párhuzamosság miatt). A megfelelő oldalak aránya tehát: ${a \over c}={p \over q}$, akkor ${a+c \over c}={p+q \over q}$. Az $ABD$ háromszögben alkalmazva a párhuzamos szelőszakaszok tételét: ${x \over a}={q \over p+q}={c \over a+c}$. Innen: $x={ac \over a+c}$. Ezt $ABC$-vel is elvégezve adódik: $KL=x+y={2ac \over a+c}$.

Négyzetes közép

Ha a trapézt két ugyanakkora területű trapézra vágjuk, akkor annak a szakasznak a hossza, mellyel elvágtuk, a trapézon belül a két alap négyzetes közepe hosszúságú.
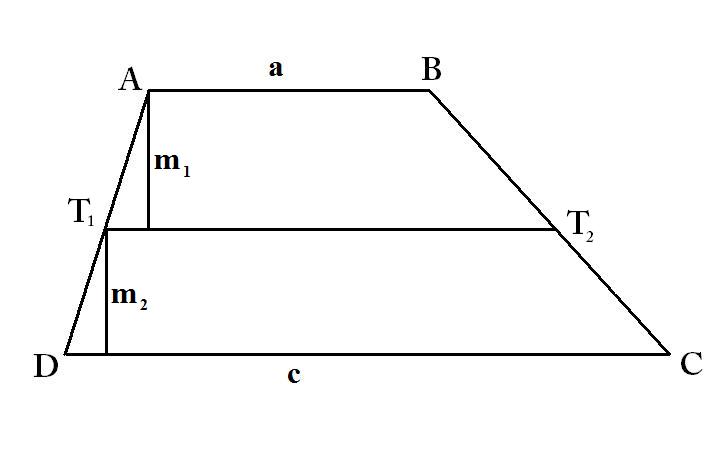
Az ábrán: $x={\sqrt {{a^{2}+c^{2}} \over 2}}$

Bizonyítás

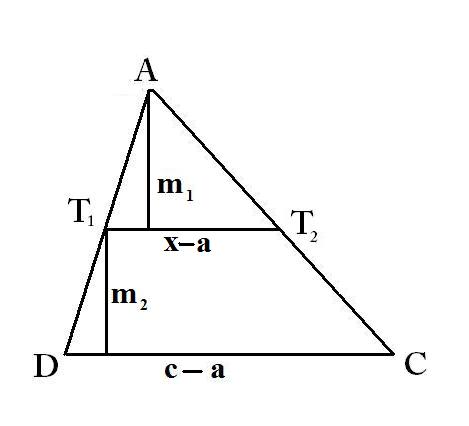
Az ábra úgy keletkezett, hogy a trapézt zsugorítottuk, pontosabban kivágtunk belőle egy $a$ hosszúságú részt. Az ábrán lévő háromszögben felírom az oldalak arányát, melynek négyzete egyenlő a területek arányával, hisz a területek négyzetesen aránylanak egymáshoz. Tehát $AT_{1}T_{2}$ és $ADC$ háromszögekben az alapok aránya: ${c-a} \over {x-a}$. A területek aránya:
${({{c-a} \over {x-a}})^{2}}={{(c-a)(m_{1}+m_{2})} \over {(x-a)m_{1}}}$
Vagyis:
${{c-a} \over {x-a}}={{m_{1}+m_{2}} \over m_{1}}={1+{m_{2} \over m_{1}}}$
Innen:
${m_{2} \over m_{1}}={{c-a} \over {x-a}}-1={{c-a} \over {x-a}}-{{x-a} \over {x-a}}={{c-x} \over {x-a}}$
Megvan a magasságok aránya, írjuk fel a két kisebb trapéz területének arányát is:
${{m_{1}({{a+x} \over 2})} \over {m_{2}({{x+c} \over 2})}}={{{a+x} \over {x+c}}\cdot {m_{1} \over m_{2}}}={{{a+x} \over {x+c}}\cdot {{x-a} \over {c-x}}}={{x^{2}-a^{2}} \over {c^{2}-x^{2}}}$
Azt állítjuk, hogy a két terület egyenlő lesz, ez pedig úgy következik be, ha arányuk 1. Ekkor:
${{x^{2}-a^{2}} \over {c^{2}-x^{2}}}=1$
${{x^{2}-a^{2}}={c^{2}-x^{2}}}$
${{x^{2}+x^{2}}={a^{2}+c^{2}}}$
${2x^{2}={a^{2}+c^{2}}}$
${x={\sqrt {{a^{2}+c^{2}} \over 2}}}$
Vagyis ha a két trapéz területe egyenlő, vagyis két egyenlő területű trapézra vágtuk, akkor a szakasz hossza: ${x={\sqrt {{a^{2}+c^{2}} \over 2}}}$.

Mértani közép

Ha a trapézt két hasonló trapézra vágjuk, akkor annak a szakasznak a hossza, mellyel elvágtuk, a trapézon belül a két alap mértani közepe hosszúságú.
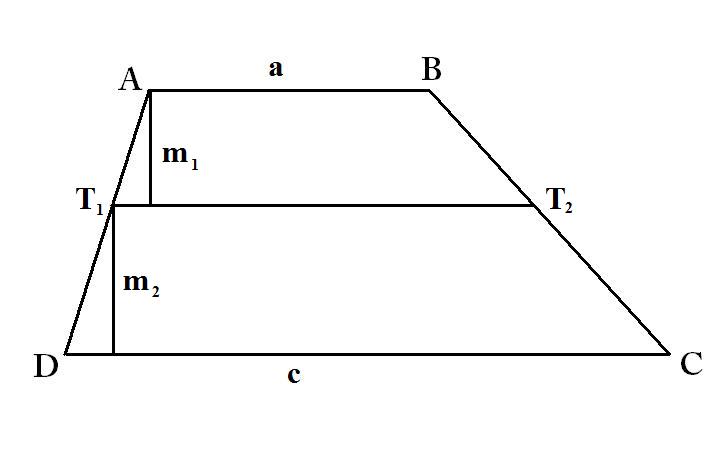
Az ábrán: $x={\sqrt {ac}}$

Bizonyítás

Két négyszög akkor hasonló, ha megfelelő szögeik egyenlő nagyságúak, valamint a megfelelő oldalainak aránya is megegyezik. Két trapéz akkor hasonló, ha a megfelelő szögeik egyenlőek, valamint az alapjainak és magasságainak aránya megegyezik. Ha $x={\sqrt {ac}}$, akkor $x^{2}=ac$.
$x\cdot x=a\cdot c$
${a \over x}={x \over c}={\sqrt {a \over c}}$ Tehát a két kisebb trapéz alapjainak aránya ${\sqrt {ac}}$. A magasságok aránya: ${m_{1} \over m_{2}}={{x-a} \over {c-x}}={\sqrt {a \over c}}$. (x helyébe beírtuk a ${\sqrt {ac}}$-t) Tehát a két trapéz alapjainak és magasságainak aránya megegyezik, méghozzá szögeik is egyenlőek a trapéz tulajdonságainak köszönhetően. Ekkor a területek aránya: ${{m_{1}({{a+x} \over 2})} \over {m_{2}({{x+c} \over 2})}}={{x^{2}-a^{2}} \over {c^{2}-x^{2}}}$ (az előző bizonyításból). Vagyis $x^{2}$ helyébe beírva $ac$-t: ${{ac-a^{2}} \over {c^{2}-ac}}={{a(c-a)} \over {c(c-a)}}={a \over c}$ Így biztosan kijelenthetjük, hogy ha két hasonló trapézra vágtuk az eredetit, akkor a szakasz hossza ${\sqrt {ac}}$.

A közepek közötti összefüggések vizuálisan (kör)

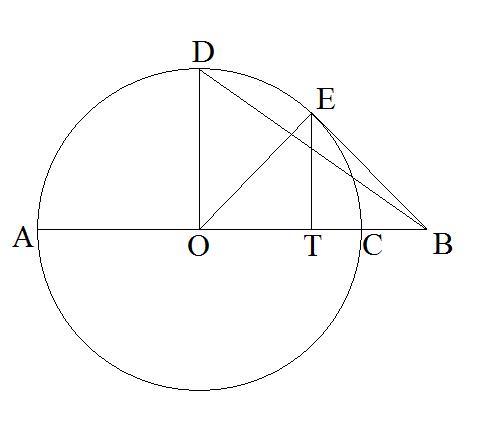
Az ábra magyarázata: $AC$ felezőpontja $O$, ami az $AC$ átmérőjű kör középpontja. $D$ az $O$-ba állított merőleges és a kör metszéspontja. $BE$ a kör érintője, ahol $E$ az érintési pont. $E$-ből a $AB$ egyenesre állított merőleges talppontja $T$.
Az ábrán szintén megjelennek a közepek, a következőképp: Ha $AB$ szakasz hossza $a$, illetve $BC$ szakaszé $b$, akkor $BT$ szakasz hossza $a$ és $b$ harmonikus közepe, $BE$ szakasz hossza $a$ és $b$ mértani közepe, $OB$ szakasz $a$ és $b$ számtani közepe és $BD$ $a$ és $b$ négyzetes közepe.
$BT={\frac {1}{\frac {{\frac {1}{a}}+{\frac {1}{b}}}{2}}}={2ab \over a+b}$
$BE={\sqrt {ab}}$
$OB={{a+b} \over 2}$
$BD={\sqrt {{a^{2}+b^{2}} \over 2}}$

Bizonyítás

• $BE$-ről könnyen belátható, hogy ${\sqrt {ab}}$ hosszú, hisz a $B$ pont körre vonatkoztatott hatványa alapján $a\cdot b=BE\cdot BE$. Innen $BE={\sqrt {ab}}$.
• $OB$ hosszát kiszámíthatjuk az $OC$ és $CB$ összegeként. $OB=OC+CB={{a-b} \over 2}+b={{a+b} \over 2}$
• $BD$ hosszát könnyedén kiszámíthatjuk Az $OBD$ háromszögben a Pitagorasz-tétel segítségével. $DB^{2}=OD^{2}+OB^{2}$, vagyis $DB={\sqrt {OD^{2}+OB^{2}}}={\sqrt {({{a+b} \over 2})^{2}+({{a-b} \over 2})^{2}}}={\sqrt {{a^{2}+b^{2}} \over 2}}$
• $BT$ hossza a $BTE$ háromszögből Befogótétellel kiszámítható. A tétel szerint $EB={\sqrt {OB\cdot TB}}$. Innen $TB={{EB^{2}} \over {OB}}={{ab} \over {{a+b} \over 2}}={{2ab} \over {a+b}}$

Kapcsolódó szócikkek

• Számtani és mértani közép közötti egyenlőtlenség
• Számtani és négyzetes közép közötti egyenlőtlenség
• Mértani és harmonikus közép közötti egyenlőtlenség

Források

• Definíciók
• Geometriai szemléltetés (kör)