Lineáris burok

Egy $a$ vektor és lineáris burka, $\operatorname {span} (a)$

A lineáris algebrában egy vektortér részhalmazának lineáris burka, más néven lineáris lezártja, generált vektortere azokból a vektorokból áll, amelyek előállnak a részhalmaz elemeinek, mint vektoroknak lineáris kombinációjaként, a vektortér alaptestének elemeivel, mint együtthatókkal. A lineáris burok altér, mégpedig a legkisebb altér, ami a halmaz minden elemét tartalmazza.

Definíció

A kék sík a $v_{1}$ és $v_{2}$ veltorok lineáris burka. ($v$ a két vektor lineáris kombinációja)

Konstruktív definíció

Legyen $V$ vektortér a $K$ test fölött, és $A\subset V$ részhalmaza a $V$ vektortérnek! Ekkor $A$ lineáris burka:

$\langle A\rangle =\left\{\left.\textstyle \sum \limits _{i=1}^{n}\lambda _{i}a_{i}\right|\lambda _{i}\in K,a_{i}\in A,n\in \mathbb {N} \right\}$

A lineáris burok $a_{i}$ elemeinek összes lineáris kombinációja.

Ha $A$ véges, akkor a definíció a következőre egyszerűsödik:

$\langle \{a_{1},a_{2},\dotsc ,a_{n}\}\rangle =\{\lambda _{1}a_{1}+\lambda _{2}a_{2}+\dotsb +\lambda _{n}a_{n}\mid \lambda _{1},\lambda _{2},\dotsc ,\lambda _{n}\in K\}$.

Az üres halmaz lineáris burka a nullvektortér, vagyis

$\operatorname {span} (\emptyset )=\{0\}$,

mivel vektorok üres összege definíció szerint a nullvektor.

További definíciók

A konstruktív definícióval ekvivalens definíciók:

• Egy $V$ vektortér $A$ részhalmazának lineáris burka a legkisebb vektortér, ami tartalmazza az $A$ halmazt
• Egy $V$ vektortér $A$ részhalmazának lineáris burka az a vektortér, ami előáll az $A$ halmazt tartalmazó alterek metszeteként

Jelölés

Egy $A$ halmaz lineáris burkának jelölése $\operatorname {span} (A)$, vagy $\operatorname {span} {[a_{1},a_{2},\dots ,a_{n}]}$, ha $A$ véges.

Tulajdonságok

Legyenek $A$ és $B$ részhalmazok a $K$ test fölötti $V$ vektortérben; ekkor:

• $A\subseteq \operatorname {span} (A)$
• $A\subseteq B\Rightarrow \operatorname {span} (A)\subseteq \operatorname {span} (B)$
• $\operatorname {span} (A)=\operatorname {span} (\operatorname {span} (A))$

Mivel ezek a tulajdonságok teljesülnek, azért a lineáris burokképzés burokoperátor.

Teljesülnek továbbá:

• Egy $V$ vektortér részhalmazának lineáris burka altere $V$-nek
• Egy $V$ vektortér $U$ alterének lineáris burka $U$
• Vektorok egy halmaza lineáris burkának generátorrendszere. Ha vektorok egy halmaza generál egy alteret, akkor a vektorhalmaz lineáris burka az altér.
• Két altér, $U_{1},U_{2}$ összege, $U_{1}+U_{2}=\{u_{1}+u_{2}\mid u_{1}\in U_{1},u_{2}\in U_{2}\}$ uniójuk lineáris burka. Tehát $U_{1}+U_{2}=\operatorname {span} (U_{1}\cup U_{2})$
• Legyen egy vektortér altereinek halmaza $T$; ekkor bevezethető egy kétaritású művelet, ami veszi az operandusok uniójának lineáris burkát. Ennek a duális művelete a metszetképzés. Ezekkel a műveletekket $T$ háló.
• Ha $U,V$ ugyanannak a térnek az altere, akkor a lineáris burokra teljesül a dimenziótétel:

$\dim(U+V)+\dim(U\cap V)=\dim U+\dim V$.

Példák

• Egyetlen $a\in \mathbb {R} ^{2}\setminus \{(0,0)\}$ vektor $\operatorname {span} (a)$ lineáris burka egy origón áthaladó egyenes
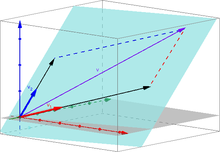
• A $(3,0,0)$ és a $(0,2,0)$ vektorok az $\mathbb {R} ^{3}$ vektortérnek. Lineáris burkuk $\operatorname {span} ((3,0,0),(0,2,0))$ éppen az $x$-$y$ sík.
• Legyen $K[[X]]=\left\{\left.\textstyle \sum \limits _{k=0}^{\infty }\lambda _{k}X^{k}\right|(\lambda _{k})_{k\in \mathbb {N} _{0}}\in K^{\mathbb {N} _{0}}\right\}$ a formális hatványsorok vektortere a $K$ test fölött, és legyen $A=\{X^{k}\mid k\in \mathbb {N} \}$ a monomok halmaza. Ekkor $A$ lineáris burka a polinomok halmaza:

  $\operatorname {span} (A)=\left\{\left.\textstyle \sum \limits _{i=0}^{n}\lambda _{i}X^{i}\right|n\in \mathbb {N} ,\lambda _{0},\dotsc ,\lambda _{n}\in K\right\}=K[X]$.

Forrás

• Gerd Fischer: Lineare Algebra. Eine Einführung für Studienanfänger (Grundkurs Mathematik). 17. Auflage, Vieweg+Teubner-Verlag, Wiesbaden 2010. ISBN 978-3-8348-0996-4, 384 Seiten.

Fordítás

Ez a szócikk részben vagy egészben a Lineare Hülle című német Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.