Carnot-ciklus
| Termodinamikai körfolyamatok |
|---|
A Carnot-ciklus (vagy Carnot-körfolyamat) egy speciális termodinamikai körfolyamat, melyet az elméleti (idealizált) Carnot-hőerőgép hajt végre. Ezt a fizikai modellt Nicolas Léonard Sadi Carnot javasolta 1824-ben, majd Émile Clapeyron dolgozta ki részletesebben az 1830-as és 1840-es években.
Egy termodinamikai rendszer állapotát állapotjelzők (nyomás, hőmérséklet, fajtérfogat, entalpia, entrópia) írják le. A termodinamikai körfolyamat akkor jön létre, ha a rendszer egy sor állapotváltozás után a kezdeti állapotába tér vissza. A körfolyamat végrehajtása során a rendszer munkát végezhet a környezetén, így hőerőgépként működhet. A hőerőgép működése során a környezetének egy melegebb régiójából energiát vihet át egy hidegebb régióba és az energia egy részét mechanikai munkává alakíthatja. A körfolyamat meg is fordítható. A rendszerbe külső munka bevezetése által hőenergiát képes átvinni egy hidegebb régióból egy melegebbe, ilymódon hőszivattyúként működhet.
A Carnot-körfolyamat a lehető legjobb hatásfokú körfolyamat, mely egy adott mennyiségű hőenergiát mechanikai munkává alakít, illetve egy adott mennyiségű mechanikai munkát hűtési célokra átalakít hőenergiává.
A Carnot-ciklus állapotváltozásai[szerkesztés]
A Carnot körfolyamat, ha hőerőgépként működik, négy állapotváltozásból áll:


- A gáz reverzibilis izoterm tágulása (expanziója) a TH[1] nagyobb hőmérsékleten (izoterm hőközlés). Ez alatt az állapotváltozás alatt (Az 1. ábrán A állapotból B állapotba) a táguló gáz munkát végez a dugattyún. A gáz tágulását a nagy hőmérsékletű tartályból beáramló hő okozza.
- Izentropikus (reverzibilis adiabatikus) tágulás. Ennél az állapotváltozásnál (B-ből C-be) feltesszük, hogy a henger és a dugattyú hőszigetelt: nem kap, és nem is veszít hőt a rendszer. A gáz tovább tágul, munkát végezve a környezetén. Ennek eredményeképp a gáz a hidegebb TC[2] hőmérsékletre hűl.
- Reverzibilis izotermikus összenyomódás (sűrítés, kompresszió) a TC hideg hőmérsékleten (izoterm hőleadás). (C-ből D-be). Ekkor a környezet végez munkát a gázon, miközben hő áramlik a gázból a hideg tartályba.
- A gáz izentropikus összenyomódása. (D-ből A-ba) Ismét feltételezzük, hogy a dugattyú és a henger hőszigetelt. A környezet végez munkát a gázon miközben összenyomja azt, ezáltal a hőmérsékletét TH-ra emelve. Az állapotváltozás végén a gáz a kiindulási állapotba jut vissza.
A hőmérséklet–entrópia diagram[szerkesztés]

A Carnot-erőgép vagy hűtőgép viselkedése jól szemléltethető a hőmérséklet–entrópia diagram (T–S diagram) segítségével. Ebben a közeg állapotát egy pont jelöli, melynek vízszintes koordinátája a fajlagos entrópia, függőleges koordinátája pedig a hőmérséklet. Egy termodinamikai folyamat (állapotváltozás), mely az A kezdeti állapotból a B végállapotba viszi át a közeget, a két pont közötti görbével ábrázolható. A görbe alatti terület az állapotváltozás alatt termelt (leadott) hőenergia:
Ha a folyamat a nagyobb entrópia irányába halad, a görbe alatti terület a rendszer által a környezetből felvett hővel egyenlő. Ha az állapotváltozás a kisebb entrópia felé halad, a görbe alatti terület a környezet felé leadott hő mennyisége lesz. Minden körfolyamatnál van a folyamatnak egy magasabb hőmérsékletű (felső) és egy alacsony hőmérsékletű (alsó) része. Ha a folyamat az óramutató járásával megegyezően halad, a felső terület a rendszerbe kívülről bevitt hőenergia, míg az alsó terület a rendszer által a környezet felé leadott hő lesz. A zárt görbén belüli terület, mely a két folyamat között helyezkedik el, a két hő különbsége, de mivel a belső energia a visszatérés után meg kell egyezzen a kezdeti értékkel, ez a különbség azzal a munkával egyenlő, melyet a folyamat egy ciklus alatt termel. Matematikailag kifejezve, reverzibilis folyamatokra a rendszer által egy körfolyamat alatt végzett munka így írható:
Mivel du teljes differenciál, integrálja minden zárt görbe mentén egyenlő nullával, ebből következik, hogy a T–S diagramon belüli zárt görbe területe egyenlő az óramutató járása szerint végrehajtott körfolyamat által szolgáltatott teljes munkájával, az óramutató járásával ellentétes irányban végrehajtott körfolyamatnál pedig a rendszerbe kívülről fektetett munkával.
Hatásfok[szerkesztés]

A fenti integrál kiszámítása a Carnot-körfolyamat esetén különösen egyszerű. A hőenergiából kinyert munka mennyisége:
A meleg tartályból a rendszerbe átáramló teljes hőenergia:
és a rendszerből a hideg tartályba átáramló teljes hőenergia:
- .
Az hatásfok:
ahol
- a rendszer által szolgáltatott munka (a rendszerből munka formájában kilépő energia),
- a rendszerbe belépő hő (a rendszerbe bevezetett hőenergia),
- a hideg tartály abszolút hőmérséklete és
- a meleg tartály abszolút hőmérséklete.
Ennek a hatásfoknak hőerőgép esetén a jelentése a meleg tartályból kivont hőenergiának a hasznos munkára fordított hányada. Hűtőgép körfolyamat esetében a hűtőgépbe bevezetett energiának és a meleg tartályból kivont energiának a viszonyát jelenti.
Carnot tétele[szerkesztés]
A diagramból kitűnik, hogy bármely körfolyamat hatásfoka, mely a és hőmérsékletek között zajlik le, nem haladhatja meg a Carnot-körfolyamat hatásfokát. Carnot tétele a következő: Egyetlen hőerőgép, mely két hőtartály között üzemel sem tud elérni jobb hatásfokot, mint az a Carnot-hőerőgép, mely ugyanezen két hőtartály között működik. Ilyen módon adott hőmérsékleti határok mellett a (3) egyenlet adja a lehető legjobb hatásfokot. Carnot tételének következménye, hogy az ugyanazon két hőtartály között működő reverzibilis hőerőgépek hatásfoka megegyezik. Átrendezve az egyenlet jobb oldalát könnyebben értelmezhető képletet kapunk. Nevezetesen, hogy egy hőerőgép elméletileg elérhető legnagyobb hatásfoka a meleg és hideg hőtartályok hőmérséklet-különbsége (az abszolút hőmérséklet kelvinben mérve egyenlő a Celsius-fokban megadott hőmérséklet plusz 273,15) osztva a meleg hőtartály hőmérsékletével:
- .
A fenti képletből érdekes következtetést lehet levonni. Ha a hideg tartály hőmérsékletét csökkentjük, azzal jobban lehet növelni a legnagyobb hatásfokot, mint a meleg tartály hőmérsékletének emelésével. Ennek elérése a gyakorlatban nehézségekbe ütközik, mivel a hideg tartály hőmérséklete az esetek többségében egyszerűen az adott környezeti hőmérséklet.
Valóságos hőerőgépek hatásfoka[szerkesztés]
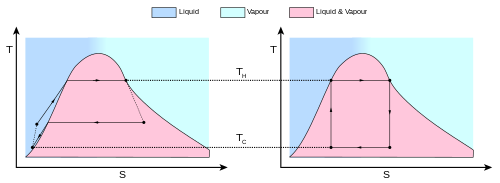
Carnot tudatában volt annak, hogy a valóságban lehetetlen reverzibilis hőerőgépet készíteni, ezért a valóságos hőerőgépek hatásfoka rosszabb, mint a (3) egyenlet értéke. Mindazonáltal a (3) egyenlet kiválóan alkalmas arra, hogy kiszámítsuk az adott hőfokhatárok között elérhető legjobb elméleti hatásfokot.
Bár a Carnot-körfolyamat mindössze csak elméletben létezik, Carnot hatásfok-képlete ettől még hasznos. Számítsuk ki a hőbevezetés és hőelvonás átlagos hőmérsékletét:
Helyettesítsünk a (3) egyenletbe TH és TC helyett <TH>-t, illetve <TC>-t. A Carnot-körfolyamatnál <TH> a legmagasabb és <TC> a legalacsonyabb elérhető hőmérséklet. Rosszabb hatásfokú rendszerek esetén <TH> kisebb lesz, mint TH és <TC> nagyobb lesz, mint TC. Ez jól szemlélteti, hogy a gőz újrahevítése vagy a tápvízelőmelegítés miért javítja a hatásfokot.
Jegyzetek[szerkesztés]
Irodalom[szerkesztés]
- Pattantyús Gépész- és Villamosmérnökök Kézikönyve 2. kötet. Műszaki Könyvkiadó, Budapest, 1961.















