Harmonikus rezgőmozgás

Harmonikus rezgőmozgás

A két szélsőérték között, szinuszos periodicitással végzett mozgást harmonikus rezgőmozgásnak nevezzük. Szemléletesen, ha egy rugóhoz rögzített testet kitérítünk nyugalmi helyzetéből és magára hagyjuk, a test két a szélső helyzet között periodikusan ismétlődő mozgást végez majd. (Itt a testet pontszerűnek tekintjük, és csak kis mértékben térítjük ki nyugalmi helyzetéből, így nem okozunk maradandó alakváltozást a rugóban. A mozgás leírása során a külső erők hatását (pl. közegellenállás) elhanyagoljuk.)

Vannak nem-harmonikus rezgőmozgások is, ezek közül legfontosabbak a csillapított rezgések.

A mozgás jellemzése

Harmonikus rezgőmozgás

• A test nyugalmi helyzettől való legnagyobb kitérését amplitúdónak nevezzük. Jele: A, mértékegysége: m (méter).
• A periódusidő vagy rezgésidő az egy teljes rezgés megtételéhez szükséges idő. Jele: T, mértékegysége: s (másodperc).
• A rezgésszám a t idő alatt megtett rezgések száma, jele: N, mértékegység nélküli mennyiség.
• A rezgés frekvencia az időegység alatt megtett rezgések száma. Jele: f vagy $\nu$, mértékegysége: $\frac{1}{s}=Hz$ (hertz). $f=\frac{1}{T}=\frac{N}{t}$
• A körfrekvencia jele: $\omega$, mértékegysége: rad/s (nem összetévesztendő a rezgés frekvenciával, melynek mértékegysége 1/s = Hz). $\omega=\frac{2\pi}{T}=2\pi f$
• A kezdőfázis jele: $\phi_0$, mértékegység nélküli mennyiség.

Kinematikai leírás

Kitérés-idő grafikon

Kitérés, sebesség, gyorsulás

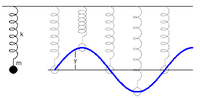
Kitérés-idő függvény: $x(t)=A\cdot\sin(\omega t+\varphi_0)$
Sebesség-idő függvény: $v(t)=A\omega\cdot\cos(\omega t+\varphi_0)$
Gyorsulás-idő függvény: $a(t)=-A\omega^2\cdot\sin(\omega t+\varphi_0)=-\omega^2x$

A harmonikus rezgőmozgást végző test gyorsulása egyenesen arányos a kitéréssel, és azzal ellentétes irányú. A sebesség és a gyorsulás is periodikus függvénye az időnek.

A sebesség maximuma a sebességamplitúdó: $v_{max}=A\omega$
A gyorsulás maximuma a gyorsulásamplitúdó: $a_{max}=-A\omega^2$

Az egyenletes körmozgás és a harmonikus rezgőmozgás kapcsolata

Figyeljünk meg egy egyenletes körmozgást és egy harmonikus rezgőmozgást végző tömegpontot! A körmozgást állítsuk be úgy, hogy a sugara egyezzen a rezgés amplitúdójával, és periódusidejük megegyezzen. Ha oldalról (a körmozgás síkjából) egymás mellé vetítjük a két tömegpont árnyékát, azonos kezdőfázis esetén a két árnyék együtt mozog, mindkettő harmonikus rezgőmozgást végez.

Harmonikus rezgőmozgás referenciaköre

Egyenletes körmozgás és harmonikus rezgőmozgás

Dinamikai leírás

A harmonikus rezgőmozgást a pont egyensúlyi helyzetétől mért kitérésével egyenesen arányos, és azzal ellentétes irányú erő, az úgynevezett harmonikus erő hozza létre: $F=-Dx$, ahol D rugóállandó vagy direkciós állandó.

A dinamika alapegyenlete: $m\ddot{x}=-Dx$.

A differenciálegyenlet megoldásaként olyan függvényt keresünk, melynek idő szerinti második deriváltja arányos magával a függvénnyel. Ilyen pl. a szinusz és a koszinusz függvény.

Az egyenlet megoldása: $x(t)= A\cdot\sin(\omega t+\varphi)$, ahol a körfrekvencia $\omega=\sqrt{\frac{D}{m}}$, a periódusidő $T=2\pi\sqrt{\frac{m}{D}}$.

Rezgések összetétele

Egyirányú, azonos frekvenciájú rezgések összetétele

A két rezgés frekvenciája megegyezik, amplitúdójuk és kezdőfázisuk eltérhet. A két rezgés kitérés-idő függvénye:

$x_1(t)=A_1\cdot\sin(\omega t+\varphi_1)$
$x_2(t)=A_2\cdot\sin(\omega t+\varphi_2)$

Az eredő mozgás kitérés-idő függvénye: $x(t)=A_1\cdot\sin(\omega t+\varphi_1)+A_2\cdot\sin(\omega t+\varphi_2)=A\cdot\sin(\omega t+\delta)$,

ahol az amplitúdó $A=\sqrt{A_1^2+A_2^2+2A_1A_2\cos(\varphi_2-\varphi_1)}$ és a kezdőfázis $\tan\delta=\frac{A_1\sin\varphi_1+A_2\sin\varphi_2}{A_1\cos\varphi_1+A_2\cos\varphi_2}$.

Speciális esetek

• Maximális erősítés

  Amikor $\varphi_1=\varphi_2$, vagyis a rezgések azonos fázisúak, akkor $A=A_1+A_2$, azaz az eredő rezgés amplitúdója az összetevő rezgések amplitúdójának összege.

• Maximális gyengítés

  Amikor $|\varphi_2-\varphi_1|=\pi$, vagyis a rezgések ellentétes fázisúak, akkor $A=|A_1-A_2|$, azaz az eredő rezgés amplitúdója az összetevő rezgések amplitúdójának különbsége. Ha az ellentétes fázisú rezgések amplitúdója megegyezik, A=0, a két rezgés kioltja egymást.

Egyirányú, különböző frekvenciájú rezgések összetétele

A két rezgés frekvenciája különbözik, amplitúdójuk és kezdőfázisuk eltérhet. Egy egyszerűsített esetet vizsgálunk, amikor az amplitúdók és a kezdőfázsok megegyeznek. A két rezgés kitérés-idő függvénye:

$x_1(t)=A\cdot\sin(\omega_1 t)$
$x_2(t)=A\cdot\sin(\omega_2 t)$

Az eredő mozgás kitérés-idő függvénye: $x(t)=A\cdot\sin(\omega_1 t)+A\cdot\sin(\omega_2 t)=2A\cdot\cos(\frac{\omega_1-\omega_2}{2}t)\sin(\frac{\omega_1+\omega_2}{2}t)$.

Az amplitúdó $A^*=2A\cdot\cos(\frac{\omega_1-\omega_2}{2}t)$.

Az amplitúdó az idő függvényében periodikusan változik, ezt lebegésnek nevezzük.

Eredő pályák A=B esetén

Merőleges, azonos frekvenciájú rezgések összetétele

A két rezgés frekvenciája megegyezik, amplitúdójuk és kezdőfázisuk eltérhet. A két rezgés kitérés-idő függvénye:

$x(t)=A\cdot\sin(\omega t)$
$y(t)=B\cdot\sin(\omega t+ \delta)$

Az eredő mozgás pályája: $\frac{x^2}{A^2}+\frac{y^2}{B^2}-2\frac{xy}{AB}\cos\delta=\sin^2\delta$. Ez egy ellipszis egyenlete.

Az ellipszis tengelyének iránya $\delta$ fáziskülönbségtől függ.

Merőleges, különböző frekvenciájú rezgések összetétele

A két rezgés frekvenciája különbözik, amplitúdójuk és kezdőfázisuk eltérhet. A körfrekvenciák aránya ($\omega_1:\omega_2$) alapján két esetet különböztetünk meg:

• Ha a két körfrekvencia aránya racionális, az eredő rezgés periodikus és a pálya zárt. Ezeket a görbéket Lissajous-görbéknek nevezzük.

1:2

1:3

1:6

2:3

3:4

3:20

17:23

97:101

• Irracionális arányú körfrekvenciák esetén a pályagörbe nem záródik.

Lásd még

• Fizikai inga
• Matematikai inga
• Rezgés
• Rezonancia

Források

• Budó Ágoston: Kísérleti fizika I.
  Tankönyvkiadó, Budapest
• Tasnádi Péter - Skrapits Lajos - Bérces György: Mechanika I.
  Dialóg Campus Kiadó, Budapest-Pécs ISBN 963-9310-23-9

Külső hivatkozások

• Fizikai kísérletek gyűjteménye: Harmonikus rezgés
• Qliss3D - Lissajous-görbe rajzoló program (Ubuntu)